宽角抛物方程模型处理复杂地形的一种方法*

2019-05-31俞红兵胡绘斌储飞黄

通信技术 2019年3期

俞红兵，胡绘斌，储飞黄

（1.国防科技大学电子对抗学院，安徽合肥 230037；2.94860部队，江苏南京 210018）

0 引言

在现代电子战中，根据战场环境的实际数据准确分析和评估复杂地形环境对电波传播和电子战系统作战性能的影响，对于辅助指挥员进行正确的战术部署和选择恰当的战略战术，以获取战场电磁优势、掌握战场制电磁权具有极其重要的意义。迄今为止，人们已经建立了多种计算复杂地形上电波传播特性的数学模型，其中，抛物方程模型（Parabolic Equation Model，PEM）是一种基于Maxwell方程建立起来的确定性电波传播模型，与几何光学(GO)或物理光学（PO）模型相比，其计算过程简单且精度高，与矩量法（MOM）、有限元法（FEM）等积分方程方法和时域有限差分法（FDTD）等微分方程方法相比，PEM对内存要求低、计算速度快，可以进行远距离电波传播特性预测。由于上述优点，近年来，PEM得到了人们广泛的关注和研究[1］。

和求解任何形式的Maxwell方程组都需要初始条件和边界条件一样，用PEM计算电波传播问题时，主要需解决三个问题：（1）如何确定PEM的初始值？（2）采用何种数值方法求解抛物方程（PE）？（3）在相应的数值求解方法中，如何处理PE的边界条件？对前两个问题，前人已进行过比较深入的研究[2-3］，在此不再赘述，本文主要探讨第（3）个问题——PEM处理复杂地形边界条件的方法。为此，首先介绍计算电波传播特性的PEM。

1 PEM概述

二维波动方程通过一定的近似处理可以转化为以下的Feit-Fleck型二维宽角PE[2］：

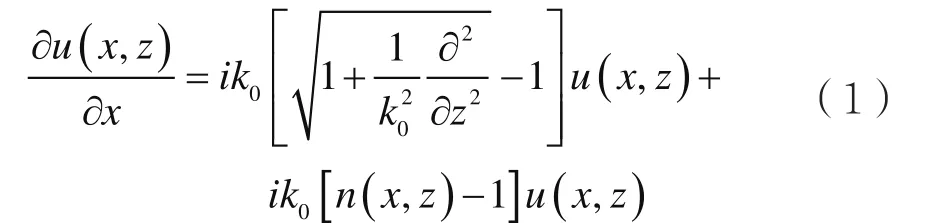
式中，u(x,z)为任意距离-高度点上的场分布，n(x,z)=n0(x,z)+z/Re为随地形高度变化而修正的大气折射指数。n0为发射天线所在高度处的大气折射指数，x、z分别表示传播距离和高度，Re≈6370 km为地球半径，k0=2π/λ为自由空间传播常数。

式（1）就是宽角PEM。根据收发点之间的地形高程数据（可通过数字地图来获得）和地表电磁特性（主要为介电常数εr和电导率σ，可按ITU_R 527-4的规定来确定或人为确定[4］），结合收发点之间路径上的大气折射指数n(x,z)分布（对于低于1 km的低层大气可通过已有成熟模型计算获得[5］），采用离散分步混合付立叶变换方法（DMFT）来数值求解1)式[3,6］，就可计算出收发点之间的电波传播路径衰减。本文主要阐述PEM处理由地形高程数据描述的不规则地形边界的方法和步骤。

2 PEM处理复杂地形边界的方法

复杂地形环境主要指电波传播区域的地势是高低起伏的，地表特征则表现为海水、淡水、干燥地、湿地等类型[4］。

为了能够采用DMFT来求解PE，需将不规则地形上的PE转换成平地面上PE的形式，为此，需对图1所示的不规则地表进行坐标变换。

图1 不规则地表的平地面转换

以函数z=T(x)=t(x)-x2/(2Re)来描述不规则地表，其中，t(x)为描述地形起伏边界的函数，x2/(2Re)项则是考虑了地球曲率的影响。以不规则地形上某一点作为坐标原点，建立一个新坐标系(x´,z´)，且满足：

设u(x,z)=e-iθψ(x,z)，θ为待定变量，ψ(x,z)为任一标量场分量，根据图1，将式（2）代入式（1），可以得到以下形式的宽角PE[3］：

为了使式（3）与式（1）形式相同，设

将式（4）、式（5）代入到式（3）中可得：

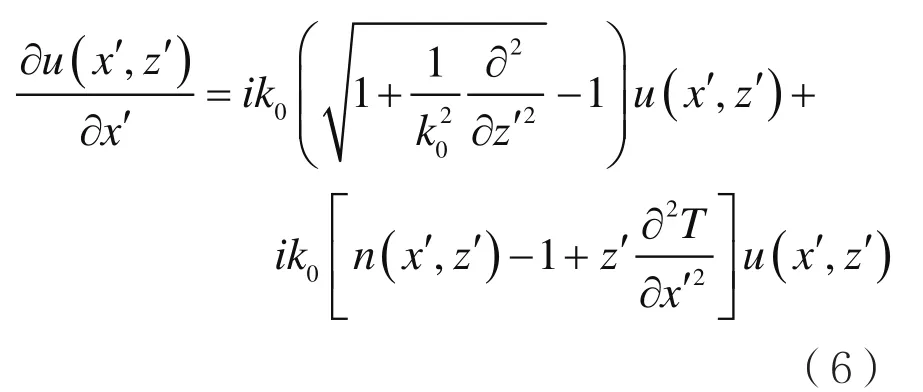
这就是经平地面地形变换后所导出的宽角PE模型，通常将包含n(x´,z´)的项以修正折射指数表示为：

式（6）和式（1）相比仅仅是折射指数项不同。在式（7）中，若∂T2/∂x´2=0（即平地面），则m(x´,z´)=n(x´,z´)-1，这时式（6）就与式（1）完全一致。可见，通过平地面转换，不规则地形对宽角PE的影响完全转换为平地面上对大气折射指数分布的影响。

当从数字地图中抽取传播地形剖面数据时，这种离散数据使得地形剖面是分段线性的，只存在∂T/∂x´项，∂T2/∂x´2=0，式（6）符合平地面条件，可采用DMFT求解。以下本文将详细阐述对分段线性地形的处理方法。

为简单起见，将 ∂2T/∂x´2用二阶中心差分的形式来代替，即

假设地形剖面上A、B两段是不连续的，其斜率分别为TA´和TB´，且TA´≠TB´，A、B两段地形上方的场分别以ψA和ψB表示，如图2所示。

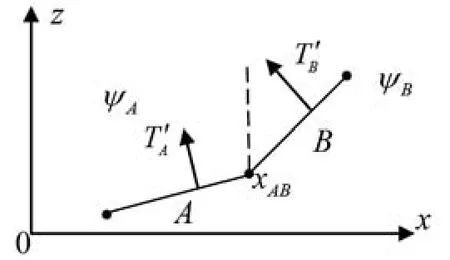
图2 地形剖面中不连续的两段斜面

由于A、B的斜率不同，在电磁波由A传播到B的过程中，根据式（4），在A、B段的交点xAB处θ是不连续的，而u(x,z)=e-iθψ(x,z)，因此ψA和ψB在相位上也是不连续的。为了反映地形变化对电磁场相位的影响，本文设定：

式（9）的思想就是当电磁波由A传播到B时，根据两段地形斜率强行改变B段上方场的相位，这与McArthur和Bebbington提出的扭转波阵面的思想[7］十分相近。

在计算地表以上各高度网格上的场分布时，对于平地面边界的情况，可采用DMFT方法计算出任意步进上、从0至zmax高度范围内的场分布。对于不规则地形，各高度网格上场的计算也都要从地表算起，但此时地表高度不一定为零，因此对于分段线性地形剖面，除了要计算不连续地形交界点处的场以外，还需要将不同的地表高度转换为相对零高度来计算。为此，本文采用所谓的“边界平移法”（Boundary Shift，BS）来进行这样的转换处理，具体如下。

如图3所示，设电波传播到某一距离点D1处，其地表上方波阵面上的场为u(x,iΔz)，i=1,2,…N，N为DMFT算法的尺度。经过一个步进后，波阵面传播到D2，设D2与D1处地表的高度差为Tx，则Tx所包含的高度网格数为

显然，Tx-NtΔz＜Δz。

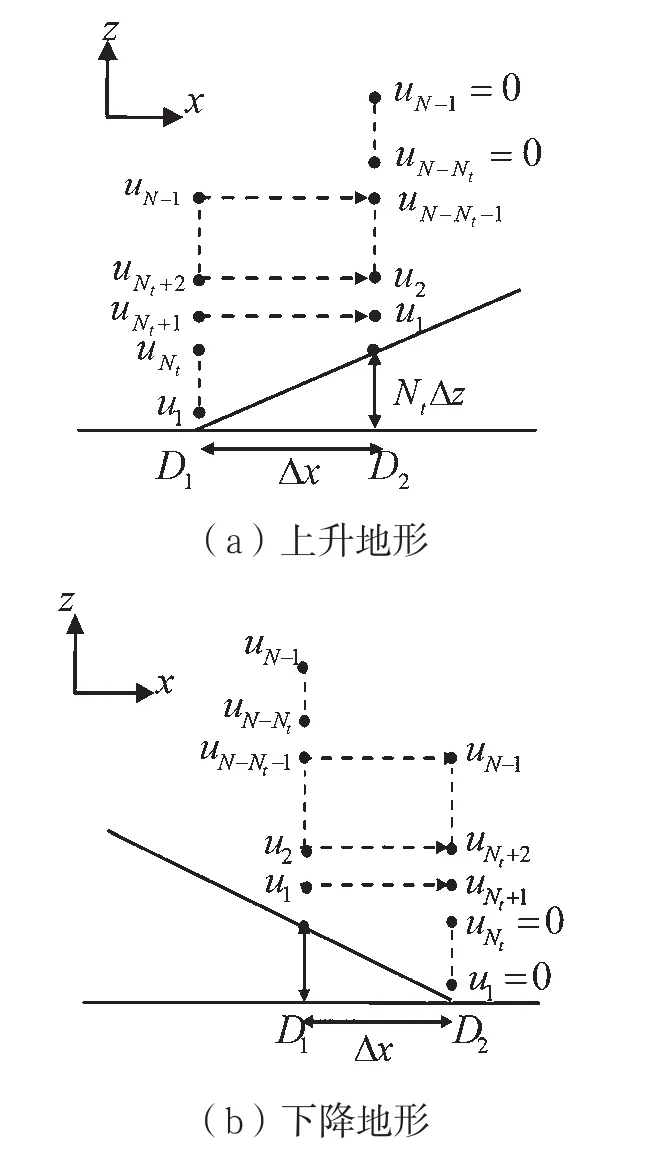
图3 边界平移（BS）法示意图

在用BS方法计算D2处的场分布时，如果D2处是上升地形，即Tx＞0，则首先由D1处的场分布计算出D2处的场分布，再将此场分布的网格序号往下平移Nt这样，D2处最大高度上所对应的网格序号就由N-1下降为N-Nt-1，再将超出最大高度的第(N-Nt)～(N-1)个网格点上的场设为零，就得到D2处从地表起至最大高度处各网格上的场分布，即

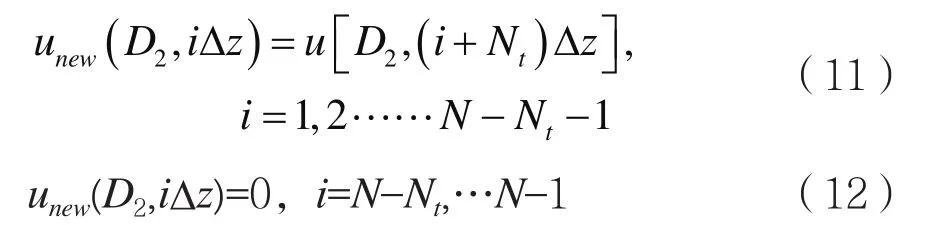
如图3（a）所示。显然，此时D2处的u所包含的元素个数还是N-1。

如果D2处是下降地形，即Tx＜0，同样地，将D2处场分布的序号往上平移Nt，同时，不高于NtΔz的各高度网格点上的场也设为零，即：

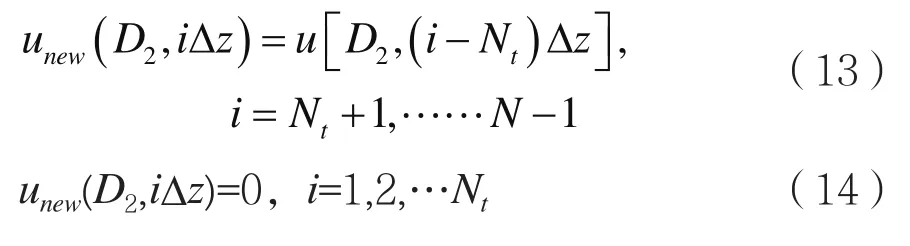
如图3（b）所示。显然，此时D2处的u所包含的元素个数也还是N-1。

如果D2和D1高度相同，即Tx=0，则维持原来波阵面上的场分布，不进行BS转换。

通过以上的BS方法处理，在计算仰角范围内，式（6）就可以计算不规则地形上任意距离和高度处的场分布。例如，要计算距离为D、高度为H的p点处的场值，如图4所示，图中以▲表示p点所处的位置。

图4 不同高度、不同距离点处场的计算方法

当p点恰好位于高度网格上，即mod(H/Δz)=0时，mod表示取余数计算，则第H/Δz网格上的场即为所求；当p点不位于任何高度网格上时，mod(H/Δz)≠0，此时可以通过对p点上下两个网格点上的场进行插值计算来获得p点的场值。不妨设

则采用线性内插方法时，p点的场为：

当距离点D恰好位于某个步进处时，该步进上的u即为D处的场分布，当D不位于任何一个步进上时，同样可以采用线性内插的方法求得D处的场分布，即

如图（4）所示。

至此，利用DMFT算法[6］，结合上述对不规则地形的处理方法，就可以用式（6）的宽角PEM计算不规则地形条件下任意距离和高度点处的电波传播衰减。

3 算例

为了便于比较，本文采用文献[8］中的一个算例，同样不考虑自由空间电波传播损耗。

算例：标准大气条件下（即∂n/∂h≈-40×10-6时的大气环境），电波在一个类似正弦包络形状的不规则地形上传播，其中，地形函数为：

显然，这是一个∂2T/∂x2≠0的连续函数。式中，h=229 m为包络的最大高度，x1=15 km为包络半高程所在的距离，w=10 km为包络的半宽度。地形剖面如图5所示。

图5 类似正弦包络的地形剖面

发射天线高度为Ht=30.5 m，频率为f=3.0 GHz，高斯方向图：A(p)=e-p2ω2/4，p=k0sin(θ-θ0)，θ0为发射天线的仰角，θ为每一步进处的射线仰角，为方向图的3 dB宽度。电波水平极化。最大传播距离为rmax=50 km。所有地表均设为PEC。

图6（a）显示了本文计算结果的伪彩图，图中的不同颜色代表自地面起至600 m高度区域内的电波传播衰减值分布，其中，图下方的色带显示了不同衰减值所对应的颜色。

图6（a）和文献[8］中的图2基本上是一致的，主要的区别就是：在0～5 km距离范围内，在一些较高的点上，图6（a）没有给出衰减计算结果。这是因为这些点处的仰角超过了宽角PE模型的计算仰角，没有计算。文献[8］中的图2虽然显示了0～5 km距离内较大仰角处的衰减值，但不排除这是采用其它方法计算所得的结果。

图6（b）则显示了最大距离处电波传播衰减值随高度变化的情况。从图中可见，从地面起至地形最大高度处，传播区域逐渐由阴影区过渡到亮区，在200 m高度以上，由于天线的高度增益，衰减值几乎沿直线减小。总体来看，电波在类正弦地形上的传播衰减特性和在单刃峰地形上的绕射效应类似，只是其衰减值的振荡更大。

图6 电波在类正弦包络地形上的传播衰减

通过以上算例可以看出，本文方法计算不规则地形上的电波传播特性是比较准确的。由于算例中所有的地表都设为PEC，因此，在计算PE初始场时，地表反射系数取为-1。实际上，对于非PEC的地表结构，本文方法依然适用，只是需要根据地表的相对介电常数εr和电导率σ，计算出地表反射系数，再由反射系数计算出新的PE的初始场分布即可，地表类型并不影响本文对地表的处理方法。