基于靶板冲塞式破坏的战斗部破片优化设计*

余丽山，李彦彬，翟夕阳，金学科，何小九

(空军工程大学防空反导学院，西安 710051)

0 引言

目前地空导弹主要采用半预制或预制破片战斗部。它主要依靠大量高速飞行的破片来命中并击穿来袭目标的关键部件，或者引燃油箱、引爆弹药进而实现对敌武器的毁伤。破片杀伤战斗部对目标的杀伤效果，除了与目标易损性和交会条件相关，还显著与战斗部装药结构尤其是破片的初速和几何尺寸相关。选择合理几何尺寸的破片，并确定其抛撒速度，最大程度的发挥战斗部破片对目标的杀伤效果，同时保证导弹的机动性是地空导弹破片杀伤战斗部设计面临的难题之一。

针对导弹破片杀伤战斗部破片的设计问题，国内外主要采用理论分析、数值模拟和试验手段进行研究。Valerio Cozzani[1]对实际破片形状和数量进行等效优化分析，通过对舰船毁伤情况的评估来指导战斗部破片的设计；李旭峰[2]从战斗部的装药结构和材料的角度研究具有高效毁伤作用的含能破片设计方案，并通过实验验证设计的正确性；魏峰[3]采用数值模拟手段对球形破片在炸药爆炸驱动作用下的飞散特性进行了分析，基于仿真结果对战斗部破片进行了优化。文中针对地空导弹破片杀伤战斗部的优化设计问题，对破片飞散特性以及破片与薄靶作用行为进行了分析，基于破片能量消耗和比动能双重原则，建立了战斗部破片参数优化设计的双目标规划模型，并引入了遗传算法对模型进行求解，最后有效地得到了战斗部破片优化设计的各参数。

1 破片的运动分析

破片杀伤战斗部对目标进行毁伤作用主要是依靠产生的高速运动破片群。当战斗部内的炸药爆炸时，在一瞬间可产生数十万大气压以上的压力，由于战斗部壳体材料的屈服强度远远小于此压力，于是壳体破裂并产生高速运动的破片群，击穿、引燃或引爆目标[4]。

根据格尼公式，圆柱形壳体战斗部装药爆炸后，静态破片初速度为[5]:

(1)

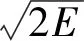
破片在飞行过程中，其运动方程为：

(2)

式中：mf和vf分别表示破片的质量和速度；cx表示阻力系数，取决于破片的形状以及飞行速度，文中假设cx为常数；ρa表示遭遇点的空气密度;Af表示破片的平均有效面积(迎风面积)。令衰减系数k=cxρaAf/(2mf)，则解得破片飞行到不同距离的存速：

vf=v0e-kx

(3)

当战斗部爆炸后形成破片静态初速度为v0时，破片在飞行过程中会受到空气阻力而导致速度衰减，速度衰减系数k与破片的形状、破片飞行的速度、空气密度、破片的迎风面积和质量有关。当破片的飞行距离为x时，破片的存速为vf。

2 破片对薄靶板目标的撞击和侵彻

由图1破片对薄靶板的侵彻模型可知，破片在穿孔时，在破片和目标靶板接触的地方，会形成蘑菇头效应，导致穿孔时孔径变大。

破片高速飞向目标靶板时，在破片和靶板接触的同时挤压目标靶板。由于高速运动破片的作用，使得在和靶板接触的截面上，产生剪应变和剪应力，并伴随着热量生成。瞬间产生的大量热量在短时间内来不及散去，导致接触部位温度迅速升高，从而降低了目标靶板的抗剪能力，产生了冲塞式破坏[6-7]。破片的动能主要转化为4部分：①剩余破片和击穿靶板后形成塞块的动能；②薄靶板被剪切时消耗的能量；③击穿薄靶板过程中破片损失质量的动能；④破片撞击薄靶板时由于变形所消耗的能量。根据文献[8]中的动量方程和能量方程解得破片的剩余速度为：

(4)

式中：m、mr分别表示为塞块的质量、破片的剩余质量；v50表示破片的弹道极限穿透速度，即破片以v50的速度撞击靶板刚好可以穿透。

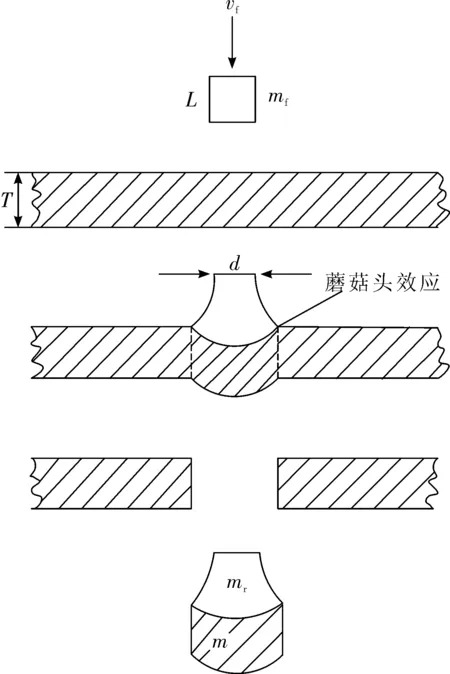
图1 破片对薄靶板的侵彻过程

塞块的质量为：

m=ρmAfTsecθ

(5)

式中：ρm为靶板的密度，kg/m3；Af为破片的横截面积，m2；T为靶板的厚度，m；θ为破片的入射角度，(°)。

破片贯穿靶板的极限速度为：

(6)

式中：d为侵彻体直径，m；L为侵彻体长度，m；C、K、b为经验常数，对于钢质破片侵彻钢靶，其值分别为1 297，-164，0.61，单位都是m/s。

破片的剩余质量为：

(7)

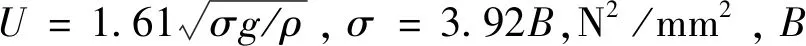
3 毁伤准则

破片杀伤战斗部爆炸后，形成大量高速运动、不同形状的破片。每个破片都相当于一个能量体，击穿并摧毁目标的致命性部件。从目标的角度考虑，可将致命性部件等效为目标靶板。确定毁伤准则时，既要从目标靶板的整体(破片能量消耗准则)考虑，又要从目标毁伤的局部(比动能准则)考虑。

3.1 破片能量消耗准则

从目标整体考虑，破片的能量消耗形成对目标靶板的毁伤。破片消耗的能量越多，对目标的毁伤程度越大。

破片消耗的能量为[9]：

(8)

3.2 破片比动能准则

战斗部破片在空气中飞行时除受到自身的重力外，还受到空气阻力。因此，在不断减速的同时也会旋转。从目标毁伤的局部考虑，破片与目标遭遇时接触面积对毁伤的效果也有较大的影响。

单位面积厚度靶板上所接受的比动能为[10]：

(9)

式中：S为破片与靶板的期望接触面积，S=km2/3，圆柱形状系数k=3.35×10-3m2·kg-2/3；h为靶板击穿处的侵彻厚度，h=T/cosθ。

破片对目标靶板进行贯穿损伤时，靶板在单次打击下的毁伤概率经验公式为：

(10)

4 算例验证

4.1 目标函数

战斗部破片的优化设计以考虑对目标的毁伤程度为基础。若对目标毁伤程度最大，应保证破片以消耗最大的能量撞击目标以及破片贯穿目标时对目标的毁伤概率最大，即：

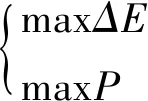
(11)

假设战斗部爆炸时，破片的形状为圆柱体，破片的初速度及结构参数在一定的区间内变化，即：

s.t.

(12)

对于双目标优化的问题，可以根据目标的重要性程度不同，将双目标转化为单目标优化。

当目标靶板上接受比动能Eb≥4.5时，靶板在破片打击下的毁伤概率如图2。

由图2可知，当目标的毁伤概率P≤95%时，随着比动能的增大，目标的毁伤概率迅速增加。但当P>95%时，尽管比动能大幅度增加，目标的毁伤概率增加的却并不明显。因此可以将ΔE作为主目标优化函数，将毁伤概率P经过处理后加入到主目标优化函数的约束条件中。具体处理方法：确定常数ξ(ξ的确定可根据对目标的期望毁伤概率)，令P≤ξ，v0∈[1 000 m/s，2 000 m/s]，d∈[0.7 cm，1.4 cm]；L∈[0.7 cm，1.4 cm]，求主目标函数ΔE的最大值。即：

maxΔE

s.t.

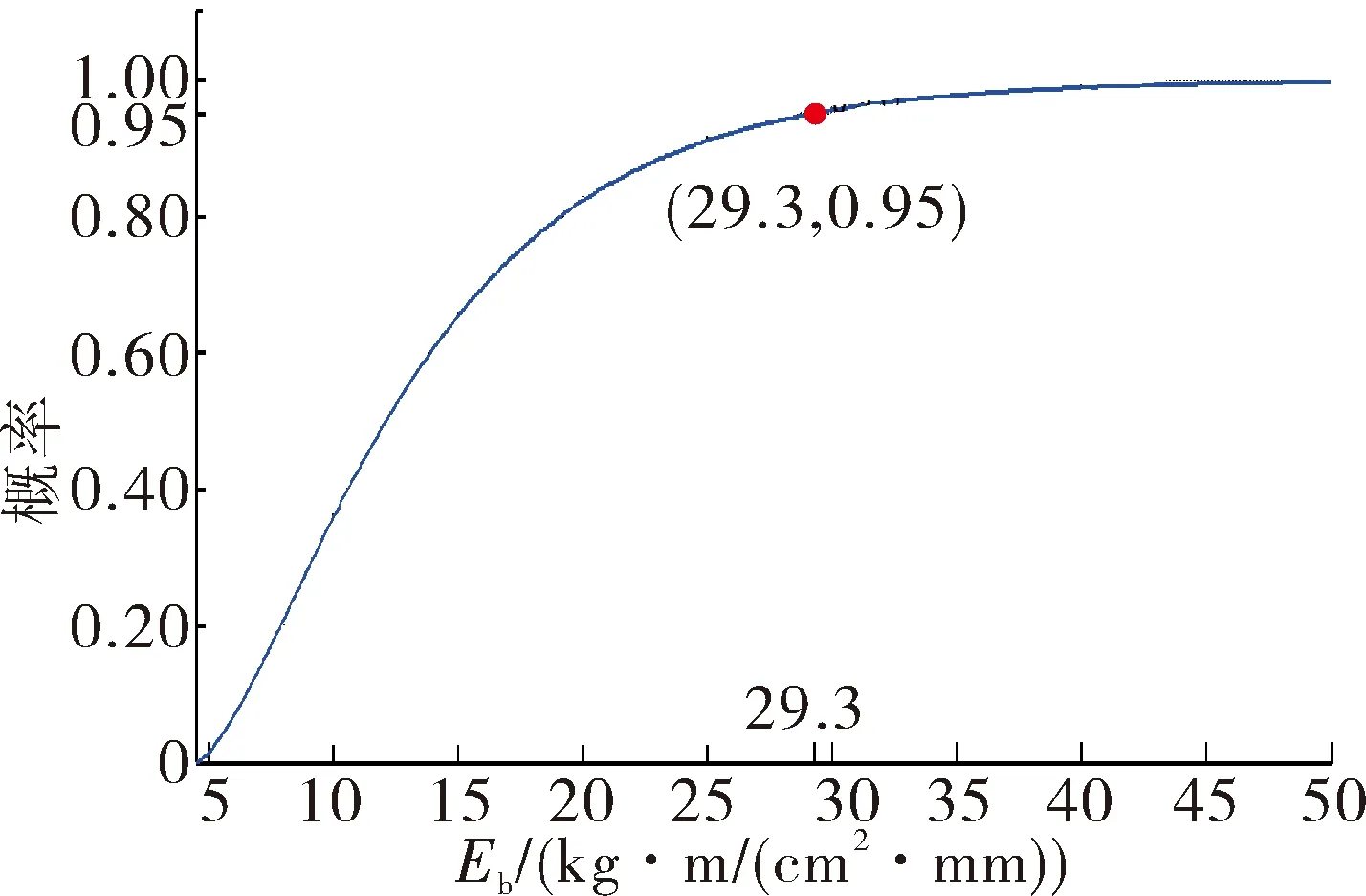
图2 毁伤概率曲线

4.2 遗传算法

遗传算法是根据生物界的自然选择以及遗传变异等机制，提出的一种具有全局性概率搜索能力的智能算法。它具有很高的智能性、很强的鲁棒性、较高的扩充性[11-13]。使用遗传算法可有效地对本案例求解。

遗传算法步骤为：

②在搜索空间U中随机产生10个个体，s1，s2，…，s10，置代数器t=1，初始种群S(1)={s1，s2，…，s10}。

③计算S中个体si的适应度函数fi=f(si)。

④确定算法停止条件，若满足，则算法终止，所求结果即为S中适应度最大的个体。否则，计算概率：

(13)

按照上述选择概率从S中随机选择1个染色体进行复制，共做10次得群体S1。

⑤从S1中按照交叉率Pc确定进行交叉的染色体c，配对进行交叉得群体S2。在群体S2中按照变异率Pm随机确定m个染色体，变异m次后得群体S3。

⑥将S3作为新一代种群，用S3替代S，t=t+1，转③。

流程图如图3所示。

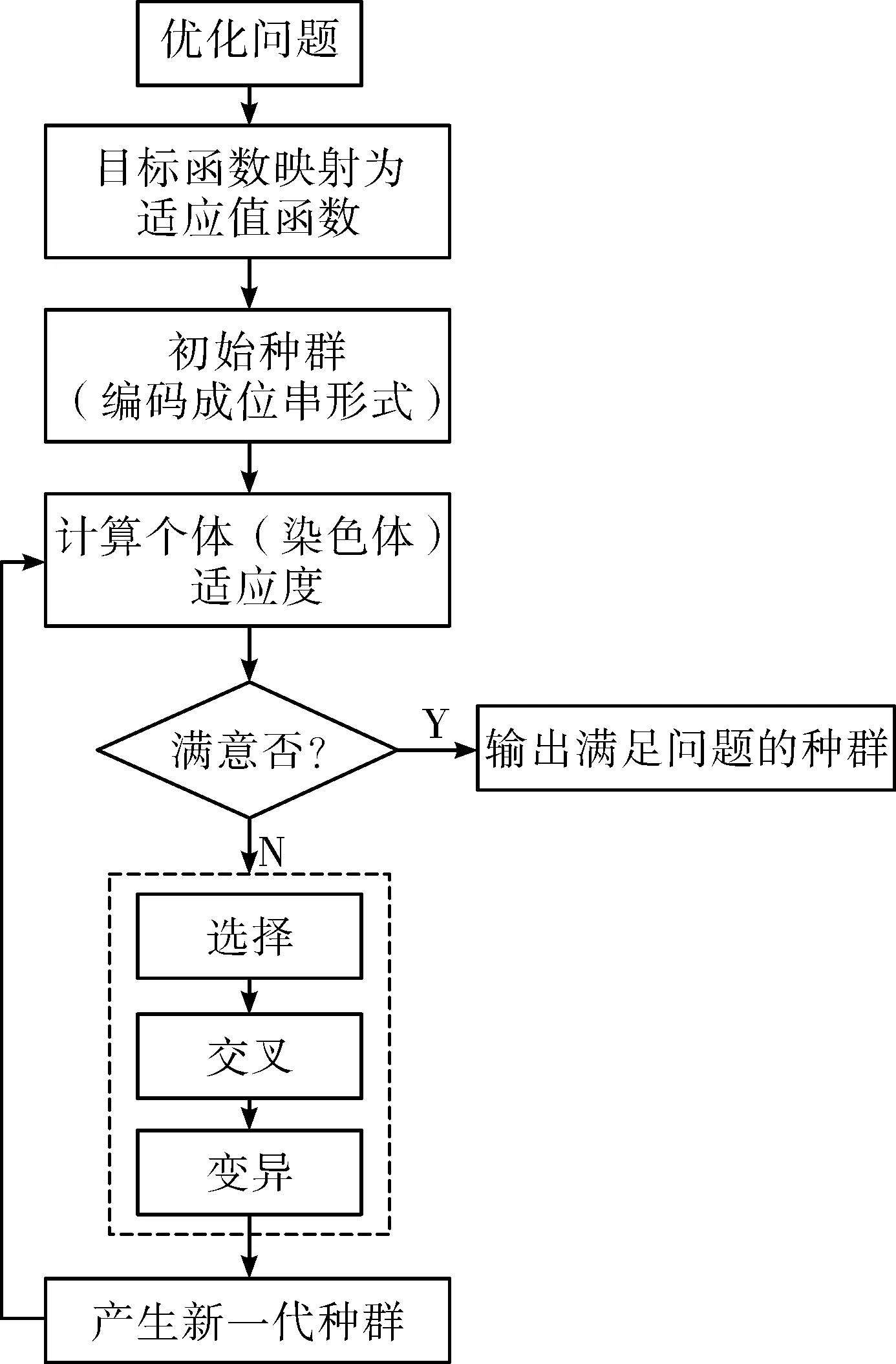
图3 遗传算法流程图

4.3 算例结果

假设钢质圆柱体破片在20 m处正对钢质目标靶板飞去，即破片的入射角度θ=0°，钢的密度ρ=7.85 g·cm-3，阻力系数cx=1.12，薄板的厚度为2 mm。得到破片撞击目标靶板消耗的能量随破片的各参数变化迭代次数如图4。

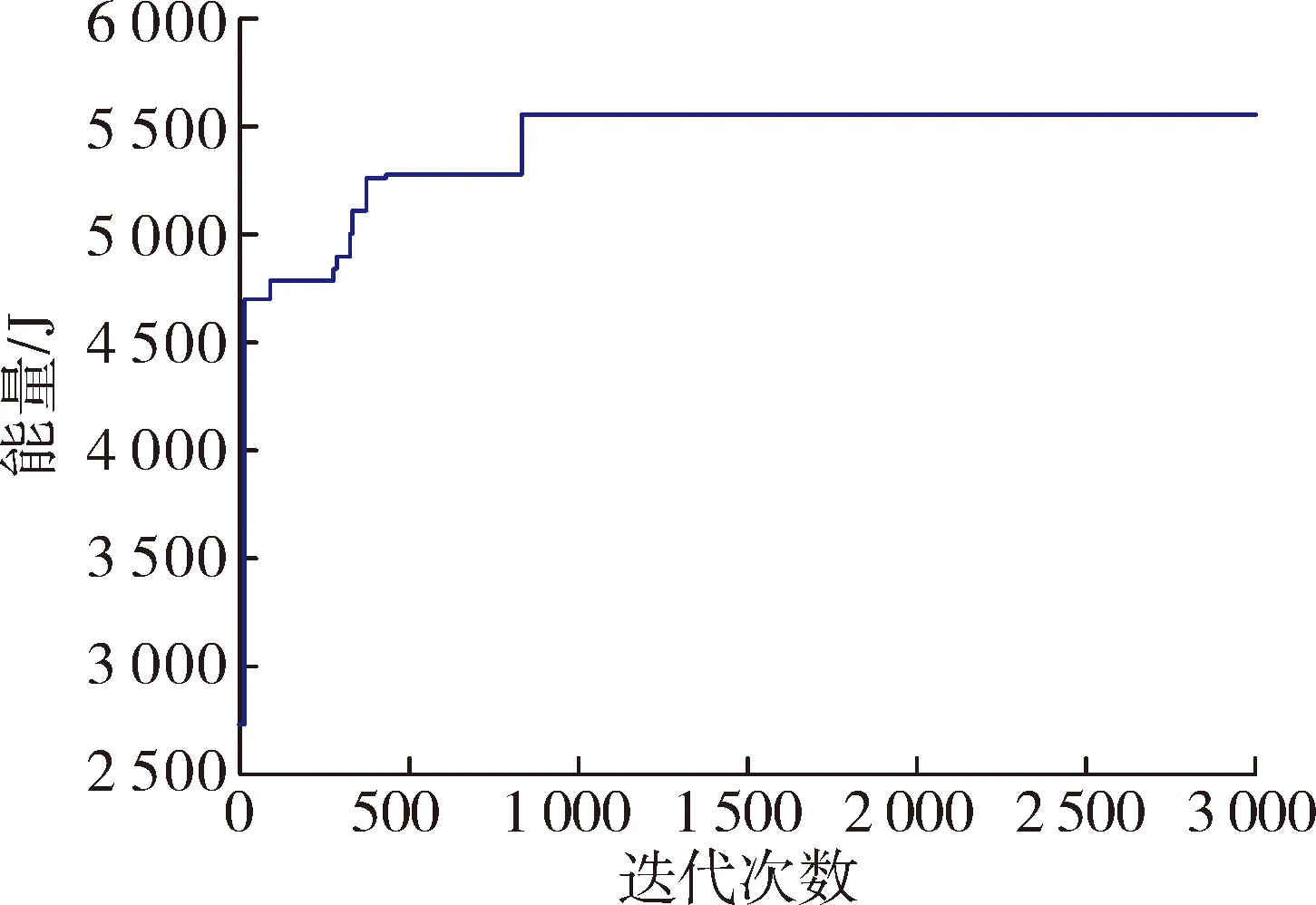
图4 破片能量消耗随迭代次数的变化

由图4可知，随着破片的各参数变化，破片撞击目标靶板消耗的能量增加，迭代到833次后趋于稳定，并稳定在全局最优处。基于战斗部破片各参数设计要求，选取3组有代表性数据如表1所示。

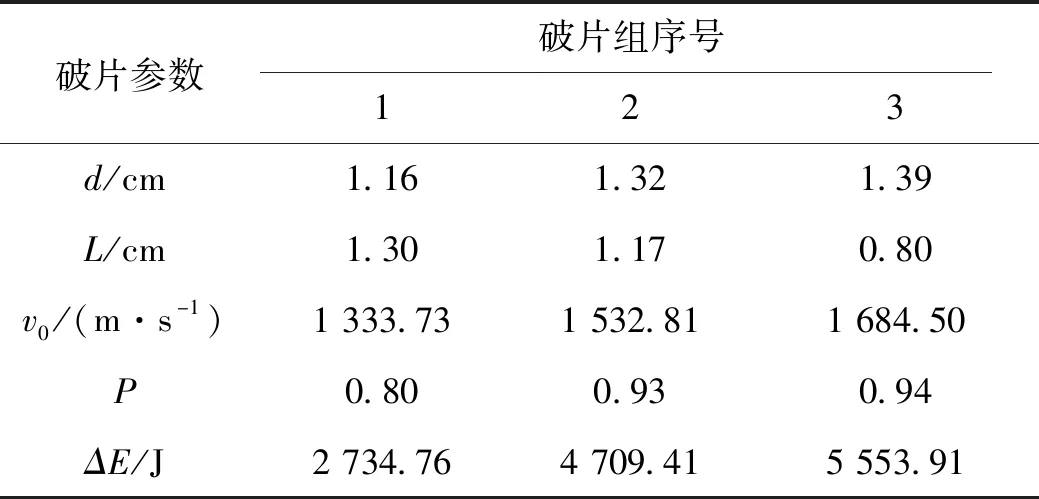
表1 破片参数

通过对表1战斗部破片的参数分析可知，当破片的直径为1.39 cm，长度为0.8 cm，战斗部爆炸后的初速度为1 684.5 m/s时，破片对目标的毁伤概率最大，为94%，破片撞击目标靶板消耗的能量最多，为5 553.91 J。

5 结论

1)对破片飞散特性以及破片与薄靶板的撞击与侵彻行为进行了分析，基于破片能量消耗和比动能双重毁伤准则，建立了破片参数优化分析的双目标规划模型；

2)运用遗传智能算法对本模型进行求解，可以有效控制目标函数的变化趋势，使目标函数最终稳定在全局最优处，并得到全局最优解；

3)算例与分析表明，在破片参数最优的情况下，单个破片对目标的毁伤概率为94%，破片撞击目标靶板消耗的能量为5 553.91 J。若继续增加破片的质量和速度，毁伤概率几乎没有增加，即毁伤作用并没有增大。