基于RID算法的机动目标认知成像方法*

田泰方，张 群，龚逸帅，孙玉雪

(1 空军工程大学信息与导航学院，西安 710077；2 95561部队，拉萨 850000；3 94940部队，江西九江 332100)

0 引言

早期的ISAR技术研究中，假设目标做平稳匀速运动，采用的一种基本方法是距离-多普勒(range-Doppler，RD)算法[1]。实际中目标的运动往往非平稳，这使得传统的RD算法失效。针对这一问题，文献[2]提出了一种面向机动目标ISAR成像的距离-瞬时多普勒(range-instantaneous Doppler，RID)算法，采用时频分析的方法代替传统的傅里叶变换，得到慢时间下的瞬时多普勒谱。2006年S.Haykin提出了“认知雷达”的概念[3]，建立了雷达与外界环境的闭环反馈结构，从而提升了雷达的自适应能力。文献[4]提出了一种MIMO雷达认知波形设计方法，利用有限的发射信号带宽完成了目标高分辨成像；文献[5]提出基于认知成像的雷达资源调度算法，提升了雷达工作效率。然而以上方法均假设目标做平稳运动。

文中针对机动目标的成像问题，提出了一种基于RID算法的认知成像方法。通过对目标进行特征认知获得反馈信息，自适应的调整雷达发射带宽，并实现了在RID算法中利用时频分析进行目标像方位向分辨时的优化重构。仿真实验验证了文中方法的有效性。

1 面向机动目标ISAR成像的RID算法

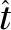
(1)

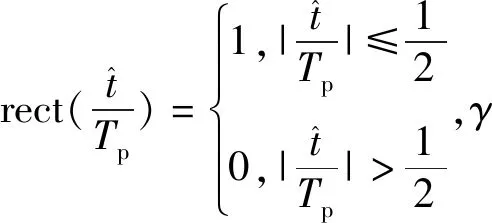
将目标抽象为散射点模型，则在慢时间tm时刻的回波信号为：

(2)

式中:K为散射点数量；σk为第k个散射点的反射系数；Rk(tm)为第k个散射点到雷达的距离；c为光速。

将成像场景中心位置作为参考点，取参考信号为

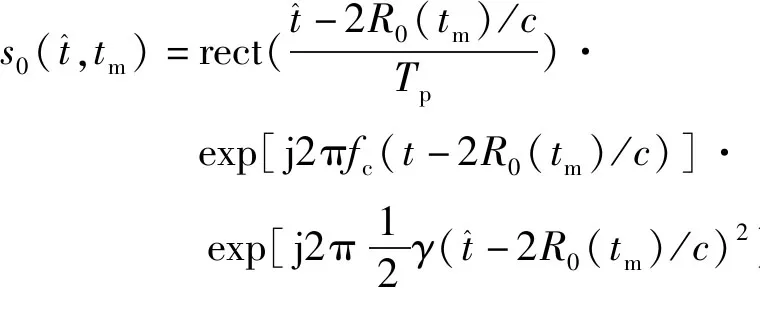
(3)

式中R0(tm)为参考点到雷达的距离。

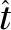
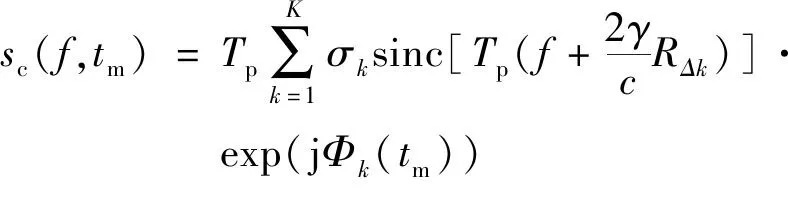
(4)

式中:RΔk=Rk(tm)-R0(tm)，可近似为散射点k相对于参考点的径向距离，相位项Φk(tm)则包含了散射点的方位向信息，需要另外处理。由此可知，对式(4)取模即可得到目标的一维距离像。

根据ISAR成像体制中的转台成像模型[6]，当目标做平稳运动时，各散射点的慢时间多普勒频率与其相对于参考点的横向距离xΔk成正比，有

(5)

因此在传统的距离-多普勒(RD)算法中，仅需对式(4)做关于慢时间tm的傅里叶变换，有

(6)

式(6)即为重构出的目标二维ISAR像。

而对于机动目标，散射点的慢时间多普勒频率是时变的，若直接进行傅里叶变换则会使目标像横向散焦，因此RD算法失效。

时频分析方法可以得到信号频率随时间的变化情况，因此将时频分析引入到RD算法中，替代对慢时间的傅里叶变换，由此得到目标的瞬时多普勒谱，实现机动目标二维成像，这就是距离-瞬时多普勒(RID)算法的原理。

时频分析的方法有很多种，对于LFM信号，具有理想时频集聚性的是Wigner-Ville分布(WVD)，已知信号s(t)，其WVD的定义式为：

(7)

对于载频为fc，调频率为γ的LFM信号，其WVD为：

(8)

然而WVD属于双线性时频分布，对于ISAR回波这种具有多个分量的信号，进行WVD后不仅含有各个分量的WVD，还有分量间的交叉项，影响成像质量。设一含有两个分量的信号是s(t)=x(t)+y(t)，其WVD为：

Ws(t，f)=Wx(t，f)+Wy(t，f)+Wxy(t，f)+Wyx(t，f)

(9)

等式右边的前两项为信号分量x(t)、y(t)的自身项，后两项即为二者的交叉项。

为了保证成像质量，需要对时频分析中的交叉项进行抑制，采用重排平滑伪Wigner-Ville分布(RSPWVD)来替代WVD，其基本思想为加入低通滤波器作为核函数来抑制交叉项，并且把时频分布平面的任一点能量值重排到各能量中心，以此减小加入核函数后给频率分辨率带来的影响[7]。

2 机动目标认知成像方法

在ISAR成像的转台模型体制下，目标的距离像分辨率依赖于发射信号的带宽

(10)

其中带宽B的值在LFM信号中为:

B=γTp

(11)

考虑到雷达的带宽资源是宝贵的，因此将认知成像中的闭环反馈思想引入到机动目标成像方法中，在对目标进行特征认知后，自适应的调整雷达发射信号参数，从而在保证成像质量的前提下提高雷达工作效率。

2.1 基于特征认知的带宽自适应调整

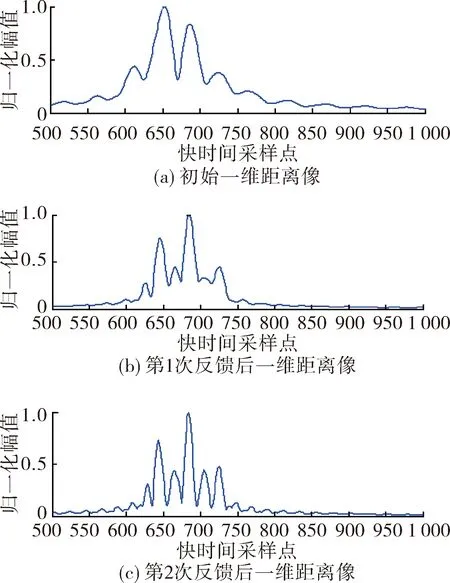
首先设定发射信号的带宽B为一较小的初始值，通过目标反射的少量回波，经过信号处理后得到目标的粗分辨一维距离像sp(f)，对其作归一化处理：

(12)

(13)

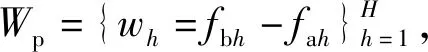
(14)

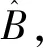
(15)

重复以上的带宽调整过程，直到各散射点在一维距离像上均得到分辨，或带宽达到硬件性能最大值时停止。

2.2 方位向认知多普勒谱估计方法

因此当回波信号的快时间采样点数为N时，为了得到完整的方位向瞬时多普勒谱，就需要进行N次时频分析，这样庞大的计算量难以满足雷达成像实时性的要求。为了缓解这一问题，在此提出一种瞬时多普勒谱认知估计方法。

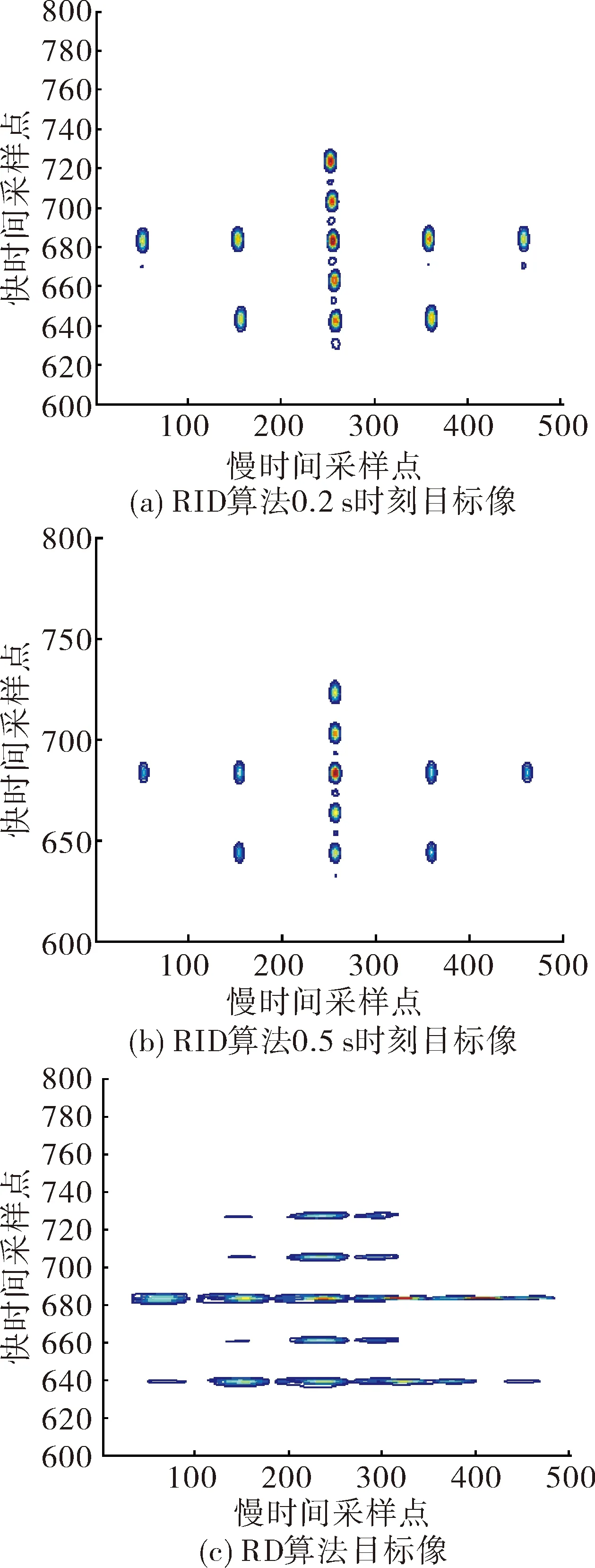
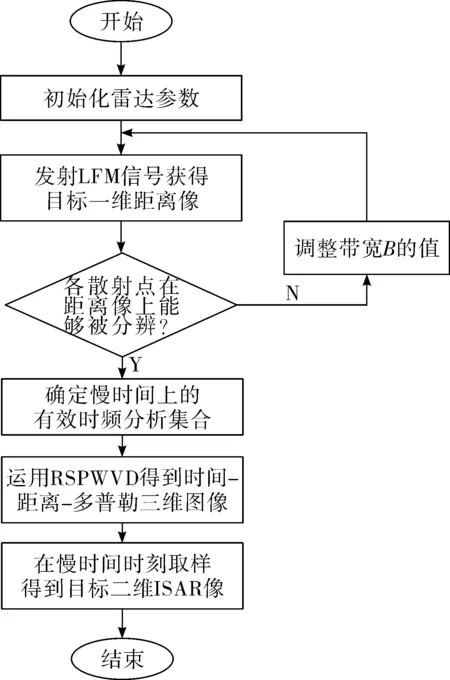
Fe={f|s′p(f)>Ts3，0

(16)

其中N为快时间采样点数，将集合Fe称为有效时频分析集合。

图1 RID算法成像流程图

记集合Fe中的元素个数为NF，接下来对式(4)中的二维函数sc(f，tm)，只需对在自变量f∈Fe范围内，做NF次关于自变量tm的RSPWVD，而在f∉Fe范围内，认为其RSPWVD的值是常数0。由此得到了目标的三维时间-距离-多普勒图像，它包含了在所有慢时间tm=1，2，...，M时刻目标的二维ISAR像，M为慢时间的最大值。例如取tm=m1(1≤m1≤M)，得到该时刻下的ISAR像为：

scm1(f，fd)=WRSP(m1，f，fd)

(17)

3 算法流程

文中提出的基于RID算法的机动目标认知成像方法，流程图如图2所示。

图2 基于RID算法的机动目标认知成像方法流程图

4 仿真分析

设成像雷达发射LFM信号，信号的载频fc=10 GHz，脉冲宽度Tp=10-6s，初始带宽B=10 MHz，脉冲重复频率PRF=500，接收信号信噪比SNR=10 dB。

假设在与雷达斜距R0=2×104m处存在机动飞行目标，沿切向初始速度v=500 m/s，加速度a=5 m/s2，该目标散射点模型如图3所示。

图3 目标散射点模型图

在确定能够提供足够距离像分辨率的带宽后，运用2.2节提出的方位向认知多普勒谱估计方法，得到了有效时频分析集合Fe=[626，743]，其长度Lfe=104。因此接下来只需进行104次时频分析，相对于传统RID算法，减少了计算量(1-Lfe/Nt)×100%=94.8%，这体现了方位向多普勒谱的认知方法，能够有效减少方位向多普勒谱重构的计算量，进而提高机动目标成像实时性。

在有效时频分析集合内，对已经过第3章中步骤2中所述处理后的信号，运用时频分布RSPWVD得到方位向瞬时多普勒谱，取慢时间时刻tm=0.2 s、tm=0.5 s，如图5所示，获得了在这2个时刻目标的ISAR像(见图5(a)、图5(b))，并与RD算法中直接进行方位向FFT获得的目标像(见图5(c))进行对比。

图4 目标一维距离像图

由图5可以看出，相比于直接进行方位向FFT的传统RD算法，采用方位向时频分析的RID算法对机动目标的成像质量明显更好，各个散射点在方位向上均能够被分辨。

定义图像熵H作为算法的成像质量指标，其表达式为：

(18)

式中：|scm(n，m)|为图像中像素点的幅度。图像熵H的值一般小于0，越大代表该图像质量越好，各散射点越能清晰分辨。由此计算得到图5中3幅图像的图像熵计算结果如表1所示。表1中的结果定量证明，采用RID算法的成像质量明显要好于RD算法。

表1 图像熵计算结果

5 结论

针对非平稳运动的机动目标，提出了一种基于RID算法的认知成像方法。依据认知成像中的闭环反馈思想，在目标距离像分辨上提出了特征认知后信号带宽的自适应调整方法；在目标方位向分辨上提出了方位向多普勒谱的认知估计方法。仿真结果表明：文中方法能够节省信号带宽资源、减少成像重构计算量，根据设定的成像质量性能指标与传统方法进行对比，证明了文中方法实现机动目标成像的有效性。

图5 目标二维像对比图