旋转多臂变速运动规律建模及其对开口机构传动影响

袁汝旺， 祝雷雷， 吕雪奎， 杨佳敏

(1. 天津工业大学 机械工程学院， 天津 300387； 2. 天津工业大学 天津市现代机电装备技术重点实验室， 天津 300387； 3. 江苏金龙科技股份有限公司， 江苏 苏州 215500)

开口机构是织机中的一个重要组成部分，常用开口机构包括凸轮开口、多臂开口与提花开口3种形式[1-3]。旋转式多臂机主要由选综机构、提综机构和信息转换机构等部分组成[4]，利用旋转变速机构将织机主轴匀速转动变换为间歇变速回转运动，运行速度已达到1 000 r/min，适用于喷气织机、喷水织机与剑杆织机[5]。

国内外学者对旋转式多臂机研究主要集中在旋转变速机构构型[6]、运动特性与变速运动规律分析等方面。如Stäubli公司提出基于固定凸轮-齿轮、固定凸轮-连杆与固定凸轮-滑块旋转变速机构[7-8]；部分学者研究连杆变速机构[9]、齿轮连杆变速机构[10-11]及其他新型多臂机构[3,12]。在运动特性方面，研究固定凸轮从动件机构分析方法[13]、开口工艺与机构参数关系[14]、多臂开口机构动力学建模方法[15]与仿真[16]等问题；在变速运动规律方面，探讨简谐[2]、摆线[5]、多项式[15]及其组合运动规律模型、参数优化方法及其对综框运动特性的影响[14]。国内外学者对多臂机的研究已取得一定进展，但尚未提出不同旋转变速机构演化与设计方法，需优化旋转变速运动规律以满足不同开口工艺与产品系列化设计。

本文从电子多臂机旋转变速机构构型入手，研究固定凸轮-滑块变速机构运动特性，提出基于绕平行轴转动运动合成的旋转变速机构运动学分析与设计方法，建立适于产品系列化设计的旋转变速运动规律模型与相对运动传动模型，分析参数变化对机构性能与开口工艺的影响，为电子多臂机系列化设计提供理论基础与技术参考。

1 旋转变速机构工作原理

为满足织机开口过程中综框具有一定停顿时间的变速运动的工艺要求，电子多臂开口装置利用旋转变速机构将连续匀速转动转换为具有一定停顿时间的变速回转运动，并经连杆机构驱动综框按照一定规律往复运动。通常织机主轴转速是旋转变速机构转速的2倍，旋转多臂开口为复动式，即旋转变速机构回转1圈，织机完成2次开口过程。图1示出旋转变速机构工作原理。共轭凸轮固定于O点，转盘1绕O点以恒定角速度ω转动，共轭凸轮转子臂2铰接于转盘A点，转子与共轭凸轮保持接触，并驱动转子臂绕A点往复摆动，然后转子臂经滑块驱动偏心连杆构件4-4′做变速回转运动，并通过盘形连杆5最终驱动提综臂6做往复摆动运动。为保证机构运动平稳，旋转变速机构对称安装一对共轭凸轮转子臂。

1—转盘；2—共轭凸轮转子臂；3—滑块；4-4′—偏心连杆；5—盘形连杆；6—提综臂；7—共轭凸轮；8—转子。图1 旋转变速机构工作原理Fig.1 Working principle of rotary shifting mechanism

2 旋转变速机构运动学模型

2.1 旋转变速机构运动特性分析

(1)

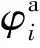
图2 旋转变速机构运动模型Fig.2 Rotary shifting mechanism motion model

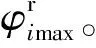
图3 绕平行轴转动的角位移关系Fig.3 Angular displacement relationship around parallel axis.(a) Traction angle displacement; (b) Relative angular displacement; (c) Absolute angular displacement

2.2 旋转变速机构相对运动规律模型

由图3(b)可知，转子臂与偏心连杆绕平行轴转动的相对角位移近似正弦函数，即

(2)

若相对角位移为标准正弦函数的负值，其绝对角位移为摆线运动规律，相对角位移极值出现在φ1=φ0/4与φ1=3φ0/4位置。

为满足不同织造条件下棕框运动特性的差异，对标准正弦函数进行疏密化偏移，调整相对角位移极值的出现位置，获取不同运动特性参数，其疏密化正弦模型为

(3)

式中：a为相对运动幅值调节系数；b为横坐标疏密化调节系数；z=φ1/φ0，z∈[0,1]。

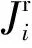
(4)

(5)

(6)

(7)

2.3 相对运动传动模型

由图2可知，共轭凸轮转子臂运动时，通过与其固结的可变连杆AC驱动偏心连杆运动，在△AOC中，根据余弦定理可得：

(8)

(9)

(10)

2.4 共轭凸轮理论廓线模型

由图2可知，B和D的轨迹为控制转子臂相对转动的共轭凸轮的理论廓线，故B与D轨迹坐标为：

(11)

(12)

3 结果与讨论

3.1 旋转变速机构尺寸参数

为分析旋转变速机构运动特性与优化机构尺寸参数，表1示出旋转变速机构的尺寸参数。表中X和Y分别为O与O6在水平和垂直方向的距离。

3.2 偏心连杆运动特性分析

3.2.1 偏心连杆相对运动特性

表1 旋转变速机构尺寸参数Tab.1 Parameters of rotary dobby mechanism

图4 偏心连杆在不同旋转角度和不同b值下的相对运动特性Fig.4 Eccentric link relative movement characteristics with different rotation angle and different b values. (a)Relative angular displacement; (b) Relative analogous angular velocity; (c) Relative analogous angular acceleration; (d) Relative analogous angular jerk

3.2.2 偏心连杆绝对运动特性

当转子臂与偏心连杆相对运动规律已知，由式(1)可确定其绝对运动规律。旋转变速机构回转 1圈，转子臂与偏心连杆绝对角位移为：

(13)

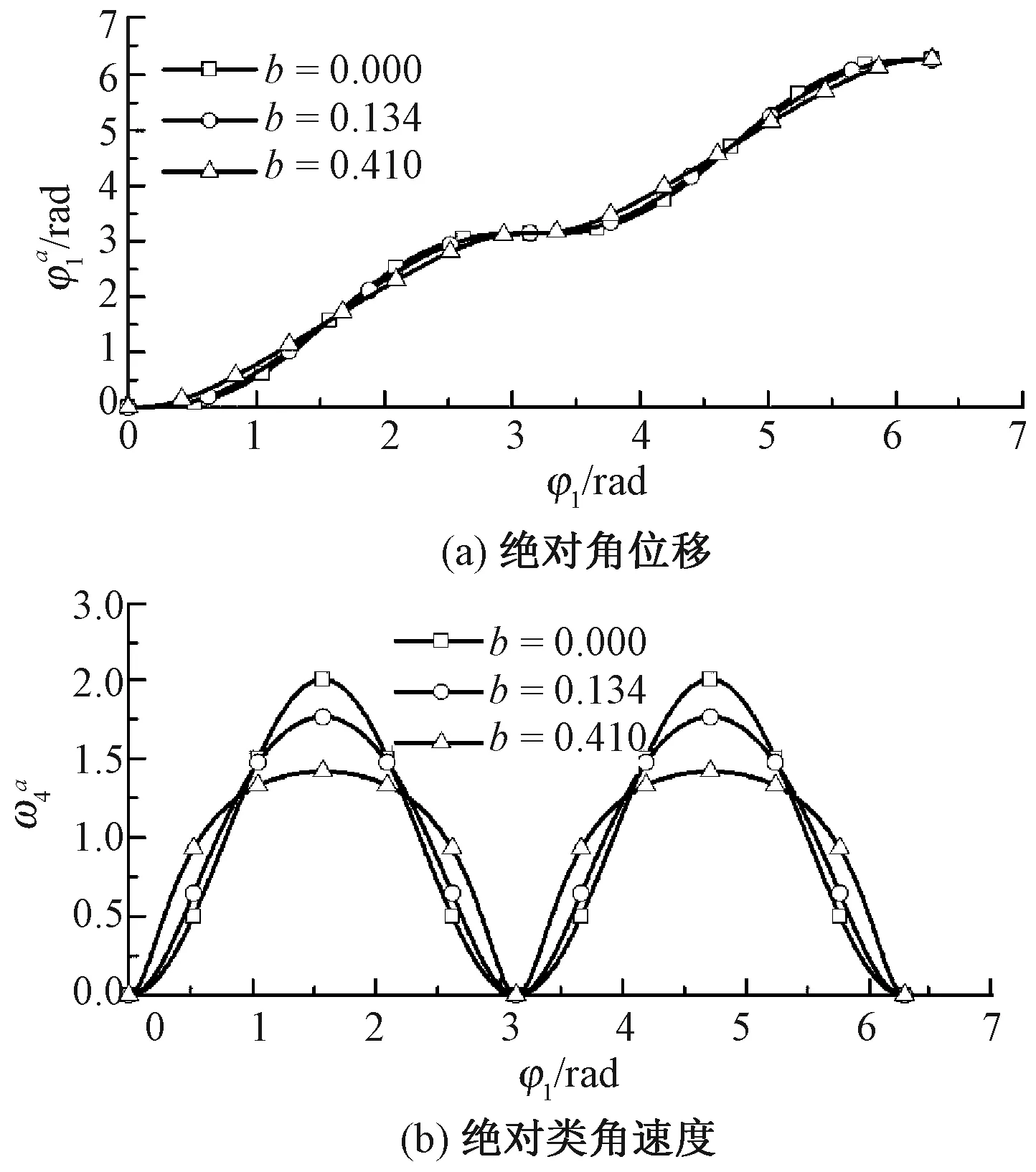
图5 偏心连杆在不同旋转角度和不同b值下的绝对运动特性Fig.5 Eccentric link absolute motion characteristics with different rotation angle and different b values. (a) Absolute angular displacement; (b) Absolute analogous angular velocity

为验证运动规律准确性，利用旋转编码器获取多臂机偏心连杆4的角位移， 并通过数值处理计算偏心连杆4的角速度与角加速度。对数据以转盘转角为参考进行归一化处理，获得偏心连杆4的角位移、类角速度与类角加速度，图6示出实验与拟合数据的对比结果。可知，疏密化正弦运动规律与实验数据具有相似的运动学特性，且当疏密化系数b=0.462时运动特性一致性较好，其中角位移最大误差仅为0.013 4 rad，结果表明了疏密化正弦运动规律的准确性与设计方法的可行性。

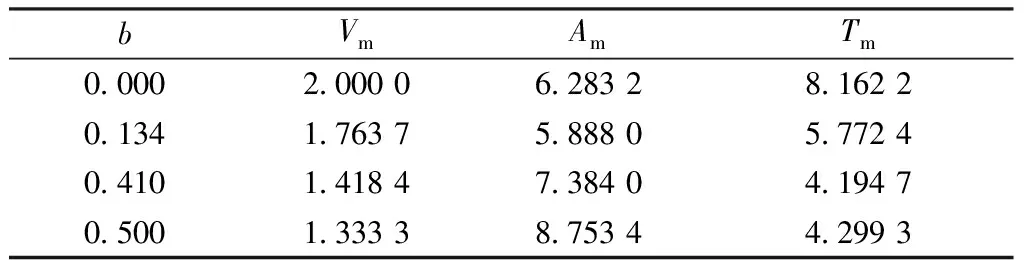
表2 不同b值时偏心连杆的特征值Tab.2 Eigenvalues of eccentric link with different b values

图6 偏心连杆实验与拟合数据对比Fig.6 Comparison of experimental and fitting data of eccentric link.(a) Angular displacement; (b) Analogous angular velocity; (c) Analogous angular acceleration

3.3 偏心连杆长度参数优化

图7 不同l4值时偏心连杆的传动分析Fig.7 Transmission analysis of eccentric link with different l4 values

表3 不同l4值时传动比分析Tab.3 Transmission ratio analysis with different l4 values

3.4 共轭凸轮廓线设计与分析

取l4=60 mm，滚子半径r=31 mm设计共轭凸轮，由式(11)、(12)可得共轭凸轮廓线。图8示出b取值不同时凸轮实际廓线。可知，当b增大，共轭凸轮实际廓线最大极径减小。表4示出b取值不同时凸轮机构参数。可知：压力角与曲率半径均随b增加而减小，当b>0.632 4 时，凸轮廓线出现尖点；当b=0.410 时，凸轮压力角约30°，力传递性能好，适于厚重织物织造。

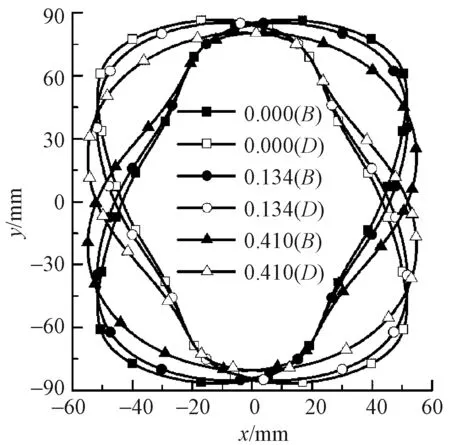
图8 不同b值时凸轮实际廓线Fig.8 Cam actual profile with different b values

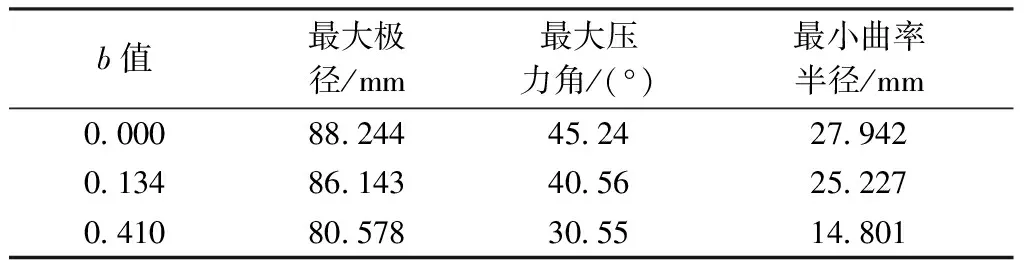
表4 不同b值时凸轮参数Tab.4 Cam parameters with different b values

3.5 提综臂运动特性分析

偏心连杆4与铰接四杆机构的输入构件4′固结，其运动规律相同。图9示出提综臂运动特性。可知：经无急回特性曲柄摇杆机构[17]将旋转变速输出运动转换为具有一定停顿时间的提综臂往复摆动；提综臂的角位移φ6、类角速度ω6、类角加速度α6与类角跃度J6均从0开始，连续变化无突变，利于综框高速运动，避免震荡；随b增大，提综臂最大角位移保持不变，但在最大位移处停顿时间减少；类角速度、类角加速度与类角跃度随b增加而减小，利于减小凸轮外形尺寸，提高织造速度，降低综框运动冲击与适应复杂负载，实现减震降噪；根据织物特性、速度与引纬时间等工艺要求合理选择b，即可获得满足不同织造工艺的共轭凸轮。

图9 不同旋转角度时提综臂运动特性Fig.9 Jacklever motion characteristics with different rotation angle. (a) Angular displacement; (b) Analogous angular velocity; (c) Analogous angular acceleration; (d) Analogous angular jerk

引纬时间是织造的重要参数，获取更长的引纬时间利于阔幅织物织造并提高生产效率。表5示出不同b时提综臂停顿时间。设定阈值m，提综臂阈值角位移φ61=mφ6max，阈值角位移与提综臂角位移曲线相交于M、N这2点，其所对应的织机主轴转角差即为提综臂近似停顿时间；阈值相同时，随b增大，提综臂停顿时间减小；b相同时，随阈值m减小，提综臂停顿时间增大；以b=0.410为例，m取值为1.000、0.990、0.975和0.950时，综框停顿时间分别占运动周期的15.56%、18.33%、20.56%和22.50%。

表5 不同b值时提综臂停顿时间Tab.5 Jacklever suspension period with different b values

合理选择运动规律的疏密化调节系数，可满足不同织物负载、速度和幅宽等工艺参数要求的差异。在实际生产中仅通过更换凸轮就可满足不同的工艺要求，实现电子多臂机的系列化设计。

4 结 论

1)从旋转变速机构构型入手，分析固定凸轮-滑块变速机构运动特性，提出基于绕平行轴转动运动合成的旋转变速机构运动分析与设计方法，建立适于产品系列化设计的旋转变速疏密化正弦运动规律模型，为旋转式多臂机系列化设计提供理论基础。

2)从旋转变速输出规律出发，建立转子臂与偏心连杆的相对运动传动模型，提出凸轮廓线设计方法及其机构评价指标。结果表明：转子臂与偏心连杆相对运动传动近似等角速比，随疏密化调节系数增加，凸轮最大极径、压力角和曲率半径均减小。当疏密化调节系数取0.410时，偏心曲柄获得扭矩最优的运动特性，可用于复杂负载时的纺织。

3)旋转变速输出规律经连杆机构转化为提综臂具有一定停顿时间的往复摆动；提综臂运动特征值从0.000开始，连续变化无突变，利于综框高速平稳运动；随疏密化调节系数增加提综类速度、类加速度与类跃度及其相对主轴静止时间减小；随阈值减小，提综臂相对主轴静止时间增加，但静止时间变化率较小，合理选疏密化调节系数适应不同织物负载、速度和幅宽等工艺参数差异。