基于改进的加权中值滤波与K-means聚类的织物缺陷检测
2019-05-27张缓缓马金秀景军锋李鹏飞
张缓缓, 马金秀, 景军锋, 李鹏飞
(西安工程大学 电子信息学院, 陕西 西安 710048)
作为衣着、装饰、医用、产业用、航天军工用品的原料,织物是生活与工业生产中不可或缺的材料,在织物生产中,由于纱线瑕疵、机械故障、人工操作失误以及生产环境干扰等因素,不可避免地会产生织物缺陷。缺陷的存在对纺织终端产品的质量及价格有着决定性影响,如果缺陷产品应用于航空、军工及医用中,将造成不可估量和无法挽回的损失,因此,织物缺陷检测尤为重要。然而由于各类织物纹理结构复杂,噪声和细微缺陷之间相似性高,极大增加了缺陷检测的难度。目前绝大部分的纺织企业依赖人工视觉检测织物缺陷,传统的人工检测易受个人视力、疲劳状况、情绪、光照等主客观因素的影响,往往无法确保检测的精度及准确率,尤其对于纹理复杂、图案花型多变、颜色差异较小的缺陷,人眼几乎不能识别,远远不能满足工业生产应用的需求。探索一种有效、具有普适性的织物疵点检测方法,使其能够快速且准确地识别各种印花织物的疵点,具有重要的学术价值和应用价值。
近年来,针对织物疵点的检测算法主要包含 4种方法。基于统计的方法主要包括分形维数、互相关、共生矩阵、局部二进制模式:Conci等[1]运用分形维数理论检测织物瑕疵;朱丹丹等[2]采用自相关算法计算各个纹理基元和标准模板的相似度,评估格子织物图像中有无瑕疵纹理基元;然而该类方法对纹理周期性不强的织物检测效果差。基于频谱的方法近年来被广泛应用于瑕疵检测,主要包括Gabor滤波器[3-4]、小波变换[5]和傅里叶变换[6]:Kumar等[7]研究了几种不同的利用Gabor小波特征进行纹理材料表面检测的方法;Tsai等[8]利用傅里叶模型提取织物瑕疵的傅里叶特征,进而实现疵点分割;该类方法可有效提取瑕疵的特征,但对于方格条纹织物检测效果不佳,自适应性不强。基于模型的方法有自回归模型、马尔科夫随机场模型等:Hajimowlana等[9]使用一维自回归模型提取误差区域生成疵点形状;李敏等[10]应用改进的高斯混合模型,通过分块建模思想有效识别出彩色纹理织物表面疵点;可以看出,基于模型的方法适合织物纹理之间的分类,虽然可识别纹理结构相对简单、颜色单一的织物瑕疵,但在瑕疵识别研究中相对于统计法和频谱法应用较少,另外该类方法的算法复杂度高,检测时间较长。基于学习的方法常见的有应用卷积神经网络、自编码网络[11]:Yapi等[12]提出了一种新颖的基于监督学习的方法;Tsang等[13]提出的Elo评级方法,在点形和星形图案的织物图像中被证明有很好的效果;Li等[14]基于Fisher准则将含有疵点和不含疵点的织物图像进行分类,表明该方法在复杂的提花经编织物上有更好的结果;基于学习的方法需要观测者对大量图像进行标记质量分数来训练模型参数,而主观标记质量分数存在不精确、费时耗力等缺陷。
综合以上分析可知,现有检测方法很难有效描述复杂多样的织物纹理,且具有很高的运算复杂度,自适应性不强,致使检测效果不明显。针对织物组织纹理结构复杂、花型繁多、材质多样的特点,如何有效检测出疵点仍然是研究的热点。本文提出改进的加权中值滤波与K-means聚类相结合的方法,以提高算法对不同织物纹理的适应性,在抑制背景纹理的同时通过联合直方图以及中位跟踪平衡算法显著提高滤波速度;利用K-means聚类标记出疵点与非疵点区域,以检测方格、点形、星形、平纹、斜纹等各种纹理织物的疵点。
1 织物疵点检测方法
本文织物疵点检测流程图如图1所示。首先采用快速加权中值滤波对图像进行平滑处理,改善织物纹理和噪声对疵点检测的影响,并提高图像预处理速度;其次,利用K-means均值聚类算法对平滑之后的图像进行聚类,将图像标记为疵点区域和非疵点区域,进而实现瑕疵的检测。
1.1 加权中值滤波
织物纹理是织造过程中纬线与经线有规律的交织形成的周期结构,具有随意多样的特点,这给织物疵点的检测带来很大的困难。加权中值滤波处理织物疵点图像可更好地保留疵点特征信息。
加权中值滤波器可看作是一个运算符,是用本地窗口中相邻像素的加权中值替换当前像素。形式上,在处理图像I中的像素p时,仅考虑以p为中心,半径为r的局部窗口R(p)内的像素,与传统未加权中值滤波器不同,对于每个像素q∈R(p),加权中值滤波基于对应特征图f中像素p和q的亲和度将其与权重Wpq相关联,如式(1)所示。
Wpq=g(f(p),f(q))
(1)
式中:f(p)和f(q)为f中像素p和q处的特征;g为相邻像素之间的典型影响函数,可以是高斯 exp{-‖f(p)-f(q)‖} 或其他形式。
将I(q)表示为图像I中的像素q和n=(2r+1)2处的值作为R(p)中的像素数,将R(p)中的所有像素的值和权重表示为(I(q),Wpq)。按升序的规则对值进行排序,像素p的加权中值运算符返回一个新的像素p*,I(p)由I(p*)代替。这个过程得到的p*如式(2)所示。
(2)
式中,k为像素数。该定义对于p*之前的所有像素,意味着相应权重的总和应该是所有权重相加的一半,f映射通过式(2)确定权重。
1.2 改进的加权中值滤波
加权中值滤波处理纹理织物疵点图像时不能解决重复进行访问排序的问题,比较耗时,在疵点检测实时性要求较高的情况下难以应用,因此,采用以下方法改进加权中值滤波[15],减少背景纹理信息对检测的影响,同时提高检测速度以满足工业生产的需求。
1.2.1 联合直方图
将联合直方图与滑动窗口策略相结合,以实现预处理速度的提升。联合直方图是一种常规但非常有效的二维直方图结构,用于存储像素数,如图2所示。在2-D联合直方图H中,将像素q放入第f行和第i列的直方图中,整个联合直方图构造如式(3)所示。
我父亲1918年初生人,属马。要是活着今年整一百岁了。我奶奶家当年是做生意的,经济上挺富裕。1916年她16岁那年,在读私塾的时候认识了我爷爷。当时我爷爷家境并不好,只因为他叔叔是教书先生,他才能跟着读私塾。那个年代婚姻都是家长做主,可我奶奶有大小姐脾气,再加上民国了读书了,思想相对开放了,非要嫁我爷爷不可。一来二去,家里看实在拦不住了,只能勉强同意。转年,我爷爷家下了聘礼,我奶奶下嫁了我爷爷。
H(i,f)=#{q∈R(p)I(q)=Ii,f(q)=ff}
(3)
式中:运算符#为计算元素的数量,该计数方案即使在窗口移动时也能实现权重的快速计算。对于属于窗口中(i,f)的任何像素,考虑滤波器中心p,其权重可立即计算为g(ff,f(p)),通过遍历联合直方图,可获得像素权重值为i的所有像素的总权重,如式(4)所示。
(4)
式中,Nf为不同特征的总数。
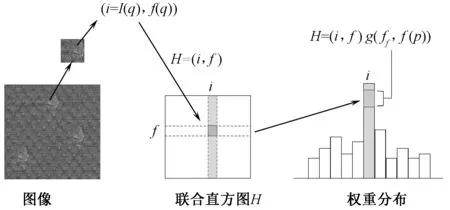
图2 联合直方图图解Fig.2 Joint-histogram illustration
算法以扫描线顺序处理输入图像,每个位置执行2个步骤。步骤1为中值查找:首先遍历联合直方图,根据式(2)计算权重,将他们相加得到第1遍的总权重wt;然后进行第2遍遍历,计算总权重wt的一半的加权值,并输出相应的像素值。步骤2为移位和更新:如果不是此图像的结尾,将滤波窗口移动到下一个位置。计数离开窗口的每个像素相应减少的单元格,每移出1个像素就增加1个来更新联合直方图。
算法加快了中值滤波效率,但由于步骤1需要遍历直方图,占用更多的时间。为进一步改善,采用中位跟踪平衡算法,使步骤1能够加速到300~2 000 倍。
1.2.2 中位跟踪平衡算法
根据定义,在累积权重达到总权重一半的位置处得到加权中位数,在当前滤波器中认为在该位置找到加权中值并作为切点c,如图3所示。其中左边的权重总和等于右边权重的总和,wl和wr之间的差异接近于零,有助于通过求解找到加权中位数。
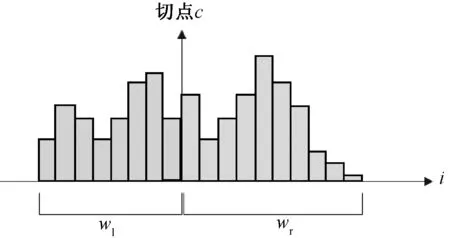
图3 切点与平衡点的分布Fig.3 Illustration of balance and cut point
使用平衡算法,可直接获得窗口的平衡点b,如式(5)所示。
(5)
式中,B(f)测量c两侧特征ff的像素数是否平衡。通过计算像素数差异的轻量级平衡度量,可判断是否找到加权中位数,以此代替累积权重算法。
1.3 K-means聚类
预处理削弱了织物纹理背景的影响,疵点得以突显,同时分析织物本身的特性可知,织物疵点图像可看作是疵点和织物纹理二类簇的叠加。根据该特点,采用K-means算法对预处理后的图像实现织物疵点的分割,如图4所示。

图4 K-means算法对织物疵点进行分割Fig.4 Segment of fabric defect by K-means. (a)Texture part; (b)Defect part; (c)Fabric defect image
设xi为簇Ci中的数据对象,ci为簇Ci的中心点(均值),通常所用的目标函数如式(6)所示。
(6)
式中,Je为输入数据对象与其所在簇的中心点的平方误差总和。
K-means算法过程如下:1) 随机选择k个对象作为初始聚类中心;2) 计算每个样本点到各个聚类中心的欧式距离,以距离为依据将各个样本点分配到与其最近的类中;3) 重新计算每个类别所有样本点的均值,更新聚类中心;4) 重复过程(2)、(3),直到目标函数收敛为止。
利用K-means聚类算法的特性,对织物图像的像素灰度值进行聚类计算,判断织物图像的像素值属于疵点类别还是非疵点类别,实现缺陷的分割。
2 结果与讨论
为验证所提出的纹理织物疵点检测算法的可行性,采用香港理工大学自动化实验室[16]的3类图案织物(方格织物、点形织物、星形织物)样本及德国TILDA织物纹理数据库其他类型的织物疵点样本进行测试。
在中值滤波阶段,影响检测结果的2个参数为:改进的快速加权中值滤波的r(窗口半径)和σ(标准偏差的高斯内核值)。以方格织物为例,分析各参数对织物图像检测结果的影响,如图5所示。可知:窗口半径r越小,织物背景纹理对检测结果的干扰较大;而r过大又会造成检测结果失真,故选取r=13.0。图6示出不同σ值对应疵点检测结果。可知:σ越小,背景纹理越不易被抑制,疵点检测越困难;σ越大,检测到的疵点面积有所变化,部分背景被当作疵点区域检测出来,导致疵点区域过于完整与连续,故选取σ=135.0。针对不同纹理类型的织物,其参数选择不同。参数范围如表1所示。

图5 不同窗口半径r对应的检测结果Fig.5 Detection results of different r. (a)Grid beheaded; (b) r=10.0; (c) r=13.0; (d) r=15.0

图6 不同σ值对应的检测结果Fig.6 Detection results of different σ. (a) Box-patterned oil; (b) σ=100.0; (c) σ=135.0; (d) σ=500.0

表1 改进的快速加权中值滤波的参数设置Tab.1 Parameters setting for modified faster weighted median filter

图7 本文方法对部分方格点形及星形织物样本检测结果Fig.7 Some results of square, dot, star fabric defect detection by method of this paper. (a) Fabric original image; (b) Result by using improved weighted median filtering; (c) Detection result
实验过程中选择多种纹理的多种疵点进行检测,其部分检测结果如图7、8所示。同时,将本文方法与文献[3]所述的Gabor滤波法、文献[17]所述的Frangi滤波器和模糊C均值结合的方法进行比较,结果如图9所示。由图9(b)可知,Gabor滤波法不能完全地去除纹理对检测结果的影响,噪声干扰比较大;由图9(c)可以看到,疵点区域膨胀或者部分疵点区域丢失,对疵点的细节信息检测不准确,所以Frangi滤波器和模糊C均值结合的方法不能很好地看到效果。综上,本文提出的改进的快速加权中值滤波不仅可很好避免背景纹理的干扰,突出疵点信息,而且使用 K-means 聚类后能更清晰地突出疵点,可视化较好,准确率高(见图9(d))。
为验证算法的分割精度,利用准确度(ACC)、真阳性率(TPR)、假阳性率(FPR) 3个参数进行量化对比,如式(7)~(9)所示。
(7)
(8)
(9)
式中:TP为真正例;FN为假反例;FP为假正例;TN为真反例。
算法对每种类型纹理织物采取120张图片进行测试,求取检测结果平均值。表2示出不同类型的纹理织物的疵点检测所用的平均时间,检测结果准确率对比如表3所示。
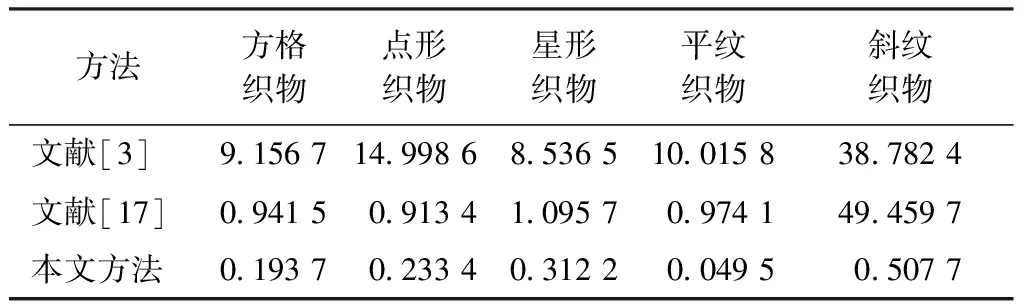
表2 使用不同方法检测所用平均时间Tab.2 Comparison of average time by three different methods s
由表2和表3可以看出,本文提出的方法检测准确度可高达到97%,整体可靠度水平较高。从算法的执行速度来看,本文所提出的方法在检测各类纹理织物时,与文献[3]、[17]方法相比,检测时间明显缩短。
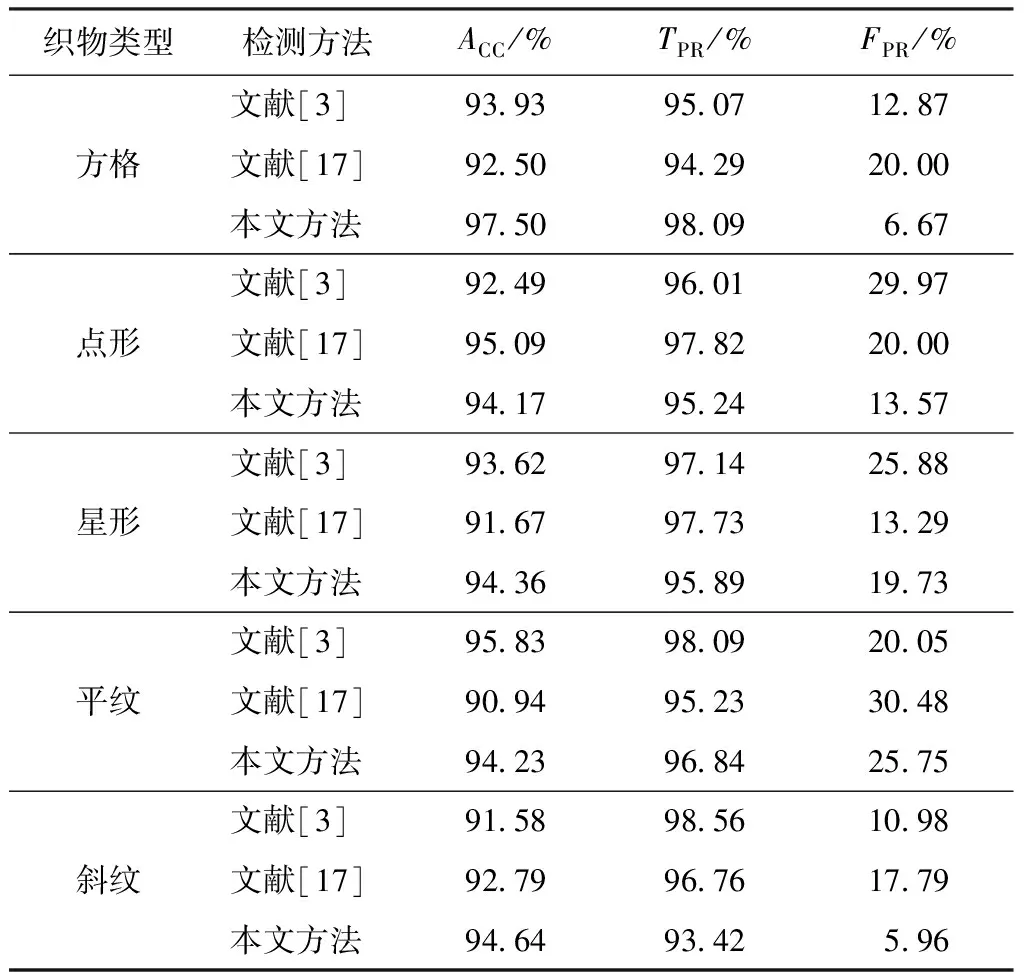
表3 使用不同方法的准确率对比Tab.3 Comparison of accuracy by three different methods
3 结 论
为减少织物纹理信息对疵点检测的影响,对中值滤波进行改进,将联合直方图与滑动窗口策略相结合,实现预处理速度的提升;利用K-means聚类算法将织物的疵点和非疵点进行分类检测,避免复杂的确定分割阈值环节,直接完成疵点检测,进一步提升了检测效率;本文提出的方法可对方格、点形、星形、平纹、斜纹等纹理织物的疵点进行检测。实验结果表明提出的方法效果较好,具有较高的可靠性。
