基于遗传算法的末端配送优化——以M快递点部生鲜配送为例

杨丽英，黄汉强，杨从平

一、引 言

艾瑞咨询发布《2018年中国生鲜电商行业消费洞察报告》一文显示，2017年中国生鲜电商市场交易规模约为1391.3亿元，同比增长59.7%，预计2018年交易规模达到1947.8亿元[1]。与此同时，天猫、京东、苏宁易购等大型网上购物平台全面涉足生鲜市场的同时还致力于布局冷库建设与冷链配送，这些数据均表明人们对生鲜产品的需求量呈现出快速增长的发展趋势，而由此带来的生鲜电商配送问题亦成为企业、学者专家研究和关注的热点问题。

Hsu C等人（2011）对蓄冷箱式多温共配系统与传统多车配送方法进行比较分析，提出适合城市末端配送的蓄冷箱式多温共配系统方案[2]。詹斌等人（2016）借助云计算和大数据等先进的互联网技术对电商物流末端配送进行系统地分析，提出可视化配送服务、合作共用自提柜、无人机送快递等一系列创新思路[3]。申风平等人（2017）则采用熵值法和灰色绝对关联度进行分析，提出管控生鲜配送风险的有效性策略[4]。

在实际生活中，生鲜配送属于末端配送，是二次投递，本文结合生鲜末端配送特点，选取M快递点部其生鲜配送路径问题，构建以配送成本最小的优化模型（最终转化为路径最短的优化模型），利用遗传算法在路径优化的便捷性与有效性对其配送路线进行路径优化，以此来求解出具体的生鲜末端的配送路线。

二、M快递点部生鲜末端配送现状及问题分析

（一）M快递点部生鲜配送现状分析

M快递点部的仓库位于南宁市竹溪大道43号容桂商厦一楼，仓库占地面积250平方米，其配送业务主要集中在各类网购快递包裹和生鲜配送。配送设备主要是13辆三轮车及37辆两轮电动车。其中生鲜配送采用两轮电动车进行配送，承诺在两个小时左右送达给客户。另外设有3个冰柜以满足当客户需要滞留生鲜产品时对生鲜产品进行冷藏，保证其新鲜度，配送的生鲜种类产品如表1。

表1 M快递点部配送的生鲜产品种类

从表1生鲜产品种类来看，水果类具有较明显的季节性，所以M点部的生鲜配送量会在每年的5—7月有明显增加。此外，在整理M点部2015—2017年近三年的生鲜配送量数据中，不难发现人们网购邮寄生鲜产品数量在逐年上升中，具体见图1。

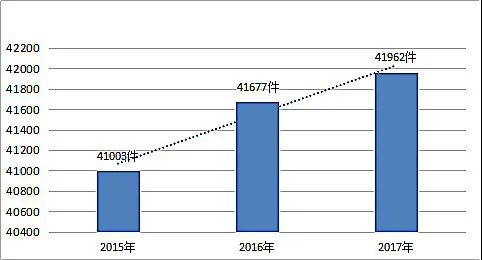
图1 2015—2017年M点部生鲜配送数量变化情况

从图1可以看出M快递点部生鲜配送逐年增长，但增幅较小。其原因主要是位于该点部成熟老城区，周边生活配套完善，各类生鲜产品购买便利，而客户开发容量有限，需要增加新配送模式，提升配送附加值才能吸引有限客户群的购买配送需求，从而使得更多客户愿意网购生鲜产品，进而提高点部的生鲜配送量。

（二）M快递点部生鲜配送的问题分析

在M点部运营中存在许多不可控因素，在降低运营成本过程中可能就会带来不利于生鲜产品配送的问题，如：未满载就发车、缺乏温控设施、存在二次投递质量无法保证、不适混载的配送等，造成资源浪费、产品变质等问题。同时，由于承诺两小时送达服务，现M点部的生鲜配送基本上到件分拣后就开始派送，缺乏合理的配送规划而造成人员浪费，多人送、线路重合，使得配送效率低下。

为了解决这类由于多人送、线路重合的配送效率低下的问题，即以最低配送成本作为最终优化目标，其配送成本包括运输成本、固定成本和货损成本，其中运输成本和货损成本与配送的里程存在正比关系。在结合实际情况忽略一些因素的情况下，可以将配送成本最低转换为以配送路程最小作为最终的优化目标。本文借助MATLAB软件进行遗传算法的路径优化，计算出M点部在采用两条配送线路时，如何更好地完成9个客户点的配送任务。

三、M点部生鲜配送路径优化模型构建假设

（一）模型思路

所谓路径优化目标，就是指在满足一定的约束条件（比如对装载量、配送量、配送时效、收货或发货时间等进行条件的限制）情况下，生鲜产品的配送员按照设定好的路线进行配送服务，最终能够实现既定的目标（比如总里程最短、总费用最低、总配送车辆数量最少、总配送时间最短等）的过程。

由于生鲜的配送需要考虑到时效性问题，因此，对路径的选择上需要采用严格而科学的方法才能更好地进行理论支撑及分析。因此，在构建配送路径优化的模型中，为了使模拟出的计算结果更加符合实际的要求，本文将主要采用遗传算法进行配送路径的优化。

（二）模型的假设和约束条件

1.假设条件

为了便于对路径进行计算研究，将配送员进行生鲜配送过程中的问题能够转化为可以求解的数学模型，使得计算机的模拟结果与实际结果更加接近，此时需要对生鲜配送人员在配送过程中做出假设：

（1）点部能够给各个客户点进行配送；

（2）进行生鲜配送的车辆规格以及行驶速度相同；

（3）配送车辆只从M点部出发，完成配送任务后必须回到点部，最终形成闭合回路；

（4）每个配送员对各个配送客户的配送路线是已经安排好的路线；

（5）当客户不在家或者拒签时，订单会返回点部；

（6）地点简化为一个点，以便得出具体的位置信息。

2.约束条件

模型的构建，需要满足以下约束条件：

（1）每辆配送车的实际载货总量不大于该车的最大载货量；

（2）单个客户仅对应一个配送车辆的服务；

（3）车辆在完成上一个客户点的配送后一定要给下一个客户点配送或者返回到M快递点部。

（三）模型的建立

1.目标函数的构建

在生鲜产品的配送过程中，由于生鲜产品具有非常鲜明的时效性和易腐性，因而在实际的配送过程中必然会存在着生鲜的损耗问题，这样会直接导致配送成本以及配送车辆成本的增加。因此，为能够建立合理有效的目标函数，本文在考虑生鲜产品自身存在的鲜明属性前提下，将配送成本最小化作为最终的优化目标。此时，在对构成配送总成本进行系统地分析：一是在配送过程中，车辆使用成本以及运输成本是必然产生的费用；二是在配送过程中由于生鲜产品具有非常鲜明的时效性和易腐性，会在配送过程中会造成生鲜产品的损失，这称为货损成本。综上所述，本文所构造的模型中总的配送成本主要是由固定成本、运输成本、货损成本组成。

（1）固定成本

配送员在进行配送的过程中使用到的电动车会产生一定的费用，主要是由车辆的保养费、维修费及人工费用等构成。这部分的成本一般是固定的，与行驶的时间和路程无关，用代表固定成本，则有：

式中：C1——完成单次配送任务的电动车所消耗的固定成本；m——配送车辆的数目。

（2）运输成本

配送员在配送过程中使用到的电车会产生一定的成本，这部分费用主要由电车充电所消耗的电费以及进行维修保养费。运输成本费用主要是由行驶的路程决定，在优化该部分的成本时，可以对行驶路程进行考虑。因而，用与运输距离成正比例关系的函数表示运输成本函数，用Ct表示运输成本，则有：

式中，C1——电车每行驶一公里产生的费用；

dij——客户i和客户j之间的实际距离；

Xijk——0-1 变量，若车辆 k 在路段（i，j）上行驶，则Xijk=1，否则Xijk=0。

（3）货损成本

货损成本是指在生鲜产配送过程中，由于时间、温度等一系列不可控因素引起生鲜产品质量的下降，造成生鲜产品损失而需要额外支付的费用。运输过程中温度、时间是造成货损成本的根本原因，但是在顺丰琅西点部配送过程中没有控制温度设备的保障，此时不把温度划入考虑范围，因此在考虑生鲜货损成本时，可以用与运输距离成正比例关系的函数表示货损成本函数。

2.优化模型的构建

根据对上述目标函数的分析，在构建以配送总成本最低为最优目标的情况下，固定成本一般是固定的，与行驶里程和在途时间无关，但是运输成本和货损成本都与配送的距离存在着正相关的关系，因此，模型中的最优目标可以将配送总成本最低转换为配送的总路程最小，于是可以认为在模拟计算中路径最小就是配送成本最低，经过目标函数的转换后不仅能简化计算，还能够保证模型及模拟计算的准确性。

四、基于遗传算法的M快递点部生鲜配送路径优化

（一）基础数据

M点部的生鲜配送主要集中在以下9个客户（A-J）点，文中将选取这9个客户点作为模型中的配送点，在以单一固定的生鲜配送中心形式，主要考虑载重量（该快递点部车辆的最大载重量为500kg）及车辆数的约束下，通过MATLAB模拟出最佳的生鲜配送路径，最终实现科学、合理地将生鲜配送到各个客户手上的目标。配送中心（其标号为“M”）及9个客户的位置坐标数据（经纬度坐标由百度地图查询得到）、客户对生鲜产品的需求量如下表2所示。

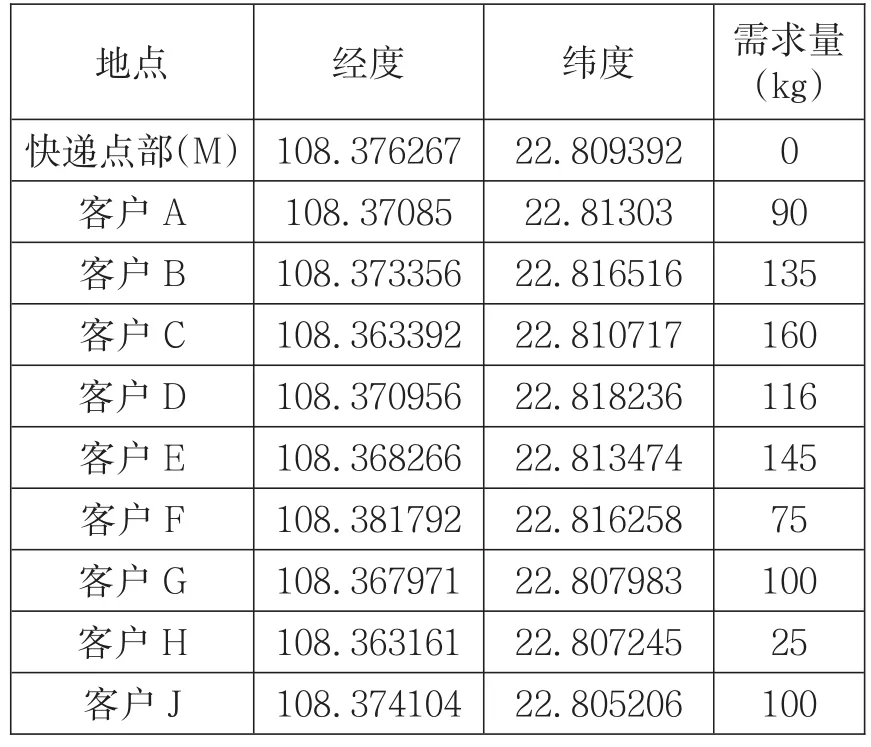
表2 快递点部9个客户（A—J）位置及需求信息表

将其具体的位置信息通过MATLAB表现出来如下图2所示。

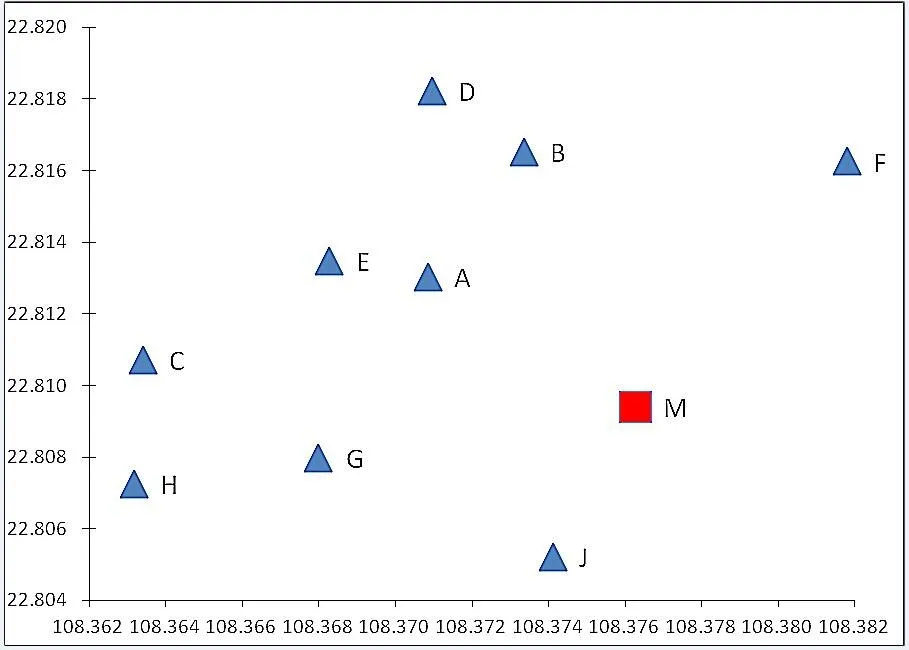
图2 M点部配送中心及9个客户（A—J）位置坐标图

（二）假设及约束条件

为了便于对路径进行计算研究，将配送员进行生鲜配送过程中的问题能够转化为可以求解的数学模型，使得计算机的模拟结果与实际结果更加接近，此时需要对生鲜配送人员在配送过程中做出假设及约束。其中假设：

1.假设条件

（1）点部能够给各个客户点进行配送；

（2）进行生鲜配送的车辆规格以及行驶速度相同；

（3）配送车辆只从顺丰琅西点部出发，完成配送任务后必须回到点部，最终形成闭合回路；

（4）每个配送员对各个配送客户的配送路线是已经安排好的路线；

（5）当客户不在家或者拒签时，订单会返回点部；

（6）地点简化为一个点，以便得出具体的位置信息。

2.约束条件

（1）每辆配送车的实际载货总量不大于该车的最大载货量；（2）单个客户仅对应一个配送车辆的服务；

（3）车辆在完成上一个客户点的配送后一定要给下一个客户点配送或者返回到M点部。

（三）基于MATLAB的计算过程

由于在实际配送中，两客户点间的距离不是单纯两点之间的距离，本文采用百度地图对上述9个客户点进行测量，得出它们之间的距离，具体的距离矩阵（单位：km）如表3所示。

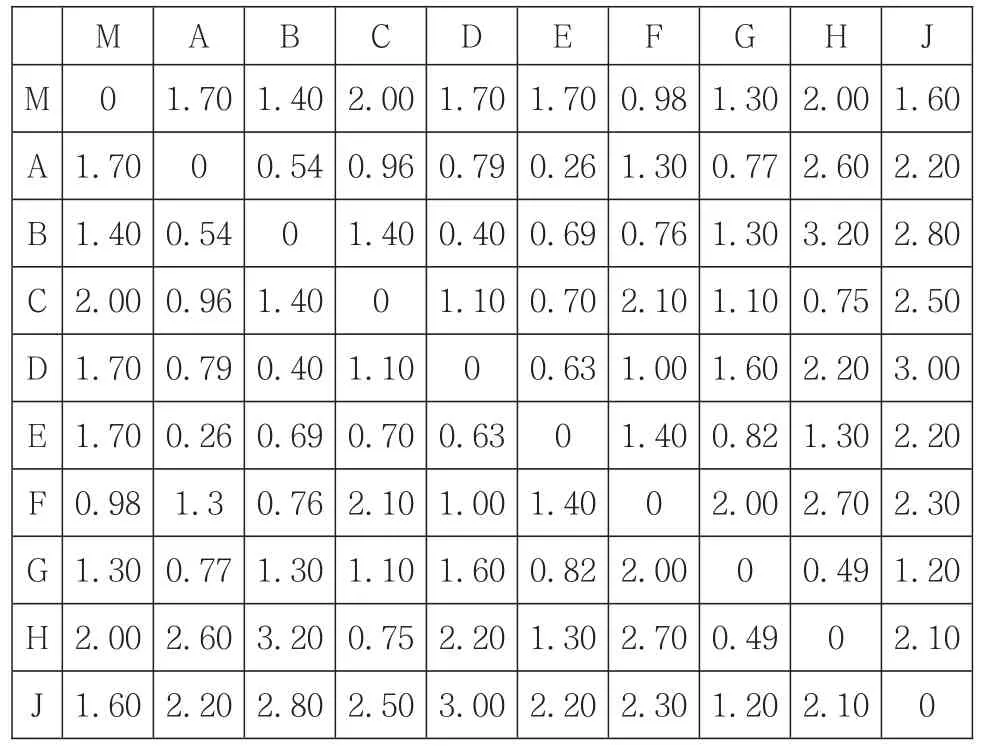
表3 配送中心与客户之间的距离矩阵

本模型主要是从路径最小化入手，根据客户的地理位置以及各个客户点之间的距离，在满足载重量以及车辆数目的前提下，利用MATLAB进行编程，模型采用遗传算法进行求解，最终得到优化路径，具体如图3所示。

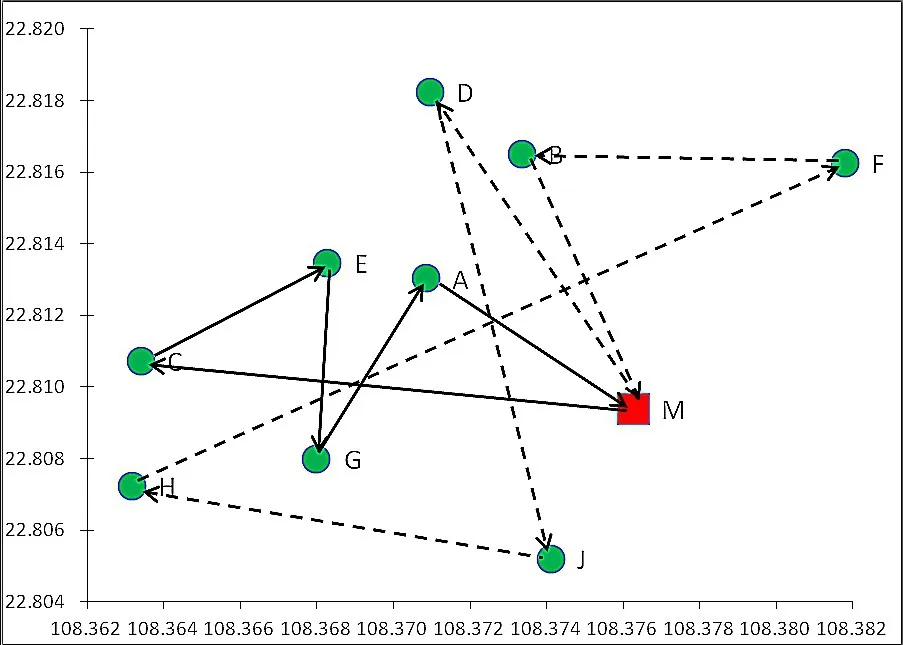
图3 遗传算法求得最优配送路线图

在最优的配送路径中，共选用两条路线对这9个客户（A—J）点进行配送，从上图可看出，车辆对客户的配送路线分别为：

第一条的配送路线：M—C—E—G—A—M，即配送中心M点部—南湖名都广场—和兴大夏—水产畜牧学校—琅西菜市—配送中心M点部；

第二条的配送路线：M—D—J—H—F—B—M，即配送中心M点部—铭湖经典—青湖中心—南宁三中—民歌湖—太平洋世纪广场—配送中心M点部。

在此方案中，其具体的配送量和配送路程如表4所示。

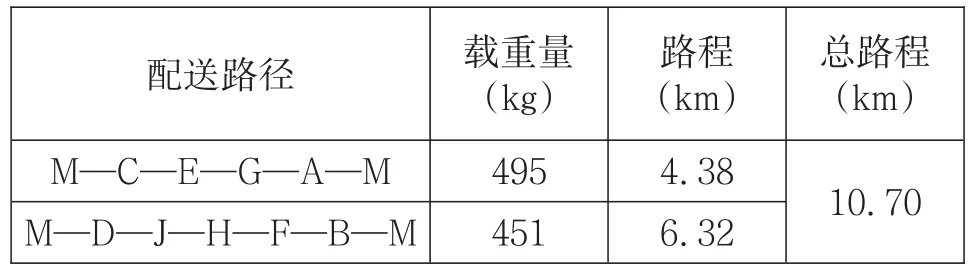
表4 最优方案的配送量以及路程

运用MATLAB软件得到遗传算法最优配送方案的最优适应度函数值随迭代次数的变化情况如图4所示。

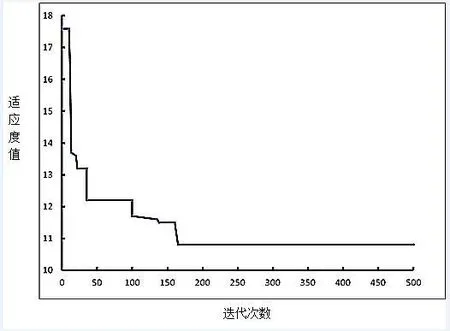
图4 适应度值随迭代次数的变化情况

从上图4可以看出，适应度值在迭代次数为160时，达到最优解。

（四）计算结果

结合具体的问题采用遗传算法在满足配送量以及车辆数目的情况下得出采用两条路线方案的最优配送路径，第一条的配送路径为：M—D—J—H—F—B—M，即配送中心M点部—南湖名都广场—和兴大夏—水产畜牧学校—琅西菜市—配送中心M点部，路程为4.38km，配送量为150kg；第二条的配送路径为：M—D—J—H—F—B—M，即配送中心M点部—铭湖经典—青湖中心—南宁三中—民歌湖—太平洋世纪广场—配送中心M点部，路程为6.32km，配送量为 134kg。两条路线的总路程为10.7km。

五、结 论

快递配送问题是一个多元化复杂问题，尤其在寻求经济效益与环境保护最优组合上，其末端配送占据着整个物流配送成本中的大部分。如今生鲜电商快速发展，越来越多的人们选择了线上下单线下取货的方式，由此带来的配送问题已不容忽视。借助云大数据、数学模型来优化配送线路已经是企业配送线路优化的发展趋势。文中采用MATLAB软件进行遗传算法的路径优化，也是基于以最低配送成本作为最终优化目标，考虑其配送成本与配送里程的关系，在结合实际情况忽略一些因素的情况下，将配送成本最低转换为以配送路程最小作为最终的优化目标。通过软件辅助计算得出M快递点部对9个客户点的最优配送路径为采用两条路线进行配送。另外在研究路径优化模型中的一些假设条件与约束条件可能会对最终结果造成一定的干扰，对研究的问题还不够完善，如何进一步降低配送成本还需要进行更加深入地研究。