基于GABP算法的油墨配色研究

张 阁，郑元林，廖开阳，刘梦莹，王晓彤

(1.西安理工大学 印刷包装与数字媒体学院，陕西西安710048； 2.陕西省印刷包装工程重点实验室，陕西西安710048)

在科技飞速发展的今天，精美的包装已逐渐成为大众消费的重要指标。为了使工业技术与信息化时代的发展步调一致，印刷行业的改革也势在必行，油墨配色作为印刷的核心已成为各企业竞争的关键。自印刷技术发展以来，主要以纽介堡方程[1]、Kubelka-Munk、蒙版方程、三刺激值、人工神经网络和光谱配色[2]理论为油墨配色[3]的研究对象，其中人工神经网络因具有处理复杂信息的能力而成为各学者研究的热点。人工神经网络是由大量的简单基本元件即神经元相互联接而成的自适应非线性动态系统，能够自身适应环境，总结规律，完成某种运算、识别或过程控制，具有较强的逼近非映射能力，但学习算法还需进一步完善。基于这些理论的缺陷，国内外学者不断地在提出新方法并加以改进。Zurita等[4]提出了利用Kubelka-Munk理论的二阶倒数的方法计算砂浆颜色浓度，平均误差达到8.80%，但在颜色浓度较高时测量精度降低；Furferi等[5]提出了Kubelka-Munk理论加人工神经网络的方法对织物进行配色，较Kubelka-Munk理论算法精度提高，平均误差减小；基于光谱匹配的油墨配色方法[6]减小了油墨厚度与光照的影响，但是该方法受设备影响较大；基于混纺纱线的分光光度颜色匹配算法[7]匹配的平均色差达到1.17%，具有实用性。目前，这些理论已成功应用到生产中。国外已经成功开发了基于Kubelka-Munk理论的配色软件，例如爱丽色公司的Color iMatch纺织品配色软件、Datacolor公司的Match-Pigment，这些软件通用性高，已被很多厂家使用，但是精度还可以进一步提高。基于以上配色算法的优缺点，本文应用遗传算法优化BP神经网络的模型来进行油墨配色。遗传算法是一种全局优化算法，可以优化配色模型中的参数，因此文中主要针对BP神经网络容易陷入局部最小这一缺点，利用遗传算法对其结构进行改进，找到最优参数进行网络训练，使输入值可以准确地映射到输出值，从而得到更精确的光谱配色方法，结果显示配色精度优于BP神经网络算法。

1 实验设计

1.1 实验数据采集

本文使用了《新编四色配色印艺图典》的色谱颜色样本作为训练和检验数据，色谱由胶印油墨(CMYK)印刷，其中分为四个部分：青品黄黑单色梯尺、二次色样本、三色样本、四色样本。单色梯尺由网点面积率从0到100%，间隔为10%(另外增加5%)的色块组成；二次色样本由黄品青黑四色两两组合叠印而成，每一色的网点面积率以10%为间隔从10%到100%；三色样本由CMY三色叠印而成，各色块网点面积率从10%到100%，间隔10%组成；四色样本由青品黄以网点面积率为10%的间隔，K以网点面积率为20%的间隔组成(K为90%时，C不包含90%、100%)；这四部分色谱分别叠印在铜版纸上，形成不同的色块，表1为色块组合。测量过程中使用X-Rite eXact在M1、D50、2°视场条件下测量了色谱的光谱数据和CMYK四色网点面积率，测量波长范围为400～700 nm，间隔10 nm取其色块的光谱值与CMYK四色网点面积率，总共测量有6 422组数据。为保证色谱测量的精确度，每个色块测量3次，然后取平均值作为最终结果。

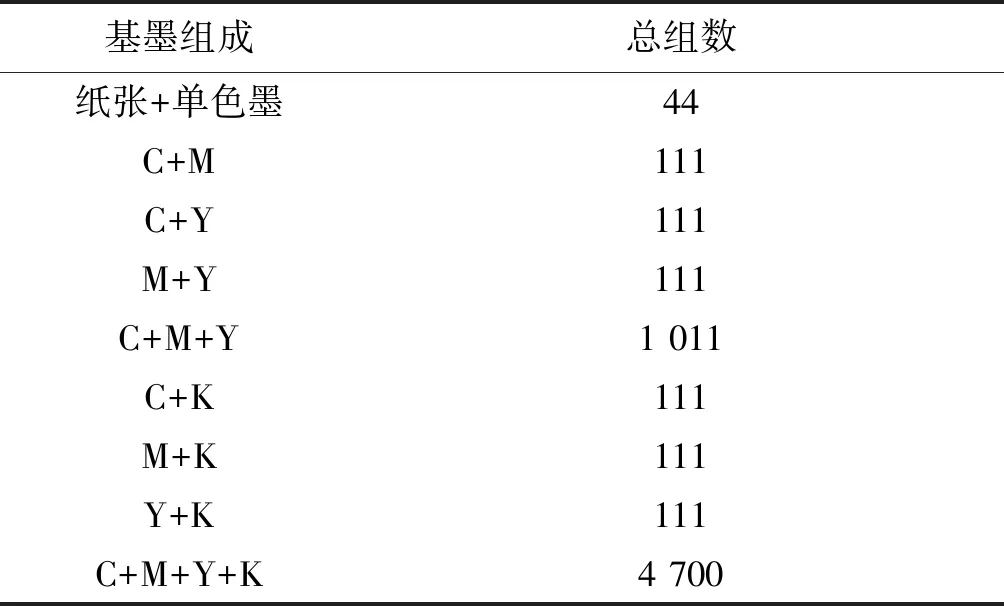
表1 色块组合

1.2 实验研究

该实验以BP神经网络为基础的输入数据通过非线性映射函数映射到高维特征空间，用于预测目标值CMYK的网点面积率。将测量色块的31维光谱值作为输入值, 输出为4维的CMYK网点面积率。实验测量数据随机选取5 600组光谱数据进行网络训练，822组数据进行验证。为检验网络的稳定性，实验进行50次，取平均值作为最终误差[8]。表2为部分原始光谱数据。

为了使所有数据在同一维度，网络训练前首先对原始光谱数据进行归一化，方便后续的数据处理，并且使网络训练速度更快。

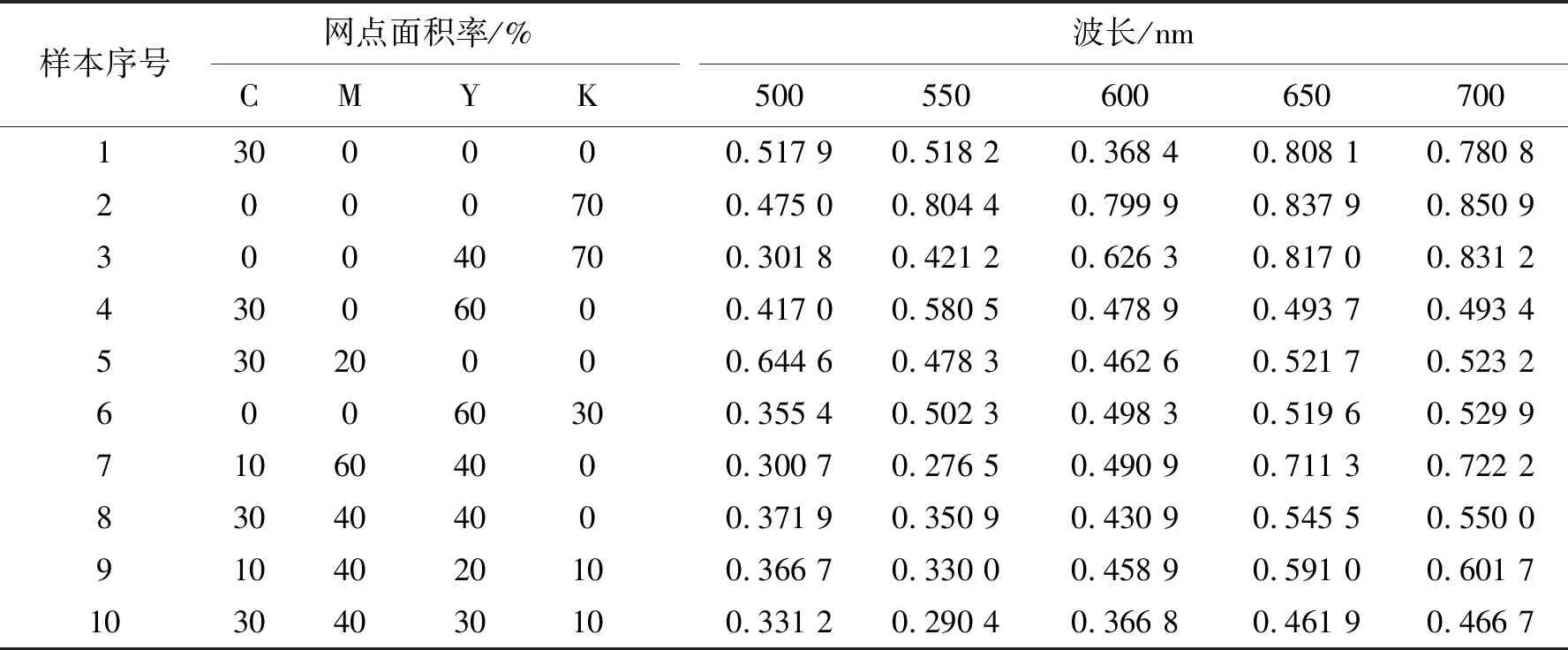
表2 部分光谱数据

2 构建预测模型

2.1 BP神经网络及结构设计

2.1.1神经网络

BP神经网络又称为误差反向传播神经网络，它是一种多层的前向型神经网络。在BP网络中，信号是前向传播的，而误差是反向传播的。

1) 前馈神经网络是一种非线性函数映射设备，用于确定非线性函数向量，输入数据向量P通过非线性映射函数f映射到高维特征空间，用于预测A。在这种架构中，P是一组M维输入向量，A是一组相应的N维输出向量。其中f为非线性映射函数，输入层节点的训练函数为trainlm，隐层节点的传递函数为tansing，输出层节点的传递函数为purelin。

P=[p1,p2,…,pM]T

(1)

A=[a1,a2,…,aN]T

(2)

非线性映射可以表示为：

A=f(P;W)+b

(3)

式中，W为权值集合；b为阈值集合。BP神经网络流程图如图1所示。

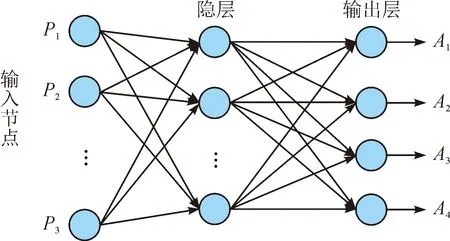
图1 BP神经网络流程图Fig.1 BP neural network flow chart

2) 反向传播训练过程目的在于修正权值，得到最优集合W。计算过程为：评估所有特定节点的输入加权和，然后使用非线性映射函数f对隐层和输出层进行转换，计算输出节点的输出值与其目标值的均方误差，最终更新权重集合W。

2.1.2神经网络参数确定

1) 神经网络节点数的确定

输入层的节点为31，输出层的节点为4，结合网络训练速度和目标精度并经多次验证，文中选用单隐层结构，隐层节点为30。

2) 神经网络训练

训练参数包含迭代次数、学习速率、目标精度和动量因子这几个部分。学习速率有不断调整权值和阈值的作用，根据多次实验将值设为0.1，为了避免神经网络陷入局部最小，文中添加了动量因子，设置为0.005。迭代次数为1 000，目标精度为0.000 01，网络训练过程[9]中达到目标精度则停止训练。最终输出结果循环50次后取平均值。

BP神经网络训练流程为：

步骤一 对样本进行归一化处理，所有数据归一化到[-1,1]之间；

步骤二 两组实验分别取样本进行网络训练，结果达到目标精度时停止训练；

步骤三 选取测试样本进行网络测试，最后进行误差分析。

2.1.3BP神经网络预测结果

根据建立好的BP神经网络，使用822组测试样本进行仿真训练，图2为测量值与预测值的误差分布直方图。

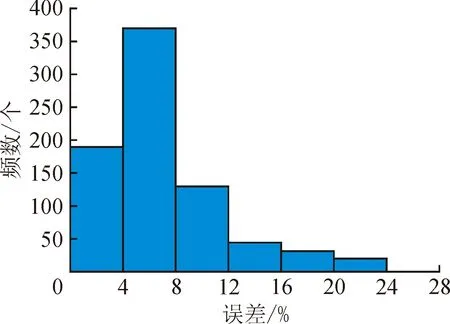
图2 BP神经网络的误差分布直方图Fig.2 Error distribution histogram of BP neural network

从图中可以看出，822组测试数据经过BP神经网络计算，误差集中分布在[0.04,0.08]，平均误差为8.6%。从该实验可以看出，仅使用BP神经网络误差较大，说明该结构需要进一步优化。

2.2 遗传算法及参数设置

遗传算法抽象于生物体的进化过程，通过全面模拟自然选择和遗传机制，形成一种具有“生成+检验”特征的搜索算法，它在整个进化过程中的遗传操作是随机性的，但它所呈现出的特性并不是完全随机搜索，它能有效地利用历史信息来推测下一代性能有所提高的寻优点集。物种不断进化，最后收敛到一个最适应环境的个体上，求得问题的最优解。

遗传算法以编码空间代替问题的参数空间，以适应度函数为评价依据，以编码群体为进化基础进行遗传操作建立起一个迭代过程。遗传算法的优越性主要表现在不容易陷入局部最优，即使在所定义的适应度函数不连续、非规则或有噪声的情况下，也能很大概率地找到整体最优解。遗传算法所涉及的五大要素包括：参数编码、初始群体的设定、适应度函数的设计、遗传操作的设计和参数的设定。

1) 实数编码

样本数据输入后，首先随机产生权值和阈值并对其编码产生一定数量的染色体。遗传算法中常用二进制编码，因为它的通用性高、使用方便，所以经常被用于编码。二进制编码的进化层次是基因，实数编码的进化层次是个体。在参数变量范围较大的模型中，若采用二进制编码，其编码字符串长度太大，使得染色体的编码和解码占用计算机时间较长，另外，二进制编码的杂交和变异对动力学模型的参数估计问题缺乏明确的物理意义。文中举例参数A的两种编码方式，图3中左图为参数A的二进制编码，右图为参数A的实数编码形式)。相比之下，实数编码[10]不仅无需转换数制和数据类型便于理解，而且节省遗传操作时间。另外，实数编码具有精度高、便于大空间搜索的优点。

图3 编码Fig.3 Coding

2) 初始化种群

初始化种群开始阶段，生成一定规模的种群并同时开始进化，每个种群都由待优化参数(权值和阈值)编码而成的染色体组成。遗传算法进行时随机产生40个种群并开始进化，进化代数为20，进化开始后每一代染色体和其位置都会被记录，方便以后的最优染色体杂交变异。

3) 适应度计算

在遗传算法中[11,12]，采用适应度函数来区分群体中个体的好坏，以及评价测试样本的输出值和期望值之间的误差。计算过程为先对染色体进行解码，然后用设计的模型进行网络训练，这时的权值和阈值为优化之后得到的值，输入向量P(光谱值)将会对应输出向量A(与光谱值对应的四色网点面积率)，最终用适应度函数[13]验证其性能。在计算当中，MSE充当适应度值，并根据性能目标进行最小化。i表示输入节点数(I为实验中用到的光谱数组总数)，k表示输出节点数(K为四色网点面积率输出数组总数)，ti，k和si，k分别表示第i个输入样本下第k个输出样本的预测值和期望值。

(4)

式中，P、A分别为向量P、A的数值。

4) 杂交与变异

杂交的作用在于将优良的基因传给下一代个体，并生成包含更复杂基因结构的新个体。这个过程主要是在交配池中随机选取一对染色体，并随机选取杂交位置根据杂交概率Pc相互交换各自的部分内容，从而形成一对新的个体。变异是通过变异概率Pm随机反转等位基因来实现的。

为提高遗传算法求解效率，本文将寻找Pc和Pm的最优组合，判断的准则为找到最优参数所需要的遗传代数最少。Pc限定在[0.7,1.0]范围内，Pm限定在[0.003,0.05]范围内，固定某一Pc值，改变Pm值进行运算，从而找到最优组合(Pc，Pm)。最终确定Pc为0.7，Pm为0.004。

5) 最优种群

在各种群进化过程中会将进化最好的个体选择出来放在最优种群中，最终以进化代数作为终止的依据。图4为混合模型训练流程图。

图4 混合模型(GABP)流程图Fig.4 Framework of the proposed GABP method

3 混合模型在配色系统中的应用

本小节对图5油墨配色流程图进行说明。

1) 构建模型。对四色墨进行其光谱值与CMYK不同网点百分比的测量，并输入油墨配色系统建立一个完整的配色系统。这些数据将作为标准值来完成不同客户的印刷需求。

2) 配方计算。首先测量待配色样品的光谱值，将光谱值所有的数据输入配色系统，系统开始计算，所有数据归一化处理，系统根据输入数据随机产生权值和阈值，遗传算法生成一定数量的种群开始进化，反复繁殖找到最优参数并赋予BP神经网络训练，网络会根据输入值进行迭代计算，直到找到与之对应的误差最小的一组四色网点面积率，计算停止。

3) 模型应用。最终按照上一步计算的CMYK四色网点面积率，直接调配四色墨进行印刷[14]。

图5 油墨配色流程图Fig.5 Framework of the proposed ink color matching method

传统印刷工艺主要依靠工人凭借经验给出印刷配方，该方法对工人技术有太大的依赖性，容易造成油墨、承印物的浪费。GABP模型的应用不仅能够稳定预测出所需油墨的网点面积率，而且还有效防止了材料的浪费，将为企业提供一种更便利的生产方式。

4 数据分析

将样本数据输入GABP模型进行计算，重复50次并选取平均误差作为最终结果。

1) 在遗传算法计算适应度时，MSE充当适应度值，将目标进行最小化。图6为样本训练后的适应度曲线，在进化代数为5时，适应度达到最佳值为227，说明此时染色体在进化过程中达到最佳状态。

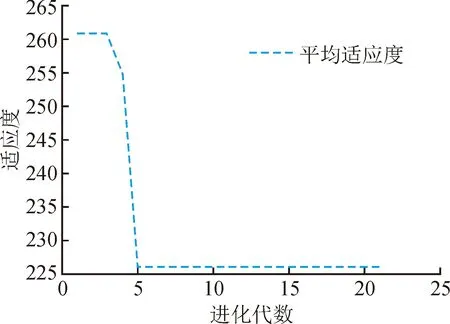
图6 适应度曲线图Fig.6 Fitness curve

2) 最优种群得到后，网络中各参数确定并同时进行网络训练。网络运行结果如图7所示，蓝绿红曲线分别为训练值、验证值和测试值，图中绿色圆圈处代表实验经过97次迭代，最终达到最佳精度并停止工作。在迭代次数为97时，最佳验证性能为0.004 619 1。

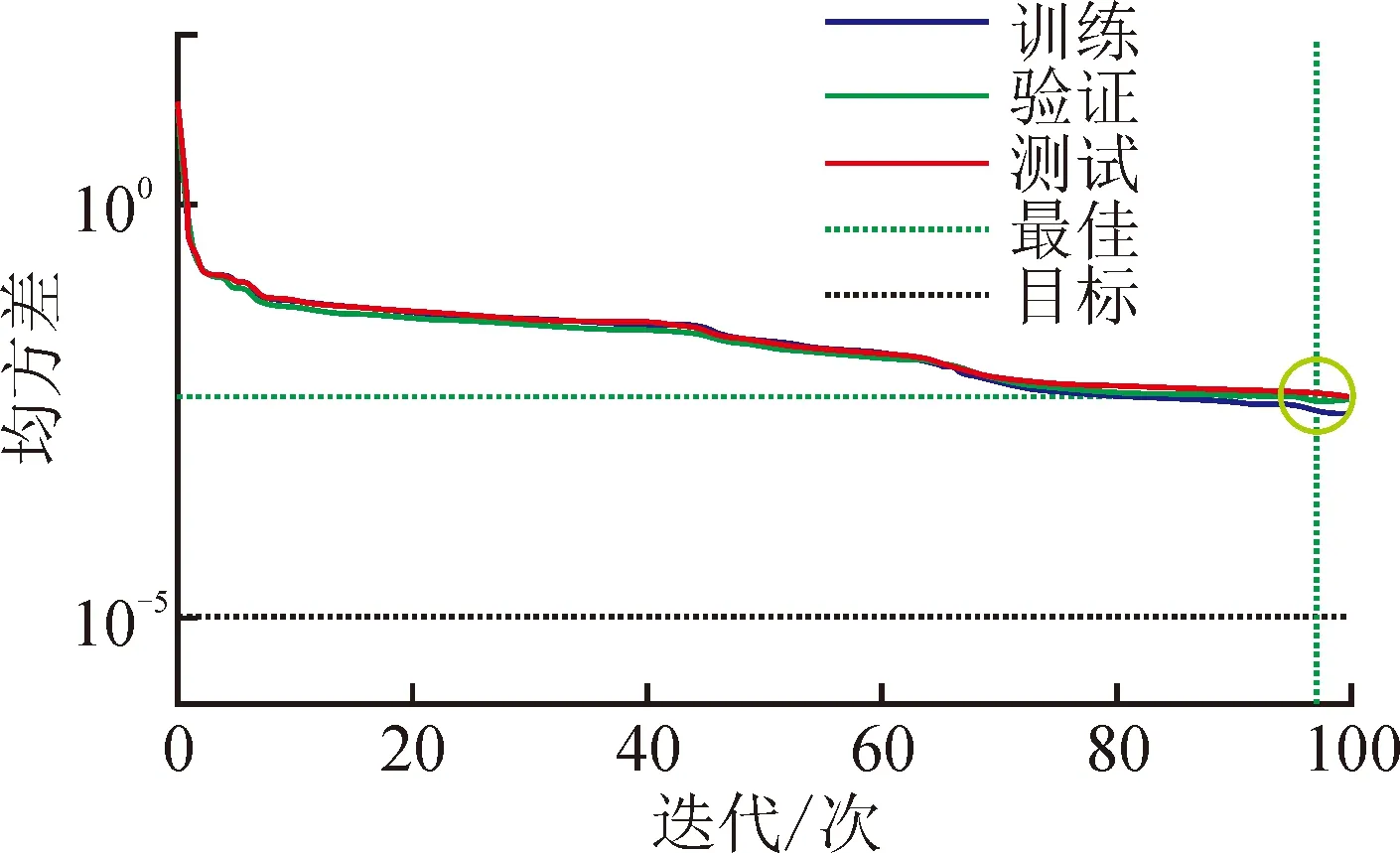
图7 神经网络学习曲线图Fig.7 Neural network learning curve

3) 总结实验结果可得到实验误差直方图，如图8所示，其中横坐标为误差范围，纵坐标为误差频数。图中表明了在实验中每组数据的CMYK四色网点面积率测量值与预测值误差分布的情况，其中误差主要分布在[0,0.08]内，822组数据经过BP神经网络测试平均误差为4.5%。

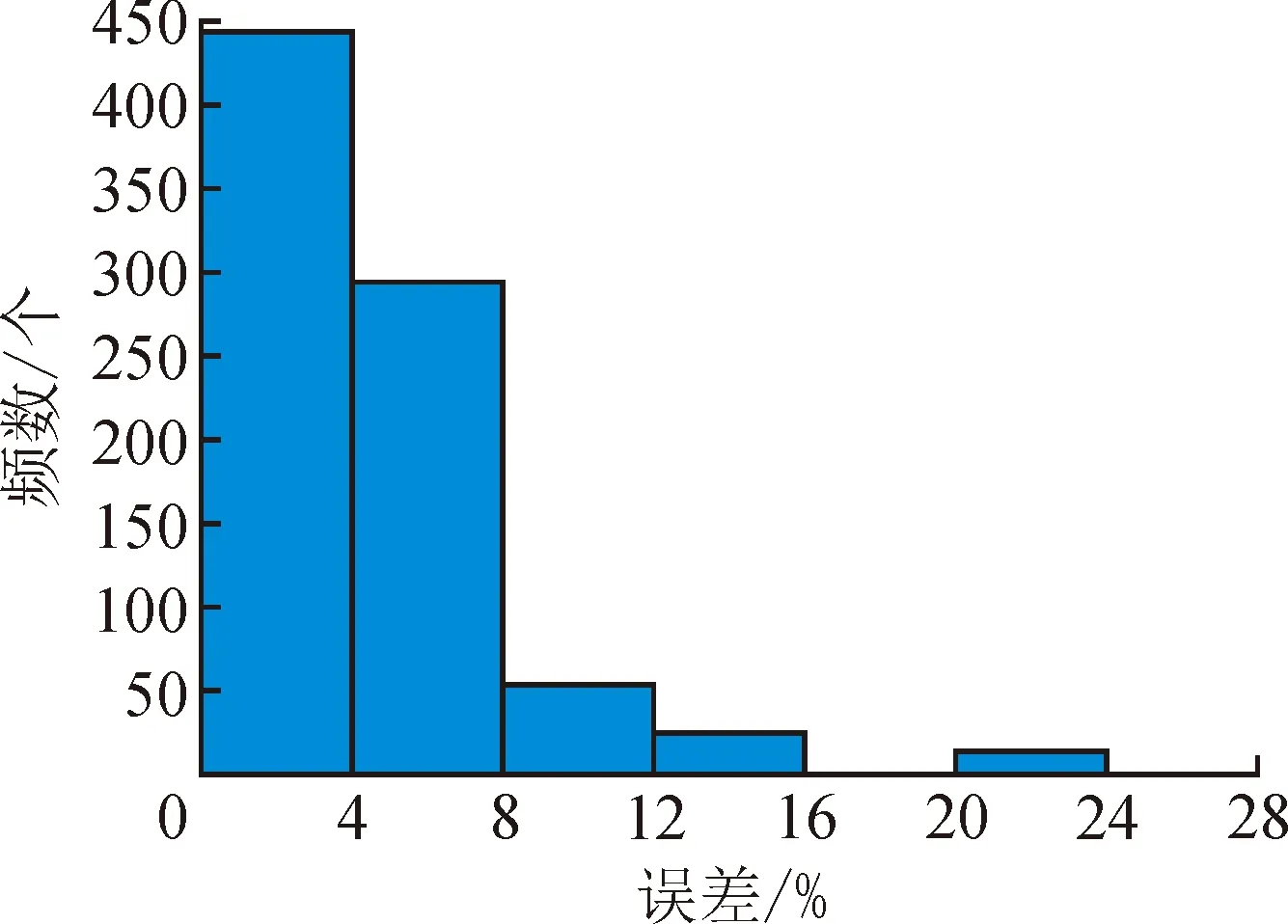
图8 GABP误差分布直方图Fig.8 Error distribution histogram of GABP

4) 网络训练结束后仿真得到的预测值经过反归一化处理得到最终结果。文中截取10组随机取值的输出数据进行误差对比分析，表3为CMYK混色的实际测量值与预测值的均方误差。

通过对表中数据进行误差分析可以直观地看到，CMYK四色网点面积率测量值与预测值十分接近，误差较小。实验表明，经过遗传算法优化的BP神经网络训练能力较好，较BP神经网络误差明显减小。

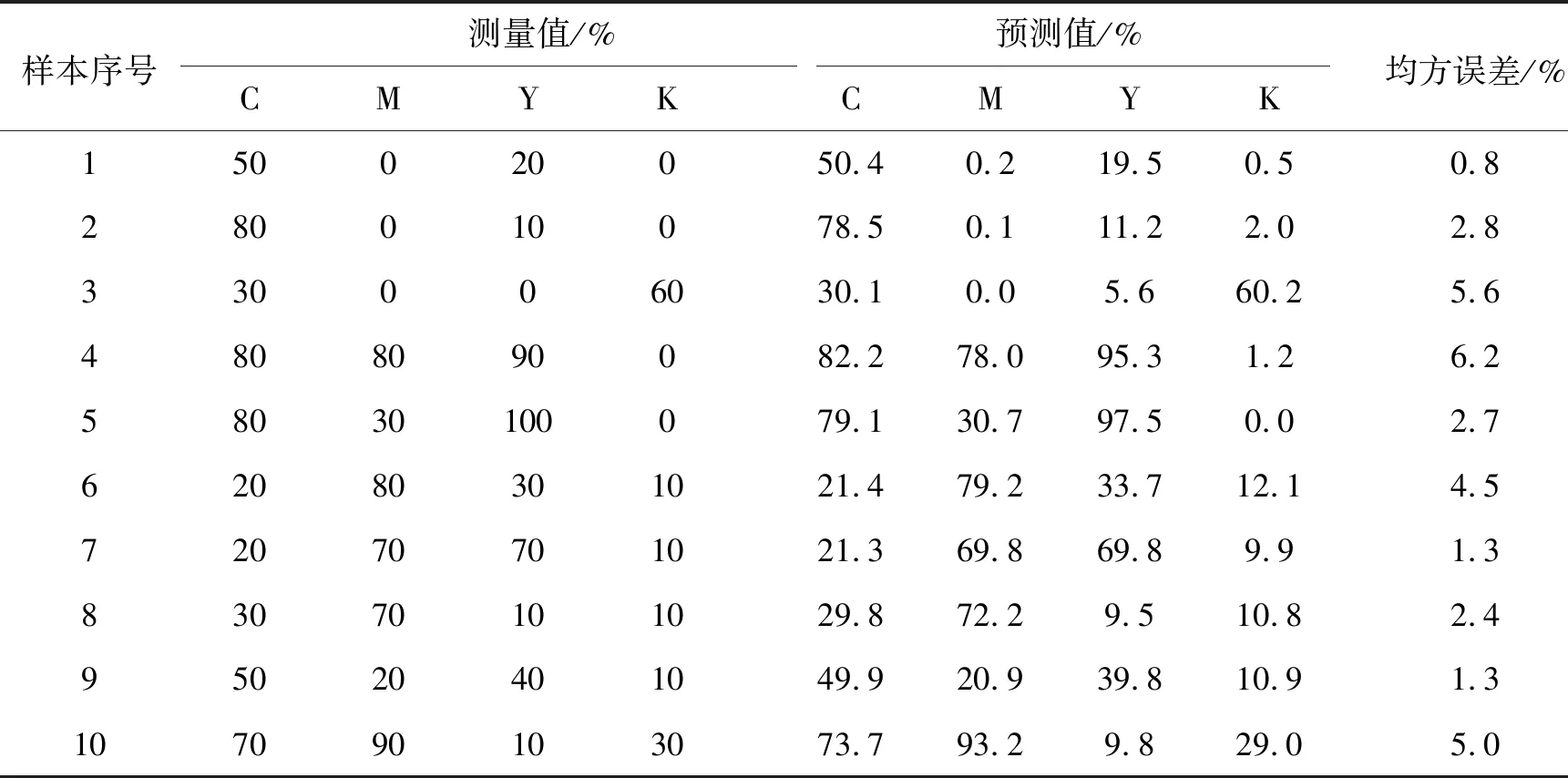
表3 预测值与测量值的误差分析

5 结 语

为了找到最佳配色系统，本文通过创建GABP混合模型来实现光谱配色，利用构建的模型使光谱反射率找到与目标值CMYK最接近的值与之匹配。文中通过样本数据随机选取的方式进行实验，平均误差为4.5%，在实验过程中网络收敛速度较快，计算结果的精度也比较好，说明经过改进的BP神经网络能够弥补结构上的不足从而找到最优参数，并能进一步训练得到准确的目标值。同时也说明经遗传算法优化改进的BP神经网络具有良好的非线性映射能力，泛化能力高。在配色系统中模型的建立是至关重要的，它决定了系统是否能够准确的印刷出满足客户需求的样品。实验证明，应用GABP油墨配色系统配色精度较高，能为印刷企业提供较为准确的配色方法。