一种光学探测海底粗糙度的算法及其实验研究

高荪培，徐 剑，邹 博

(天津大学 海洋科学与技术学院，天津 300072)

引言

海底沉积物的特性，对于军用反潜作战、智能化武器的发展、探测水雷，以及民用上的海洋工程选址、海底资源开发都起到重要作用。其中海底微地形粗糙度是海底沉积物性质中的重要参数。因此，研究海底粗糙度的表达和探测有着重要意义。由于海底沉积物往往具有松散颗粒的结构特点[1]，打捞后原始结构会遭到影响，所以多采用近距离、原位观测海底微地形粗糙度的技术方法。

海底微地形粗糙度的测量随着上世纪七十年代海底声散射研究的开始而兴起。作为传统的测量方法，手工测量和电导率探针方法属于接触式测量，这种方式存在分辨率低、准确度差的问题。1978年，Akal和Hovem作为早期的研究人员，曾使用立体摄影测量法统计和量化海底微地形[2]，基于多个不同角度的水下照片对摄像机进行校准，以获得海底三维数字高程模型[3]。但是这种方法成像时需要校准，实现复杂，并由于海洋复杂的环境中难以实施单一位置多镜头复现的问题，导致该方法在实际应用中难以开展。十九世纪以来，测量海底底质粗糙度参数的方法得到极大发展，2016年，Isakson提出了一种移动式激光测量方法，将激光测量装置安装在ROV(remote operated vehicle)上，可以在无需海底设施的条件下实现大面积测量，并于佛罗里达部署实验[4]。

作为三维重建方法——SFS算法，成像时不需要校准，且可以通过单张照片中的亮度信息得到海底微地形的数据。SFS算法目前也已经发展了多种理论和应用，并被应用于地形观测、缺陷检测、人体建模等[5-6]。然而，其水下光学应用相对较少。本文将SFS算法拓展到水下，并通过该方法表示三维海底微地形，提取粗糙度参数。

1 理论模型

1.1 微地形测量

工件表面粗糙度是一个重要的参数[7-8]，而海底微地形粗糙度对于声纳的性能也具有不可忽视的影响。获取海底微地形的数字表示是计算粗糙度参数的第一步。用函数z(x,y)来描述海底微地形成像结果，x、y对应于二维成像中的横纵坐标，z是像素点(x,y)对应的真实海底点的相对高度，也就是需要求解的变量。具有亮度I(x,y)的图像中的每个点p(x,y,z)对应于真实海底中的点P(X,Y,Z)。考虑到海水对光线具有强吸收、散射作用，依据光学规律建立光线传播模型，如图1所示。

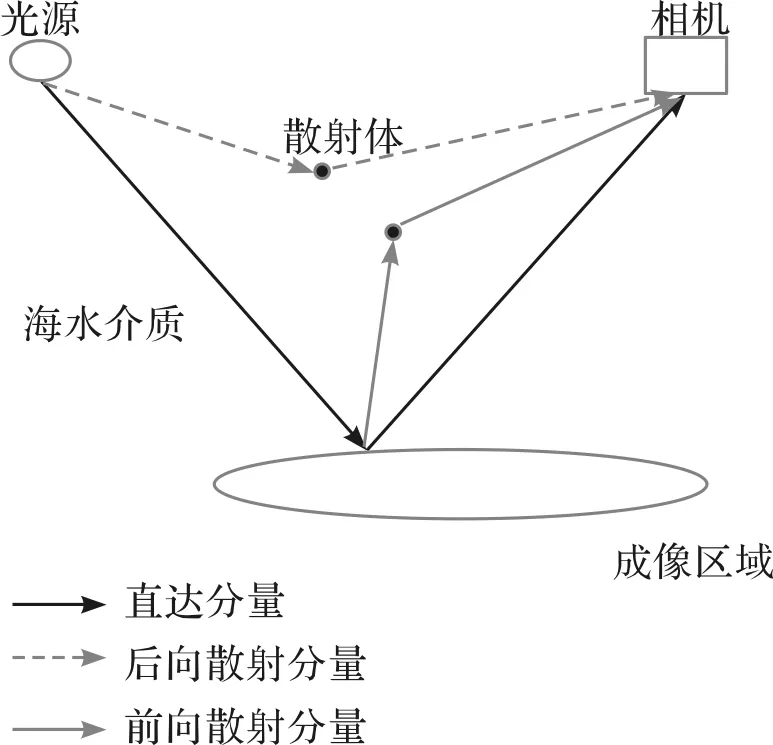
图1 水下光传播路径Fig.1 Underwater light propagation

根据Beers法则，水下光吸收的规律符合[9]：

B=B0e-αd

(1)

其中:B0代表发射光强度;d是通过介质传播的距离;B是光线在水中经过d距离后的光强;参数α是介质中的光吸收系数。通常，吸收系数以cm-1为单位。考虑到上述海水对光的吸收、散射等物理现象，在假设透视投影的情况下，根据Shaomin Zhang的理论，水下散射规律可写为[10]

(2)

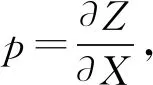
(3)

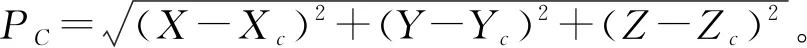
(4)

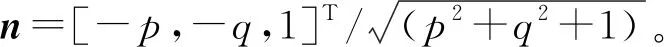
(5)

代入方程(3)，有：

(6)

IW(x,y)为水下照片里各像素点的归一化亮度，方程(6)是一个含有p、q两个未知数的方程。在不添加约束的情况下，这是一个病态方程，因此需要对方程添加约束才能进行求解。Horn加入了平滑、可积和强度约束，将方程转换为功能极值的解；Zheng和Chellappa用图像梯度代替了平滑的约束条件，用函数极值的方法求解该方程[12-13]。 Tsai引入了牛顿迭代法[14]，离散化之后，梯度p和q为

p(x,y)=z(x+1,y)-z(x,y)

(7)

q(x,y)=z(x,y+1)-z(x,y)

(8)

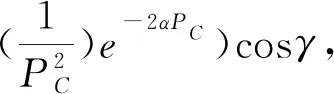
f(z(x,y),z(x+1,y),z(x,y+1) )=IW(x,y)-

Gr(p,q)=0

(9)

将k设置为迭代次数，对上式在z(x,y)=zk-1(x,y)处进行泰勒展开，并进行一阶近似，我们可以得到：

f(z(x,y) )≈f(zk-1(x,y))+(z(x,y)-

(10)

一阶展开后，(9)式可由(11)式近似：

(11)

其中fz是z(i,j)的导数：

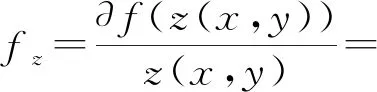
(12)

经过迭代后，进行标定，即可得到微地形的三维数字模型。

1.2 粗糙度求解

经过上一节求解，可以得到水下微地形。测量时水下装置配置如图2所示，将摄像机放置于待测区域上方的ROV或水下框架上操作。待测参数包括从相机到该区域中心的距离以及光吸收系数。

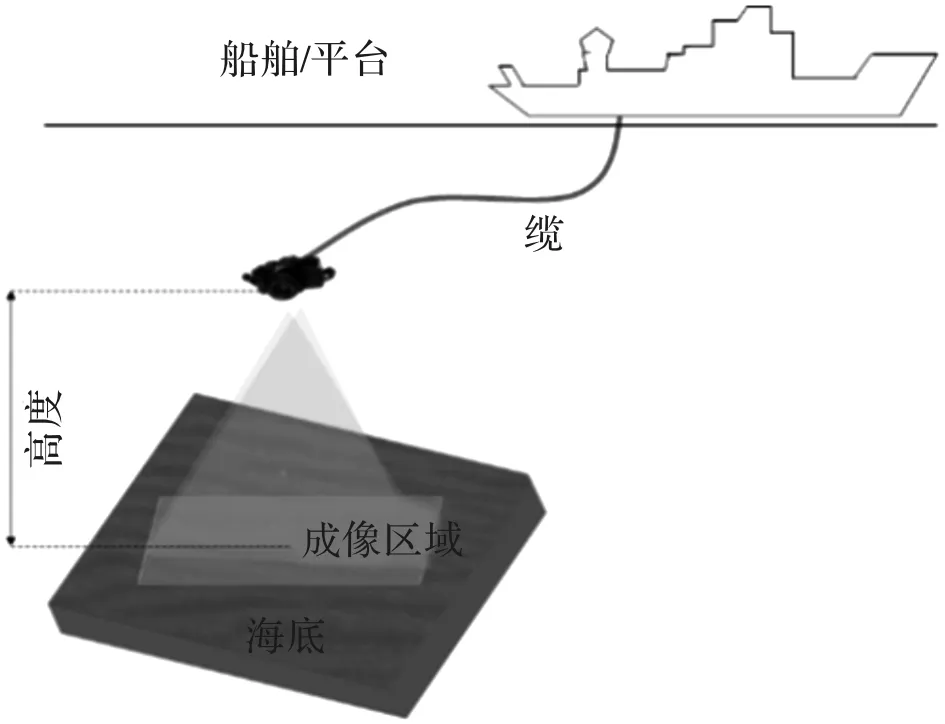
图2 水下装置配置示意图Fig.2 Underwater installation schematic

成像结果如图3(a)所示，成像范围为0.4 m×0.4 m，经过三次迭代后，获得的数字高程模型(digital elevation model,DEM)如图3(b)所示。

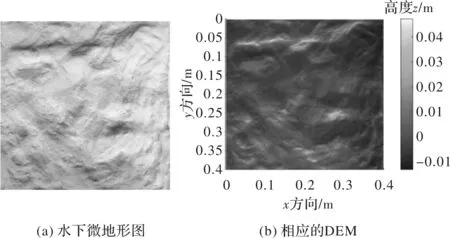
图3 图像及其DEMFig.3 Underwater micro-topography image and its DEM

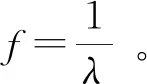
(13)

海底粗糙度的功率谱强度近似符合幂律形式，因此可以表示为

(14)

其中：W(K)是粗糙度谱；K表示二维波长向量；参数ω2称为谱强度；参数γ2称为谱指数。用B(R)表示高程数字信息的协方差函数。根据Wiener-Khinchin定理，粗糙度谱W(K)可以由B(R)的傅里叶变换求解得到：

(15)

设H(Kx,Ky)为微地形的频谱，z=f(R)在采样数为m/n的x/y方向采样，采样间隔为lx/ly，有：

(16)

在估算其粗糙度谱之前，为减少频谱泄漏，将二维Hamming窗应用于高度场数据，高度频谱强度等级以dB表示。

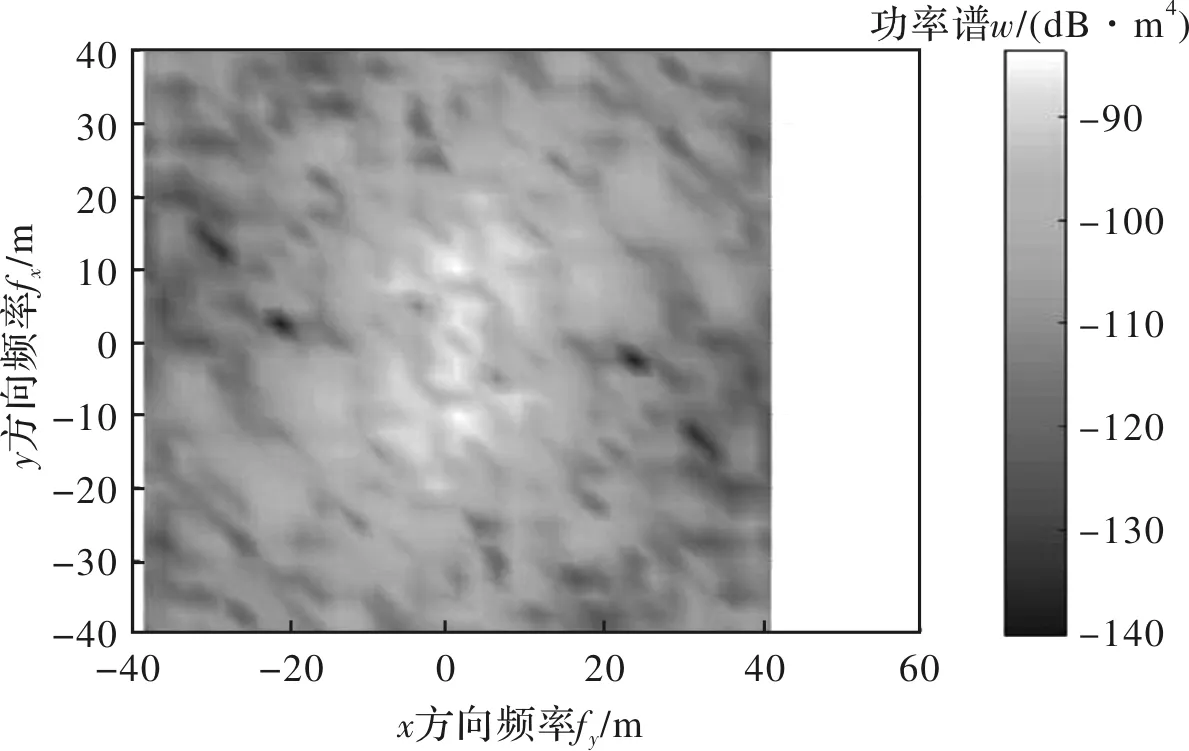
图4 计算得到的功率谱密度Fig.4 Cabculated2-D power spectra density

对海底粗糙度功率谱进行幂律拟合，结果如图5所示，其中W(K)和K以对数形式进行表示。拟合结果为γ2=2.581，ω2=10-4.768m4-γ2，置信度为95%。

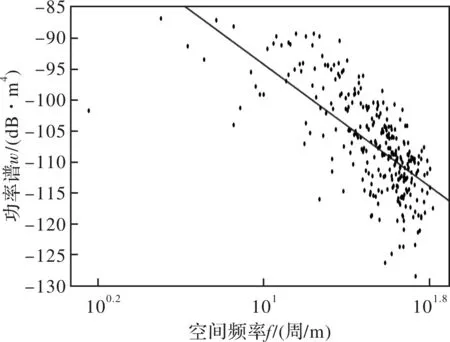
图5 拟合后的功率谱强度Fig.5 Roughness power spectra intensity after fitting

2 实验验证

验证实验于2017年在青岛市即墨海域附近部署，其海图位置与海底拍摄情况如图6所示。

图6 即墨附近水域海图及典型海底沙坡地形Fig.6 Nautical chart near Jimo and seabed ripples diagram

利用三角架架设水下相机，对海底沙坡进行成像，得到图7(a)中拍摄结果和图7(b)处理结果。将原始波纹图像与其功率谱强度进行比较，二维功率谱强度在空间频率域内具有整体倾斜的特点，如图7(b)所示，对应着图7(a)中沙坡的分布方向。根据图8中拟合的结果，观察得到粗糙度参数主要是由较高空间频率部分，即微地形的小尺度起伏决定的。对海底微地形的粗糙度功率谱数据进行幂律拟合，γ2=1.404,ω2=10-8.295m4-γ2，具有95%的置信度。所得的结果和Briggs在美国东南海岸测量海底粗糙度的结果相当[15]。如图9所示，水下SFS算法是一种有效的海底粗糙度测量算法。与Ispkson提出的方法相比，本方法更加便捷、价格低廉。

图7 海底沙坡及其对应的功率谱强度Fig.7 Simulated seabed ripples and its power spectrum intensity

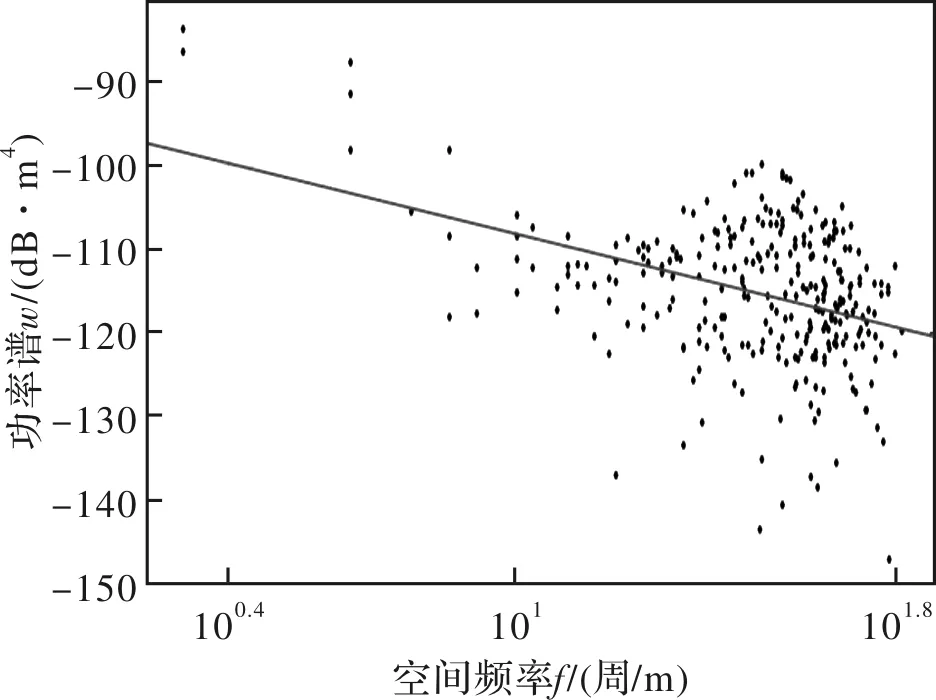
图8 拟合后的功率谱强度Fig.8 Roughness power spectra intensity after fitting

图9 手工测量和立体相机测量方法Fig.9 Manual and stereo camera measurement methods

3 结论

本文提出一种基于SFS的光学海底微地形粗糙度测量方法，结合水下光传播的特点，利用水下SFS得到海底微地形的数字高程模型进行仿真，并在即墨海域部署实验进行验证，证明了该算法有效性。该方法可以通过单张水下照片获得海底微地形特征。对于动态海底而言，这种可安装在ROV或框架上的光学系统非常有效，并且有利于长期和大面积观测。