非平行光干涉照明显微镜三维形貌检测研究
2019-05-24屈玉福
潘 晖,屈玉福
(北京航空航天大学 仪器科学与光电工程学院,北京 100083)
引言
机械制造和电子工业领域的快速发展,对微观形貌的检测技术提出了更高的要求。目前对三维形貌的检测可分为两大类:接触式和非接触式[1]。接触式的方法主要指触针法,其原理是将触针垂直方向的微小位移转换成电信号并加以放大,从而得到探测面的三维形貌分布。非接触式的检测方法主要包括光束聚焦法、结构光投影法和干涉法。光束聚焦法将聚焦后的光点当作光学探针,对探测表面进行扫描得到三维数据,该方法可对复杂轮廓进行三维检测,但测量速度较慢[2-4]。干涉法和结构光投影法通过解算条纹形变来检测表面轮廓,其中干涉法使用光纤相干或平行光束相干原理,包括激光干涉法[5-7]和白光扫描干涉法[8-15]。当使用光纤相干时,需配合较大工作距离的物镜,从而限制了物镜的放大倍数[7]。白光扫描干涉法使用宽光谱白光作为照明光源,使用平行光束相干的原理,单次测量误差在20 nm以内[10,12-13],不过,该方法需要使用干涉物镜产生条纹,并搭配轴向扫描装置调节条纹相位,结合条纹对比度和光强等信息确定被测表面的绝对深度[13]。结构光投影法避免了扫描装置的使用,重建速度最快,但当投影平面与载物台平面存在夹角时,需要对条纹周期进行修正,故该方法不适用于亚微米级精度的形貌测量[16-17]。
本文将结构光投影法与平行光干涉法的优点相结合,通过空间光调制器对光束进行衍射,使用2束光强接近的衍射级进行干涉来产生条纹,并通过改变上传的条纹图案精确调节条纹相位。由于避免了扫描装置和参考平面的使用,所提出的方法不需要使用干涉物镜,且对所使用物镜的数值孔径没有限制,重建过程速度快,并且可以达到更高的横向分辨率。此外,由于条纹由光束干涉产生,相位随着像素坐标线性分布,不会出现投影法中条纹周期变化的现象。最后本文以Ra为100 nm的粗糙度对比模块为被测样品进行了实验,使用四步相移法得到被测样品表面三维点云,依据被测样品表面各点的相位变化值得到三维轮廓上各点之间的真实相对高度。本文将从实验光路、重建算法、数学模型、标定方法、实验结果及精度分析6个部分对该方法进行介绍。
1 实验光路
图1为本文所提出非平行光干涉照明显微镜的光路图。激光经扩束镜L3、空间光调制器和调焦透镜L2射入显微镜的分光棱镜,构成显微系统的照明光路。空间光调制器可依据上传的图像对入射光进行振幅调制,当所上传的图像为条纹时,其作用相当于反射光栅,调节空间光调制器的偏转,让光强相近的2束衍射光射入分光棱镜,再经过显微物镜聚焦后干涉于被测样品表面,形成干涉条纹。
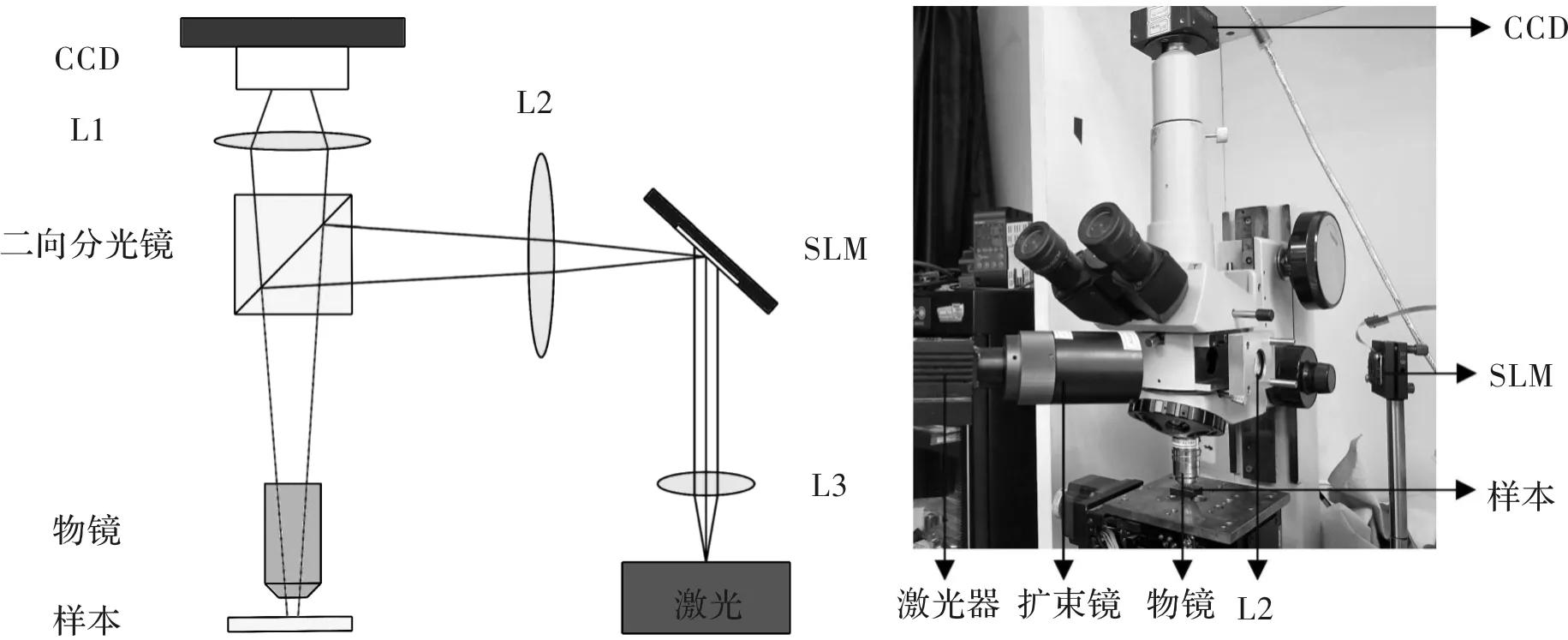
图1 非平行光干涉照明显微镜光路Fig.1 Optical setup using interference illumination of non-parallel light
空间光调制器是系统的核心器件,实验时可以通过改变上传的条纹图案精确调制条纹的周期和相位[18]。通常情况下,为提升三维重建点云的横向精度,需调节条纹周期,使其接近显微镜的横向分辨率,此时双光束的最大干涉角φ可由物镜的数值孔径NA计算得到。
φ=2arcsin(NA)
(1)
根据系统所使用显微物镜的参数(100×,NA=0.8),双光束的最大干涉角为106°,由瑞利判据计算得到的系统分辨率为406 nm。实验中,可调节得到的最小条纹周期为452 nm,说明在一个条纹周期内,至少存在一个像素点的相移与高度存在对应关系,即重建点云横向精度为452 nm,接近系统成像分辨率。由于条纹周期较小,条纹的形变相较于大周期的条纹更为灵敏,因此具有较高的轴向精度。在相位调节方面,白光扫描干涉法需借助压电装置在轴向移动干涉物镜,之后通过标定各扫描图像上的零光程差对相位进行拟合,故其相位值存在一定误差。在我们的系统中,相位调节通过空间光调制器控制其上像素实现,无需扫描装置,故具有更高的相位调节精度,在此基础上使用相移法计算图像上各点的相位调制值,可在较快的重建算法下得到高横向分辨率的三维重建结果。
上传条纹图案及干涉条纹横截面上像素的灰度值分布如图2所示。
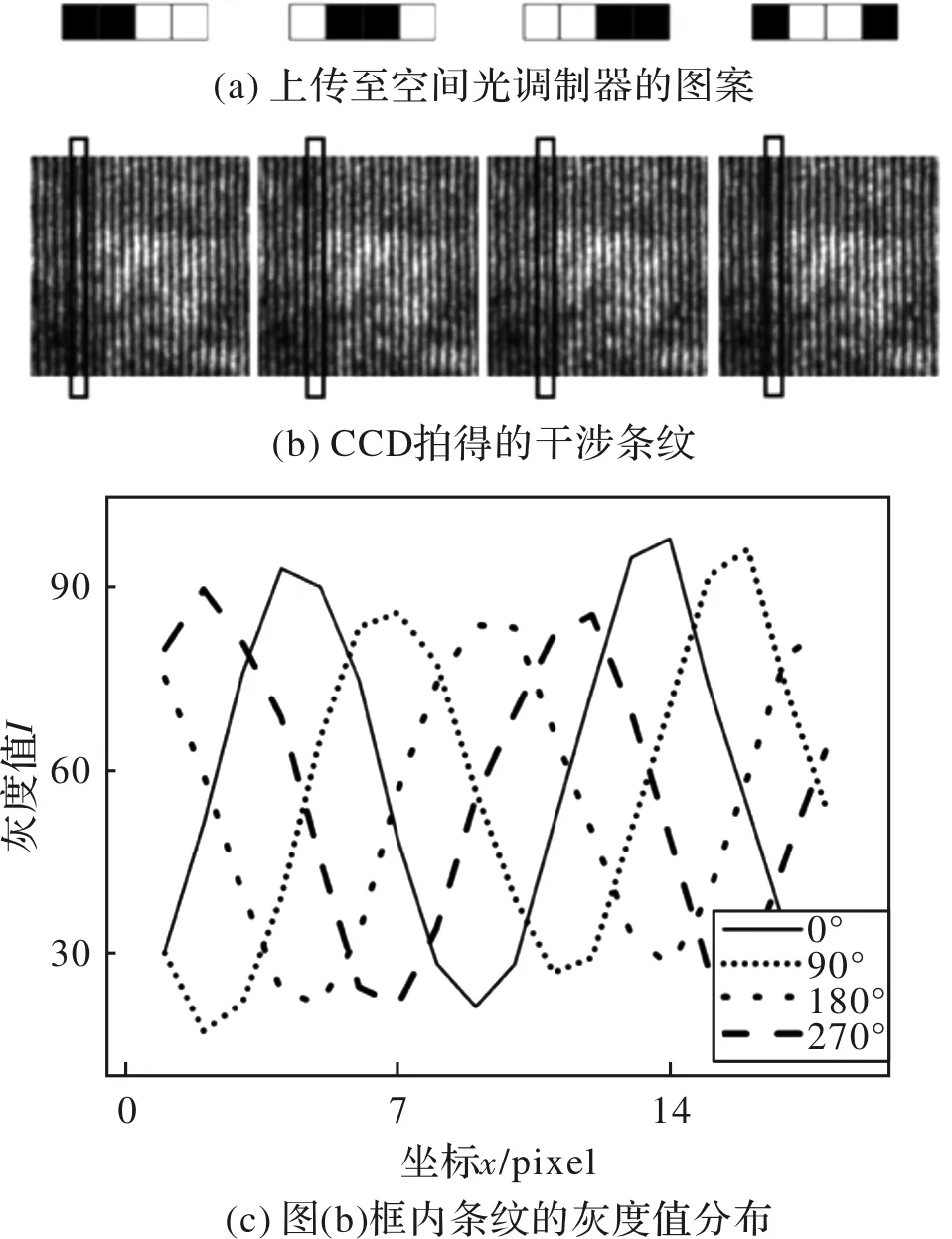
图2 等相位差的干涉条纹Fig.2 Interference fringes with equal phase difference
由图2(c)可知,条纹相位可精确调节,由于条纹周期为452 nm,故相位横向调节精度为113 nm。
2 重建算法
本文使用四步相移法对被测样品轮廓进行三维重建,分为图像预处理、提取相位调制图、噪声点滤除三步。下文将以Ra=100 nm的粗糙度对比模块为样本,对各步骤使用的算法进行说明。
2.1 图像预处理
由于成像系统使用激光照明,激光散斑对干涉图案的影响不可避免。在对干涉条纹进行预处理的过程中,本文使用椭圆形低通滤波[19],使得图像频域上沿条纹方向上的滤波半径为条纹垂直方向上的2倍。条纹图案在频域上表现为中心对称的2个亮点,2点连线方向垂直于条纹方向,将该连线所在方向设置为椭圆的长轴。由于条纹周期接近图像分辨率,将长轴设置为2个亮点距离的2倍,并使短轴等于2点距离。这样的设计一方面可以降低散斑噪声在相对相位求解中的影响,另一方面,可以尽量避免干涉图案中的调制信息被滤除。图3所示为各向同性和各向异性滤波方式下的处理结果,由对比可知图3(c)降低了沿条纹方向图像的噪声,同时保留了条纹的形变。
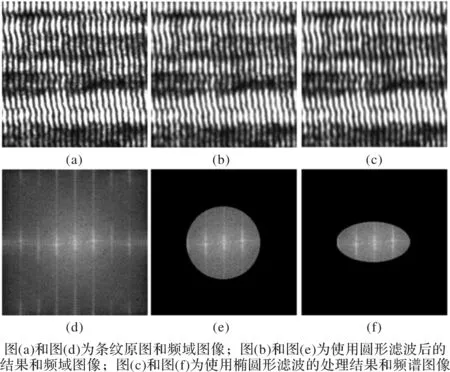
图3 图像预处理方法对比Fig.3 Comparison of different preprocessing methods
2.2 相位调制图提取
相位调制图案的提取由相移法得到。我们使用四步相移法,通过采集4帧等相移的条纹图像来计算包含有被测物体表面三维信息的相位初值,之后通过解包裹,将图像的灰度值与对应像素点的相位调制建立起联系[20]。
假设条纹图像光强是标准正弦分布,则其光强分布函数如(2)式所示。
Ii(x,y)=I′(x,y)+I″(x,y)cos[φ(x,y)+δi]
(2)
式中:I′(x,y)为图像的平均灰度;I″(x,y)为调制幅度;δi分别为图像的相位移;φ(x,y)为待计算的相位主值。
根据(3)式可计算出光栅图像各像素的相位主值。
(3)
通过相移算法计算出的相位主值在一个条纹周期内是唯一的,通过解包裹可以得到连续的绝对相位值φm(x,y).对干涉图像中的条纹周期进行统计计算,得到未经被测样品表面调制的条纹分布,将干涉图案上各像素的绝对相位值与参考平面的绝对相位值相减,可得到被测样品表面相对载物台平面的相位调制图。图4为相位调制图的计算过程示意图。

图4 相位调制图的计算过程Fig.4 Computational process of modulated phase
2.3 噪声点滤除
最后,相位调制图中的噪声需要去除。在相位解包裹过程中,条纹形变可以测量的轴向范围对应的相位差为π,超出该测量范围会产生相位模糊现象,导致相对相位求解错误,产生2π的相位误差,并在计算绝对相位时对后续像素产生影响。在实际测量中,被测样品在个别位置可能存在轴向超出测量范围的情况,可通过计算解包裹方向上相邻像素的相对相位差值来判断各像素处是否存在相位模糊现象,并对该位置处点云进行滤除。此后,可通过计算相位模糊处的后续像素点与垂直于解包裹方向上像素的相对相位差值,消除2π的相位偏差,复原后续像素的真实绝对相位。滤除噪声点前后的绝对相位图如图5所示。
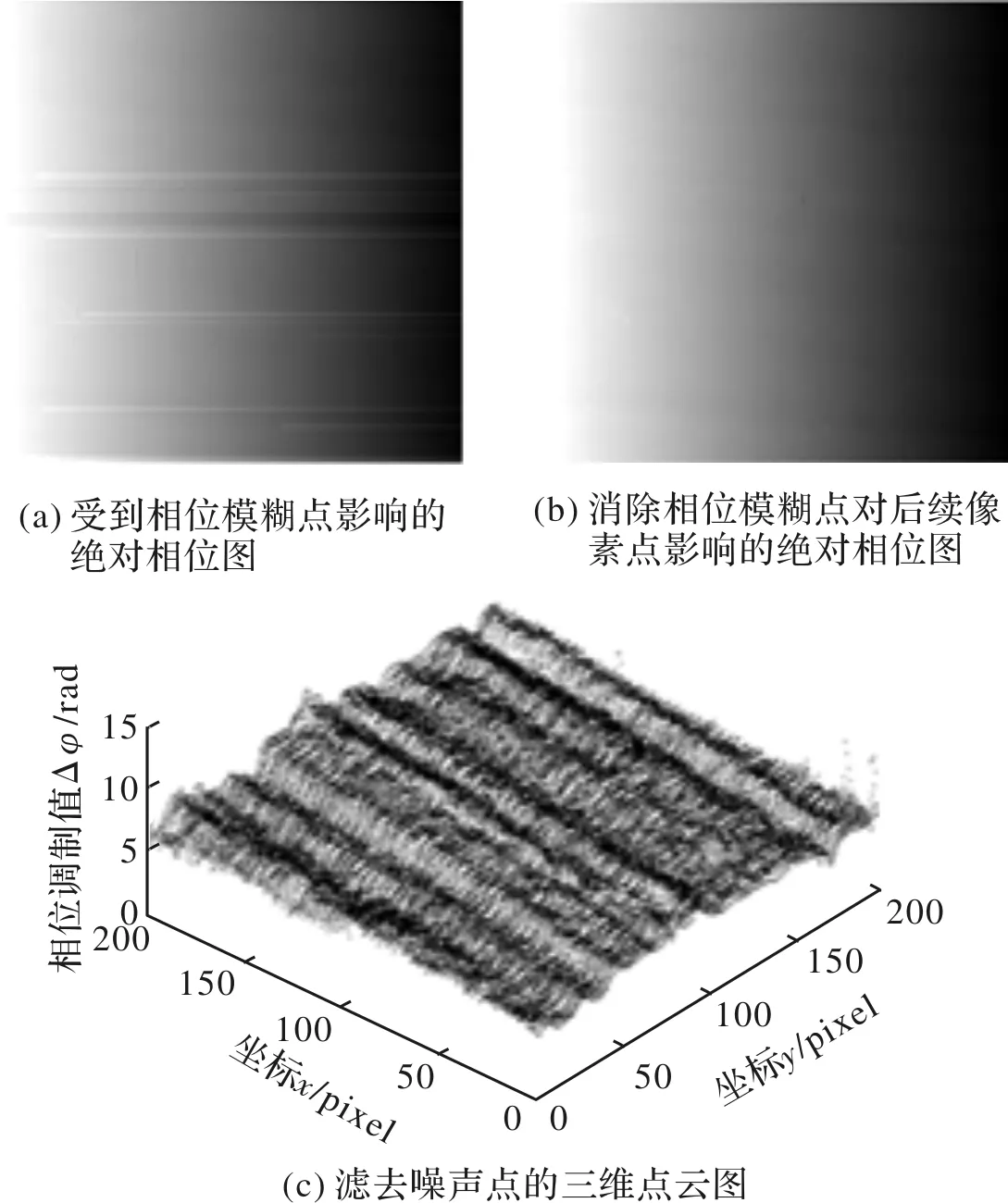
图5 噪声点滤除示意图Fig.5 Removal of noise points
3 数学模型及标定方法
得到样本的相位图后,需要建立数学模型来确定相位变化信息与样本高度关系。对成像和照明光路进行简化后,系统可由图6中的数学模型来表示。图6中,需要注意投影法和干涉法产生条纹的区别,当从外部投影产生条纹时,投影图案的大小会随着被测物面与投影器件的距离而产生较大变化,若投影面不平行于被测物面,条纹的周期不随图像坐标线性变化;而干涉法使用光束干涉产生条纹,并通过物镜进行照明,条纹的产生与杨氏双缝干涉模型类似,因为样本表面的起伏远小于光源距离被测物面的距离,在成像范围内,条纹的周期可认为是近似不变的,所以条纹周期与坐标为线性关系。
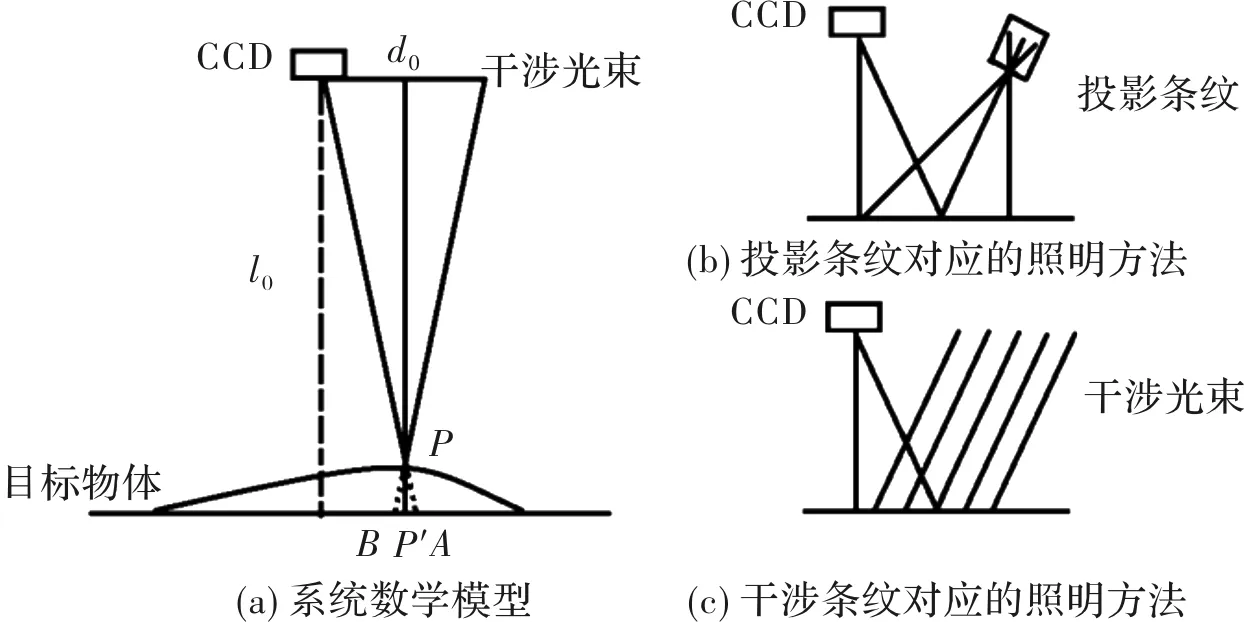
图6 光路数学模型Fig.6 Mathematical model of optic path
图中,P是目标物体上一点,PP′为P点与载物平面的距离,d0为相机与干涉光束之间的距离,l0为相机到物体所在平面的距离,载物平面上照明条纹的周期为T。由于目标物体的调制作用,本应照明到B点的光束被调制到了P点,在相机中显示为条纹由B点调制到了A点。由三角形相似原理可得到(4)式。
(4)
式中:A、B两点距离与相位变化值之间的关系可由(5)式表示。
(5)
由(4)式和(5)式可得相位变化值与高度的关系,如(6)式所示。
(6)
在实际应用中,样本高度PP′远小于相机与载物平面的距离l0,故(6)式可简化为(7)式.
(7)
由(7)式可知样本高度与相位变化值之间呈线性关系。条纹周期T可通过图像进行计算。因此,使用已知高度的样本进行标定,即可求得比例系数。
4 实验结果及重建精度分析
在上述实验设备和重建算法的基础上,本文对Ra=100 nm的粗糙度对比模块进行了三维重建,并使用高度为100 nm的光刻线条进行标定。重建范围为(6.45×6.45)μm2,三维重建结果如图7所示。
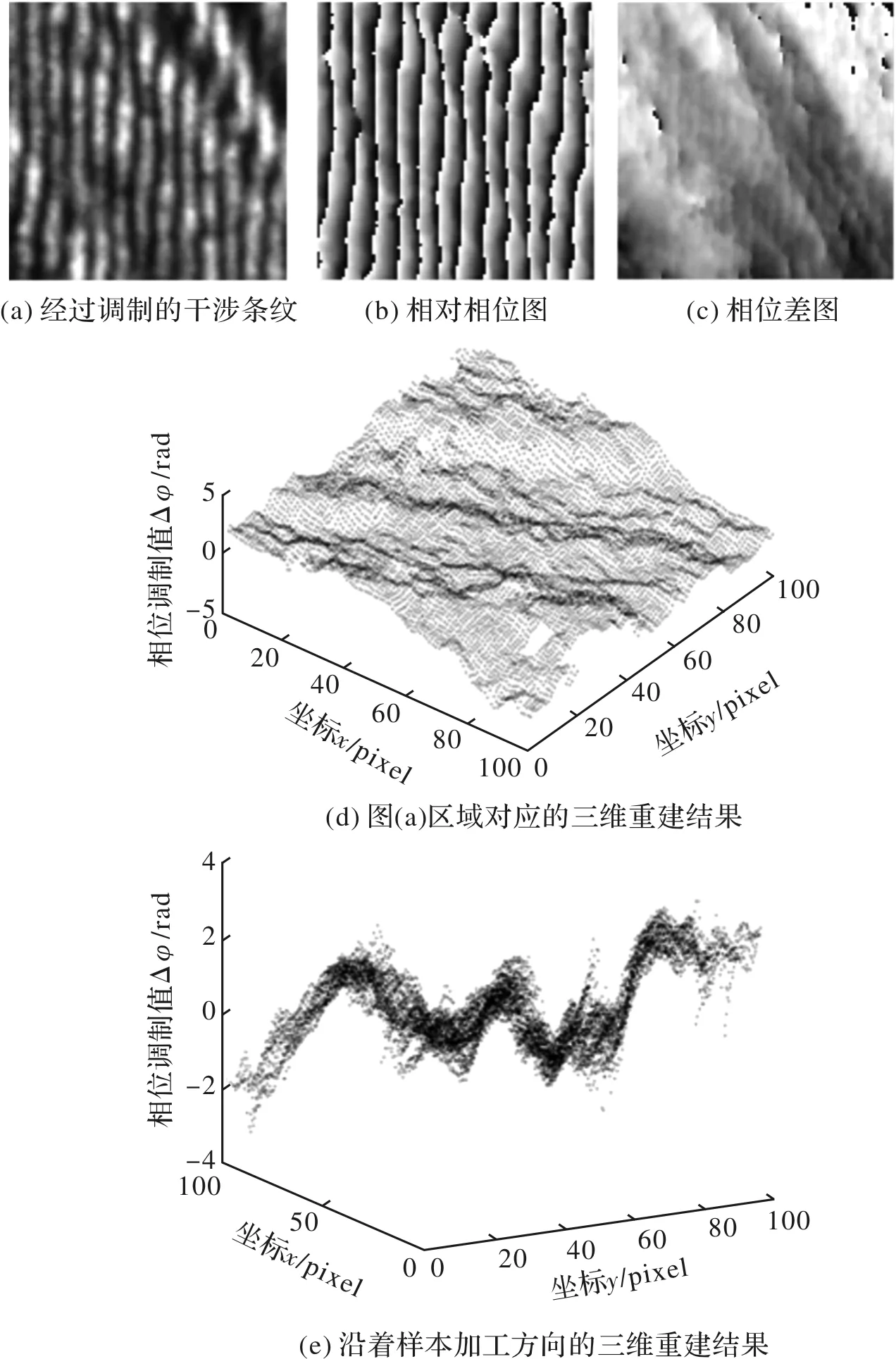
图7 三维重建结果Fig.7 Three dimensional reconstruction result
为对重建精确度进行评估,本文使用干涉条纹对硅片进行照明,并提取6.45 μm范围内各点的相位值进行分析。由图8可知,该范围内各点相位的最大偏差值为0.31,对应高度为14.2 nm,即系统的单次测量误差小于14.2 nm。
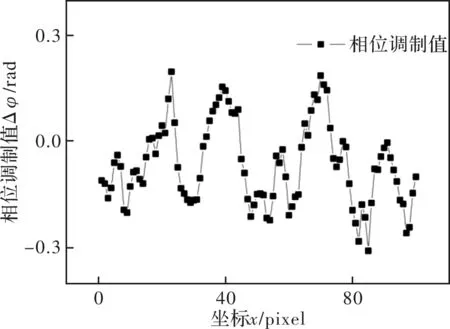
图8 硅片表面干涉条纹相位分布Fig.8 Phase distribution of interference fringe on siliconwafer surface
此外,本文选择高度为100 nm的光刻线条对系统进行标定,对50 nm高的光刻线条进行三维检测。图9为重建后垂直于光刻线条方向上的三维点云分布,使用标定结果,计算得到待测光刻线条的高度为54.1 nm,与真实高度偏差为4.1 nm。
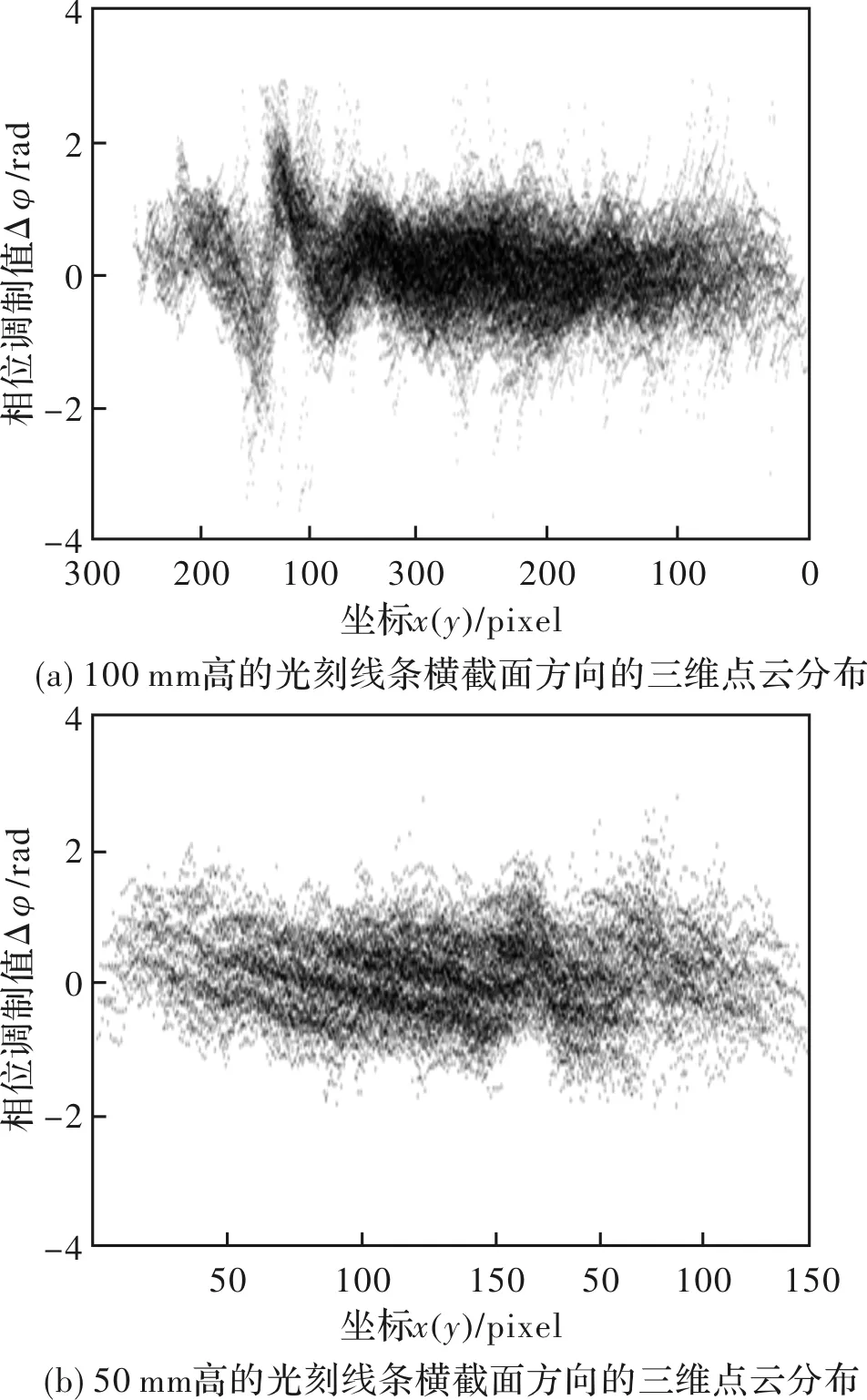
图9 光刻线条的重建结果Fig.9 Reconstruction results of lithography lines
为计算重建的重复性精度,本文选取一个(10.3×10.3)μm2区域进行了5次重建实验,各次重建图像中第1列的相位值分布如图10所示。
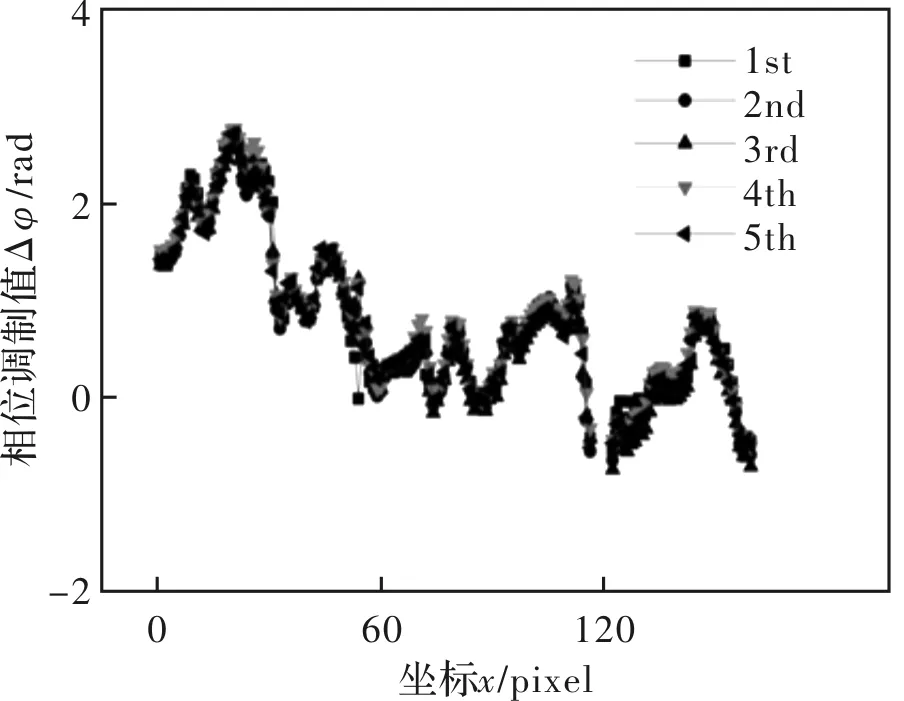
图10 多次测量相位值分布Fig.10 Phase distribution of multiple measurements
由于条纹方向不严格平行于图像边界,相位值随像素点呈递减趋势,但该现象不影响重复性误差的计算。按照贝塞尔公式可计算得到各点标准偏差的估计值,并计算其平均值为0.09,对应高度为4.3 nm,即系统的重复性误差可达8.6 nm(2σ)。
5 结论
本文提出了一种使用非平行光干涉照明的显微镜对微观物体表面进行三维重建的方法。该方法不需借助干涉物镜产生条纹,不需要轴向扫描装置记录条纹变化,可精确调节条纹相位,且所产生的干涉条纹的相位随坐标线性变化。此外,因为照明条纹参数调节光路独立于显微成像光路,系统装置具有光路简洁、易于调节的优点。
