基于仿真优化的MRO调度问题研究

□ 丁金想，栾世超，石晓磊，连福诗

(中国航空综合技术研究所，北京 100028)

1 引言

在航空产业链中，全球民用航空运输市场的发展带动了民用航空维修业(MRO)和民用航空制造业的发展，民用航空维修业的经济价值越来越受到关注和青睐。从行业类型来看，MRO企业属于服务行业，民航公司是其最大客户群，与民航运输业呈相互依存关系[1]。

对于MRO企业来说，除定期维修外，更多的维修工作存在不确定性，例如，飞机故障发生时间、原因、程度不可预测，导致维修的工作内容、时间和周期等无法按例行工作安排，因而MRO企业面临诸多不确定因素，调查显示，47%的MRO公司维修过程中面临着40%-59%不确定工作内容[2]。虽然近年来国内外航空维修市场发展迅速，但是生产管理却面临着很多难以有效解决的问题，如何有效地解决维修生产调度中的问题对于MRO企业提高生产效率、提升生产能力、优化库存管理以及提高客户满意度等方面具有重要意义。

2 国内外研究现状

MRO企业是再制造工业的重要组成部分，一些复杂的特点使得MRO计划与调度问题与传统制造业有很大不同，例如：如拆分-修理-组装的三级结构、待维修件质量水平的不确定、物料匹配需求以及不确定工艺路线和工时。MRO是生产计划与调度的一种新的研究领域，它的复杂性和不确定性引起学术界的广泛关注。

仿真优化是一种适合解决含有不确定性调度问题的有效方法，Guide[3]等人研究了再制造的调度策略，分解机制和优先调度规则被建立在仿真模型中，通过大量的对比实验证明了最早交期(EDD)的调度规则往往能够得到很不错的结果，而分解机制的不同对调度效果的影响比较小。Guide等人[4]以最短交货期为目标，研究了调度规则对再制造系统的订单执行策略的影响，结果表明，通过采用简单的调度规则能显著提高再制造系统的性能指标。Christoph[5]等人将研究目标定位于寻找适合修理车间job-shop运作的调度规则，首先假设使用调度规则可以提高调度结果，考虑到MRO系统的复杂特点，文章通过建立仿真模型，将准时交货率、在制品率、利用率以及生产周期作为衡量标准，结果表明，调度规则对MRO的调度效果的确有一定的影响，并且发现FIFO/Slack和ESD/Slack的规则组合会取得更好的效果。

Kim[6]等人首先分析了再制造系统的复杂特点，考虑到分解-修理-组装的三级结构，并将决策变量定义为待维修件在分解车间中被分解的顺序、子部件在修理车间中每个工作站前的修理顺序以及待维修件在组装车间被组装的顺序，文章建立基于仿真的整数规划模型，通过分析，认为该模型是NP-hard问题，文章提出基于调度规则的启发式算法、基于NEH的启发式算法以及IG(Iterated greedy)算法进行求解，并通过大量算例对比分析了不同启发式算法的优缺点。然而，模型中针对修理车间的建模是确定的，他们认为子部件在修理车间有固定的维修工艺路线，此外也没有考虑到工时的不确定性。

郝[1]等人在对航空维修企业调度问题国内外研究现状详细分析的基础上，建立以最小化期望权重延误时间为目标的混合整数线性规划模型，因为该问题是NP-hard问题，通过使用传统的优化方法很难求得最优解，他们提出基于多精度仿真模型的MO2TOS算法对该问题求解，并通过基于实际背景的算例验证了模型的可行性。然而，当问题规模增大时，由于解空间巨大，MO2TOS算法将不再适合求解该问题。本文的研究背景是在该研究基础上开展的，通过基于仿真优化的方法解决大规模问题情况下的MRO调度问题。

3 MRO调度问题建模

3.1 MRO问题描述

一般的MRO系统基本框架包含三个车间，为了简便，即使现实中每个车间可能包含多个，但我们考虑每种车间只含有一个，三个车间各自主要的工序内容如下：

分解车间：分解维修件、清洗以及检测；

修理车间：包含很多不同的工序和机器，一般认为是job-shop类型，子部件在该车间的工艺流程不确定；

组装车间：组装和最后的检验。

待维修件首先在分解车间根据BOM结构分解形成若干子部件，每个子部件的检测后状态可能是修理、完好、报废三种状态中的一种，每种维修状态表示子部件在修理车间不同的维修工艺路线，因此，每个子部件的实际工艺路线是不知道的，直到待维修件完成分解和检测工序；此外，因为子部件损坏程度不同，即使对于两个相同的子部件，其在同一个工序上的加工时间也存在不确定性。

可见，整个维修过程受到很多约束条件，在我们的问题中，对于N个给定的待维修件，决策变量是待维修件在分解车间分解的先后顺序、拆分出的子部件在修理车间每个工序上的修理顺序、以及子部件在组装车间的组装顺序。优化目标是期望权重延误时间之和最小。

3.2 MRO调度问题的仿真模型

如上文所述，MRO问题不确定性因素多(不确定达到时间，不确定加工时间，不确定工艺路线等)，问题结构复杂，为了实现对该问题的求解，结合作者在一家航空维修企业的项目经历，为不失一般性，本文对所研究的这类MRO调度问题做出以下假设：

整个MRO系统只由一个分解车间、一个修理车间和一个组装车间构成；

分解车间和组装车间分别由一个工序组成，每种工序只包含一个机器；

修理车间有多种工序类型，每个子部件在修理车间的工艺路线是不确定的；

修理车间每个工序只包含一个机器；

每个拆分出的子部件都只能组装到原主部件上；

每个机器同一时间只能加工一个部件。

首先我们基于C++建立以最小化期望权重延误时间为目标的仿真模型，示意图如图1所示。

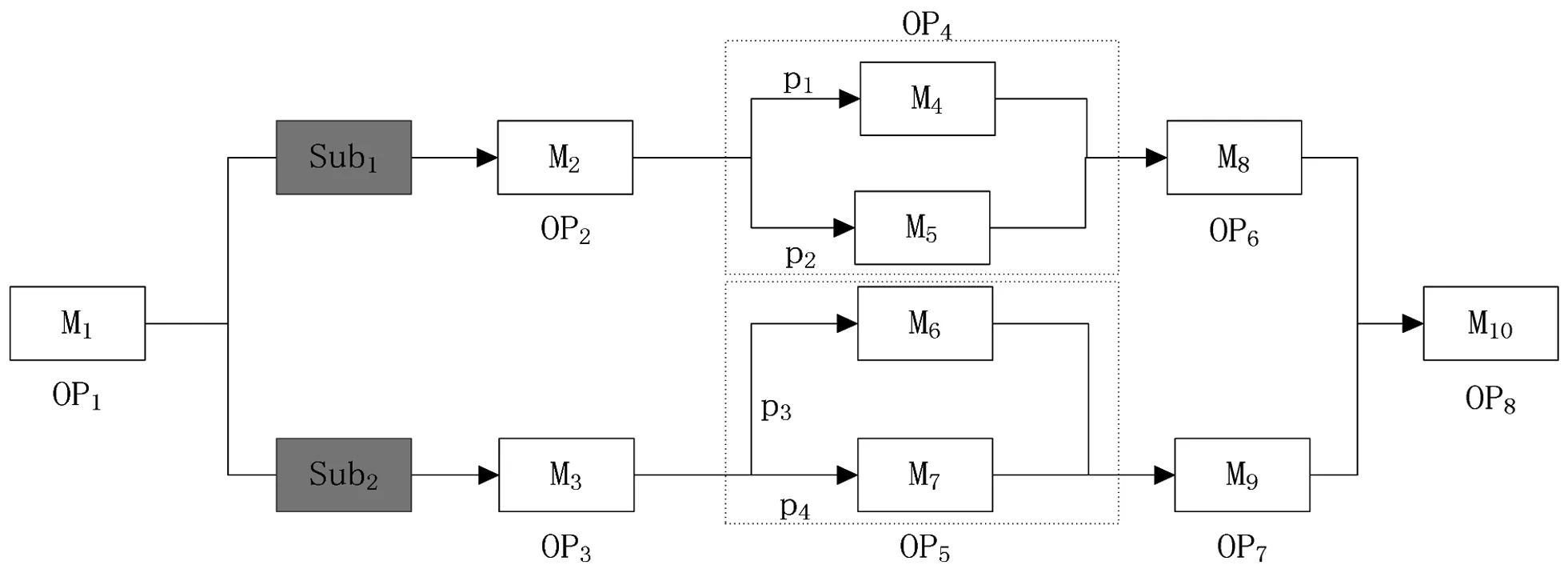
图1 MRO系统结构图

其中OP1和OP8分别表示分解车间和组装车间，剩余工序表示修理车间。假设调度开始时刻，n个待维修件已经可以被安排调度，所有待维修件在每个机器上的加工顺序是相同的，这个顺序也是我们要决策的，其中OP4和OP5各自拥有两个不同的机器处理不同的工作内容，并且各自拥有一个概率值，这体现出MRO系统在修理车间的工艺路线不确定性。基于实际的维修企业信息，并不是所有的工序的加工时间都是不确定的，例如，清洗工序。因此，我们只假设OP6和OP7有不确定的加工时间，其他工序加工时间是确定的。

4 基于仿真优化的MRO调度问题算法研究

4.1 调度规则

调度规则算法是一种简单、易操作的启发式算法，因为其具有容易理解和方便实现的特点，在实际中有着广泛的应用。在我们问题中，所有待维修件或子部件在分解车间、修理车间和组装车间内所有工序上的加工顺序需要决策。每个工序前都可以通过指定一种规则来实现调度，根据现有文献中对调度规则的研究[6]，我们对常见并且有效的调度规则分为两类，如表1所示。其中，第一类调度规则可以考虑到待维修件在其维修工艺路线上所有工序的加工特点，而第二类调度规则主要针对某个特定工序。

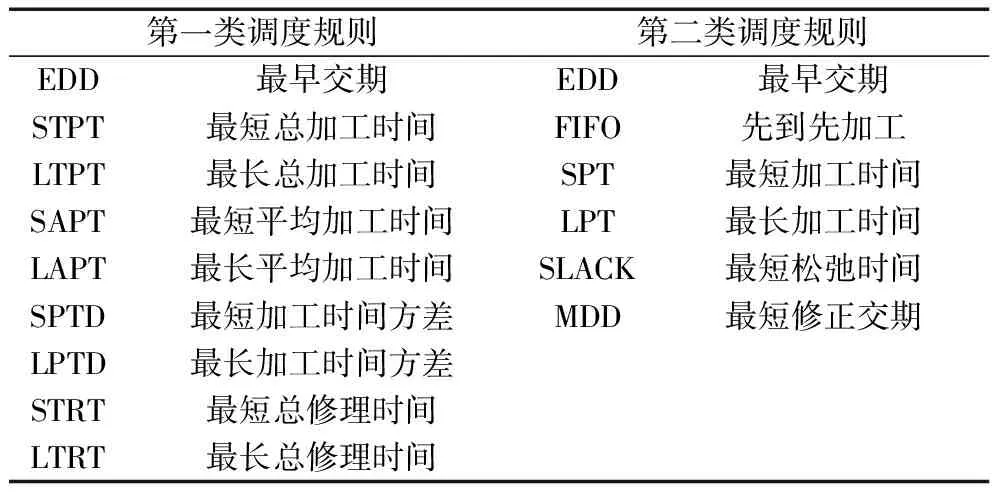
表1 两类调度规则

对于所有待维修件在分解车间中分解工序前的加工顺序，我们采用第一类调度规则；对于子部件在修理车间以及组装车间中工序前的加工顺序，我们采用第二类调度规则。显然为了实现MRO企业维修现场的生产调度，选择何种调度规则组合是我们要研究的问题。

4.2 NEH算法

在构造型启发式算法中，Nawaz-Enscore-Ham(NEH)[7]被认为是计算以make-span为目标的排列flow-shop问题的一种非常高效的算法[6][8]。基于NEH算法的基本思路，Fernandez-Viagas[9]等人提出一种适用于以延误时间为目标的改进NEH算法。这种新的NEH算法与传统NEH算法有两方面不同：第一，以EDD规则得到的解作为NEH的初始解；第二，通过计算总延误时间来评价一个部分顺序。

针对MRO仿真模型，我们通过NEH求解待维修件在分解车间的加工顺序，对于修理车间和组装车间内工序前的加工顺序，我们通过调度规则得到加工顺序。与一般NEH算法相比，本文提出的NEH算法会考虑不同调度规则得到的解作为NEH初始解，与修理车间和组装车间的调度规则的最佳组合。此外，在算法执行过程中，对于具有相同目标函数的两个顺序，我们通过使用最小总空闲时间[10]的选择机制进行选择，而非随机选择。

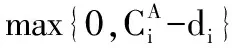
步骤1：通过上节调度规则中给出的某种第一类调度规则得到一个初始顺序，记为Seq0=(J1,J2,…,Jn)；

步骤2：设置k=2，从Seq0中选择前两个待维修件J1和J2，分别形成序列(J1,J2)和(J2,J1)，计算各自的tardiness，以较小tardiness的序列作为当前序列Seq，假设Seq=J1,J2,…,Jn；

步骤3：设置k=3，如果k≤N，转向步骤4；否则转向步骤7；

步骤4：从Seq0中选择第k个待维修件；

步骤5：将待维修件Jk分别插入到序列Seq中的k个可能位置，得到k个新的序列，如：{Jk,J1,J2,…,Jk-1}，{J1,Jk,J2,…,Jk-1},…,{J1,J2,…,Jk-1),Jk}。计算各自的tardiness，把最小tardiness的序列作为当前序列Seq；如果有多个相同的最小tardiness，则通过最小总空闲时间的选择机制进行选择。

步骤6：设置k=k+1，转向步骤3。

步骤7：把当前序列Seq作为NEH算法得到的最优调度顺序，并输出该顺序，算法结束。

4.3 遗传算法(GA)

NEH算法虽然效率高，但只是一个局部搜索的构造型启发式算法，为了获得更好的解，我们需要具有全局搜索特性的改进型启发式算法。在生产计划与调度领域，遗传算法(GA)已经被广泛应用于求解NP-hard组合优化问题[10][11][12]。基于生物进化的“优胜劣汰”原理，GA通过选择、交叉和变异操作来实现群体并行优化。作为一种通用的全局优化算法，GA近年来在各领域得到广泛应用，但大量研究表明GA存在易早熟、算法参数敏感等缺点，取得良好的性能需要依赖较大的种群并对算法参数作精心设计[13]。

在遗传算法中，我们直接通过顺序编号作为染色体编码。针对本文提出的问题，与NEH算法一样，通过GA求解待维修件在分解车间的加工顺序，对于修理车间和组装车间内工序前的加工顺序，我们通过调度规则得到加工顺序。

染色体的表示：因为本文模型是求解分解车间待维修件的加工顺序，因此可以直接用自然数顺序编码。假设当前有8个待维修件，编号分别为1,2,3,4,5,6,7,8。则某一排列(染色体)可为：86 2 3 7 5 1 4。

交叉操作方法：本文采用典型的PMX方法，假如有两个个体A和B，A：8 62 3 75 1 4，B：1 5 4 2 8 6 3 7。PMX 操作方法的基本过程如下：首先在A、B 染色体上随机选取一段，例如2,3,7 和4,2,8，用该段内的基因对应关系来决定一系列的交换，杂交变换后的新个体A和B分别为：7 64 2 85 1 3，1 5 2 3 7 6 4 8。

该算法的具体步骤如下：

步骤1：设置参数，根据文献对GA参数的研究，我们设置种群大小为2.5*n，迭代次数为3*n，交叉和变异概率分别为0.75和0.25。

步骤2：设置t=0；通过随机产生的方式初始化种群S(0)；

步骤3：通过计算适应度函数来评价种群S(0)中所有个体；

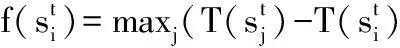
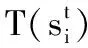
步骤4：计算选择概率；

步骤5：如果t>3*n，转向步骤11；否则，转向步骤6；

步骤6：设置t=t+1；

步骤7：从种群S(t-1)选择新的种群S(t)；

步骤8：交叉操作，交叉操作使用PMX方法[10][14]；

步骤9：变异；

步骤10：评价新的种群S(t)；

步骤11：把当前种群中适应度值最高的顺序作为GA算法得到的调度顺序，输出该顺序，算法结束。

上面给出的GA算法的初始种群完全是随机产生的，本文对这种传统的GA算法进行改进，改进的GA算法的初始种群中有一个个体是NEH算法的解，并且有0.25*n个个体是以NEH的解为基础随机变异产生的，在GA迭代过程中，始终保证每代种群中最优秀的个体被保留下来。

4.4 算例设计与结果分析

为了研究不同算法在处理MRO调度问题上的效果，本节我们设计一系列算例进行验证，并对计算结果进行对比分析。这设计算例时，我们需要考虑以下四个变量：待维修件数量、每个待维修件可以拆分的子部件数量、每个子部件可能的工艺路线个数以及每个子部件所有可能工艺路线上的最大工序个数。

本文给出的算例中，待维修件数量可以为(6,10,15,30,50)，每个待维修件可以拆分出的子部件个数为(2,3)，对于每一个子部件，其可能的工艺路线为(2,3)，而对于每个子部件，其所有工艺路线中最大工序个数为(3,5,7)。根据这些参数，我们可以随机产生60个算例，为了表述方便，对其进行编号如表2所示：

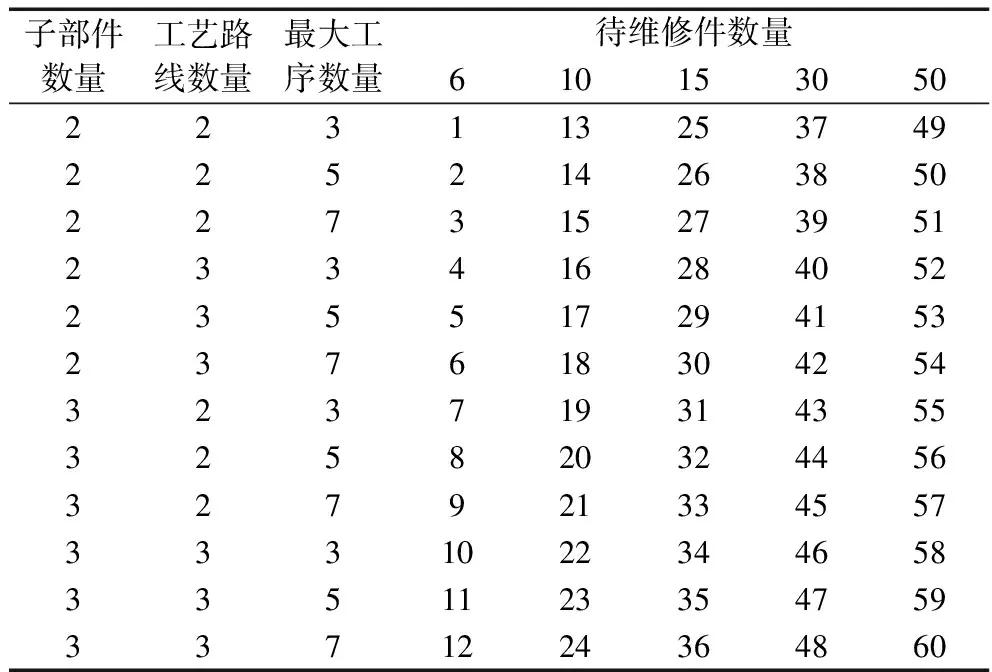
表2 60个算例编号

在随机产生算例时，考虑到模型中工时和工艺路线是不确定的，所以，我们将每个工序的工时设定为一个三点分布，例(2,4,5)，而这三个值相应的概率从U(0,1)中随机产生，例(0.1,0.6,0.3)。其中U(a,b)表示一个在区间[a,b]内的均匀分布。具体来讲，基于一定的实际数据，每个待维修件在修理车间任一工序的工时从U(2,6)中产生，而在分解车间和组装车间任一工序的工时从U(1,3)中产生。

每个待维修件的交期(due date)从U(P(1-T-R/2),P(1-T+R/2))中随机产生[15]，其中T和R分别表示延迟参数和交期范围参数，并分别设置为0.37和0.26，P是make-span的下界，每个待维修件的延迟权重(λ值)从U(1,2)中随机产生。

本文所有算法程序都使用C++编码，并在英特尔酷睿i3，主频3.40GHz的CPU和4.00GB内存的64位win7电脑上进行运算。对于每个解，我们设置仿真次数为1000以消除噪音获得稳定目标函数值。

由于篇幅有限，不失一般性，我们只展示编号为(6,12,18,24,30,36,42,48,54,60)的算例的计算结果。为了比较不同算法的表现，两种测量标准在本文被采用，分别是平均相对性能比率(ARPR)和平均提高百分比(API)。

其中，Heuristici表示对于第i个算例，该启发式算法计算得到的目标函数值，Besti表示对于第i个算例，所有启发式算法得到的最好值。为了比较不同算法的计算效果，我们计算每个目标函数值的均值和方差，最优性比较是基于假设检验，下文所有结果的置信度都是95%。

调度规则：表1给出了调度规则算法的表现，因为第一类调度规则有9种，第二类调度规则有6中，所以一共具有54种组合。因篇幅限制，本文根据平均ARPR值的大小只给出最好3种和最差3种的组合。其中EDD-FIFO表示分解车间的调度规则是EDD，而修理和组装车间的调度规则是FIFO。

从表3可以看出，EDD-EDD、EDD-FIFO和STPT-FIFO三种调度规则普遍来说表现比较好，但是并不能说其中哪一种调度规则绝对比其他更好。随着问题规模增大，显然EDD-EDD调度规则逐渐更具有优势。此外，调度规则算法计算速度很快，即使对于包含50个待维修件的算例-60，其计算时间也在1秒之内，这也是调度规则能够在实际中广泛使用的原因之一。

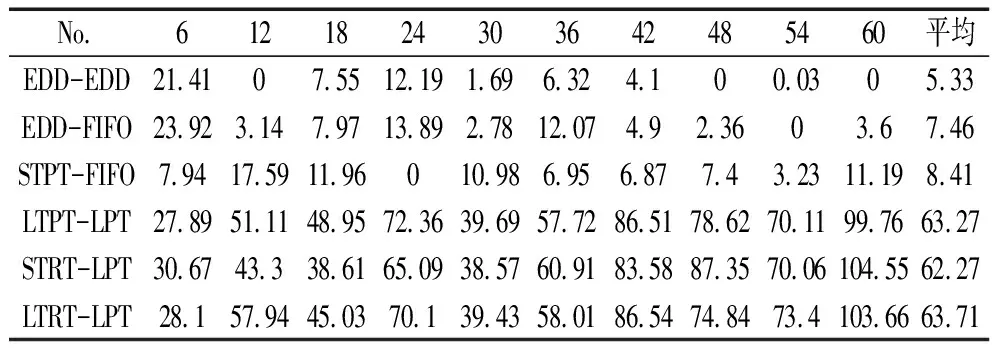
表3 ARPR结果对于调度规则算法

NEH算法：NEH算法的计算时间要比调度规则大，对于算例60，NEH算法的计算时间约为8分钟。虽然NEH算法的计算比较耗时，但是其解的质量相对于调度规则也有一定的提高，表4给出NEH算法与同种调度规则相比解的API值。从表4可以看出，当把调度规则作为NEH的初始解时，NEH算法获得的解的质量有很大的提高，最大的提高值可以达到23.51%(如NEH-LTRT-FIFO)。显然，从解的质量方面来看，即使调度规则支持快速决策，但是解的质量仍有很大的提升空间。

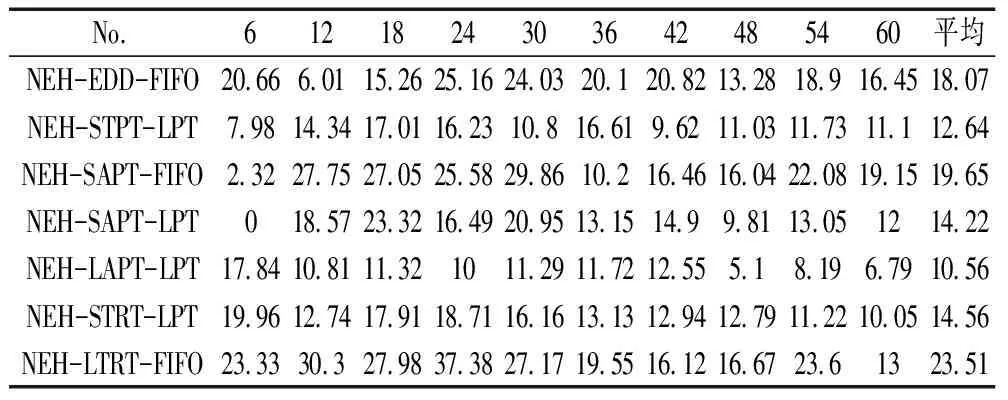
表4 NEH算法与调度规则相比的API值

GA算法：表5给出了GA算法、NEH算法的比较评价，表中的值都是与同种组合的调度规则相比得到的API。根据表3、4的结果，我们可以看出不管是NEH算法还是调度规则，EDD-FIFO和STPT-FIFO两种组合表现的都比较好。所以在验证GA算法表现时，我们只展示这两种组合分别作为GA的初始解时GA解的情况。在表5中，符号GA-EDD-FIFO中，EDD-FIFO表示将NEH-EDD-FIFO算法得到的解作为GA算法初始种群中的一个，与其它算法一样，FIFO表示修理车间和组装车间的调度规则是FIFO。

从表5中可以看出，对于给出的算例，GA-EDD-FIFO和GA-STPT-FIFO两种组合得到的解与相同组合的调度规则得到的解相比，其平均API值分别为21.16%和21.18%，而对于NEH-EDD-FIFO和NEH-STPT-FIFO两种组合，其平均API值分别为18.07%和16.57%。所以，与NEH算法相比，有初始解的GA算法可以得到质量更高的解。相比有初始解的GA算法，纯GA算法的平均API仍然大于NEH算法，但是随着待维修件数量增大，纯GA算法的API值远小于有初始解的GA算法，可见，纯GA算法此时效率较低，改进的GA算法表现优于纯GA算法。

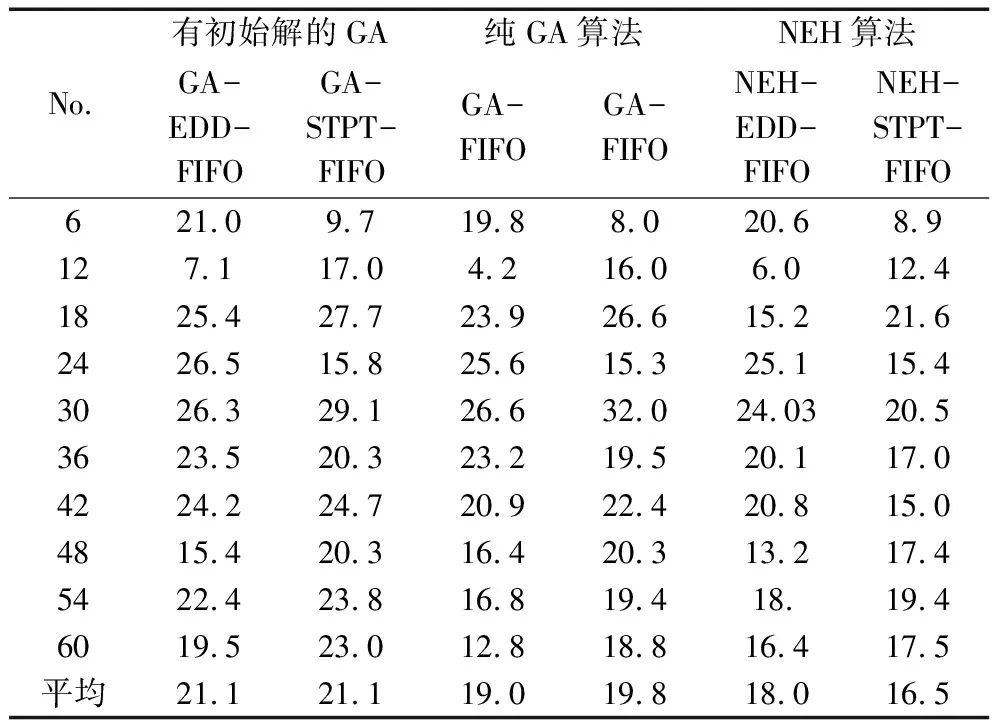
表5 GA、NEH算法分别与调度规则相比的API值

同样我们可以注意到，对于同种调度规则组合，NEH算法对解质量的提高百分比大于GA算法对NEH算法解质量的提高百分比，这可能是因为GA算法得到的解已经接近最优解或者是GA算法并没有比NEH算法好太多。然而从算法计算时间方面来看，GA算法是非常耗时的，表5中GA算法最大计算时间设为3600秒。因此，实际应用中，当对解的质量要求很高时，GA算法才有应用价值。

5 结论

本文针对MRO调度问题的复杂性和不确定性构建仿真模型，并提出三种启发式算法，分别是调度规则、NEH算法和GA算法，其中NEH算法属于构造型启发式算法，GA属于改进型启发式算法。然后对三种启发式算法的计算流程进行详细介绍，本文最后给出若干计算算例，分别使用三种启发式算法进行计算，并将计算结果进行展示和对比分析。

通过大量算例可以得出结论：调度规则算法计算时间快，但计算结果较差，GA算法的计算结果最好，但是非常耗时，适用于对解的质量要求很高的情况下，而NEH算法在计算时间和求解质量方面居于调度规则和GA之间。