方舱轴流风机机罩降噪研究
2019-05-23陆嘉伟陈言东王伟利王良模
陆嘉伟,王 陶,陈言东,王伟利,黄 健,王良模
(1.南京理工大学 机械工程学院, 南京 210094; 2.苏州江南航天机电工业有限公司, 江苏 苏州 215300)
对于方舱这类用于工作、居住的特种车辆而言,舱内的噪声水平极大地影响了内部人员的工作效率和居住心情。因此,本文以某方舱用于通风的轴流风机为研究对象,研究风机的降噪技术以提高方舱内部舒适性。
随着当前计算流体力学(CFD)和计算气动声学(CAA)技术的发展,轴流风机的气动噪声研究成为热点。目前大部分研究都从风机本体的降噪入手,风机叶片旋转与空气的相互作用是主要噪声源,因此研究多针对叶片的结构进行调整。赵立杰等[1]和周翔[2]研究发现,减小风机叶尖间隙不仅可以提高风机的性能,还可以达到降噪的效果。周翔[2]和Nashimoto[3]等在风机叶片上安装分流翼片,用于改善叶片表面的气流分布情况,有效降低了噪声。周翔[2]和周雪[4]在文中指出,在叶片合适的位置进行穿孔,控制孔径的大小也能降噪。左曙光等[5]发现改变叶片厚度,气动噪声几乎没有变化,可从该角度对叶片进行轻量化设计。
但是,目前研究多集中在风机叶片的尺寸结构设计及其对风机气动噪声特性的影响,对于风机机罩降噪设计的研究较少。现实中许多应用场合出于安全、美观或其他考虑,会安装风机罩,而风机罩结构的不合理设计也会产生噪声,因此对风机罩的优化设计问题进行研究同样具有重要意义。张亚东等[6]对风机端盖的栅格倾斜角度进行研究发现,出风口的结构严重影响了气流流出,是产生气动噪声的重要因素。Yoshida等[7]也指出发动机风机罩在布置空间有限的情况下通常是不规则形状,这对于气动噪声影响极大,需对其进行合理的结构优化来降低噪声。
常用的3种气动噪声模型分别是直接模拟模型、宽频噪声模型和FW-H噪声模型。直接模拟模型计算量巨大,在工程计算中一般不作考虑。宽频噪声建立在稳态运算的基础上,耗费的计算资源少,可以快速定位噪声源。该方法更适合于前期的结构优化,在工程问题中的实用性很强[1]。张亚东[6]和王宽[8]等运用宽频噪声模型分别计算了发动机和风机的气动噪声分布情况,为优化提供了参考。FW-H噪声模型一般用于计算远场噪声,建立在瞬态分析的基础上,针对气动噪声这类高度非定常问题,其结果较为准确可靠。范士杰等[9]运用了FW-H模型对风机作瞬态分析来预测接收者位置的噪声大小。
本文首先运用大涡模拟(LES)方法进行非定常分析,通过FW-H模型分析风机的远场监测点处的气动噪声特性。将结果与加入风机罩后的气动噪声进行对比分析。进一步运用宽频噪声模型研究不同风机罩安装距离下风机罩表面偶极子噪声的变化规律。最后,基于数值模拟的结果,提出风机罩改进方案,通过仿真分析验证优化效果。
1 数值模拟方法
气动噪声的计算分为2个过程:首先是流场分析,采用Standardk-ε湍流模型进行稳态计算得到流场分布[10],并以稳态流场结果作为初始值,继续采用LES模型进行瞬态分析[11],通过监测点处的变量变化判断收敛情况;然后是声场计算,在瞬态分析结果的基础上,激活FW-H模型,设置噪声源和监测点,可以得到远场监测点的声压频谱曲线以及噪声总声压级。在稳态分析结果的基础上,运用宽频噪声模型则可以得到风机和风机罩表面的偶极子噪声分布情况。
1.1 稳态分析方法
稳态计算选择工程计算应用较为广泛的基于RANS模拟的Standardk-ε湍流模型,该模型拥有较好的收敛性。忽略重力的影响,压力速度耦合方式采用SIMPLE。湍流动能和湍流耗散率方程的求解先采用1阶迎风格式加快收敛速度,再用2阶迎风格式提高求解精度。收敛条件设定为残差小于10-3且所观测的变量基本保持稳定。
湍流动能k和湍流耗散率ε的控制方程[12]分别为:
(1)
(2)
式中:ρ为密度;μ为动力黏度系数;μt为湍流黏性系数;Gk为平均速度梯度引起的湍流动能生成项;常数C1ε=1.44,C2ε=1.92,σk=1,σε=1.3。
轴流风机是旋转机械,气流属于非定常运动,旋转域需使用多参考坐标系(MRF)模型[13-14],可将非定常问题转化为定常问题,得到稳态流场的计算结果。
1.2 瞬态分析方法
瞬态计算选用LES模型,亚格子模型为Smagorinsky-Lilly模型,压力速度耦合采用PISO,连续性方程为PRESTO!格式,时间差分格式为2阶隐式。收敛条件同样为残差小于10-3且所观测的变量基本保持稳定。MRF模型只适用于稳态分析,在瞬态分析时,旋转域部分需要将MRF模型切换为滑移网格模型。
除此以外,瞬态分析的时间步长尤为重要,通常步长越小收敛性越好,但是会增加计算时间。此处综合考虑计算时间以及收敛性,经过试算,最终以5×10-5为步长,计算1 500个时间步,直到观测的变量基本保持稳定方可结束计算。
LES方法直接计算流场中尺度较大涡运动的瞬时N-S方程,并用亚格子模型来模拟小尺度涡的影响,其控制方程[12]为:
(3)
(4)
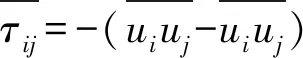
(5)
式中:δij为单位张量;μi为亚格子湍流黏性系数;Sij为求解尺度下的应变张量的分量:
(6)
1.3 气动噪声分析方法
任何实际声源都可以看作由适当相位和幅值的单极子的一个分布系统所组成,可以采用偶极子和四极子这种单极的特殊组合,将之直观反映出来,通常贡献最大的部分是偶极子噪声[15-16],与实际仿真结果相符,因此以下的分析仅考察偶极子噪声。
宽频噪声模型的湍流参数通过RANS方程求解,然后利用半经验修正模型计算噪声功率。其中,求解偶极子噪声和四极子噪声分别采用Turbulent Boundary Layer Noise源项模型和Proudman方程[17],得到噪声源的声功率级。Fluent中用Surface Acoustic Power Level(dB)来评价局部偶极子噪声源对总噪声的贡献。
1969年,Ffowcs Williams和Hawkings将Curle方程推广到考虑运动物体边界影响,得到了目前广泛运用的FW-H方程,其微分形式如下(等式右边3项分别为单极子、偶极子和四极子声源[6,11]):
▽f]-
(7)
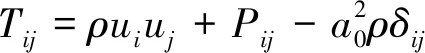
(8)
式中:p′为气体压强;p为静压;ni为法向;vn为法向速度;a0为声速;δ(f)为δ函数;H(f)为Heaviside函数。
2 CFD模型建立
2.1 几何模型
图1为某方舱用于通风的轴流风机模型,带有6片旋转叶片,该风机的最大转速为2 400 r/min。图2为公司原来所采用的风机罩示意图,出口为72个形状大小相同且等间距排列的圆角矩形。
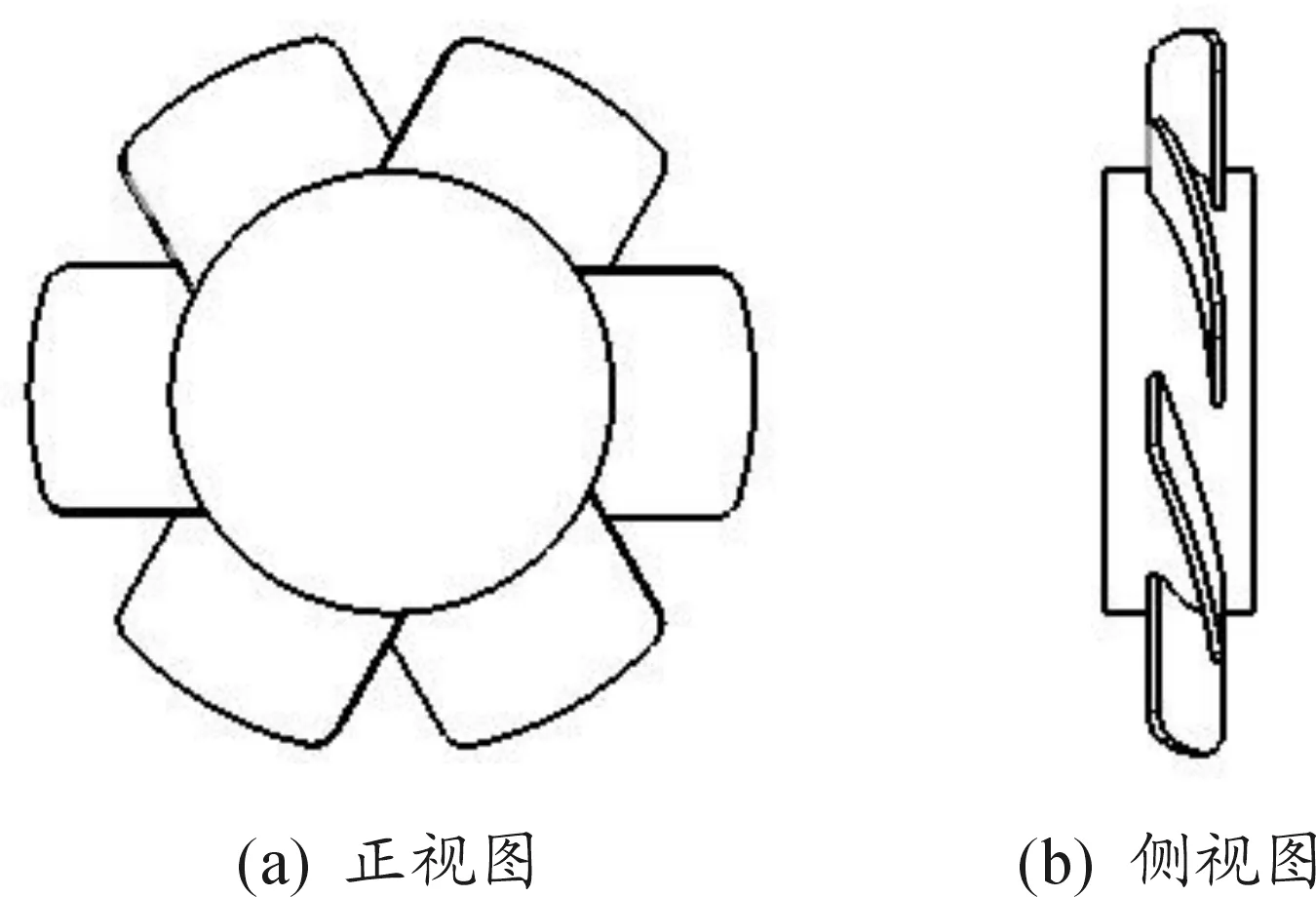
图1 轴流风机三维模型

图2 风机罩示意图
2.2 计算域建立
风机壳的内径为130 mm,风机叶顶间隙为1 mm,因此为保证计算域的合理性[2],此处将旋转域直径设置为129 mm,留0.5 mm与风机壳之间的间隙为静止域,两者交界面设置为“interface”,用于数据传递[1],如图3所示。
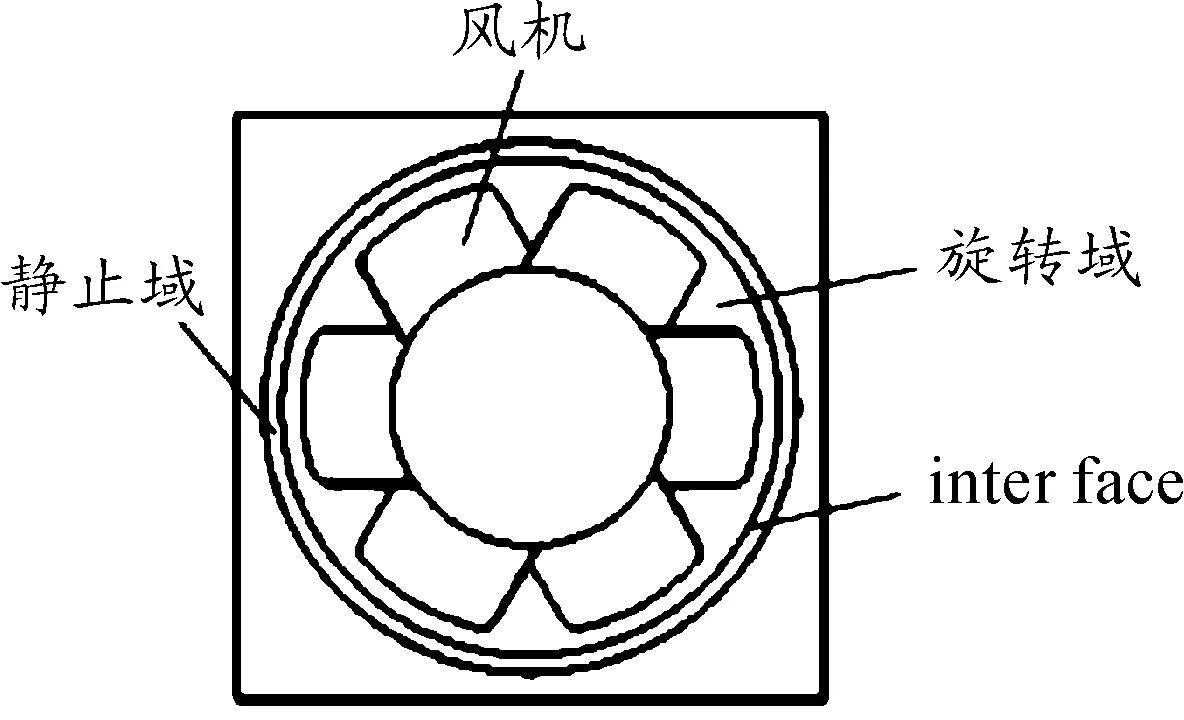
图3 风机旋转域示意图
计算域主要分为4部分,分别是入口扩展段、旋转域、管道段以及出口扩展段,具体的尺寸参数如图4所示。
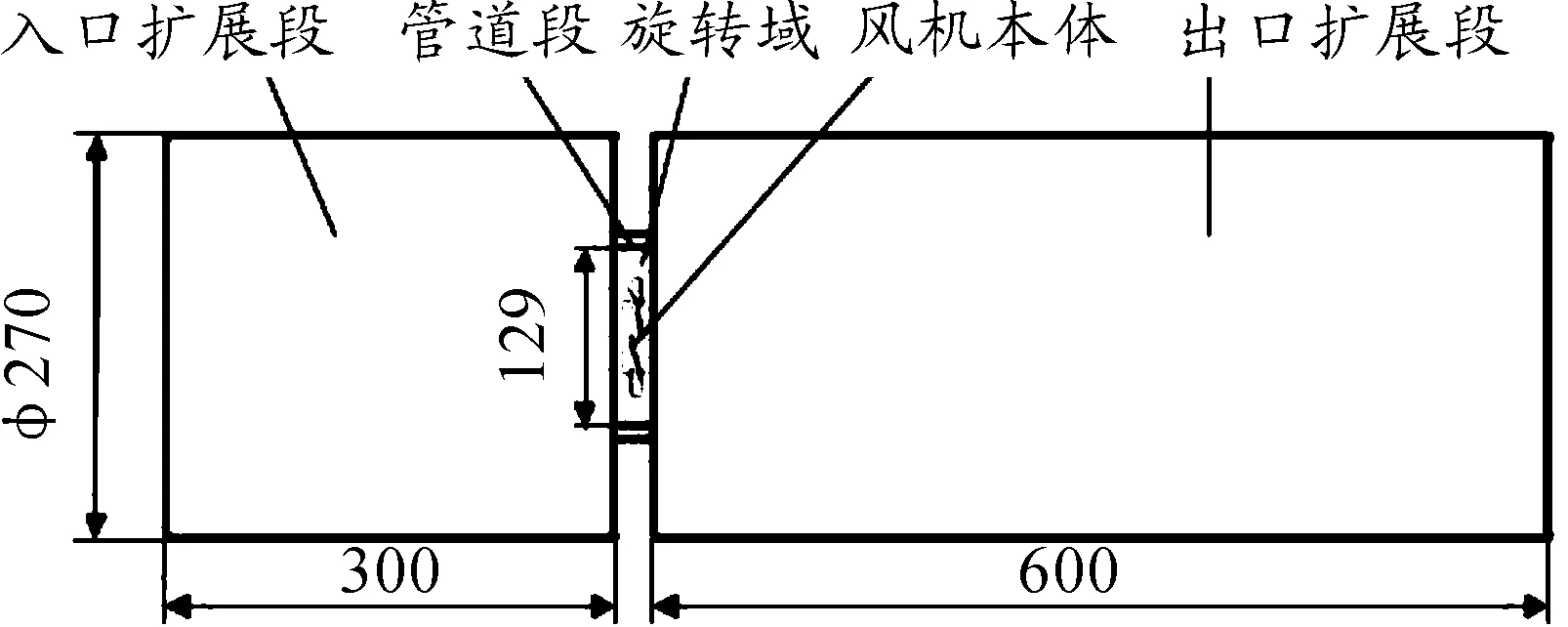
图4 计算域设置
旋转域全部采用与几何贴合更好的四面体网格,对叶片所在区域进行加密处理。为了保证风机核心区域气流流动的稳定性,对入口和出口段的计算域进行适当的延长处理[18]。入口、出口扩展段以及管道段形状较规则,因此采用六面体网格进行划分,后续加入风机罩后,出口扩展段几何变得复杂,改为四面体网格划分。图5为单风机时的计算域网格模型。

图5 计算域网格模型
2.3 网格无关性验证
网格划分时网格质量主要考察对Fluent计算收敛性影响较大的偏斜率和长宽比。为了消除网格划分带来的计算误差,需要对模型进行网格无关性检验[1-2]。在保证网格质量的前提下,选择了4种不同数量的网格,单元数分别为 624 213、1 092 503、1 965 067和 3 491 473。将风机表面的偶极子噪声以及出口面速度作为监测目标,最终得到的3组数据如表1所示。
从表1中数据看出,随着网格的不断加密,计算结果趋于稳定。网格数达到200万以上时,速度值基本变化不大,偶极子噪声变化不超过2%,可以认为计算结果与网格数量之间已无明显关联。对于非结构网格来说,通常网格数量的增加会使计算结果更准确,但也并非越多越好。综合考虑准确性以及计算效率,控制网格数量在200万左右。
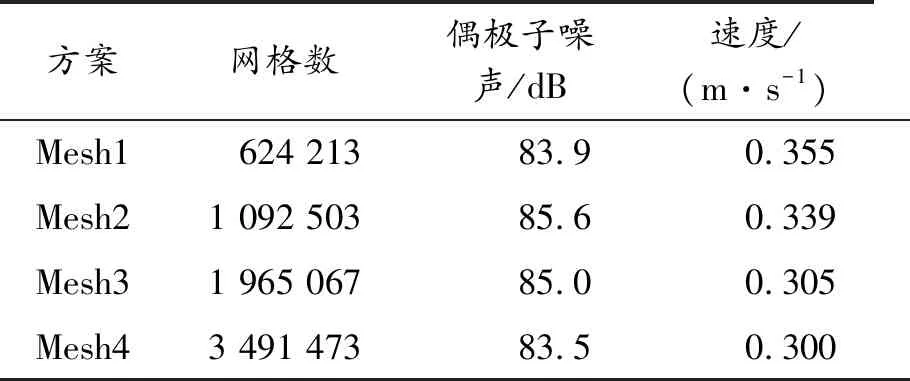
表1 网格无关性验证
2.4 边界条件
入口设置为压力入口,总压设置为0 Pa,出口设置为压力出口,表压设置为0 Pa。风机表面选择旋转壁面,以风机轴为旋转轴,旋转速度设置为风机最大转速2 400 r/min,其余壁面则设置为静止壁面。计算域4部分之间的接触面均设置为“interface”,用于实现数据传递。
3 仿真结果分析
3.1 轴流风机气动噪声分析
3.1.1单风机分析结果
为得到监测点处的噪声声压级频谱曲线,参考相关试验在风机正前方1 m处设置监测点[11]。图6为监测点处的噪声声压级频谱曲线。轴流风机的噪声分为旋转噪声和涡流噪声,其中旋转噪声为离散噪声,在噪声频谱中体现为离散峰值,是由叶片周期性旋转造成的。涡流噪声为宽频噪声,在噪声频谱中体现为平稳宽阔的部分[2,9]。
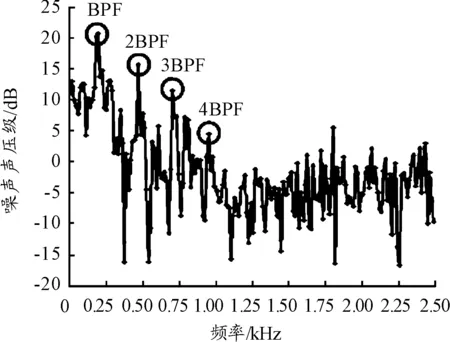
图6 噪声声压级频谱曲线
大量研究表明[2,10-11,19],轴流风机离散噪声一般在基频以及高次谐波处会出现峰值,其中基频处的值在整个频段范围内最大。在转速恒定情况下,叶片等距分布的轴流风机的基频,也叫叶片通过频率(BPF),可用式(9)计算得到[2],基频的倍数称为高次谐波。
(9)
式中:n为风机转速;z为叶片数量。
经计算得,本文所研究风机的基频为240 Hz,从图6可知,在基频240 Hz以及高次谐波480 Hz、720 Hz等频率点处均出现了离散峰值,前四阶峰值较为明显,并以基频处峰值为最高点,随频率增加峰值依次衰减,与上述结论相符。宽频噪声部分随着频率增加逐渐降低且趋于平缓,因此风机的降噪应集中在基频及其前几阶高次谐波处。
参考王宽[8]和范士杰[9]对车用风机的仿真和实验研究,此处仿真未考虑驱动电机以及附件振动的噪声。经仿真得,该风机气动噪声的总声压级为47.7 dB,市场上同类型尺寸风机产品的实测噪声值处于40~50 dB区间,因此仿真结果具有一定的可靠性。
3.1.2带风机罩分析结果
稳态分析结束后,首先激活宽频噪声模型来定位噪声源,得到偶极子噪声分布,如图7所示。图7(a)显示最大的噪声来源位于风机叶片,集中在叶片边缘处,且迎风侧的叶片边缘处噪声强度明显大于另一侧。图7(b)显示风机罩的偶极子噪声主要分布在贴近旋转域处。风机壳体和风机罩之间的间距极小,缝隙大小仅2 mm,气流在此处流动阻力大,风机罩的阻挡使该处易产生大量涡流。该位置又靠近风机罩的出风口,孔口截面积的突变造成出风口流速高,极易产生噪声。
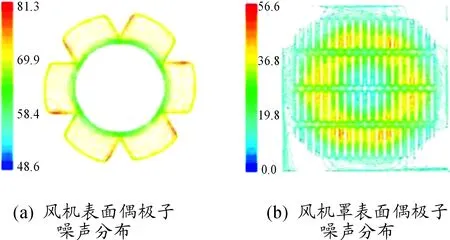
图7 原方案偶极子噪声分布
瞬态分析结束后,在与上文相同监测点处得到的声压频谱曲线如图8所示。加入风机罩后,远场噪声由风机本体以及风机罩两部分噪声耦合而成,噪声的离散峰值,尤其是在基频及其高次谐波处有明显提高,宽频噪声部分也有所提高。经计算得噪声的总声压级从47.7 dB提高为60.8 dB,可见风机罩的存在会带来大量的噪声,需对风机罩进行合理的优化设计,寻求有效的降噪手段。
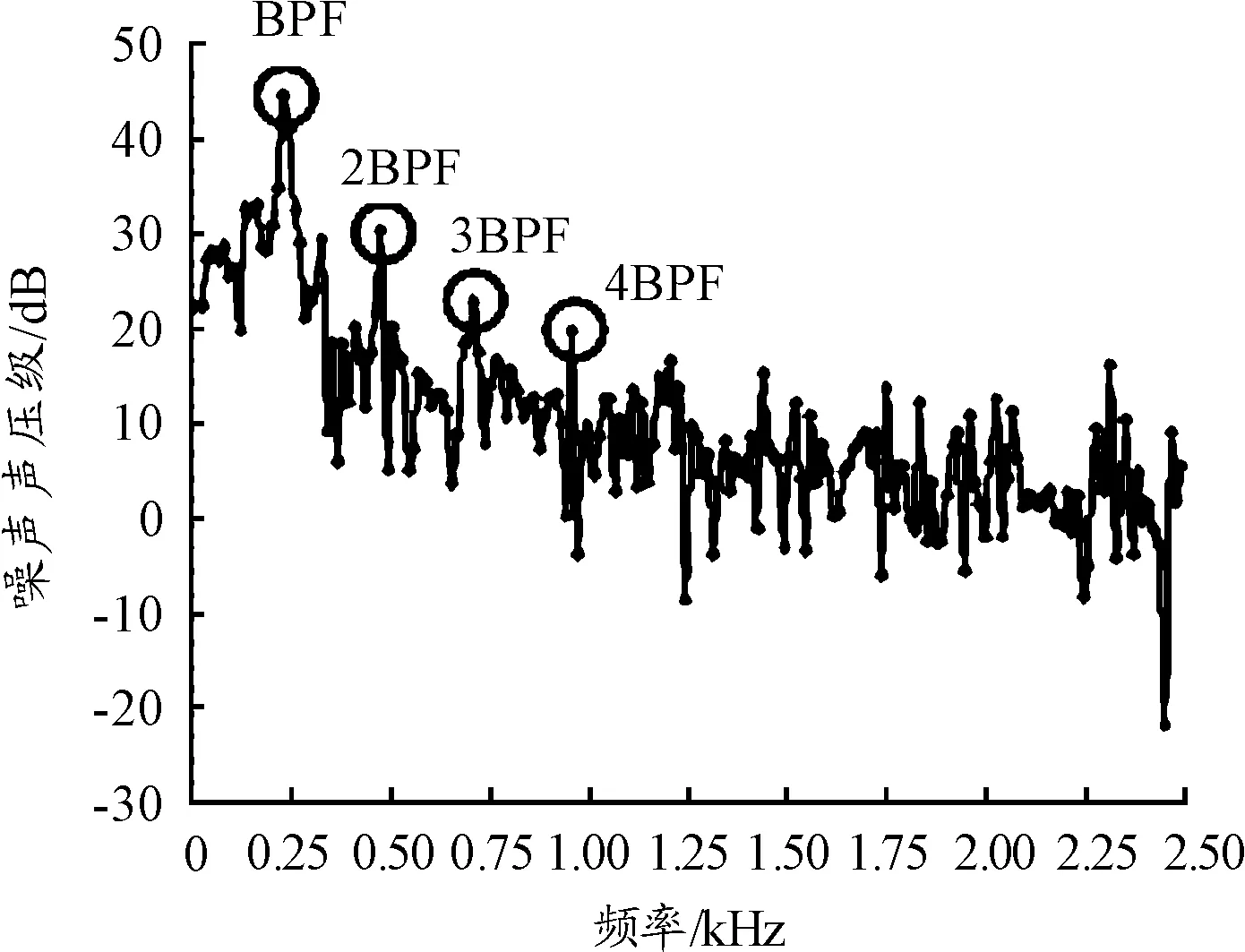
图8 噪声声压级频谱曲线
3.2 风机罩安装距离对噪声的影响
由于风机壳体边缘离风机罩距离过近,造成了该间隙处流动阻力大,流速和压强的变化极为复杂,产生了较大的噪声。为了分析风机罩与风机距离对气动噪声的影响,现调整风机罩的安装距离,调整后的安装距离从5 mm到20 mm,以5 mm为间隔总共形成4种方案。此处采用稳态分析后激活宽频噪声模型的方法,对风机罩表面的偶极子噪声变化规律进行分析,总结出一定的设计规律。
仿真得到4种方案的偶极子噪声分布云图如图9所示。从噪声分布云图可以看出:随着风机和风机罩之间距离的增加,风机罩表面的偶极子噪声值急剧降低,证明安装距离对风机罩表面的噪声强度影响极大。偶极子噪声的分布也随着安装距离增加开始发生改变。间隙加大到一定值后,噪声源不再集中于风机罩贴近旋转域处,逐渐地变为风机罩骨架及各出风口棱边处,此时气流发展充分,从各出风口均匀流出,起主导作用的影响因素是出风口气流流速。
综合来看,调节风机罩的安装距离仍需要考虑实际的安装条件。虽然继续将距离增加,噪声可以得到降低,但是会占据更多的空间,妨碍其他设备的安装,且会影响美观。
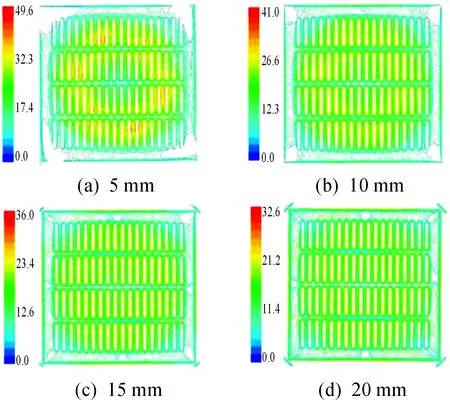
图9 4种安装距离下的偶极子噪声分布云图
3.3 风机罩优化方案
3.3.1改进后风机罩
风机罩的安装位置常受到空间的限制,增加安装距离时常无法实现,对出风口形状进行改进是另一个可行的方案。
经上述分析得,原方案的主要噪声源位置大致分布在风机罩贴近旋转域的骨架位置,该位置的骨架阻碍气流流出,考虑将这一范围内的材料尽可能去除,重新设计的出风口形状为环形,中间加十字形的支撑架。为了减小出风口截面积的突变,在满足开孔处手指无法伸入的前提下,可以适当加大核心出风区域的开孔面积,使气流的流出更加顺畅。环形骨架和中间的十字形支撑架宽度均设置为2 mm,为安全起见,将空隙宽度设置为5 mm。优化设计后的风机罩出风口形状如图10所示。
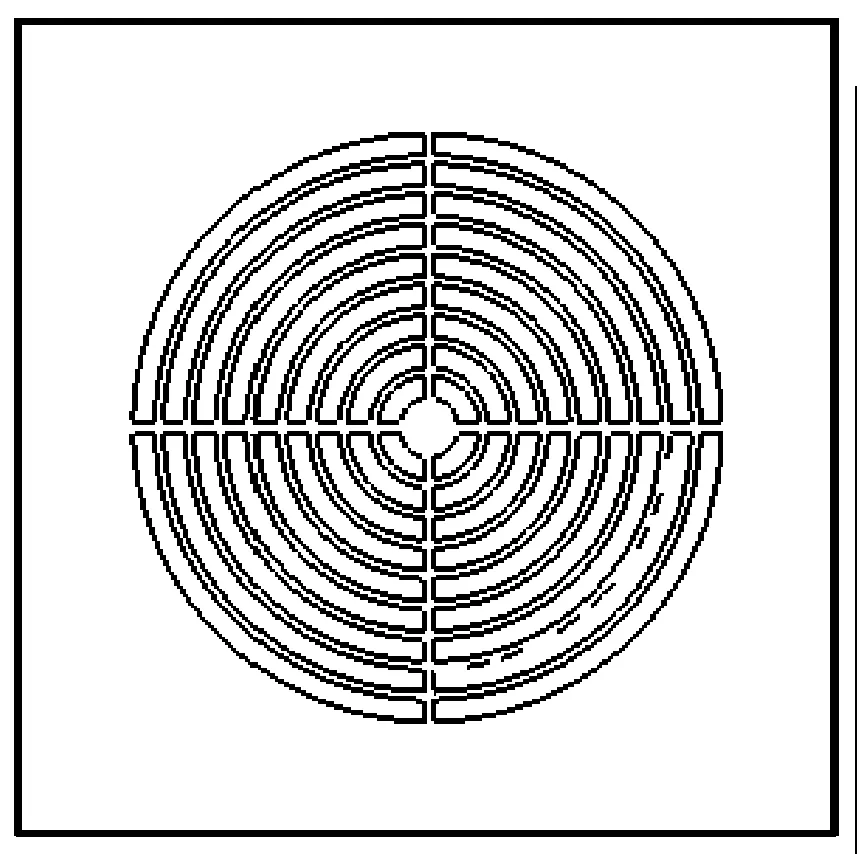
图10 风机罩改进方案示意图
3.3.2气动噪声分析
首先仍进行稳态分析,激活宽频噪声模型观察噪声源的位置变化。改进方案的偶极子噪声分布云图如图11所示,可见偶极子噪声最大值仍位于风机罩贴近旋转域处,但噪声强度有明显衰减。随着核心位置出风面积的增加,出风口处的流速有所下降,使噪声得到一定抑制。
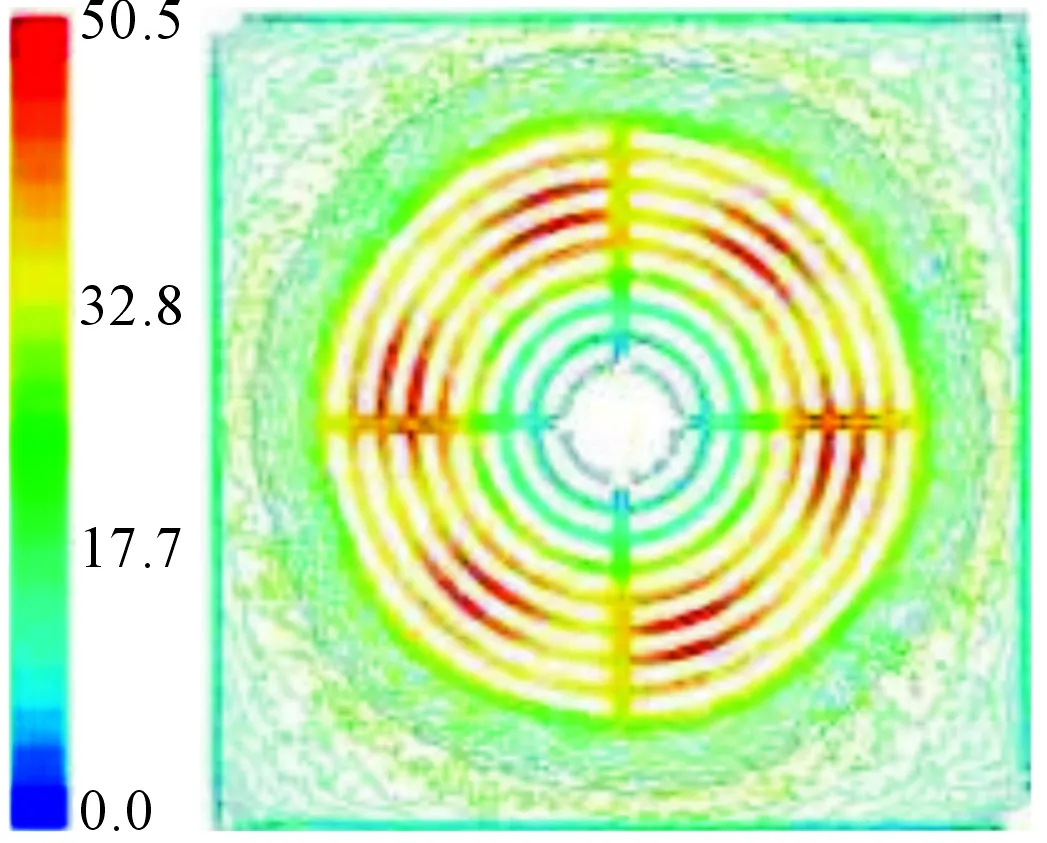
图11 改进方案偶极子噪声分布云图
瞬态分析结束后,在与上文相同监测点处得到的声压频谱曲线如图12所示。与原方案不同的是,出口形状改为环形后,风机本体与风机罩噪声耦合之后的离散峰值最大值并不在风机基频处,而是出现在二次谐波处,类似情形在Hu等[19]的研究中也有提及。不过,各离散峰值处的噪声值均有显著降低,改进方案的噪声总声压级降低为56.7 dB,相比于原方案的60.8 dB,降噪效果较为明显。
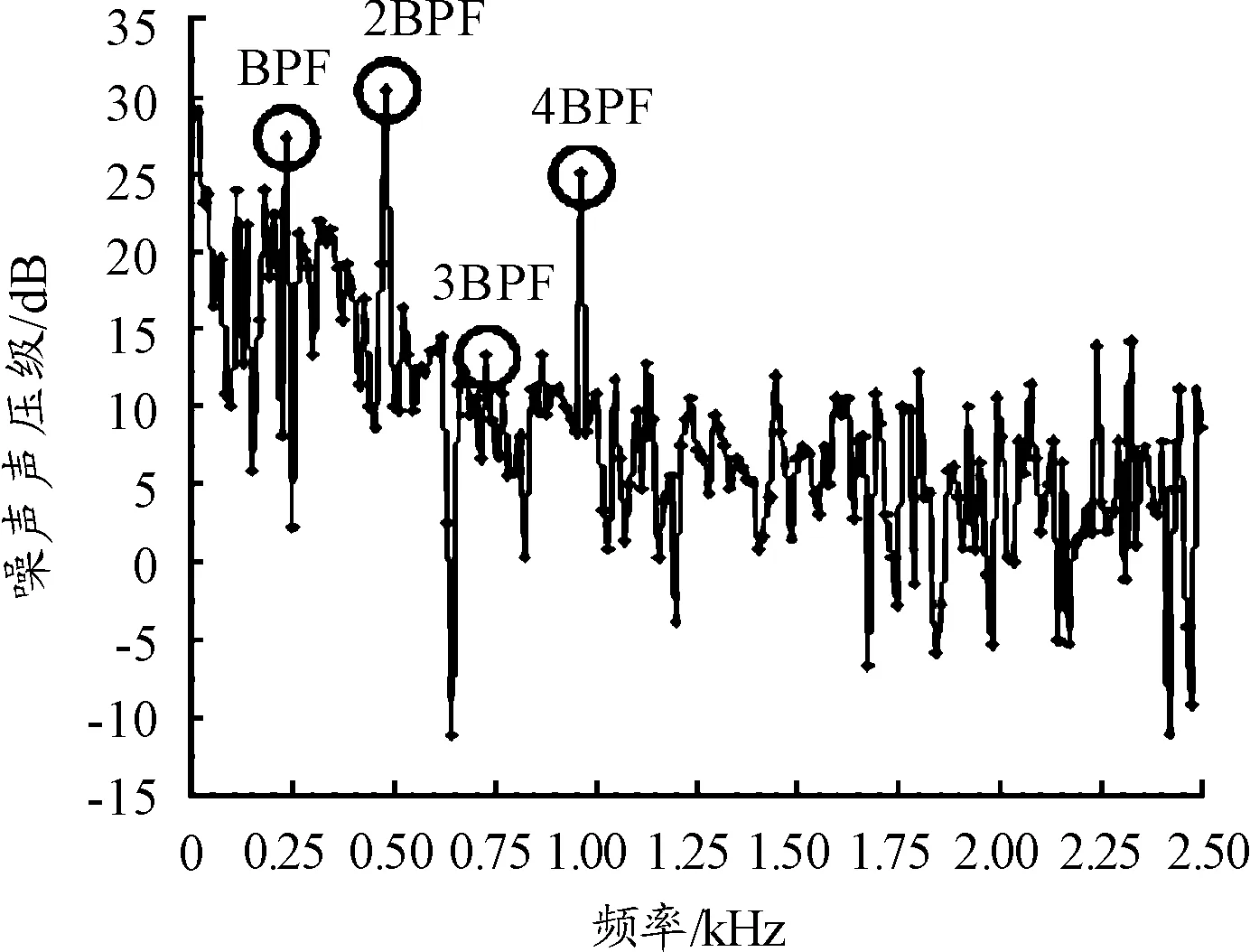
图12 噪声声压级频谱曲线
4 结论
运用计算流体力学和计算气动声学的方法,借助Fluent中的噪声模型来快速评估风机罩表面偶极子噪声贡献,得到风机远场监测点噪声声压级频谱,可以为实际的风机罩结构设计提供有效的指导意见,大大缩短了开发周期。
通过对某轴流风机罩的气动噪声分析可以得出以下结论:
1) 风机噪声主要由离散噪声和宽频噪声组成,离散噪声一般出现在风机基频及其高次谐波处,由叶片周期性旋转产生,通常在基频处取最大值。宽频噪声分布区域较为集中,随着频率的增加逐渐降低且趋于平缓。
2) 风机罩的加入会大大增加风机噪声,其中离散噪声的增加尤为明显。由于风机罩与风机之间间隙极小,气流运动较为复杂,风机罩表面偶极子噪声集中于贴近旋转域处。
3) 随着风机罩与风机之间距离的增加,风机罩表面的偶极子噪声强度显著降低,且分布区域由贴近旋转域处转变为风机罩骨架及各出风口棱边处,此时间隙拉大,气流充分发展,对噪声起主导作用的是出风口处气流流速。但是距离过大时会占据安装空间且影响美观,需要根据实际情况考虑。
4) 风机罩贴近旋转域处是偶极子噪声主要分布区域,应考虑去除这部分材料。环形出风口拥有良好的降噪效果,核心区域的出风面积适当加大,可以降低出风口处气流流速,气流流出也更加顺畅。
