基于热流固耦合的架空管道方形补偿器有限元分析
2019-05-23徐征南牛琦锋林冠堂陈英红
黄 思,徐征南,张 聪,牛琦锋,林冠堂,陈英红
(1.华南理工大学 机械与汽车工程学院, 广州 510641; 2.广东省特种设备检测研究院珠海检测院, 广东 珠海 519002)
化工园区的架空管道一般是数条甚至几十条集中敷设在管廊上,用于输送各种温度、压力和流动工况的化工原料和成品,因而可能出现局部变形、减薄失效等问题,产生安全隐患。为消除温度应力和释放温度变形,管廊上一般设有方形补偿器等补偿装置。近年来有关技术人员对方形补偿器相继开展了研究工作。高勋等[1]介绍了方形补偿器的设计计算和施工安装方法。常守欣等[2]通过热应力分析和验算,给出了补偿器几何尺寸的确定方法。李相通等[3]通过二次应力分析,对2种常用的大型热水锅炉供水管道方形补偿器做了对比计算分析。但目前有关方形补偿器的分析主要还是基于一些常用的设计计算手段,缺乏系统、完善的受力计算及校核评估方法。
本文选取华南地区某化工园区的架空管道方形补偿器作为研究对象,考虑重力、介质温度、流动对管道作用力等因素,建立系统完整的ANSYS有限元计算模型进行热流固耦合数值计算,旨在探索一套针对复杂架空管道实际应用的安全风险评估方法,为架空管道的运行安全提供坚实的技术支持。
1 有限元建模
1.1 几何模型
所研究的架空管道方形补偿器几何模型如图1所示,其纵向和横向具体参数如图2和图3所示。管廊有10组立柱、4层管架。第1层管架有5根管道,第2层有3根,第3层有3根,第4层有16根,一共27根管道,管道编号如图3所示。
1.2 计算单元类型
根据图1~3所示的架空管道方形补偿器布局,建立ANSYS的APDL有限元计算模型。分别使用梁单元(Beam189)和管单元(Pipe289)对管架和管道进行建模[4-10],表1给出了管架和管道单元的具体数据,其中:B为梁单元截面长度;H为截面高度;D为管单元外径;δ为管壁厚度。

图1 架空管道方形补偿器几何模型

图2 模型纵向示意图

图3 模型横向示意图
1.3 材料属性
有限元单元模型中使用的材料参数如表2所示。由结构的材料、单元类型以及单元截面尺寸,建立了完整的架空管道ANSYS计算模型,共包括12 660个单元和25 057个节点。图4为架空管道方形补偿器有限单元网格模型。

表1 有限单元参数

表2 材料参数
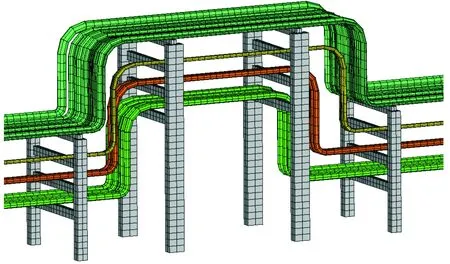
图4 架空管道方形补偿器有限元网格
1.4 介质参数
根据现场实际情况,计算所使用的介质种类、操作工况和介质物性参数,如表3所示。
2 载荷与约束条件
载荷主要有重力、介质温度、流动对管道的作用力。计算中对管道两端和立柱底部采取固定约束。
2.1 介质温度载荷
管道因流动介质温度与安装时环境温度的差异而产生伸缩,因此在有限元计算中,需同时考虑温度和结构的选项[11-15]。施加温度载荷时,所需的材料膨胀系数、介质工作温度和导热系数见表2和表3。
2.2 介质流动载荷
流动介质对管道施加的力主要有因黏性流动造成的沿程阻力和因管道变向90°而产生的作用力[16]。
1) 等径管道沿程阻力
(1)
沿程阻力系数为
(2)
雷诺数表达式为
(3)
其中:l为管道长度;d为管道内径;v为介质流速;υ为介质运动黏性系数;A为管道截面积。如图5所示。

表3 管道输送介质参数
2) 90°等径弯管作用力
FX=(p1+ρv2)A,FY=(p2+ρv2)A
(4)
作用力方向和作用点如图6所示。

图5 作用于等径直管的流体力

图6 作用于90°等径弯管的流体力
3 计算结果与分析
计算结果主要关注架空管道方形补偿器的整体位移和应力分布,水平支撑结构关注最大弯矩和剪力,立柱则关注最大轴力[10]。
3.1 位移分布
图7和图8分别是计算得到的架空管道方形补偿器X向和Y向位移分布。由图可见:最大X向位移(11.4 mm)出现在编号13、输送介质为过热蒸汽的管道,位于管架⑤和管架⑥之间;最大Y向位移出现在编号9、输送介质为非芳烃产品的管道,位于管架⑤和管架⑥之间,最大位移值为10.2 mm。此外,由图7、8可见,方形补偿器两端上圆角处受拉伸,下圆角处受挤压,位移情况与文献[17]对方形补偿器受力变形的分析一致。
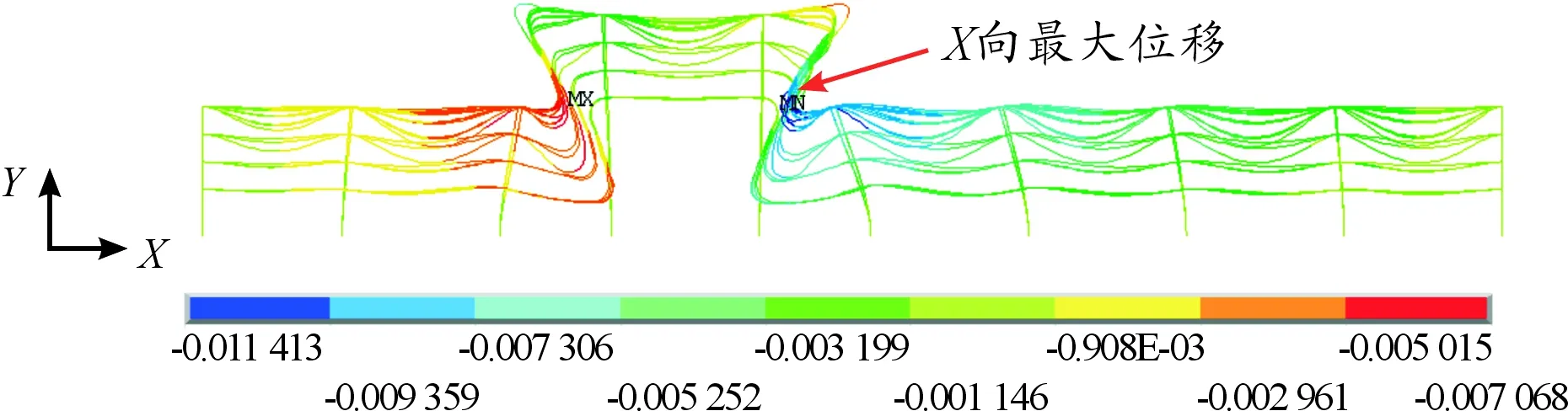
图7 X向位移分布

图8 Y向位移分布
3.2 等效应力分布
图9为计算得到的架空管道方形补偿器等效(Von Mises)应力分布。由图9可见:最大应力(156 MPa)出现在编号13、输送介质为过热蒸汽的管道与管架⑧第4层横梁接触的地方。由于该管道内径小、介质温度高、流速大,所以该管道应力高于其他管道。

图9 等效应力分布
3.3 轴力分布
图10为计算得到的架空管道方形补偿器立柱轴力图。由图10可见,方形补偿器中2个最高的立柱即管架④和管架⑤立柱底部所承受的轴力最大,最大轴力为629.66 kN。

图10 立柱轴力分布
3.4 剪力分布
图11为计算得到的架空管道方形补偿器的剪力图。由图11可见:管架横梁的最大剪力为311.63 kN,出现在管架⑥第4层横梁与管道12连接的位置;管道的最大剪力为202.23 kN,出现在输送介质为原油的管道12上。这说明横梁和管道的最大剪力都出现在由高向低过渡中较低管架的横梁上或连接处。

图11 剪力分布
3.5 弯矩分布
图12为计算得到的架空管道方形补偿器弯矩分布。由图12可见,管架横梁的最大弯矩为311.88 kN·m,出现在管架⑤和⑥第1层横梁与管道1的连接处;管道的最大弯矩为129.63 kN·m,出现在输送介质为原油的管道12上。这说明横梁和管道的最大弯矩都出现在由高向低过渡中较低管架的横梁上或连接处。
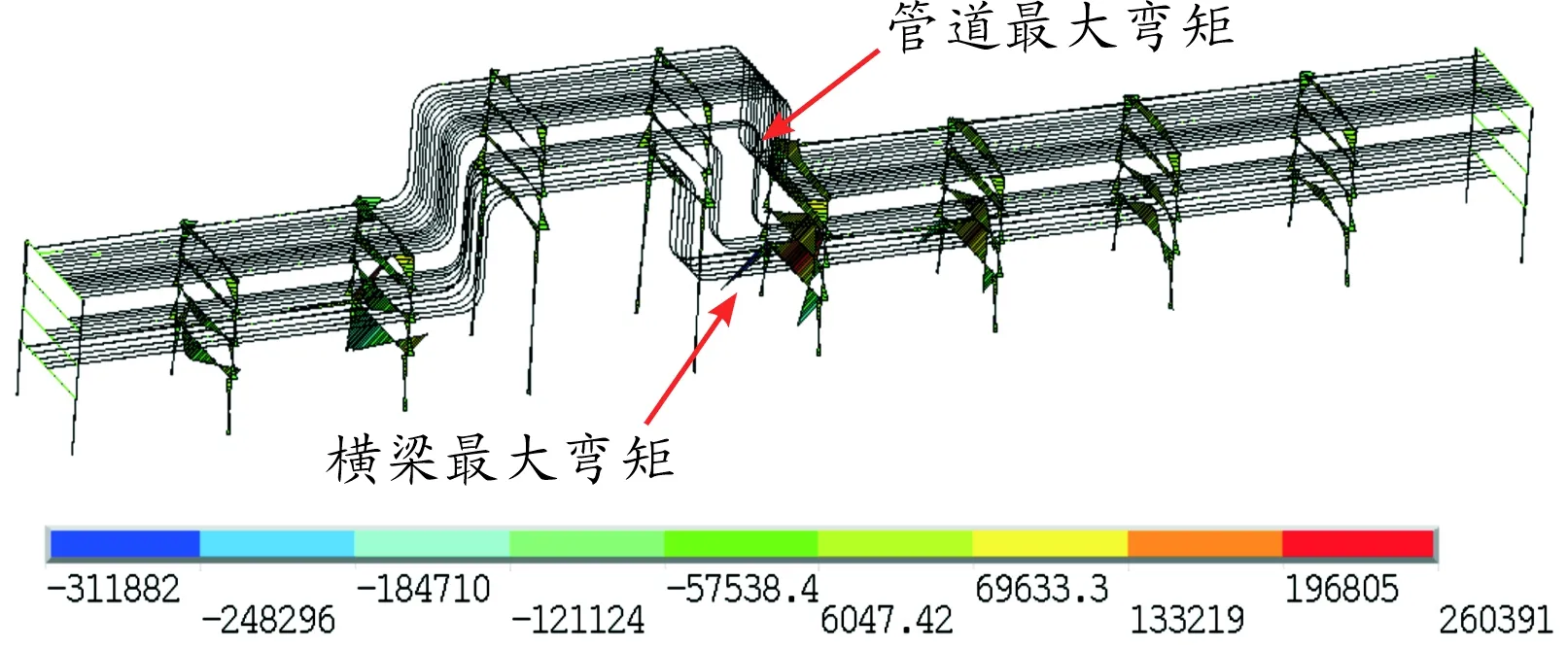
图12 弯矩分布
4 管道强度校核
根据行业的技术规程[18]可知,由热胀冷缩和其他位移受到约束而产生的热胀二次应力σf需要满足式(5)的条件[2]。
(5)
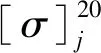
由图9可知,计算得到的架空管道方形补偿器最大应力为156 MPa,满足σf≤183.4 MPa的条件,也低于20#钢的屈服强度225 MPa,故该在役的架空管道方形补偿器运行可靠。
5 结论
1) 所研究的架空管道方形补偿器最大位移出现在2个最高立柱之间,两端上圆角处受拉伸,下圆角处受挤压,位移情况符合设计要求。
2) 方形补偿器中的最高立柱底部承受轴力最大。管架横梁的最大剪力和弯矩出现在管架由高向低过渡的低管架横梁;管道的最大剪力和弯矩则出现在与高低管架之间较低管架的连接处。
3) 在整个架空管道方形补偿器中,最大应力出现在内径小、介质温度高、流速高的管道与横梁接触的位置。经强度校核,现有研究模型满足设计要求。
4) 所采用的热流固耦合有限元计算方法对实际中复杂的架空管道方形补偿器受力分析是切实可行的,可为在役架空管道的运行安全提供坚实的技术支持。
