基于夏氏最小二乘的轨道控制力系数辨识

王西京袁博孔大林卞燕山

1. 西北工业大学 航天学院, 西安 710072 2. 航天器在轨故障诊断与维修重点实验室,西安 710043 3. 西安卫星测控中心, 西安 710043

航天器长期在轨运行，存在轨道摄动、初始状态误差、控制误差等因素，使得实际轨道偏离标称的设计轨道，不能完成预定任务[1-2]。为使卫星长期运行在理论设计的标称轨道上，以及满足卫星用户新的应用需求，需要对卫星实施轨道机动。随着卫星组网、编队、交会对接、天地往返等多种主动变轨控制技术的日益成熟，以及空间目标碰撞规避次数的增加，还需要通过卫星轨道控制完成更复杂的空间任务[3]。

卫星轨道控制推力器推力是以推进剂贮箱压力为自变量的多项式函数，其系数为装订常数，在卫星的整个寿命期保持不变[4-5]。随着卫星轨控次数的增加，推进剂贮箱压力不断降低，以理论推力为基础计算的卫星速度增量与实际速度增量出现误差，导致轨道控制精度降低。传统的轨道控制速度增量计算以前一次推力器标定系数作为计算依据[6]，并且推力系数维持不变[7]，没有有效利用历次轨道控制数据进行优化计算，导致理论速度增量与实际速度增量误差不可测，给轨道控制策略制定带来了一定困难。

本文统计分析在轨管理的典型航天器平台及其发动机的轨道控制历史数据，分析轨道控制理论和在轨控制数据拟合建立轨道控制经验模型，用当前可测量的系统输入和输出预测系统输出的未来演变，得到不同工作情况下实际轨道控制误差与控制参数及其他主要影响因素之间关系的经验公式，为轨道控制策略决策提供参考。选取轨道半长轴控制量300 m以上和300 m以下的两类近地卫星，对其轨道控制历史数据进行分析，经实际数据测试，采用夏氏改良法进行推力系数拟合后预测的速度变化量精度较高。

1 最小二乘夏氏改良法

最小二乘法的特点在于系统的输入和输出信号反复过滤。夏氏法是一种交替的广义最小二乘法求解技术，由夏天长(T.C.Hsia)提出来的，它不需要数据反复过滤，因而计算效率较高。这种方法能够克服最小二乘估计中的有偏估计问题，而且由这种方法所导出的计算方法也比较简单，分为夏氏偏差修正法和夏氏改良法[8]。

当考虑系统噪声影响时，系统的差分方程可表示为：

(1)

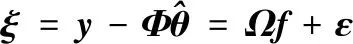
(2)

求式(2)中f的最小二乘估计:

(3)

于是有

(4)

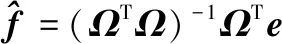
这种算法称之为夏氏改良法，夏氏改良法改进了收敛效率，工程上可用。

2 控制力系数辨识模型

根据动量与冲量之间的关系可得[9]：

(6)

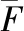
(7)

式中：F为轨控前推力；Ff为轨控后推力。

(8)

式中：Di(i=1,2,3,4)为拟合多项式系数；P为轨控前储箱压力(Mpa)；Px为储箱1、2当前推进剂密度(kg/cm3)；Pf为轨控后储箱压力，脚标x代表燃料储箱编号(x=1，2)，推力器工作时储箱1和储箱2根据压强变化互相切换[10]，

(9)

式中：VTx为储箱容积；

ρx=1025.5-0.875×(Tx-273.15)

mx为燃料剩余质量，

ISx为比冲与压力的关系，

IEx为本次机动推力器所需提供压力所对应的总冲[11]，

其中卫星当前质量

msat=msat0-m01+m1-m02+m2

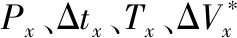
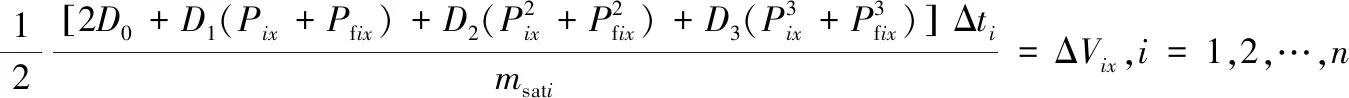
式中：i代表第i组测量值。

将式(10)展开后可得到：

(11)

根据式(11)，可得到测量矩阵Φ、待求参数向量θ、输出向量y：

θ=[D0D1D2D3]T

y=[ΔV1xΔV2x… ΔVnx]T

考虑系统噪声ξ影响时，定义噪声拟合系数f=[f1f2f3f4]T，系统噪声ξ的拟合公式为：

(12)

噪声ε为不相关的随机序列，故可用最小二乘法得到系数f的一致无偏估计[13]。若有n组测量数据，考虑到计算效率，采用最小二乘夏氏改良法[14]，则有

(13)

式中：e为残差；Ω的具体表达式如下：

综上，参照最小二乘夏氏改良法的迭代计算步骤即可求得估计系数[15]。

3 仿真验证

轨道控制半长轴300 m对应的速度变化量约为0.15，在工程经验上Δa=300 m为分界线，推力稳定性和保持环会有差别。轨道高度低的卫星轨迹保持环小，保持周期短，控制量大；轨道高度高的卫星轨迹保持环大，保持周期长，控制量小。所以分别选取轨道半长轴控制量300 m以上和300 m以下的两类近地卫星，对其轨道控制历史数据进行分析，得到的结论具有普遍性。

3.1 算例一

选取轨道高度300 km以上某低轨卫星共44批次控制数据计算推力拟合系数，其中前20批次轨控使用贮箱1推进剂，后24批次轨控使用贮箱2推进剂，相关仿真参数如表1所示。

综上，可使用数据共44组，每次仿真去掉其中一组数据，用余下43组数据作为样本，去掉的那组数据作为精度验证标准，进行仿真，仿真结果如图1所示。

图1为理论速度变化量、预测速度变化量与标定速度变化量，其趋势几乎一致。对预测误差百分比取绝对值，统计可得其误差百分比分布。以标定速度变化量为近似真值，分别计算理论误差和预测误差，统计可得其相对误差百分比分布如图2所示，最大误差为4.6%，平均误差为1.39%，采用夏氏法进行推力系数拟合后预测的速度变化量精度较高。

表1 仿真参数

图1 速度变化量分布Fig.1 Variation distribution of velocity

图2 误差百分比分布Fig.2 Percentage distribution of error

3.2 算例二

选取轨道高度300 km以下某低轨卫星共13个批次控制数据计算推力拟合系数，由于算例二所选卫星的实测轨控数据样本偏少，且可直接提供轨控后的贮箱压强，因此在估算模型中无需再重新计算轨控后贮箱压强，直接代入即可。相关仿真参数如表2所示。

综上，可使用的数据共有13组，每次仿真去掉其中一组数据，用余下的12组数据作为样本，去掉的那组数据作为精度验证标准，进行仿真，仿真结果如表3所示。

对上述预测误差百分比取绝对值，统计可得其误差百分比分布如图3所示。

表2 仿真参数

表3 仿真结果

从表3和图3可以看出，最大误差为1.61%，平均误差为0.85%，采用夏氏法进行推力系数拟合后预测的速度变化量精度较高。

参考第8～13次控制前的轨道参数(见表4)，将预估的速度增量代入轨道仿真模型中，进行仿真得到的结果与实际轨控后的半长轴对比如表5所示。

从表5的统计结果可以看出，所修正后的控制系数计算得到的速度增量代入轨道外推模型，得到的半长轴与实际半长轴对比都小于20 m，最大误约19 m，最小误差仅1.6 m。

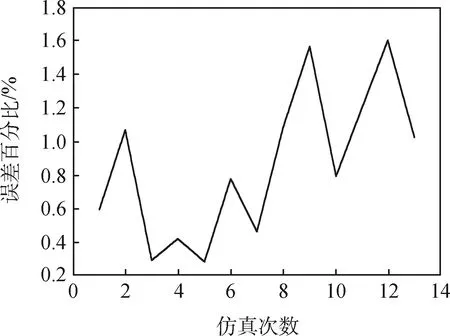
图3 误差百分比分布Fig.3 Percentage distribution of error

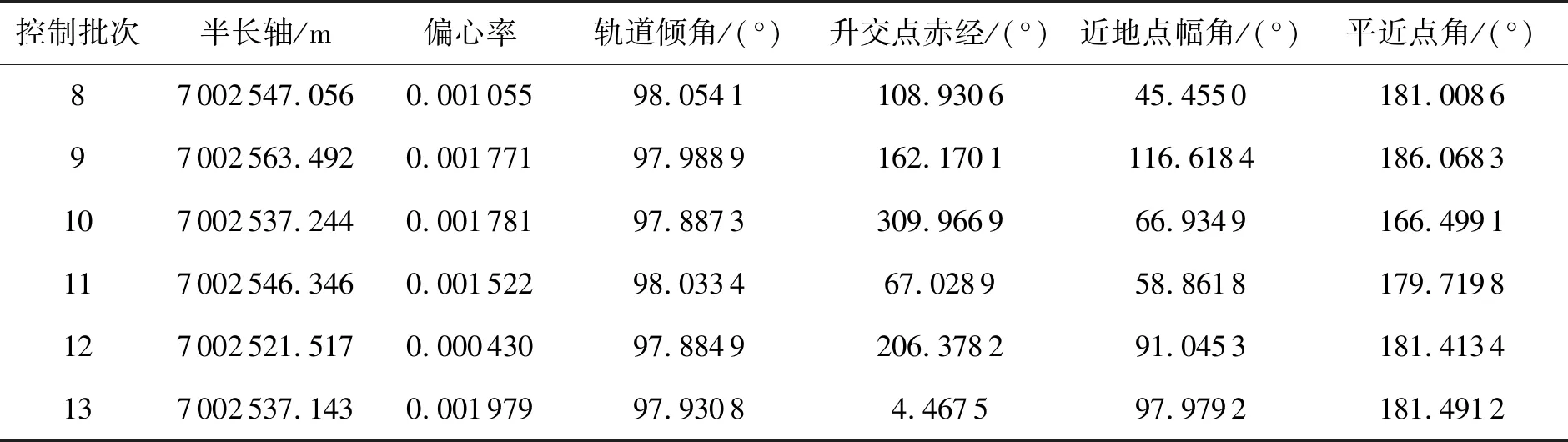
表4 初始仿真参数

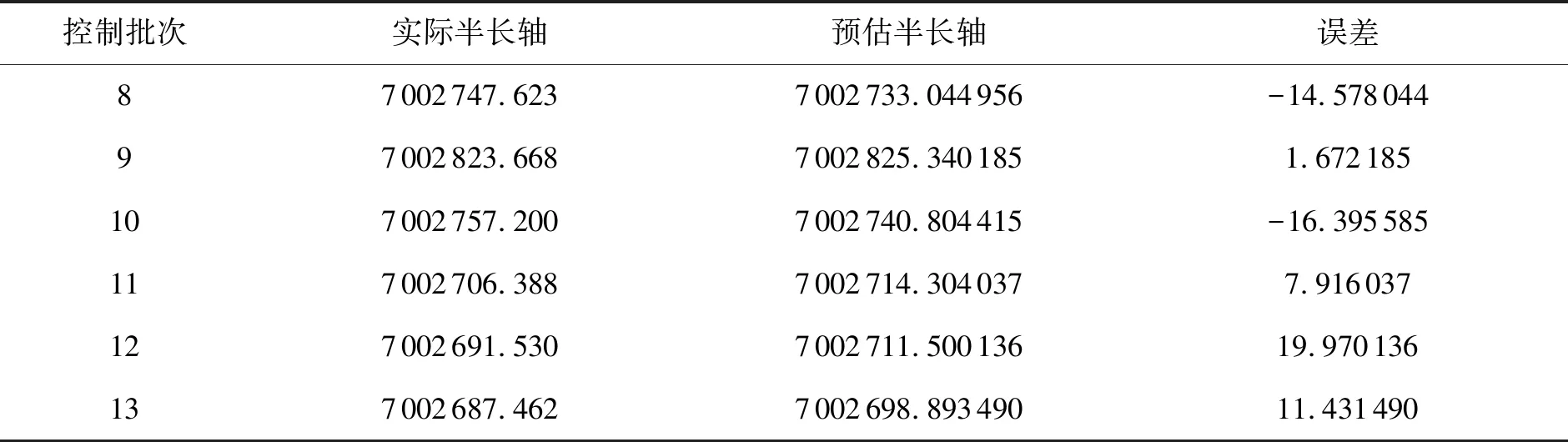
表5 仿真结果对比

4 结束语

通过分析历次轨控理论速度变化量、实际速度变化量、推力器推力持续时间、轨控推力系数之间的相关性，采用最小二乘夏氏改良法估计表征推力的拟合系数，并运用夏氏法进行求解，建立一个能模仿推力器在轨工作情况的模型，用当前可测量的系统输入和输出预测系统输出的未来演变，具有预测精度高的特点，且整个计算过程不涉及标定系数，可以降低主观因素的影响，对轨道控制实施具有参考意义。