基于深度学习的航天器组合体惯性参数在轨智能辨识

南京航空航天大学 航天学院 微小卫星研究中心，南京 210016

近年来随着深度学习理论体系日趋完善，人工智能技术应用于越来越多的领域，但针对航天领域的深度学习应用目前还处于探索阶段。这是因为航天活动相比一般工业生产，场景比较单一，且个体差异性较大，数据积累有限，机器学习深度有限。但随着商业航天的蓬勃发展，人类进入空间越来越多，人工智能在航天的应用有了一个契机。

通过对近年来各个国家航天任务的分析发现，空间在轨操作活动日益增加，如德国的DEOS项目[1]、美国的FREND项目[2]和中国神舟9号与天宫一号对接，航天任务已从过去单一航天器向在轨组合航天器发展，场景日益复杂，数据大量产生。这为深度学习的应用提供了基础。在轨服务过程中的航天器组合体质量、质心位置、惯量矩阵在轨辨识是航天器姿轨操控的基础。这些多参数的在轨辨识，本质上是一个动态寻优过程。借助深度学习在参数寻优上的优势，可以通过特征提取来辨识组合体质量、质心位置和转动惯量等参数。

目前国内外有很多学者针对航天器惯性参数辨识进行相应研究。文献[3]提出了基于Adaline神经网络的航天器惯性参数辨识，通过改进LMS准则来解决神经网络辨识过程中陷入局部最小的问题，其实质上还是对传统BP神经网络的一个改进。文献[4]提出了一种两步辨识航天器转动惯量的方法，第一步针对航天器转动惯量比进行辨识，第二步基于辨识得到的转动惯量比，利用陀螺信息结合最小二乘法得到转动惯量的值，但未能分析初始值对仿真结果精度的影响。文献[5]提出了两种惯量辨识的方法，第一种是基于角动量守恒和整星零动量原理，利用反作用飞轮和陀螺，用最小二乘法实现转动惯量在轨辨识;第二种利用自适应控制方法实现对组合体的惯量估计，虽然该方法能实现姿态稳定状态下对惯量结果的估计，但精度较差。文献[6]基于机械臂运动实现对组合体航天器的全惯量辨识，但在数据仿真中未加入外界干扰因素。文献[7]提出了一种基于QR分解的递推最小二乘法，利用空间机器人基座姿态无扰控制过程中的数据实现对全部惯性参数的辨识。文献[8]提出了开环辨识和闭环辨识两种方法，闭环辨识是在开环辨识上再加闭环控制器实现在姿态稳定下对转动惯量的辨识。文献[9]提出了一种无陀螺航天器质量特性估计算法，利用CMOS-APS跟踪器，设计了含姿态和无姿态估计算法。文献[10]提出了一种基于PAST算法的时变惯量参数的辨识，利用姿态信息和振动信号解算系统状态参数。文献[11]针对实际地面气浮台系统，提出了一种无需外界冲击，依靠安装于气浮平台的立方星振动辨识整个系统动力学参数的方法。文献[12]提出了一种针对目标动量未知的情况下的惯性参数分布辨识算法，算法能够保证在辨识过程中基座姿态稳定。

以上文献所提到的辨识方法都有一个局限性，其辨识基本原理都基于动量守恒定理，即都假设航天器不受外力和外力矩影响，但实际上外力普遍存在，且需要预先对航天器进行动力学建模。目前神经网络在航天中的辨识应用主要集中于传感器和执行器的精度和寿命预测[13-15]。深度学习常用的方法有卷积神经网络、受限玻尔兹曼机、自动编码器、深度信念网络和循环神经网络，目前主流的深度学习框架有Caffe，TensorFlow，CNTK等[16-19]。CNN神经网络是一种深度学习下的神经网络，目前大量应用于图像识别[20-22]，侦测[23-24]和分割[23]，其具有局部视野与权值共享的特点，适用于大数据与特定特征提取的场景。基于此特性，本文提出一种基于CNN深度学习神经网络的航天器在轨惯性参数辨识方法，该方法考虑组合航天器受外力和外力矩不为零的情况，通过对航天器基础动力学的推导，从状态数据中就可辨识组合航天器的质量、质心和转动惯量。

1 CNN神经网络对质量/质心位置的辨识

1.1 组合航天器线动量模型建立

不失一般性，假设航天器组合体之间为刚性连接，组合航天器为刚体。大多数情况下，组合体航天器所受的合外力一般不为零，这里既有自身推力作用，又有环境干扰力的影响。整个航天器组合体的线动量表达式如下：

P=PS+PT=P0+Ft(1)

式中：P为组合航天器总线动量；PS为服务航天器的线动量；PT为目标航天器的线动量；P0为组合体初始状态线动量，假设在捕获瞬间系统线动量守恒，由于目标航天器自身具有线速度，所以系统初始线动量为未知量；F为组合航天器所受的外力的合力；t为组合航天器控制周期。

假设航天器测量的速度为相对于地心惯性坐标系的速度，如图1所示，pS，pT，pC分别为服务航天器质心、组合航天器质心和目标航天器质心在惯性系下的矢量；rS，rT分别为服务航天器质心和目标航天器质心在惯性系下相对于组合航天器质心矢量；vS，vC，vT分别为服务航天器质心、组合体质心和目标航天器质心相对惯性坐标系的速度。由于组合体为刚体，根据速度之间的牵连关系可得出下列关系式。

(2)

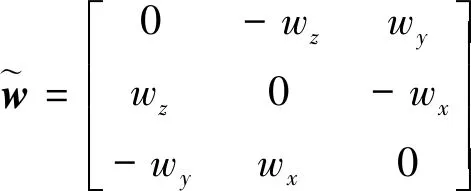
(3)

服务航天器和目标航天器的线动量可分别表示为：

(4)

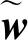
将式(4)代入式(1)得到组合航天器线动量守恒表达式。

(5)

式中：P0为初始时刻系统线动量，可以写为：

P0=mSvS0+mTvT0(6)

式中：vS0，vT0分别为初始时刻服务航天器与目标航天器的线速度。

将式(3)代入式(6)可得：

(7)

将式(7)代入式(5)：

Ft=mS(vS-vS0)+

(8)

将式(8)写成与辨识时间相关量：

(9)

从图1分析可知，在惯性系下pT-pS等于rT-rS，将式(9)通过移项可得：

式中：A矩阵中的量都可通过服务航天器传感器测量获得为已知量。整个方程中所需辨识的量为mT和rT-rS，从图1可以看出，rT-rS为服务航天器质心指向目标航天器质心的矢量。上述参数辨识的过程实际上是线性方程求解的过程。

1.2 质量/质心位置辨识误差分析

辨识的误差主要由两部分构成：1)外界环境扰动力；2)速度测量误差。所以式(10)在考虑误差后可写成：

(11)

其中：

假设只存在外界干扰力，速度和角速度测量不存在误差，则式(11)可写成：

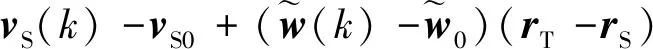
式中：t为组合航天器控制周期。将式(12)通过移项推导可得：

(13)

式(13)右边第二项为外界环境扰动力对目标质量辨识产生的影响，即

ΔmT=f(ΔF)=

(14)

从式(14)可以看出，质量辨识误差和干扰力矩累积量成正比；并且在干扰力矩确定的情况下，卫星速度越大，质量辨识误差越小。

假设只有速度误差，式(11)可写为:

vS(k)-vS0+ΔvS(k)+ΔvS0(k)+

(15)

将式(15)写成式(13)的形式:

(16)

式(16)右边第二项即为速度测量误差所引入的辨识误差。

ΔmT=f(ΔvS)=-

(17)

从式(17)可以看出，质量估计误差与速度测量误差成正比，卫星质量越大引起的质量估计误差越大。

假设只有角速度测量存在误差，式(11)可写成：

(18)

将式(18)结合矩阵求逆公式

(A+B)-1=Α-1-(A+B)-1BA-1(19)

可得：

(20)

式(20)右边第二项即为角速度测量误差所引起的目标相对服务航天器质心位置辨识误差。

(21)

式(21)即为质心位置辨识误差公式，可以看出，在场景确定的情况下，质心测量偏差与角速度测量误差相关，但不是线性关系。

综上公式推导过程，根据式(14)和式(17)，可得出在质量辨识过程中总误差公式：

ΔmT=f(ΔF,ΔvS)=

(22)

从式(22)中不难发现质量辨识的精度取决于外界干扰力和速度测量误差，并且提高卫星速度可以有效降低质量辨识误差。

1.3 质量/质心位置辨识CNN神经网络设计

从上述分析可以看出，质量和质心位置的辨识实际上是一个多元方程求解的问题，通过激励获得多组参数从而进行多参数求解优化的过程。由此可以引入擅长数据学习的人工智能CNN神经网络，进行训练求解。CNN神经网络相比传统神经网络具有参数共享和局部感知的特点。如卫星惯性参数在短时间内是常量，因此可以作为共享参数，利用CNN神经网络参数共享的特点，通过对航天器状态信息学习，就可求取该特征参数。

由于实际航天器组合系统通常是非线性系统，因此需要在CNN神经网络输出端引入激活函数用来加入非线性因素。常用激活函数主要有Sigmod，tanh，Relu等，其函数曲线如图2、图3和图4所示。Sigmod激活函数只保留正向输出特性，而航天器状态信息存在负值，所以该激活函数不适用于参数辨识；tanh激活函数保留了正负输出特性，但其在输入绝对值大于2的情况下会达到饱和，丢失数据中的特征信息；Relu激活函数也只保留正输出特性，当输入为负数时极易造成神经元坏死。通过对上述函数的分析，选择tanh函数作为输出激活函数。

组合航天器线动量在惯性系下较大，这会导致在tanh激活函数下卷积神经网络输出数据都为±1，卷积神经网络无法辨识出质量和质心位置信息。为了能够准确辨识出质量和质心位置信息，本文提出增量的形式对卷积神经网络进行设计。

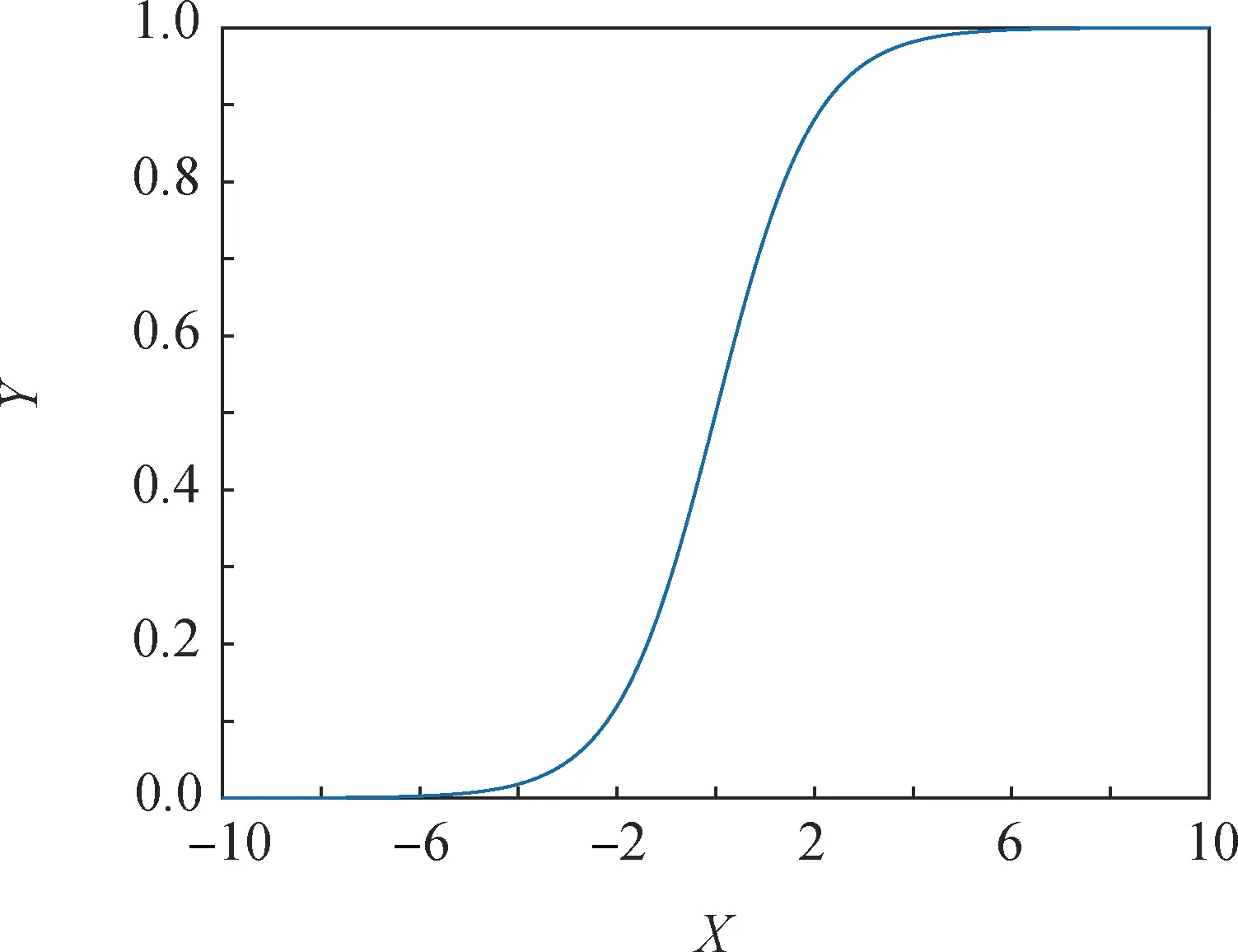
图2 Sigmod函数Fig.2 Sigmod function

图3 tanh函数Fig.3 tanh function

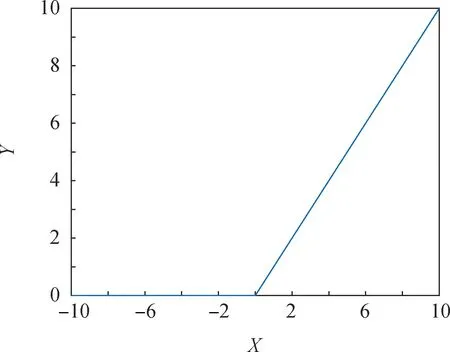
图4 Relu函数Fig.4 Relu function

对式(10)等式左边的A和等式右边的量在前后两个时刻做差，得到线动量增量和线速度增量之间的关系，可用下式表达：

(23)

式中：带有Δ的量表示增量。

卷积神经网络卷积核具有权值共享的特点，辨识mT和rT-rS转换为确定卷积神经网络权值的问题。根据式(11)设计如图5所示的卷积神经网络。

该卷积神经网络分为4层：输入层、卷积层、采样层和输出层。输入层为6×4×N的一个三维矩阵，将传感器获取的数据按特定格式存储在该三维矩阵中用于对卷积神经网络进行训练。卷积层的卷积核为所需要辨识的量mT和rT-rS，该层卷积层的激活函数选用线性激活，最大程度地减少中间过程数据的损失。采样层采用平均采样方式，采样核为2×1的矩阵。输出层为速度在三轴方向上的分量，该层激活函数选用tanh函数保留输出数据的正负特性。

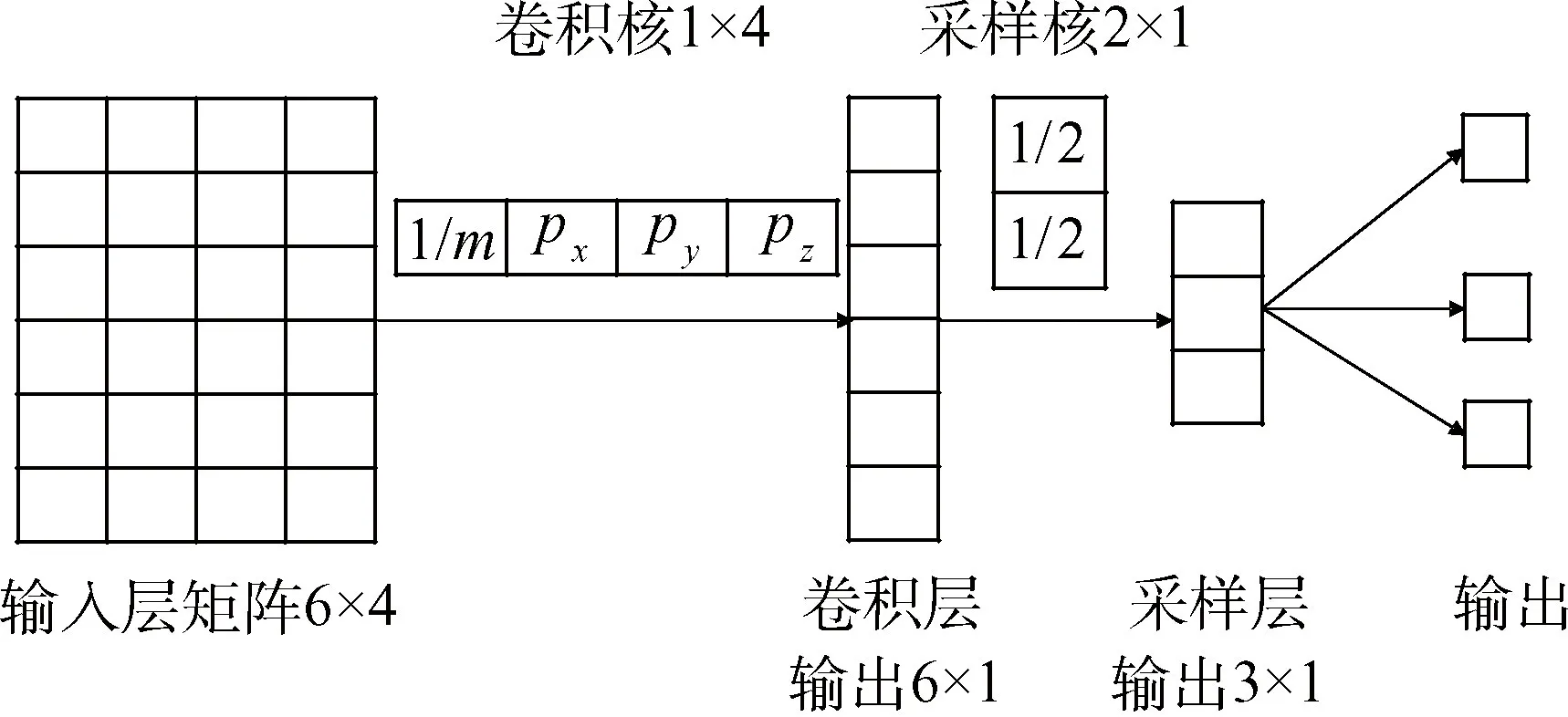
图5 质量/质心位置卷积神经网络Fig.5 Mass/centroid position convolution neural network

2 CNN神经网络对惯量的辨识

2.1 组合航天器角动量模型建立

假设组合体所受外力矩不为零，其角动量公式如下:

(24)

式中：L0为初始角动量，由于目标航天器自身具有角速度，所以初始角动量为未知量；T为组合体主动激励所受外力矩；t为组合航天器控制周期；w为组合航天器相对其质心的角速度，可由星载传感器测量获得；IC为组合体转动惯量，是待辨识量；Δw为组合体在外部激励T下作用时长t后所产生的角速度增量。

分析式(24)可知，角动量公式需要获取前后两个控制周期间的角速度，且组合体初始时刻的角速度可由服务航天器的角速度测量获得。式(24)可写为如下形式：

(25)

式中：L(k)为k时刻组合体角动量；T(i)为各时刻的主动激励力矩；w(i)为i时刻的角速度，可由传感器测量获得；w0为组合体形成瞬间服务航天器测量的角速度；IC为组合体转动惯量，为待辨识量。为了便于观察，将式(25)写成另一种形式：

(26)

式中：

矩阵元素与式(25)相同。

2.2 惯量辨识误差分析

惯量辨识误差来自两部分：1)外界干扰力矩；2)角速度测量误差。对式(26)加入误差量可写为：

(B+ΔB)·

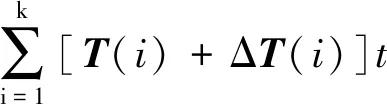
(27)

式中：ΔB为角速度误差矩阵；ΔT为外界干扰力矩。各干扰源之间不存在相互耦合的关系，所以可单独进行分析。

对式(27)进行控制变量分析，设只有角速度测量有误差，则式(27)可写为：

(B+ΔB)·

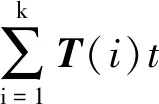
(28)

对式(28)进一步移项可得：

(29)

式中：ΔI即为角速度测量误差所带来的转动惯量辨识误差。从式(29)可以看出，组合体惯量辨识误差与角速度测量误差有关，但其关系较为复杂，不是线性关系。

当只有外界干扰力矩时，式(27)可写为：

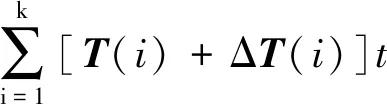
(30)

与不存在干扰的辨识公式做差，可得到外界干扰力矩对转动惯量辨识的影响公式：

(31)

从式(31)中可以看出，当存在外界干扰力矩时，控制周期越长，惯量误差越大，且是一个和力矩相关的累积量。

综合式(29)和式(31)可得惯量辨识误差公式:

ΔI=f(ΔB,ΔT(i))=

(32)

2.3 转动惯量辨识CNN神经网络设计

根据式(24)建立卷积神经网络，如图6所示。

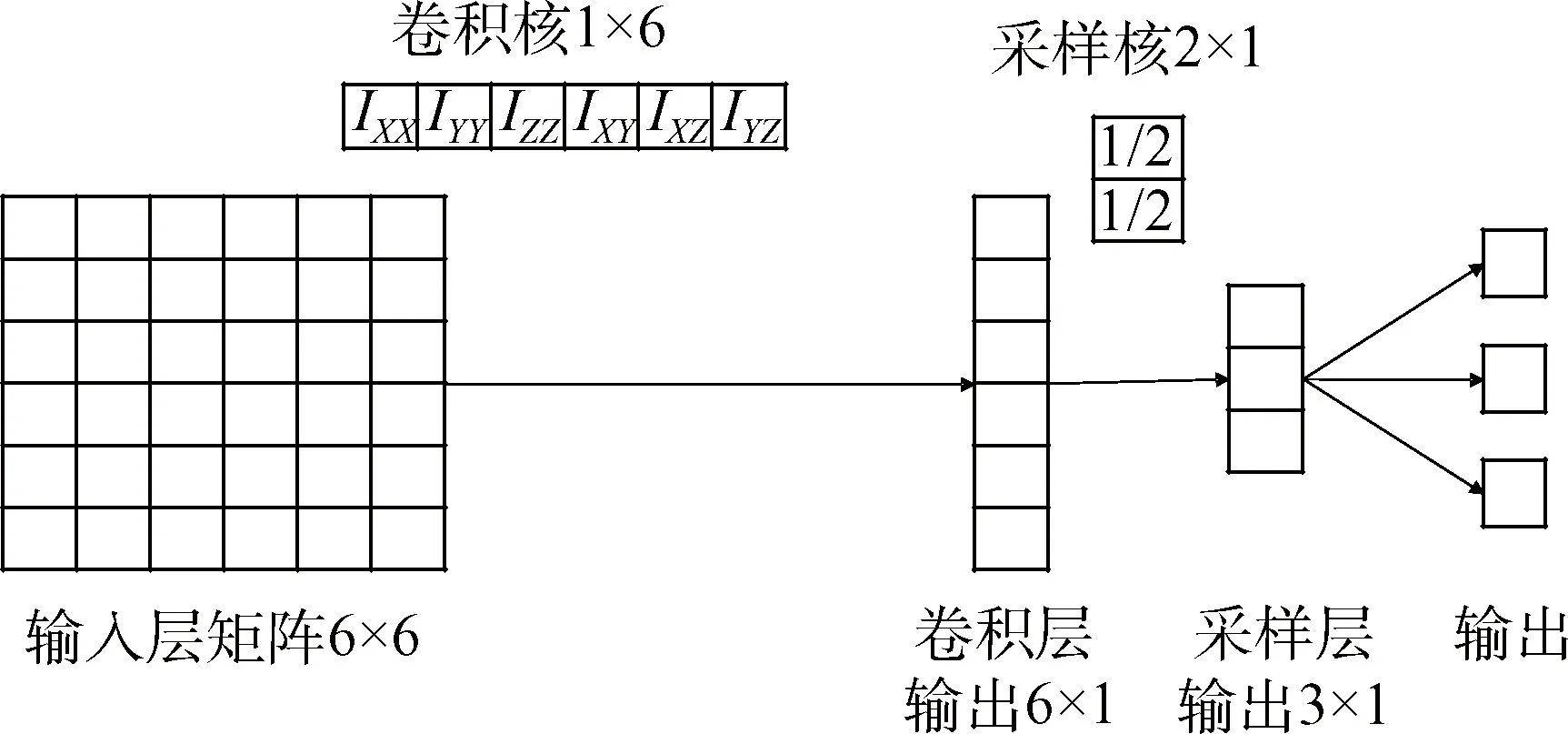
图6 转动惯量辨识卷积神经网络Fig.6 Rotational inertia identification convolution neural network

根据所需辨识参数数量和方程的输入输出参数，设计卷积神经网络输入层为一6×6×N的三维矩阵，卷积完成后采用平均采样方式，每个输入矩阵对应3个输出，输出激活函数与质量/质心位置辨识相同，采用tanh激活函数限制输出在一定范围内且保留原始输出数据正负特性。

3 仿真分析

3.1 仿真环境设置

为了对所提出的方法进行仿真分析验证，利用Matlab构建卷积神经网络和生成神经网络训练数据，整个仿真运行环境如表1所示。

表1 仿真软硬件环境参数

设计服务航天器惯性参数如表2所示，目标航天器的惯性数据如表3所示，组合航天器惯性参数如表4所示。

表2 服务航天器惯性参数

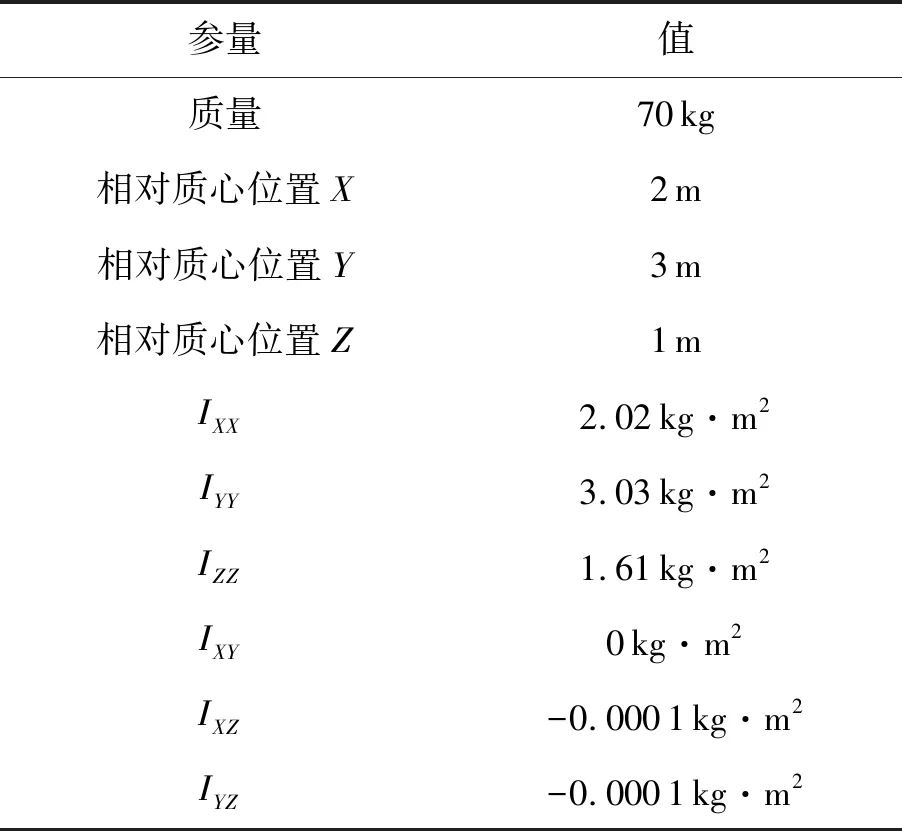
表3 目标航天器惯性参数

表4 组合航天器惯性参数

3.2 质量/质心位置辨识仿真

设组合航天器初始线动量为[-86 147.4 80 284.56 905 891.28] kg·m/s，在航天器三轴方向上施加10-4量级的随机量改变组合体线速度，考虑J2摄动影响，将数据按式(23)分别存入输入输出三维数组中，输入数组大小为6×4×12 500，输出数组大小为3×1×12 500。选择初始学习率为[0.000 5 1 200 1 200 1 200]，每个batch的大小为5，对同一个样本集训练20次。

根据上述条件设置，进行仿真验证，获得结果如图7～图10所示，可见各仿真结果都趋向收敛。经统计如表5所示，从中可以看出最终辨识结果都接近真值。从表5可得质量和X方向的相对辨识相对误差在1%以下，Y和Z轴辨识结果误差相对较大，在3%以下。仿真结果表明运用卷积神经网络可实现对组合航天器质量、质心位置的高精度辨识，且每次样本用时仅1.2 s，整个训练时长仅24 s，实现了快速对质量和质心位置的辨识。

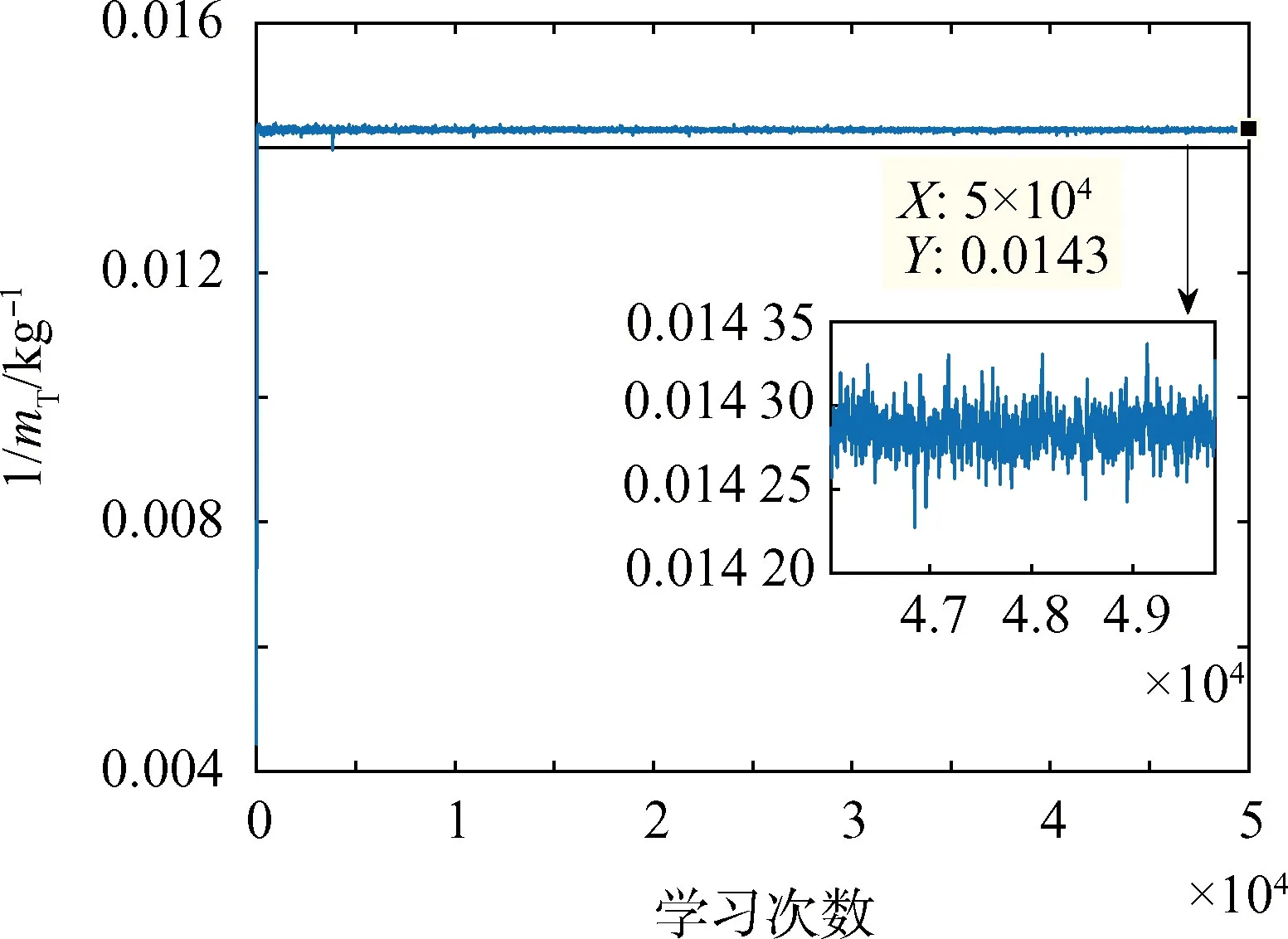
图7 质量辨识结果Fig.7 Result of mass identification

图8 质心位置辨识结果Fig.8 Result of centroid location identification

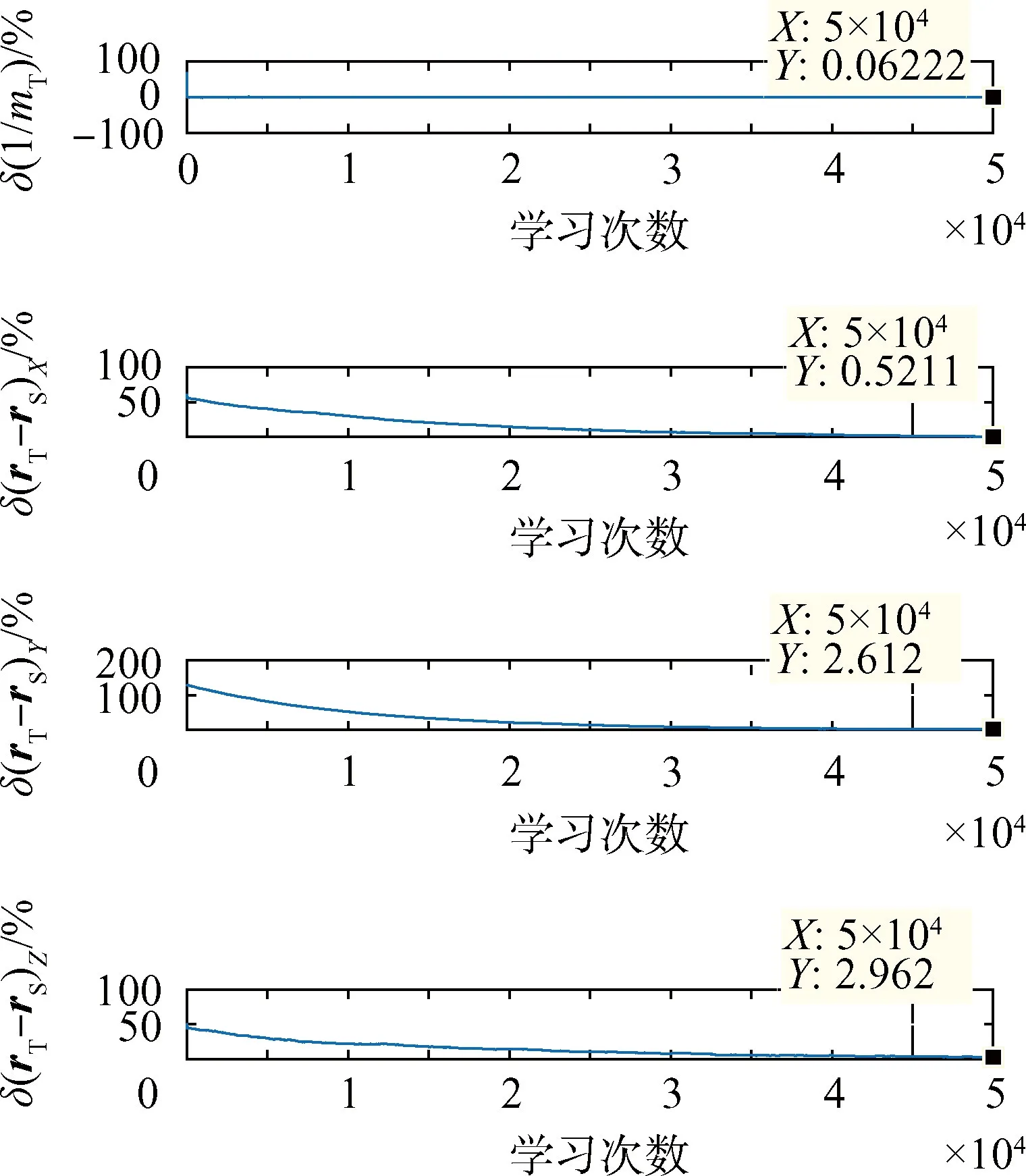
图9 辨识结果相对误差Fig.9 Relative error of identification result

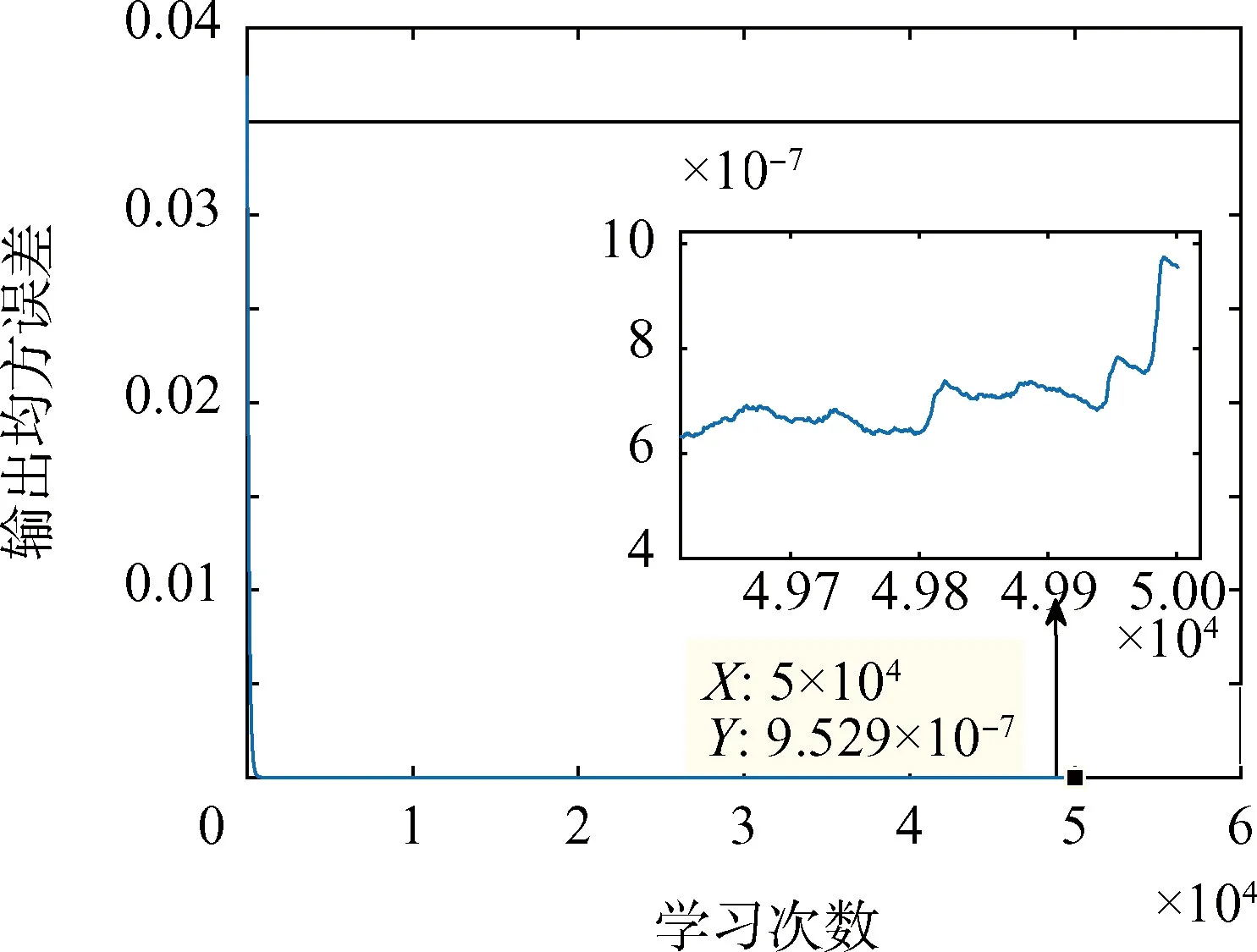
图10 卷积神经网络输出均方误差Fig.10 Mean square error of convolution neural network′s output

参量辨识结果误差/%质量70.028kg0.0622相对质心位置X1.990m0.521相对质心位置Y2.922m2.612相对质心位置Z0.9704m2.962

3.3 惯量辨识仿真

设组合航天器初始角动量为[0.042 24 0.072 36 0.031 32] N·m·s，在航天器三轴方向上施加10-3量级的随机力矩改变组合体角速度，在过程中加入10-6量级的随机外界干扰力矩，按式(26)的格式存储输入输出训练数据，卷积神经网络学习率设置为3，每个批处理的大小为5，对样本集训练700次。

根据上述条件设置，进行仿真验证，获得结果如图11～图15所示，可见各仿真结果都趋向收敛，经统计如表6所示。主转动惯量的误差用相对误差表示，转动惯量积由于是小量，用相对误差不能准确表示精度，采用绝对误差表示。在加入噪声下，主转动惯量的辨识相对误差都在2.6%以下，转动惯量积的辨识绝对误差的量级在10-4，整个训练过程用时1 190 s。仿真表明CNN卷积神经网络可实现对组合体转动惯量的精确辨识。

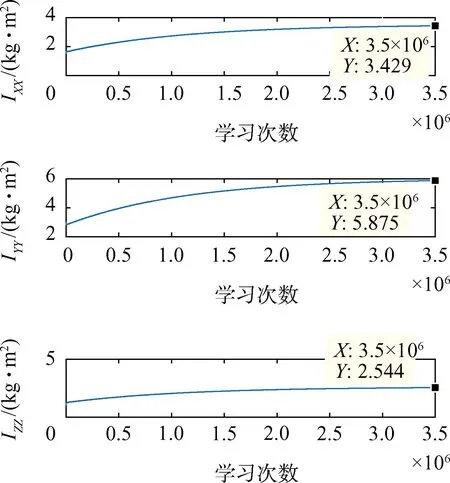
图11 主转动惯量辨识结果Fig.11 Identification result of the principal moment of inertia

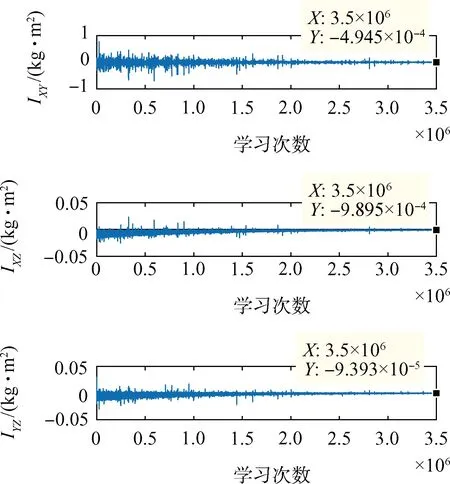
图12 转动惯量积辨识结果Fig.12 Identification result of inertial product

图13 主转动惯量辨识相对误差Fig.13 Relative identification error of the principal moment of inertia

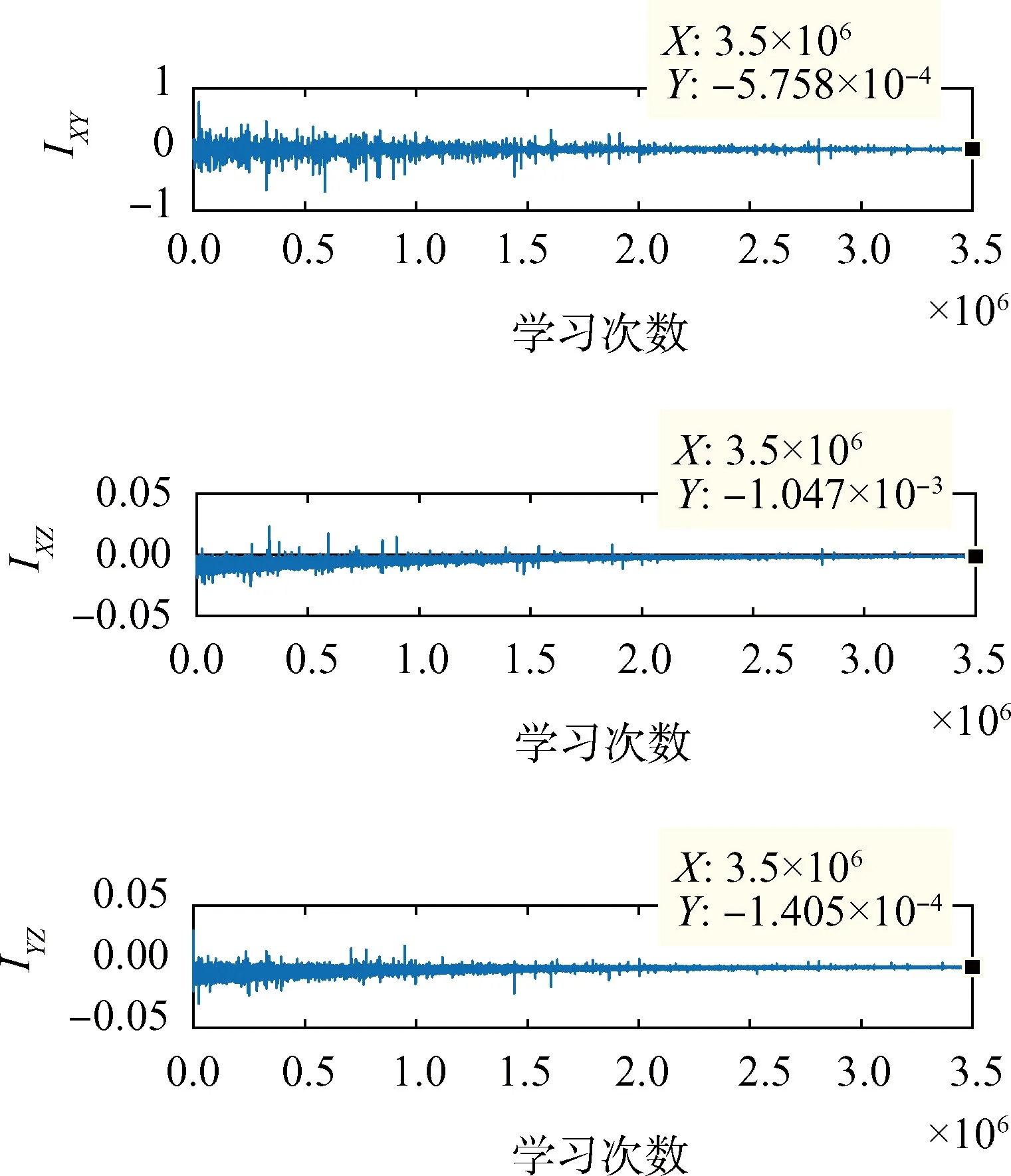
图14 转动惯量积辨识绝对误差Fig.14 Absolute identification error of the inertial product

图15 卷积神经网络输出均方误差Fig.15 Mean square error of convolution neural network′s output

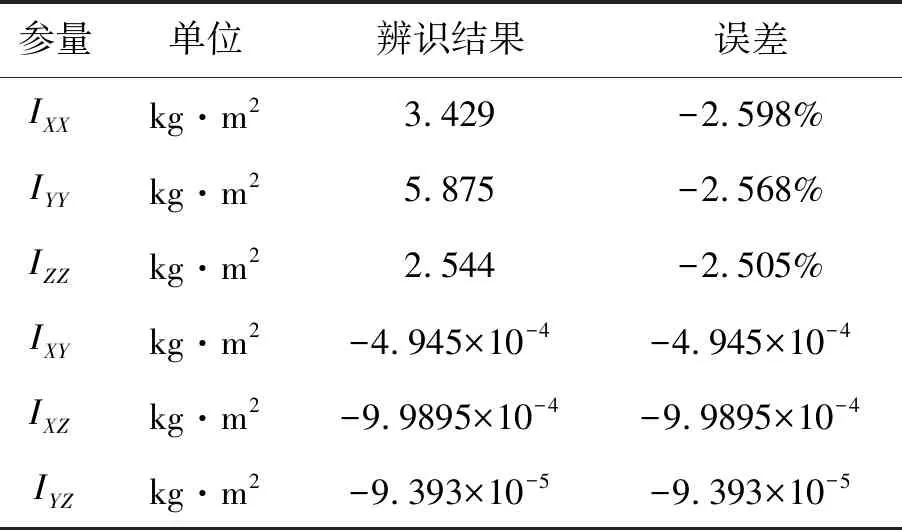
参量单位辨识结果误差IXXkg·m23.429-2.598%IYYkg·m25.875-2.568%IZZkg·m22.544-2.505%IXYkg·m2-4.945×10-4-4.945×10-4IXZkg·m2-9.9895×10-4-9.9895×10-4IYZkg·m2-9.393×10-5-9.393×10-5

4 结束语

本文针对航天器在轨组合参数需重辨识的问题，提出了一种具有普适性的基于CNN神经网络的组合航天器在轨参数辨识方案。仿真分析表明，该方案在24 s内实现对目标航天器质量和质心位置辨识，辨识总体误差控制在3%以内；在1 190 s内实现对目标惯量辨识，误差在2.6%以内。传统最小二乘法只能解决线性回归问题，且计算过程涉及矩阵求逆，计算的时间复杂度大。CNN神经网络方法仅需对组合航天器的状态数据按特定格式进行存储形成训练数据，而不强调数据的实时性，从数据中提取组合航天器质量、质心位置和转动惯量特征值，并且随着训练场景样本的增多，能够累积辨识先验知识，通过先验知识库对CNN神经网络的初值进行选择，能有效降低对样本训练次数以及训练时间要求，达到快速辨识的目的。方法辨识精度高，参数选取自由度大，但对于计算硬件要求相对较高，可以应用于未来组合航天器在轨参数辨识。

未来可通过在地面设置各种航天器组合场景，训练卷积神经网络，训练结果可为在轨实时辨识提供最优初值，加快参数辨识速度。