基于光子集成回路的干涉成像技术

1. 北京空间机电研究所，北京 100094 2. 北京宇航系统工程研究所，北京 100076

传统光学望远镜基于光的折射、反射原理，其光学系统需要复杂的刚性支撑结构[1]，导致光学系统较为笨重；而且超大口径单体镜存在镜坯不易制备、光学加工困难等缺点。近年来，一些新的技术手段被提出以克服这一问题，并使得超轻小型成像系统成为可能。2012年，洛克希德·马丁先进技术中心和加州大学戴维斯分校的研究人员公布了分块式平面侦察成像系统[2-4](Segmented Planar Imaging Detector for Electro-optical Reconnaissance, SPIDER)的新技术，它是基于光子集成回路[5](Photonic Integrated Circuits, PIC)的干涉成像系统。微透镜阵列获取的目标光信息在PIC中进行调相、分波、干涉耦合，并由平衡探测检测输出，获得干涉条纹的可见度和相位，经傅里叶逆变换后获得目标的强度分布。与传统成像系统相比，该技术可以减少遥感载荷的尺寸、质量、功耗(Size, Weight and Power, SWaP)10～100倍，在空间光学遥感、空间态势感知(Spatial Situation Awareness, SSA)等领域应用潜力巨大，是当前研究热点之一。Alan Duncan等[6]人仅给出了SPIDER的结构形式，对平衡检测原理、系统指标未做深入研究。

本文深入研究了基于光子集成回路的干涉成像技术原理、实现方法。建立了基于部分相干光理论的成像模型；分析了平衡正交检测原理；并对基于光子集成回路的干涉成像系统指标进行了分析，最后仿真分析了SPIDER的成像能力。

1 SPIDER成像原理

如图1所示，基于光子集成回路的干涉成像系统由3部分组成：微透镜阵列、光子集成回路和信息处理单元。二维微透镜阵列由多个一维微透镜阵列沿径向排列，一维微透镜阵列中包括多组配对的透镜；PIC芯片集成了光波导阵列(Optical Waveguide Array, OWA)、阵列波导光栅(Arrayed Waveguide Gratings, AWG)、相位调制器、多模干涉(Muti-Mode Interferometer, MMI)耦合器等无源器件[7-9]。多组不同方向、不同长度的基线收集来自目标的光信息并将其耦合到PIC芯片上的波导阵列中，经过阵列波导光栅将光分成多个窄谱段，经过相位调制，使之满足干涉条件。相同的窄谱段光在多模干涉耦合器中耦合并输出到信息处理单元中，由平衡正交检测器(Balanced Four Quadrature Detector, BPD)检测，经过处理得到相干光的相位和振幅信息，通过傅里叶逆变换得到目标的光强分布。

1.1 物面光场分布

从物面到像面，SPIDER成像系统对光信息进行以下光学处理[10]：1)微透镜阵列将光收集到波导阵列中；2)不同的透镜组合成不同方向、长度的基线；3)通过相位延迟、多路复用使光满足干涉条件；4)在多模干涉耦合器中耦合，平衡正交检测干涉条纹获取相应的振幅与相位信息；5)傅里叶逆变换得到物面的光强分布。

光从目标到探测平面实际上是衍射过程。遥感探测中像面与物面之间的距离通常很远，所以像面光强分布I(x,y)物面光强分布I(ξ,η)的关系可用夫琅禾费衍射公式来表示[11]:

(1)

式中：Z为物面到入瞳处距离；k为波数，k=2π/λ。

1.2 干涉条纹检测原理

来自目标的光信息经过阵列波导光栅分成宽度相等的n个窄谱段λ1～λn，经过相位调制使之满足干涉条件，在1×2、2×2的MMI耦合器实现干涉，并由平衡正交探测干涉条纹信息。如图1所示，假设MMI输入的两路光信号为ES和ER(图1中简单表示为S、R)，S和R分别被1×2 MMI耦合器分成两个信号。对于1×NMMI耦合器，输入光信号与输出光信号的相位差为：

(2)

式中：s为输出波导序数(从上往下)；N为输出波导数；φ1s为波导序数为s时输入与输出的光信号的相位差。N=2时 ，φ11=φ12=0 ，1×2 MMI耦合器输出信号与输入信号同相。

而对于N×NMMI耦合器，输入与输出的光信号相位差为：

r+s为偶数：

(3)

r+s为奇数：

(4)

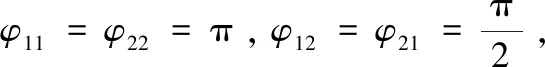
(5)

MMI输入的光信号ES和ER的复数形式为：

(6)

式中：j为虚数单位;AS,AR分别为S、R的振幅;θS,θR为信号初始相位;ωS,ωR为信号频率，经过AWG后MMI耦合器输入为相应的窄谱段，可认为两者频率相同，即ωS=ωR。

ES和ER经过1×2 MMI耦合器无相差输出分别为1/2ES、1/2ES和1/2ER、1/2ER。此时1/2ES和1/2ER在2×2 MMI耦合器中干涉耦合，1/2ES和1/2ER移相90°后在2×2 MMI耦合器中干涉耦合,则上边两路输出为：

(7)

下边两路输出为：

(8)

显然，经过MMI耦合器干涉耦合之后输出的4路电流IQ1(t),IQ2(t),II1(t),II2(t)如下所示(κ为响应度)：

(9)

这样，经过BPD后，得到两路电流值如下式：

(10)

BPD输出的电流与S、R的相差(即光程差(Optical Path Difference, OPD))密切相关。采用MMI耦合器和平衡探测，即可收集光场的强度和相位全部信息[12-13]。

根据范西特-则尼特定理，目标光强分布I(ξ,η)在点(x1,y1)、(x2,y2)的复相干度正比于光源强度分布的归一化傅里叶变换[14]。μx1,x2,y1,y2=

(11)

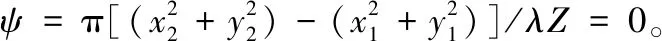
当入射波长一定时，采样获得的目标空间频率与基线矢量有关，一组干涉基线只能得到目标基线方向上的一个空间频率点。通过多个一维微透镜阵列沿径向排列，获得不同方向、不同长度的基线。一次采样获得目标空间频率覆盖，根据式(11),通过傅里叶逆变换获得目标强度分布。

2 成像系统指标

2.1 视场

对于基于光子集成回路的干涉成像系统，单根波导的视场(Field of View, FOV)取决于波导耦合效率。如图2所示，耦合效率为光波导中光功率与光波导端面接收到的光功率的比值[15]。耦合效率随点源到光轴的距离增加而迅速降低。当波导端面为圆形且为基模波导时，耦合效率服从高斯分布[16]：

(12)

式中：f为透镜焦距；d为口径；λ为入射波长；α为点源距光轴的角距；J1是一阶贝塞尔函数；ω是基模的1/e宽度;I0是零阶修正贝塞尔函数；r为无量纲量。对于轴上点fλ/ωd=1.401时，ρ取得最大值，此时有：

(13)

图2 光耦合进光波导示意图Fig.2 Schematic diagram of optical coupling into optical waveguides

显然，耦合效率是|α|的函数，如图3所示，耦合效率随着|α|的增大而迅速减少，轴上点(即|α|=0时)，耦合效率约为81.33%。当|α|=λ/d时，耦合效率下降到8.15%左右，即波导端面上视场边缘的耦合效率约为轴上点耦合效率的10%。这样单个微透镜后单根波导的视场限制为FOVsingle=2×λ/d。

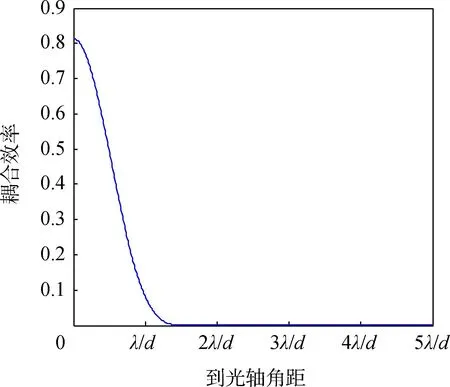
图3 单模波导耦合效率Fig.3 Coupling efficiency of the single-mode waveguide SPIDER

可以看出，单模波导视场较小，通常可以通过增大入射波长或者减少通光口径扩展单模波导视场，但是这两个方法对于视场的提升有限，而且减少通光口径d会急剧减少系统接收的能量，对天基应用不利。

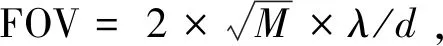
2.2 分辨率

SPIDER成像系统同一干涉臂上每两个透镜组成一条干涉基线，系统在基线方向上的最高分辨率由该方向上最长基线决定。取组成基线的两个透镜，其光瞳[17]可以表示为：

(14)

式中：rect(·)为矩形函数；B为基线长度；d为透镜口径。相应的复振幅分布U2(θ)为：

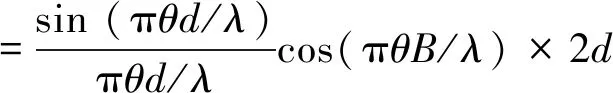
式中：λ为入射波长，对应的光强分为：

=2I1(θ)[1+cos(2πθB/λ)](16)

计算出的光强的第一个零点值对应的θ，就是该方向上的角分辨率θ=λ/2B，这样SPIDER的最高角分辨率为：θmax=λmin/2Bmax，由系统的最长基线Bmax、最短入射波长λmin共同决定[17-18]。

2.3 有效口径

显然，相对于传统的望远镜而言，系统的有效口径就等于系统最长干涉基线Deff=Bmax。

3 SPIDER成像系统仿真

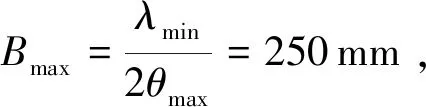
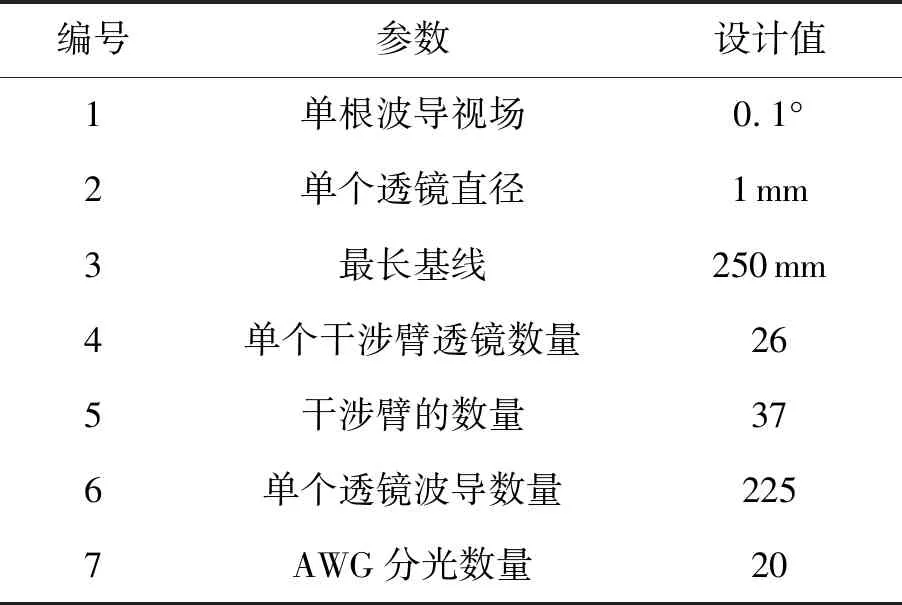
表1 SPIDER成像系统参数设计

每一干涉臂有26个相同大小的微透镜，37个干涉臂组沿径向排列，同一干涉臂上微透镜采用首尾配对方式(即(1,26) (2,25) (3,24) (4,23) (5,22) (6,21) (7,20) (8,19) (9,18) (10,17) (11,16) (12,15) (13,14))组成长度不同的13组基线。相邻透镜等距排列，此时基线长度呈等差分布，分别为250、230、210、190、170、150、130、110、90、70、50、30、10(单位：mm)。对基于光子集成回路的干涉成像技术在500～900 nm谱段范围内成像能力进行仿真验证。

考虑到全视场仿真数据量太大，将系统视场限制在100×100像元靶标大小，验证SPIDER的成像能力。输入靶标如图4(a)所示，SPIDER成像系统UV覆盖如图4(b)所示，经过SPIDER系统重构后的图像如图4(c)所示，图4(d)是输入的原始图像与重构后图像的残差，图像均方根误差(Root Mean Square Error, RMSE)为5.4，成像质量良好。但是从图4(c)中可以看出重构后的图像有一些规律性的条纹出现，这是某些频率信息丢失导致的。

图4 SPIDER仿真结果Fig.4 Simulation result of SPIDER

4 结束语

基于光子集成回路的干涉成像技术突破了单个大口径成像系统口径对分辨率的限制，在深空探测、静止轨道遥感、中低轨道高分辨率成像等方面应用前景广阔。本文研究了SPIDER组成与工作原理，建立了基于部分相干光理论的成像模型；研究了基于平衡正交检测的干涉条纹检测方法；分析了成像系统指标体系；最后对SPIDER成像能力进行了仿真验证。仿真结果验证了SPIDER成像能力，为SPIDER的实际应用奠定了基础。