无源器件无源互调干扰行为建模
2019-05-23
1. 北京理工大学 信息与电子学院,北京 100081 2. 中国空间技术研究院 西安分院 空间微波技术重点实验室,西安 710000 3. 北京经纬恒润科技有限公司,北京 100191
多个载波通过非线性无源器件传输时,输出端会产生无源互调干扰分量,落入接收机通带内时就会形成干扰[1]。一般情况下,输出信号中的各次谐波和偶数阶次的无源互调分量都会落在接收频带外,而奇数阶次的分量可能会落入带内[2]。图1为双载波信号的无源互调干扰频谱示意。另外,无源互调干扰分量的幅值随阶次的增高而减小,所以奇数阶次中的3阶和5阶无源互调分量是形成干扰的主要原因。卫星通信中,由于系统具有高发射功率和极佳的接收灵敏度,这种干扰会更加严重[3-4]。因此,无源互调干扰是卫星通信系统必须考虑的问题之一。
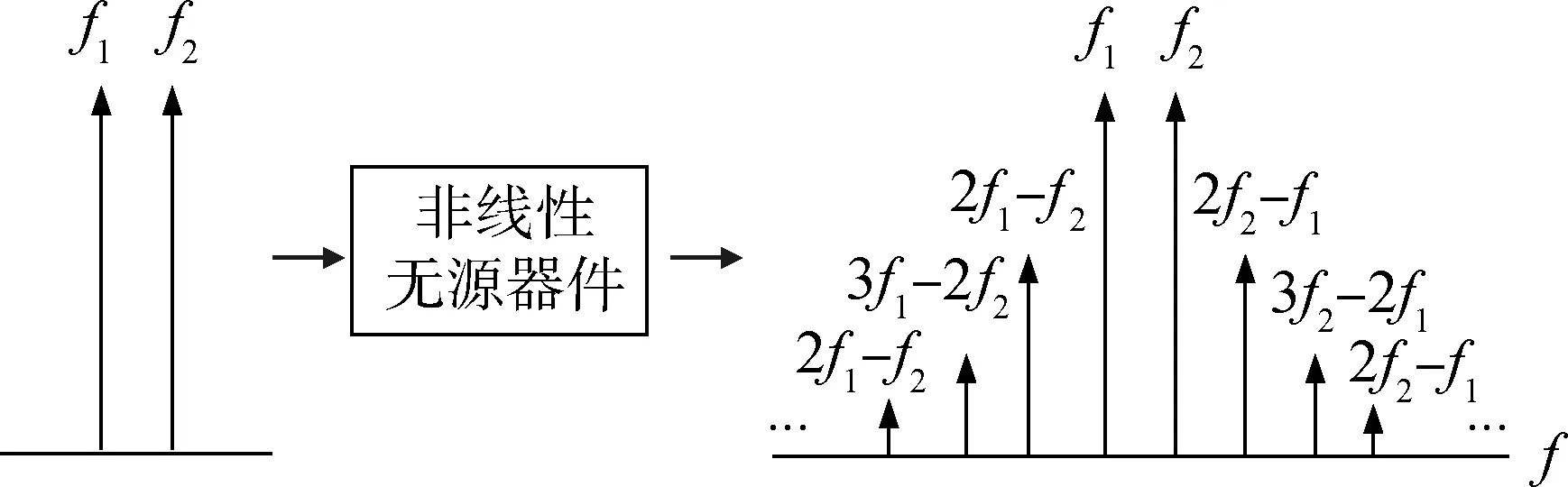
图1 双载波信号的无源互调干扰频谱示意Fig.1 Spectrum of passive intermodulation interference caused by dual carrier signals
目前,已有很多学者对无源互调干扰问题进行了相应研究。Sea[5]提出了利用幂级数模型表征无源器件的非线性特性的方法。Eng和Yue[6]对不同阶数的无源互调分量进行了研究。Heiter[7]介绍了描述非线性器件和系统的简单模型,对幂级数法的功能进行了拓展。Pedro和Carvalho[8]提出了使用双曲正切函数来表征非线性器件的非线性特性。张世全[9]提出使用幂级数模型和傅里叶变换的方法,推导了无源互调干扰信号的表达式。Almudhafar等[10]研究了无源互调干扰信号对通信接收机的影响,并与白噪声存在的情况下进行比较。叶鸣等[11]从测试和频谱算法等方面对无源互调干扰问题进行了综述分析。
由于无源互调干扰问题具有一定的复杂性,直接分析无源互调分量几乎是不可能的,应当建立相应模型进行分析[12]。已有研究中多使用幂级数模型拟合无源互调干扰,但是幂级数模型无法体现非线性行为的记忆性且拟合精度较低,因此需要建立更加合适的行为模型。
1 无源互调干扰模型推导
1.1 基于双指数函数的无源互调干扰模型推导
双指数函数是两个指数函数的组合,可以很好地拟合一些非线性曲线。与幂级数模型相比,双指数函数模型形式相对复杂,但拟合精度较高。幂级数运算复杂度为O(nk) ,而双指数函数的运算复杂度为O(en) ,因此在运算阶数较高时,双指数函数模型具有比幂级数模型更优越的性能。非线性系统的双指数函数表达式为[13]:
(1)
式中:y(t)为系统的输出信号;x(t)为系统的输入信号;V0为非线性拟合系数;b1和b2为线性拟合系数。
这里将双载波信号sdown(t)作为系统的输入信号,
sdown(t)=s1(t)+s2(t)(2)
式中:s1(t)和s2(t)为输入的两个载波信号。
代入双指数函数表达式中,并使用如下索宁扩展式对式(1)进行简化[14]:
(3)
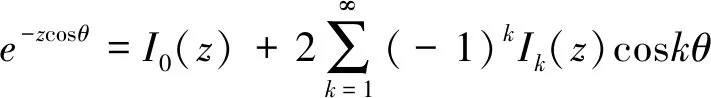
式中:Ik(z)为第一类修正贝塞尔函数中的第k个,则系统的输出信号形式为:
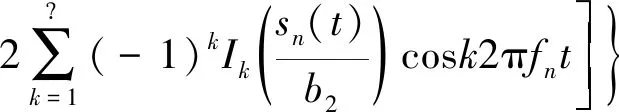
1.2 基于Volterra级数的无源互调干扰模型推导
Volterra级数模型是有记忆性的一般非线性模型。与幂级数模型相比,Volterra级数模型形式较为复杂,但可以很好地体现非线性行为的记忆性。幂级数运算复杂度为O(nk) ,而双指数函数的运算复杂度为O(n) 。因此在运算阶数较高时,Volterra级数模型具有比幂级数模型更优越的性能。Volterra级数模型的具体形式如下[15]:

式中:y(t)为系统的输出信号;x(t)为系统的输入信号;τ为时延。将其扩展为无穷项的形式
y(t)=y1(t)+y2(t)+y3(t)+…+yn(t)+…
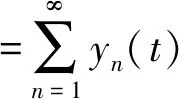
其中:

x(t-τ2)dτ1dτ2(9)
...
x(t-τ2)…x(t-τn)dτ1dτ2…dτn(10)
则y(t)可表示为:
x(t-τ2)…x(t-τn)dτ1dτ2…dτn(11)
式中:hn(τ1,…,τn)为Volterra级数的核函数。Volterra级数模型的原理如图2所示。
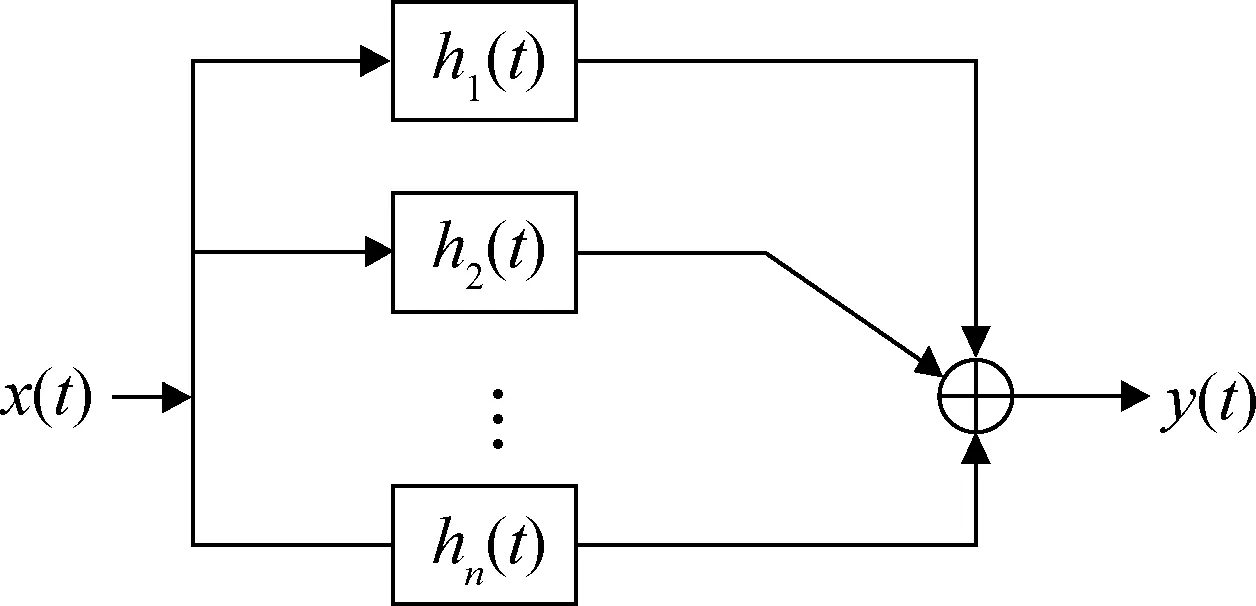
图2 Volterra级数模型原理Fig.2 Schematic diagram of the Volterra series model
2 双载波无源互调干扰信号分析
本文采用QPSK调制的双载波信号作为输入信号进行时域分析。与目前已有研究中多采用的BPSK调制方式相比,QPSK调制具有压缩信号的频带、提高信道的利用率和增加传输效率等特点。
QPSK信号表示为:
sk(t)=Acos(ωct+θk)=Acos(2πfct+θk)(12)
式中:A为载波振幅;ωc为载波角频率;fc为载波频率;θk为载波相位,可以取4个值,
θk=2π(k-1)/M,k=1,2,3,4,M=4(13)
假设系统输入信号sdown(t)由两个QPSK调制的信号s1(t)和s2(t)组成:
sdown(t)=s1(t)+s2(t)(14)
s1(t)和s2(t)的表达式分别为:
s1(t)=hs1·Is1(t)cos[2πf1t+θ1(t)]-
Qs1(t)sin[2πf1t+θ1(t)](15)
s2(t)=hs2·Is2(t)cos[2πf2t+θ2(t)]-
Qs2(t)sin[2πf2t+θ2(t)](16)
式中:hs1和hs2为成形滤波器;两个载波的频率分别为f1和f2;Is1(t)、Qs1(t)、Is2(t)和Qs2(t)分别为两路QPSK调制信号的基带信号;θ1(t)和θ2(t)分别为两路信号载波的相位。
2.1 双指数函数模型的双载波QPSK调制
对式(5)进行化简,将连乘符号进行展开,则系统输出信号可以表达为:
(17)
当k=2时将求和符号进行展开,可得在频率2f1-f2和2f1-f2处的三阶无源互调干扰分量的表达式
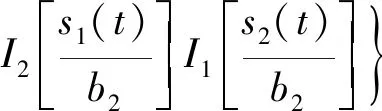
当k=3时将求和符号进行展开,可得在频率3f1-2f2和3f2-2f1处的五阶无源互调干扰分量的表达式

假设非线性系统电压和电流具有奇对称的特性,则设b1=-b2=b=1/a,则3阶无源互调干扰分量的表达式可简化为
yin3(t)=2V0I2[as1(t)]·I1[as2(t)](20)
式中:s1(t)和s2(t)为通过窄带滤波器后的QPSK调制信号;I1(z)和I2(z)分别表示第一类修正贝塞尔(Bessel)函数中的第1个和第2个。
将s1(t)和s2(t)入式(20)中可得
yin3(t)=2V0I2ahs1·Is1(t)cos[2πf1t+
θ1(t)]-Qs1(t)sin[2πf1t+θ1(t)]·
I1ahs2·Is2(t)cos[2πf2t+θ2(t)]-
Qs2(t)sin[2πf2t+θ2(t)]
(21)
对式(21)进行仿真,非线性系统为双指数函数模型,输入信号为QPSK调制的双载波信号,中心频率是f1=22 MHz和f2=24 MHz,码元速率是1.6 Mbit/s。根据理论分析,将在输出信号中产生新的频率分量f=2f1-f2和f=2f2-f1,即3阶无源互调干扰分量。使用MATLAB进行仿真,结果如图3所示。可以观察到在仿真图中,理论值的频点f=22 MHz, 24 MHz, 20 MHz,26 MHz处都有相应峰值出现。通过对仿真值与理论值进行比较,可以得到理论值与仿真值一致,且输入信号中心频率处的幅度值与无源互调频率分量处的幅度值比例近似为9:3,其余频率分量处的无源互调干扰分量落到接收频率之外。
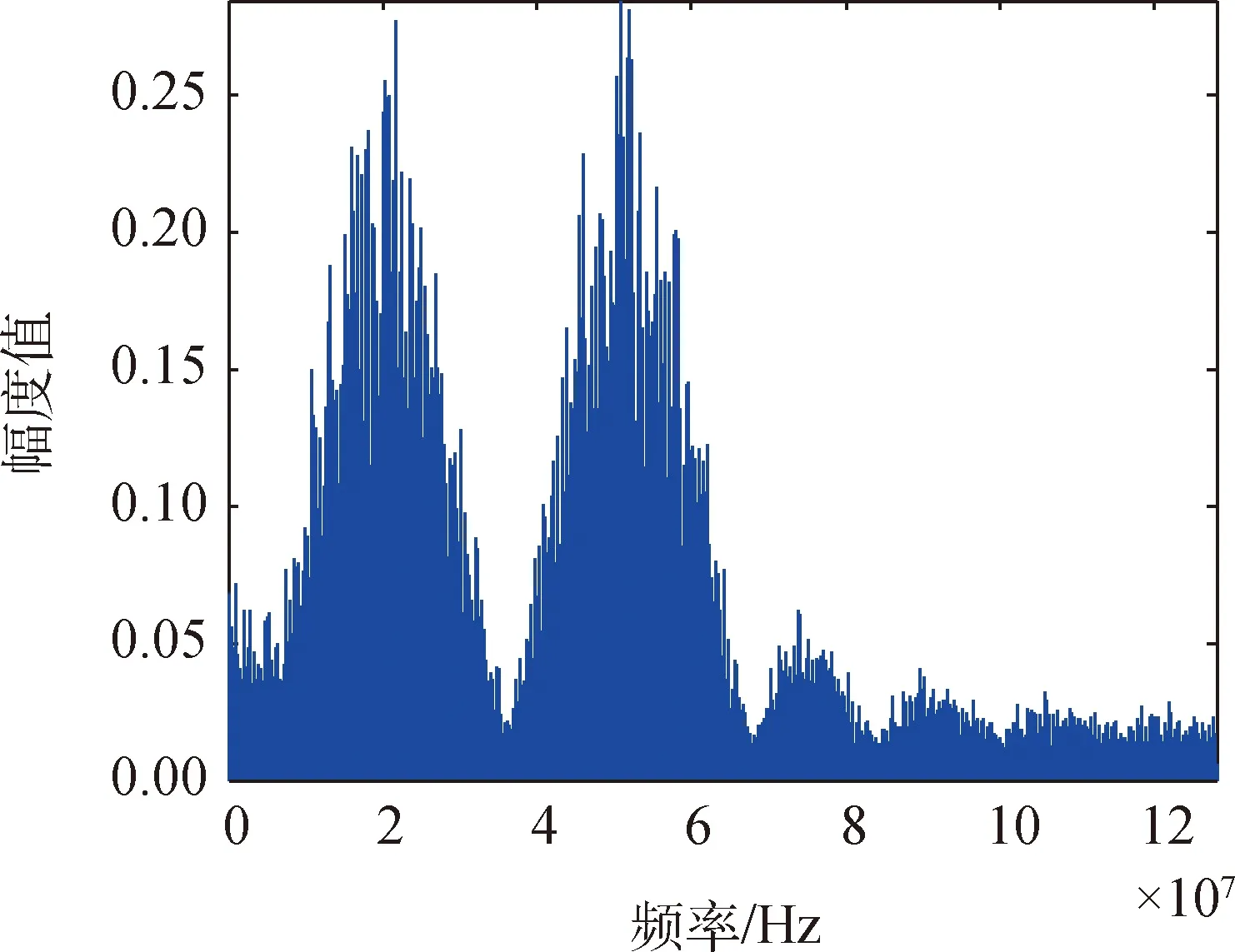
图3 QPSK调制下的双指数函数模型的3阶无源互调分量频谱Fig.3 Third-order passive intermodulation component spectrum of double exponential function model under QPSK modulation
同理可得,5阶无源互调干扰分量的表达式可简化为
yin5(t)=2V0I3[as1(t)]I2[as2(t)] (22)
式中:s1(t)和s2(t)为通过窄带滤波器后的QPSK调制信号;I2(z)和I3(z)分别表示第一类修正贝塞尔函数中的第2个和第3个。
同理,将s2(t)和s3(t)代入式(4),可得
yin5(t)=2V0I3ahs1·Is1(t)cos·
[2πf1t+θ1(t)]-Qs1(t)sin·
[2πf1t+θ1(t)]·I2ahs2·
Is2(t)cos·[2πf2t+θ2(t)]-
Qs2(t)sin[2πf2t+θ2(t)]
(23)
对式(23)进行仿真,根据理论分析,将在输出信号中产生新的频率分量f=3f1-2f2和f=3f2-2f1,即5阶无源互调干扰分量。使用MATLAB进行仿真,结果如图4所示。可以观察到在仿真图中,理论值的频点f=22 MHz,24 MHz, 18 MHz,28 MHz处都有相应峰值出现,通过对仿真值与理论值进行比较,可以得到理论值与仿真值一致,且输入信号中心频率处的幅度值与无源互调频率分量处的幅度值比例近似为25:5,其余频率分量处的无源互调干扰分量会落到接收频率之外。
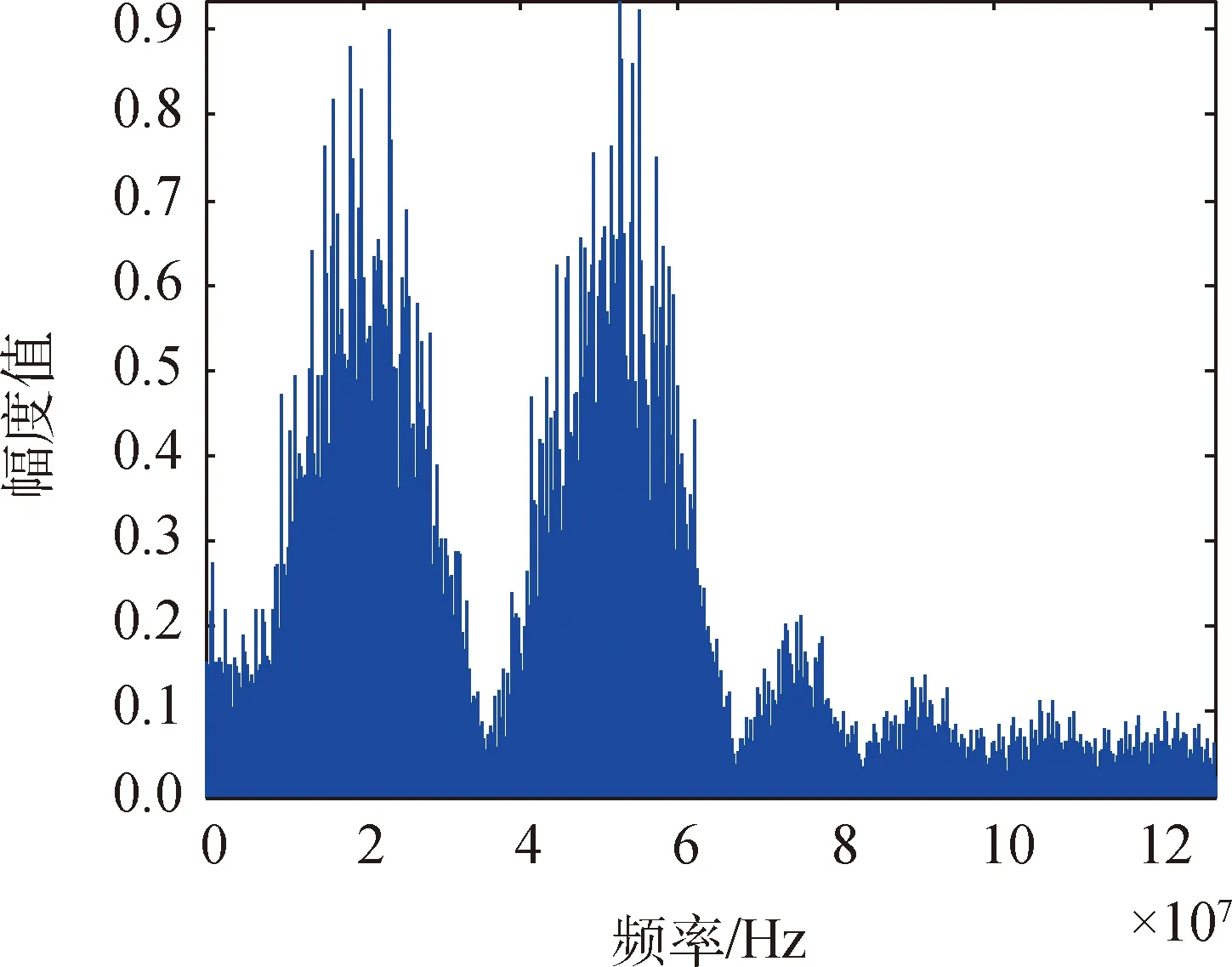
图4 QPSK调制下的双指数函数模型的五阶无源互调分量频谱Fig.4 Fifth-order passive intermodulation component spectrum of double exponential function model under QPSK modulation
2.2 Volterra级数模型的双载波QPSK调制
随着非线性阶数和记忆深度的增加,Volterra级数模型的系数会急剧增加,导致计算复杂度大大增长。记忆多项式模型通过只保留Volterra级数的对角核,在复杂性和模型性能之间实现了很好的折衷[16]。
连续的记忆多项式模型为[17]:
(24)
对于离散时间信号,将式(24)中的积分变为求和,可以表示为[16]:
(25)
式中:x(n)为系统输入信号;y(n)为系统输出信号;K和M分别为记忆多项式模型的阶数和记忆深度;hkm为记忆多项式模型的系数。
根据已有研究[18]中描述的方法,在系统输入信号为双载波QPSK调制信号的背景下,可以得到使用的模型记忆深度M=3时有最好的拟合效果。则输入信号为双载波信号的情况下,3阶无源互调干扰分量表达式为:
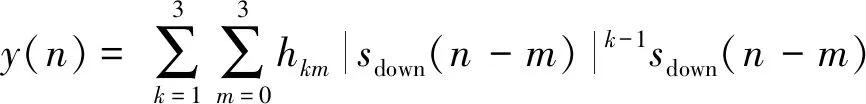
对式(26)进行仿真,非线性系统为记忆多项式模型,输入信号为QPSK调制的双载波信号,中心频率为是f1=22 MHz和f2=24 MHz,码元速率为1.6 Mbit/s。根据理论分析,将在输出信号中产生新的频率分量f=2f1-f2和f=2f2-f1,即无源互调干扰分量。使用MATLAB进行仿真,结果如图5所示。可以观察到在仿真图中,理论值的频点f=22 MHz, 24 MHz, 20 MHz,26 MHz处都有相应峰值出现,通过对仿真值与理论值进行比较,可以得到理论值与仿真值一致,且输入信号中心频率处的幅度值与无源互调频率分量处的幅度值比例近似为9∶3,其余频率分量处的无源互调干扰分量会落到接收频率之外。

图5 QPSK调制下的Volterra级数模型的三阶无源互调分量频谱Fig.5 Third-order passive intermodulation component spectrum of Volterra series model under QPSK modulation
同理可得5阶无源互调干扰分量表达式为:
sdown(n-m) (27)
对式(27)进行仿真,根据理论分析,将在输出信号中产生新的频率分量f=3f1-2f2和f=3f2-2f1,即无源互调干扰分量。使用MATLAB进行仿真,结果如图6所示。可以观察到在仿真图中,理论值的频点f=22 MHz, 24 MHz, 18 MHz,28 MHz处都有相应峰值出现,通过对仿真值与理论值进行比较,可以得到理论值与仿真值一致,且输入信号中心频率处的幅度值与无源互调频率分量处的幅度值比例近似为25:5,其余频率分量处的无源互调干扰分量会落到接收频率之外。
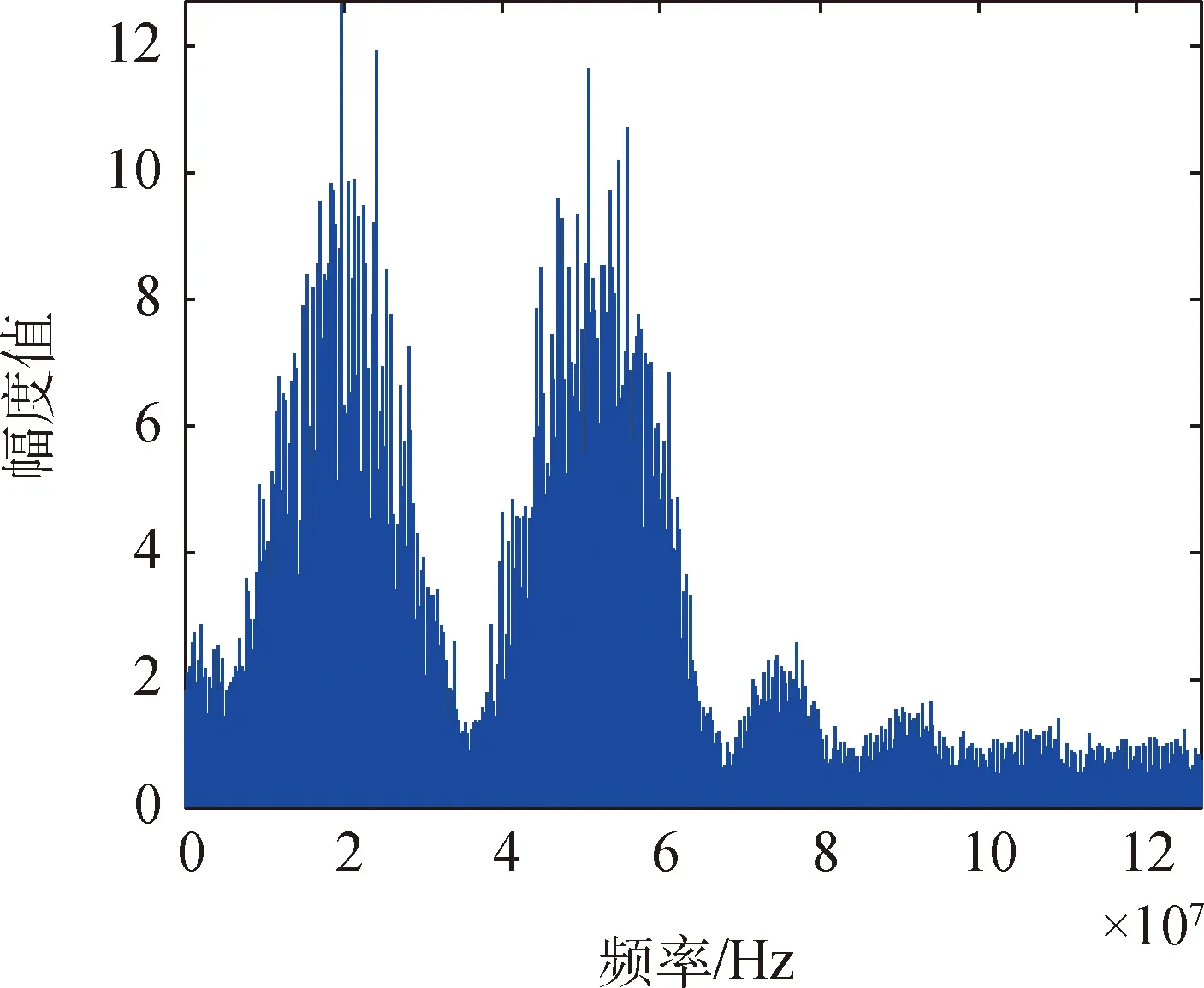
图6 QPSK调制下的Volterra级数模型的五阶无源互调分量频谱Fig.6 Fifth-order passive intermodulation component spectrum of Volterra series model under QPSK modulation
从上述仿真结果可以观察到,峰值出现的频点位置与无源互调干扰分量理论频率相一致:3阶无源互调分量频谱图在f=2f1-f2和f=2f2-f1处都出现了峰值,5阶无源互调分量频谱图在f=3f1-2f2和f=3f2-2f1处都出现了峰值。
3 结束语
本文采用双指数函数模型和Volterra级数模型拟合无源互调干扰,推导了时域表达式并进行了仿真。仿真结果表明,理论值频点处都出现了相应峰值,理论值与仿真值一致,且幅度值与输入信号中心频率处的幅度值的比例符合理论分析。与已有研究中使用的幂级数模型相比,本文建立的模型形式较为复杂,但是运算复杂度较低、拟合精度较高且可以体现非线性行为的记忆性。
本文仅对模型的理论和仿真结果进行了分析和研究,本文得到的结论还需通过实际测量进行进一步的验证。
本文内容丰富了对无源互调干扰行为建模的分析和研究,具有一定的实用性,可以为通信卫星的工程应用提供帮助。
