基于同波束干涉测量的航天器姿态测量研究

2323

1. 北京邮电大学，北京 100876 2. 北京航天飞行控制中心，北京 100094 3. 航天飞行动力学技术重点实验室，北京 100094

卫星姿态描述的是卫星本体坐标系在参考系的指向[1-2]。在轨航天器均有特定任务，在飞行中对飞行姿态及精度均有明确要求。已有文献分析显示，卫星轨道姿态变化对星载合成孔径雷达(SAR)成像效果有较大影响。在一定的成像条件下，卫星三轴姿态变化需满足相应的精度指标，才有可能达到既定的SAR成像精度[3]。通信卫星则需要基于姿态信息将星载天线始终指向地面接收天线。随着中国航天和通信事业的发展，点波束天线以其灵活性好、增益高、安全保密性强等特点，获得了越来越广泛的应用。但是，点波束地面覆盖区域是由点波束天线指向确定的。如果卫星姿态俯仰角发生1°的偏差，点波束中心经度偏移可达十几度，点波束将完全偏离原覆盖区，从而直接导致任务失败[4]。因此，航天器姿态是在轨航天器正常工作的基础性信息。

目前，航天器的姿态确定由姿态敏感器硬件装置和和姿态确定软件算法结合实现[5-7]。常用器件包括激光陀螺仪、星敏感器及太阳敏感器等。航天器姿态敏感器在空间中的指向方位随星体的运行而不断改变, 因此常会受到太阳光的干扰,导致姿态敏感器在受干扰期间无法正常工作[8]。并且无论激光陀螺仪，或是星敏感器、太阳敏感器，均属于星载设备，一旦发生故障则难以维修，甚至造成整星失效。开展地基航天器姿态测量技术研究，则可以避免星载敏感器失灵或者损坏后将无法继续进行航天器姿态测量的风险。

本文利用地基同波束干涉测量技术[9-11]，获取航天器不同位置下行天线到地面测站的高精度距离差测量结果，进而反演解算航天器姿态信息。同波束干涉测量的基本原理是利用天线的主波束同时接收角距很小的两个或多个探测信号，得到两个或多个探测信号的相关相位并进行差分解算。由于探测角距相近，可以消除传播路径以及观测装置的绝大部分影响，得到的差分时延数据比传统的VLBI时延测量精度更高。从测量原理上，同波束VLBI对两个探测信号的相对位置有较强的约束。同波束干涉测量技术已经在深空导航相对测量中得到了充分应用[12-14]。

基于地基同波束干涉测量，首先建立“星载发射天线-地面接收天线”干涉距离差与航天器姿态的函数关系，给出基于干涉距离的航天器姿态方程及解算方法，最后通过数值仿真评估基于地基同波束干涉测量的航天器姿态解算精度。该方法不但适用于大型在轨航天器姿态测量，亦适用于不允许或不能安装传感器、采用地基观测设备开展测量的飞行器姿态测量。

1 基于同波束干涉测量的航天器姿态测量

1.1 同波束干涉测量原理

假设星载天线为n=1,2,…,N，地面天线为m=1,2,…,M。由于星载天线位置变化将带来星载天线与地面天线间距离，即信号传播几何延迟的变化，因此定义星载天线n与地面天线m间几何延迟为τnm；由于同一卫星发射的无线电信号传播至同一测站中，传播介质基本相同，因此定义所有星载天线与地面天线m间电离层延迟、大气延迟、设备延迟分别为τionom、τtropm、τeqm；针对同一地面天线m，定义其接收钟差为τclockm。

假设星载天线n的发射信号为Xn(t)，则经过传播至地面天线m的几何延迟τnm、电离层延迟τionom、大气延迟τtropm、设备延迟τeqm、测站钟差τclockm等，地面天线m接收到的信号为：

Xn(t-τnm-τionom-τtropm-τeqm-τclockm)

星载天线n=1,2至地面天线m=1,2的时延差可以利用干涉测量处理，得到星载天线1到地面天线1，2之间的干涉时延差为：

τ1=(τ12+τiono2+τtrop2+τeq2+τclock2)-

(τ11+τiono1+τtrop1+τeq1+τclock1)(1)

星载天线2到地面天线1，2之间的干涉时延差为：

τ2=(τ22+τiono2+τtrop2+τeq2+τclock2)-

(τ21+τiono1+τtrop1+τeq1+τclock1)(2)

其中利用单星载发射天线下行信号开展干涉测量的原理如图 1所示，利用双星载发射天线下行信号开展同波束干涉测量的原理如图 2所示。因此星载天线n=1,2至地面天线m=1,2的时延差的差分，即同波束干涉时延为：

Δτ=(τ12-τ11)-(τ22-τ21)(3)

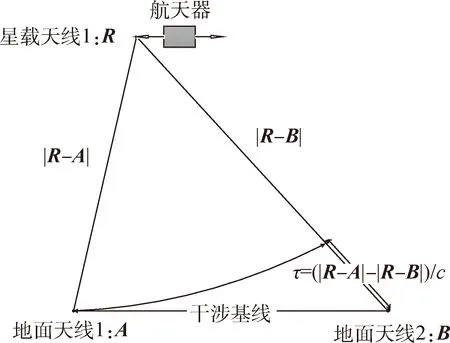
图1 单星载发射天线的干涉测量原理Fig.1 Interferometry with single transmitting antenna

图2 双星载发射天线的同波束干涉测量原理Fig.2 Same-bean interferometry with two transmitting antennas

1.2 基于同波束干涉测量的航天器姿态测量数学模型

不失一般性，基于3个星载天线和3个地面测站开展同波束干涉测量，建立基于干涉时延的航天器姿态解算数学模型。记地固坐标系为直角坐标系O-XYZ。在该坐标系中，已知地面测站坐标分别为A、B、C，航天器坐标为O′。以O′为原点建立航天器轨道直角坐标系O′-X′Y′Z′，其中X′轴指向轨道运行方向，Z′轴指向地心，Y′轴与X、Z′轴成右手直角坐标。以O′为原点建立航天器本体坐标系，其中星载天线位置分别为R′、S′和T′。航天器欧拉角姿态的偏航角、俯仰角、翻滚角均为0时，轨道直角坐标系与本体直角坐标系重合。记航天器欧拉角姿态的偏航角、俯仰角、翻滚角分别为x、y、z。航天器经过偏航角、俯仰角、翻滚角旋转后，星载天线在地固坐标系中的坐标为R、S、T。利用同波束干涉测量，得到R、S到达A、B的距离差a，R、T到达A、B的距离差b，R、S到达A、C的距离差c，由此解算R′、S′、T′旋转至R、S、T的偏航角x、俯仰角y、翻滚角z。

根据该原理，建立数学模型为：

(4)

式中：

R=Ro×Rx×Ry×Rz×R′+O′

S=Ro×Rx×Ry×Rz×S′+O′

T=Ro×Rx×Ry×Rz×T′+O′

其中：Ro为轨道直角坐标系至地固直角坐标系的旋转矩阵，由航天器运行坐标与速度唯一确定；Rx、Ry、Rz分别为由偏航角、俯仰角、翻滚角带来的本体直角坐标系至轨道直角坐标系的旋转矩阵，

1.3 基于干涉时延的航天器姿态解算

根据上述分析，利用同波束干涉测量结果解算航天器姿态信息的等效为式(4)模型的解算。对于非线性方程(4)，本节给出牛顿迭代法解算方法[15-16]。

首先利用泰勒级数对式(4)在旋转角θ=[x,y,z]T处进行展开。为表示方便，令f(θ)=f(x,y,z)=[f1(x,y,z),f2(x,y,z),f3(x,y,z)]T，其中:

f1(x,y,z)=(|R-A|-|R-B|)-

(|S-A|-|S-B|) (5)

f2(x,y,z)=(|R-A|-|R-B|)-

(|T-A|-|T-B|) (6)

f3(x,y,z)=(|R-A|-|R-C|)-

(|S-A|-|S-C|) (7)

给定旋转角初始估计θ0=[x0,y0,z0]T，将f(θ)在初始值θ0处进行一阶泰勒级数展开可得

f(θ)=f(θ0)+J(θ-θ0)+O(‖θ-θ0‖)(8)

f(θ0)+J(θ-θ0)为f(θ)的一阶近似，为雅克比矩阵J，O(‖θ-θ0‖)表示高阶项，其中

忽略高阶项，可以根据距离差方程组得一阶近似方程

f(θ)=f(θ0)+J(θ-θ0)=d(9)

经整理可得

J(θ-θ0)=d-f(θ0)(10)

对方程(10)两边同时左乘矩阵J的转置可得

JTJ(θ-θ0)=JT[d-f(θ0)](11)

由方程(11)可得

(12)

其中旋转角初始估计θ0=[x0,y0,z0]T及f(θ0)、距离差矢量d=[a,b,c]T已知。问题的关键是如何解算出雅克比矩阵J，详细推导过程如下：

由定义可知距离项|R-A|，|R-B|，|R-C|，|S-A|，|S-B|，|S-C|，|T-A|，|T-B|是关于旋转角θ=x,y,zT的复合函数，需要利用链式求导法则对这些项进行求导。令ρA,B=(A-B)/|A-B|，Ψ=RxRyRz，可得

其中:

由此可得

(13)

其中:

RAB=(ρR,A-ρR,B)T[ΨxR′,ΨyR′,ΨzR′]

SAB=(ρS,A-ρS,B)T[ΨxS′,ΨyS′,ΨzS′]

TAB=(ρT,A-ρT,B)T[ΨxT′,ΨyT′,ΨzT′]

RAC=(ρR,A-ρR,C)T[ΨxR′,ΨyR′,ΨzR′]

SAC=(ρS,A-ρS,C)T[ΨxS′,ΨyS′,ΨzS′]

至此，解算得到雅克比矩阵J。

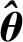
1.4 方程可解性分析

理论上，方程可解的充分条件是矩阵JTJ可逆(满秩)，而JTJ满秩的条件是雅克比矩阵J必须满秩。受地面测站和航天器下行天线相对位置影响，雅克比矩阵J存在不满秩的可能，将导致解算过程中出现迭代发散。同时，如果雅克比矩阵J条件数较大时，亦存在解算过程中精度因子过大的情况。

通过分析可知，雅克比矩阵J满秩须满足航天器上R，S，T中任意两点与测站A，B，C中任意两点不能共线等条件；而雅克比矩阵J条件数理论分析则较为复杂，工程实现中可以通过设定精度因子门限选择应用。

1.5 解算精度因子

在姿态方程可解条件下，由式(12)可知航天器姿态解算误差协方差矩阵为(JTJ)-1，令

则航天器姿态解算精度(即精度因子)可以定义为

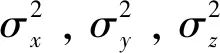
1.6 解算精度与最小观测俯仰角关系理论分析

以星载天线R，S到达地面天线A，B的距离差d为例，航天器姿态变化引起的距离差d的变化值为Δd。在观测俯仰角较大时，距离差d很小，变化值Δd相对于距离差d的比值Δd/d较大，因此在解算过程中能够以较高的精度得到航天器姿态的变化，即所获得航天器姿态解算误差较小；相反，在观测俯仰角较小时，由于距离差d很大，所获得航天器姿态误差较大。实际测量中，在不同的观测俯仰角由姿态变化引起的距离差变化值Δd存在差异，但是这种差异引起的姿态变化误差相对于距离差d引起的误差可以忽略不计。

2 地基航天器姿态测量数值仿真

首先模拟在轨航天器的轨道仿真，开展同波束干涉测量仿真实验；然后由基于干涉时延的航天器姿态测量数学模型和航天器姿态解算方法，迭代解算航天器姿态信息。

不失一般性，假设航天器轨道高度为400 km，轨道倾角为40°，偏心率为0°；航天器理论姿态(欧拉角)为偏航角5°、俯仰角-3°、翻滚角2°。星载天线在航天器本体直角坐标系中的坐标为R′=[50,0,0]，S′=[0,50,0]，T′=[0,-50,0]。

地面主站坐标为：东经110°、北纬25°、高程0 m，基线长度1000 km。根据航天器轨道和主站坐标位置信息，得到航天器运行星下点及主站位置示意如图3所示。

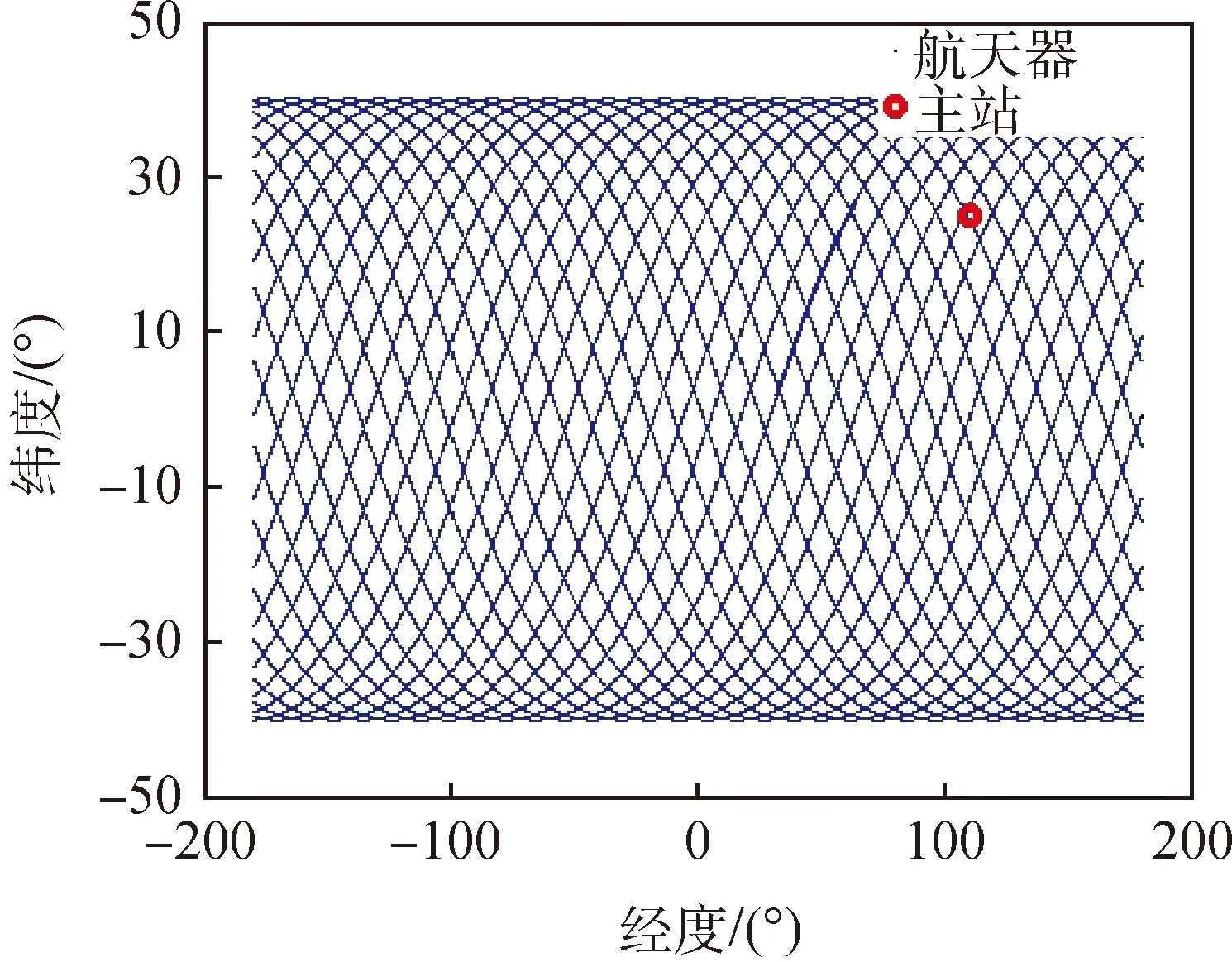
图3 航天器运行星下点及主站位置示意Fig.3 Diagram of star points in spacecraft operation and main station coordinates

利用航天器轨道信息，得到星载天线至地面天线距离差模拟值，模拟值由理论值叠加测量噪声得到，其中同波束干涉频率设定为S波段，相位测量噪声取方差为1/50周的高斯白噪声。

航天器姿态信息解算时，设定航天器偏航角、俯仰角、翻滚角初值均为0°，进行航天器姿态迭代解算。迭代次数超过10或迭代改进量小于0.01°时迭代强制结束。由于雅克比矩阵不满秩情况的存在，在解算过程中会出现迭代发散、不断进行迭代和精度因子过大的情况，需要对其进行判断。

2.1 迭代收敛判断

设定最小观测俯仰角为5°、测量时间间隔为1 s，则在2天时间内，地面测站对航天器的观测时长约2 850 s。该观测时间中，航天器姿态解算误差与迭代次数仿真结果如图 4所示。由于雅克比矩阵存在不满秩或条件数较大的情况，因此解算过程中可能迭代发散(由于本仿真迭代次数超过10将强制结束，因此迭代次数超过10时可以理解为迭代发散)或迭代次数较多。根据图 4可以知道，剔除迭代次数超过10(迭代发散)的结果，亦存在部分较大的解算误差。这是因为雅可比矩阵条件数较大导致。因此需进一步考虑精度因子约束，进一步提高解算结果的有效性。

图4 迭代次数与解算误差仿真结果Fig.4 Simulation results of calculation error and iteration numbers

2.2 精度因子与航天器姿态解算误差关系

剔除迭代次数超过10的解算结果，设定不同精度因子限制，分别得到航天器姿态解算误差与精度因子的关系。譬如，设置精度因子小于0.4(如图 5所示)，航天器姿态部分解算结果仍存在较大误差，其原因是雅可比矩阵条件数较大导致解算结果偏差较大。

经试验测试，当精度因子小于0.19时，解算误差小于0.04°(如图 6所示)。而且此时解算误差与精度因子基本成正比关系。因此可将0.19作为精度因子与解算误差关系的一个临界经验值。

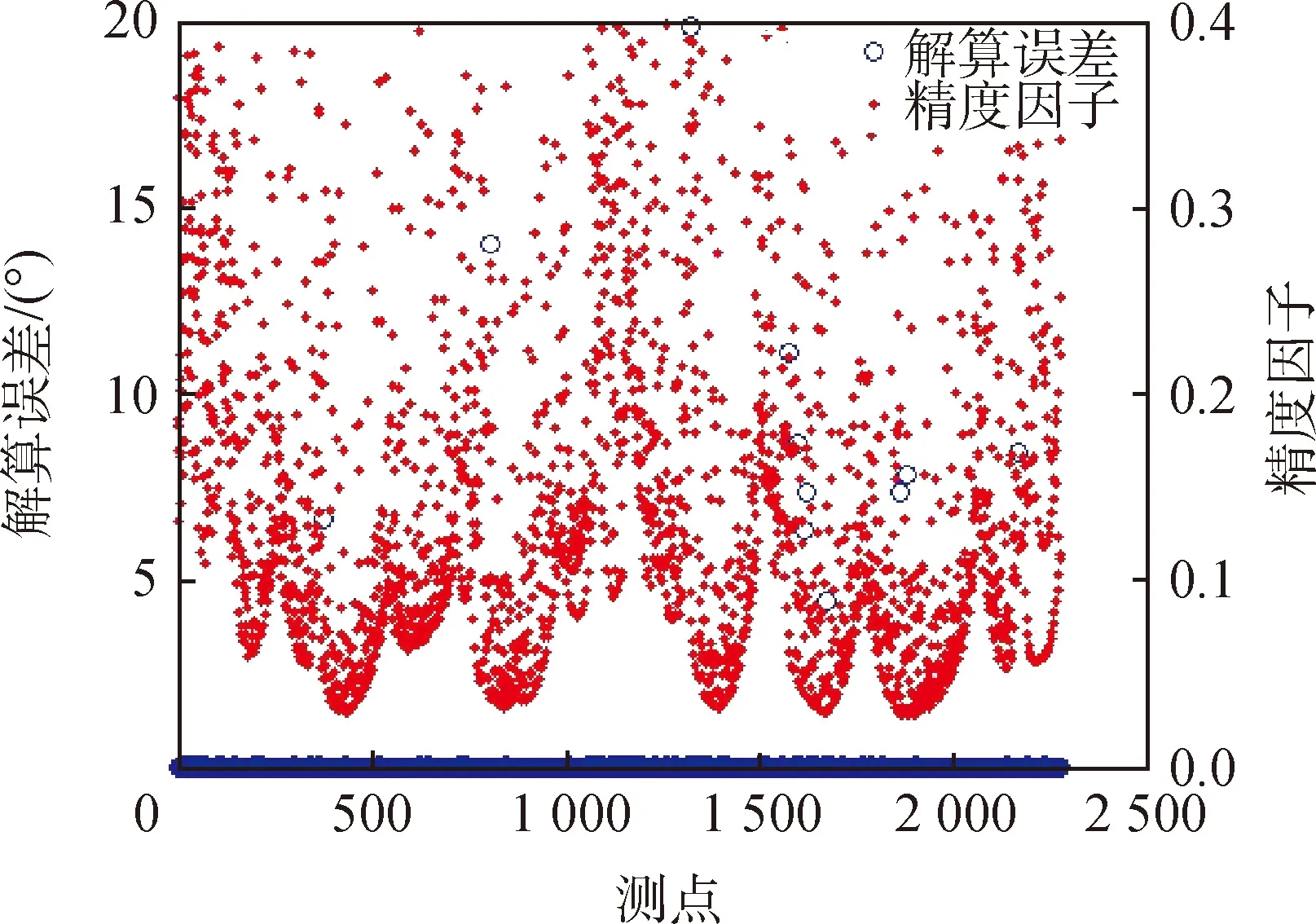
图5 精度因子σ与解算误差仿真结果(σ<0.4)Fig.5 Simulation results of calculation error and precision factor (σ<0.4)

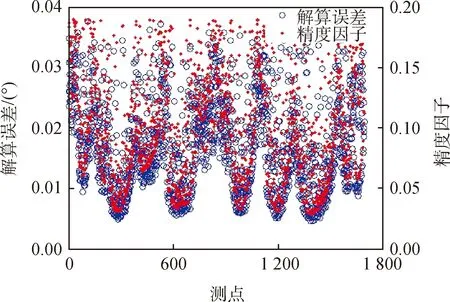
图6 精度因子σ与解算误差仿真结果(σ<0.19)Fig.6 Simulation results of calculation error and precision factor (σ<0.19)

2.3 最小观测俯仰角与航天器姿态解算误差关系

选择迭代次数不超过10且精度因子小于0.19的解算结果，得到航天器姿态解算误差与最小观测俯仰角(即3个测站观测航天器俯仰角的最小值)的关系如图 7所示。

可以看出，航天器姿态解算误差和最小观测俯仰角基本呈反比关系，即3个测站观测航天器的最小俯仰角越大，航天器姿态(欧拉角)误差越小。

2.4 测量误差精度

经仿真试验测试，当干涉频率为S频段(约2.2 GHz)、干涉相位提取精度为1/100周时，航天器姿态解算精度可以达到0.001°量级；干涉相位提取精度为1/50周时，航天器姿态解算精度可以达到0.01°量级。

3 结束语

针对航天器姿态的地基测量需求，本文建立了基于同波束干涉时延的航天器姿态测量数学模型。针对该数学模型，推导了航天器姿态解算方法，给出了解算精度因子，初步分析了该模型的可解性。通过模拟在轨航天器轨道运行过程，针对航天器姿态测量进行了数值仿真试验和误差分析。结果显示，利用3个地基测站针对常见空间站轨道运行的航天器3个下行天线进行同波束干涉测量，辅助精度因子约束，可以有效解算该航天器姿态信息。而且3个测站观测航天器的最小俯仰角越大，航天器姿态解算误差越小。作为地基测量，本文方法可以作为现有星基测量方法的备份。

需要说明的是，基于同波束干涉时延的航天器姿态测量数学模型中由于雅克比矩阵不满秩导致解算迭代发散的理论分析还有待进一步开展。此外，本文在航天器姿态解算中采用了精度因子约束的经验值，亦需要后续理论分析论证。