以史为鉴透析初中数学课堂案例两则

☉重庆市万州江南中学 李吉海

☉重庆市万州第二高级中学 向 鑫

☉重庆市万州第二高级中学 谭忠合

一、为什么要在初中数学教学中融入数学史

学校教育是人类社会文明发展到一定程度后能够快速使少年儿童掌握人类文明精华的有效手段，也是弘扬中华传统文化的必需.然而，在现代课堂上，特别是初中数学课堂上，教师和学生更多的是关注知识、方法和技能本身的训练和掌握，是一种“掐头去尾烧中段”的投机方式，学生往往不清楚某些数学知识的来龙去脉，也就不能真正理解并享受数学之美.古人云：“以史为鉴，可以知兴替”，在日常教学中巧妙渗透数学史，能达到数学激趣、提升数学文化素养、促进学生全面发展的目的.

数学学科的产生源自于人类的生产和生活，经过人们不断的归纳总结慢慢地形成了一个又一个数学模型，因此人类社会发展推动了数学的发展，一代代数学家对数学问题的研究又反过来推动了人类的进步.美国著名的数学史家卡约黎指出，一门学科的历史知识能够激发学生的学习兴趣，使他们树立正确的价值观.因此，数学史对于数学教学来说就是一种十分有效、必不可少的工具.让学生体会到“数学好玩，玩好数学，玩数学好”.

下面以笔者所在地区使用的华东师范大学出版社出版的初中数学教材两则课堂教学案例为例，来探讨运用数学史提升学生认知能力、培养数学建模能力的课堂案例，以期抛砖引玉.

二、数学史融入初中教学的两则案例

案例1：七年级上册“有理数”概念的辨析.

现在的初中数学教材，对于有理数和实数的定义，采用的并不是常见的“属+种差”式定义，而是用的分类法，整数和分数统称有理数，有理数和无理数统称实数.在教学中，按照一般的讲授模式，教师只要再强调有限小数和无限循环小数可以化为分数后，学生就能很快判断一个数是否为有理数，再将π等常见特殊非有理数加以强调，就能达到一个很好的教学效果.但是，学生就会有疑问：“为什么叫有理数”？

“有理数”这一名称不免叫人费解，有理数并不比别的数更“有道理”.事实上，这是一个翻译上的失误.有理数一词是从西方传来，在英语中是rationalnumber，而rational通常的意义是“理性的”.中国在近代翻译西方科学著作时，依据日语中的翻译方法，以讹传讹，把它译成了“有理数”.但是，这个词来源于古希腊语λογο，其英文词根为ratio，就是比率的意思（这里的词根是英语中的，希腊语意义与之相同），原意为“成比例的数”（rationalnumber），是一个整数a和一个非零整数b的比（ratio），通常写作，故又称作分数.所以这个词的意义也很明显，就是整数的“比”.与之相对，“无理数”就是不能精确表示为两个整数之比的数，而并非没有道理.

也就是说，我们要判断一个数是有理数还是无理数，正确的做法不是把它化为小数，看它到底是“有限小数”“无限循环小数”还是“无限不循环小数”，而是要倒过来，看看它能不能化作“可比数”即分数.任何“无限循环小数”都是可以化为分数的，例如：用解方程法把循环小数0.3化成分数，如下：

即9x=3.

案例2：八年级上册“两数和乘以这两数的差”.

上一案例侧重于概念实质的辨析，本案例侧重于通过数学史的渗透达到激发学生学习兴趣、培养学生数学思维能力的效果.

“两数和乘以这两个数的差”简称平方差公式，是八年级上册整式乘法中的一节，实际上学生运用多项式乘以多项式的法则完全可以推出并掌握这一知识.但是，按照传统的知识讲解与训练难以提升课堂的质量和高度，因此本节课的设计笔者采用如下流程：

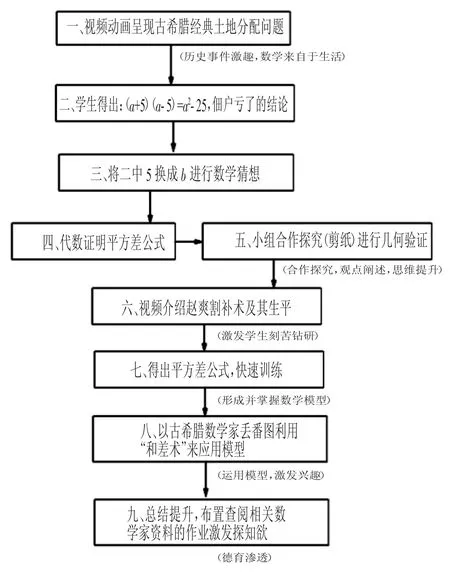
本案例利用数学史经典问题为主线，对相关数学家的生平和解决问题的思维方式进行介绍，整节课教学效果良好，有效地提高了课堂质量，有利于学生数学素养的形成.

三、数学史料的选取与运用策略

对数学史料的选取可以采用以下原则：

1.正确性原则

数学是一门严谨的学科，对历史资料的选取必须查证正确无误后才能向学生讲授.

2.契合性原则

在一节课中通过数学史的运用来提升课堂质量，史料的选用必须符合本节课要讲授的内容，不能为了用数学史而用数学史.

3.整合性原则

在案例2中可以涉及很多数学家，但是通过设计和选择，将古希腊经典土地分配问题作为引入材料，并通过赵爽割补术来验证平方差公式，又用丢番图“和差术”来运用平方差公式，有效地整合了数学史料，从而有效地完成了教学目标.

4.激趣原则

选用数学史在教学中使用，可以通过经典数学历史问题及数学家的故事来激发学生的数学学习热情，渗透德育目标.

5.可接受原则

选用的历史资料，要易于学生理解和接受.

建议教师加强数学史学习，在教学过程中，根据实际教学需要，采用讲授故事法、文献查阅法及数学思想渗透法等方法渗透数学史.通过数学史达到透析数学知识、让学生知其然并知其所以然的目的.