非线性动力学系统的精细逐块积分求解方法*

2019-05-22陈军委

飞控与探测 2019年2期

陈军委

(1. 上海航天控制技术研究所·上海·201109；2.上海市空间智能控制技术重点实验室·上海·201109)

0 引言

对实际动力学系统特性的分析要求有效的数值仿真求解算法，尤其要求在采用大步长时仍然具有高精度的算法[1]。对于不存在或可以忽略高频的结构动力学问题，普遍使用隐式积分方法(如Newmark、Wilson θ和Houbolt方法等)[2]或显式方法(如Runge-Kutta法)进行瞬态分析和求解。通常，这些方法对于线性系统是准确和稳定的。例如，Newmark积分对于线性问题具有二阶精度，并且无条件稳定。然而，当将上述方法应用于非线性动力学系统时，为获得精确和稳定的数值解，选取的步长与系统最小周期、外部激励周期和系统非线性项的变化周期相比，必须足够小。因此，这些方法对于非线性动力学系统的求解效率不高，甚至容易失效[3]。

为此，研究者开发了面向非线性动力学系统的众多数值方法，比如引入数值阻尼[4]，通过Lagrange乘子强制能量守恒[5]，以及采用算术能量守恒[6-7]等方法。Bathe等人提出了一种复合隐式积分算法，用于处理非线性问题[8-9]和线性刚性问题[10]。与上述富有成效的工作不同，本文作者采用了基于积分方程的方法。通常，积分格式会更具优势。理论上讲，积分算子比微分算子更容易实现处理，采用积分格式能更轻易推断出解的特性。事实上，积分格式还可以在某些情形下缩减对象的维度[11]。

具体地，采用精细积分方法(precise integration method，PIM)[12]，指数矩阵的计算可以达到计算机的精度。Zhong、Williams和Lin等人指出，基于不可分割步长，精细积分可以获得无条件的稳定性[12-14]。而Wang等人认为，虽然在考虑子步长的高阶项截断时，精细积分是条件稳定的，但大多数离散模型可以轻易满足这种稳定条件[15]。此外，一阶对角Pade近似对于精细积分也是无条件稳定的[16]，因此，精细积分由于具备高精度和稳定性，可被应用于处理非线性动力学问题。

在执行精细积分时，不可避免地需要计算关于非线性项和外部激励的Duhamel积分。Zhong[13]和Lin等人[14]给出了外部激励为线性、多项式、正弦和指数方程等形式或其组合形式时的积分精确计算公式。然而，这些计算公式并不适用于系统系数矩阵奇异或接近奇异的情况。Gu等人[17]基于多维展开的方法提出了一种修正的精细积分方法，来避免矩阵求逆。由此，原有的非齐次方程将转化为齐次方程，但同时计算量也极大地增加了。Wang等人[15]通过显式Gauss求积处理了Duhamel积分，但其准确性极大程度地依赖于Gauss求积的点数。Li等人[18]在每一个步长内使用了Lagrange三次插值近似非线性项，但仍然需要执行指数矩阵的求逆操作。

本文基于精细积分方法，针对非线性动力学系统，提出了精细逐块积分方法(precise block-by-block integration method，PBIM)。此方法高度精确，在使用大步长时也可保持稳定，无须矩阵求逆便可以处理非线性项。本文余下内容依次为：在第二部分，描述了精细逐块积分方法，以及其精度和稳定性分析；在第三部分，列举了三个数值算例以验证本方法的有效性；最后，在第四部分给出了有关结论。

1 精细逐块积分方法

1.1 方法描述

具有时变刚度的二阶动力系统通常以矩阵形式表示为

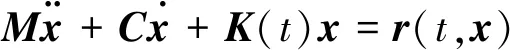
(1)

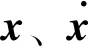
不失一般性，K(t)可以划分为定常部分和时变部分，即K(t)=K1+K2(t)。式(1)由此可以变换为如下的一阶形式

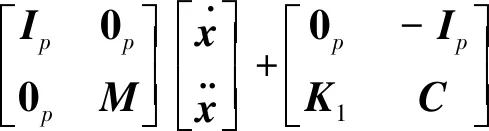
(2)

其中，Ip和0p分别是p×p阶单位阵和零矩阵。

式(2)可以改写为

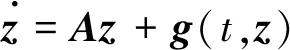
(3)

其中，

令n=2p。显然，A是n×n阶常矩阵，g(t,z)是关于时间、状态向量和外部激励的n维向量方程。需要指出的是，式(3)是相比于式(1)更为通用的形式，虽然前者由后者推导而来。下文将以式(3)为对象进行讨论。

将式(3)进行积分，得到第二类非线性Volterra积分方程，即

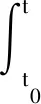
(4)

由于式(3)源于实际动力系统，所以认为其积分核满足Lipschitz条件，即系统存在唯一解[11]。以步长h为离散时间间隔，记离散时间点的状态为zi(i=0,1,2,…)，即zi=z(ti)。定义时间间隔[t2m,t2m+2](m=0,1,2,…)为一间隔块，则在每一间隔块内，得

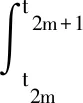
(5)

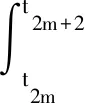
(6)

对式(5)～(6)应用Simpson法则，得

(7)

(8)

由此，Duhamel积分可由精细积分求取[12]。在整个计算流程中，指数矩阵只需被计算一次。以eAh为例，应用指数函数的附加定理，即2N算法，得

eAh=T2N

(9)

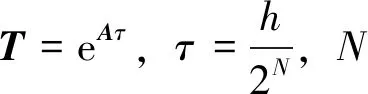
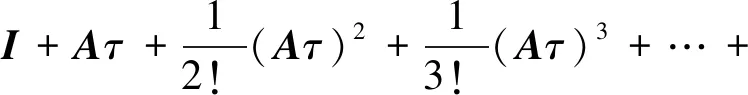
(10)

其中

(11)

τ非常小，故将前4项或前5项展开，便可获得足够高的精度。为避免出现运算圆整误差，可将不变部分I和增量部分Ta分别进行存储。将eAh进行分解，代入式(10)，可得

T2N>=>(T2)2N-1=(I+2Ta+Ta·Ta)2N-1

(12)

最终，经N次形如Ta⟸2Ta+Ta·Ta的递归，eAh的数值结果逼近了计算机的运算精度。

需要指出的是，式(7)～(8)要同时求解未知量z2m+1和z2m+2。在此，可以应用任何代数方程求解算法。例如，可以使用Newton迭代下山法以避免矩阵求逆，或采用同伦连续方法以实现全局收敛的效果[20]。

1.2 稳定性

积分方法的数值稳定性条件是指，对于单自由度系统，其迭代放大矩阵的谱半径小于或等于1[21]。为考察精细逐块积分方法的数值稳定性，需考虑如下的线性齐次算例

(13)

其中，ω>0,ξ≥0。

采用Zhong和Williams提出的变换[12]，式(13)可写为

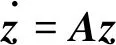
(14)

其中，

应用式(7)～(8)，可得

(15)

相应的放大矩阵为

D=eAh

(16)

显然，放大矩阵D的特征值λ满足

|λI-eAh|=0

(17)

在不考虑Taylor展开截断误差时，求得特征值为

(18)

显然，对于ξ≥0，特征值λ常满足|λ|≤1。当考虑Taylor展开截断误差时，如文献[15, 22]所指，子步长τ趋近集中。Wang[15]指出，在这种情形下，截断阶数q=4、5和二分阶数N=20对于大多数结构而言均可保证稳定性，只有在选取相对系统无阻尼固有周期的大子步长时，才会出现不稳定的结果。

1.3 精度

简便起见，考虑形如g(t,z(t))=G(t)z(t)的线性案例。对于初值问题，定常系统的精细积分数值解接近计算机的精度[13]。因此，精细逐块积分的误差满足

(19)

(20)

其中

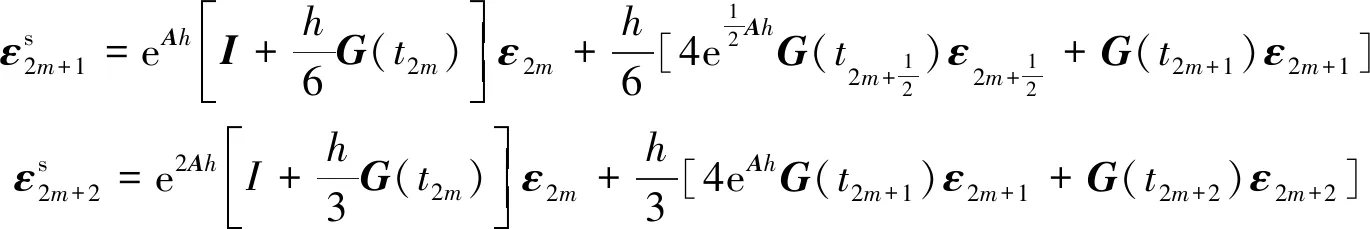
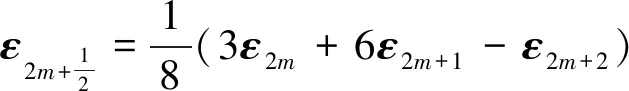
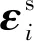
为进一步验证以上结论，考虑如下的单自由度线性系统

(21)

其中，ω=1.0，ξ=0.05，其解析解为

x=e-ξt(c1cosηt+c2sinηt)+s1cosπt+s2sinπt

(22)

其中，

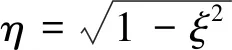
表1对比了精细逐块积分方法、精细积分方法[12]的数值解和系统的解析解。当步长为0.01s时，相比于解析解，精细逐块积分方法可以精确至6位有效数字，高于精细积分方法。表2列出了精细逐块积分方法在不同步长下的误差。可以看出，当步长减半时，误差约缩减为1/16，这与上述收敛阶数的结论非常吻合。

表1 单自由度系统的数值解(0s至1s)

表2 不同步长下精细逐块积分方法的误差

2 数值算例

为验证精细逐块积分方法的有效性，本部分给出了3个算例。

2.1 算例I

考虑两自由度Fermi-Pasta-Ulam问题[23]。如图1所示，系统包含一刚性线性弹簧和两个非线性软弹簧。本系统存在高频振荡，其Hamilton函数为

(23)

其中，qi和pi(i=1,2)分别为广义坐标和广义动量矩。相应的Hamilton正则方程为

(24)

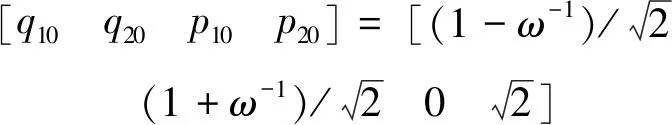
图1 两自由度Fermi-Pasta-Ulam问题Fig.1 The 2-DOF Fermi-Pasta-Ulam problem

令ω=50，用精细逐块积分方法求解式(24)。设置绝对误差和相对误差均为10-14，将Matlab求解器ode15s的求解结果作为参考解。表3列出了经精细逐块积分方法、四阶Runge-Kutta法(RK4)和Newmark方法解出的q1值。可以看出，精细逐块积分方法在步长设置为0.001s时具有9或10位有效数字的精度；当步长增大为0.005s时，精细逐块积分方法仍然具有7位有效数字的精度。然而，在设置步长为0.001s时，RK4方法只有6位有效数字的精度；Newmark 方法直到步长小至0.0001s时才有所收敛，并且只有1或2位有效数字的精度。

表3 经ode15s、精细逐块积分方法、RK4法和Newmark方法求得的q1值

图2绘出了上述3种方法从0至80s的时间历程响应。精细逐块积分方法和RK4法的步长为0.01s，Newmark方法的步长为0.0001s。显然，Newmark方法在步长小至0.0001s时仍然不稳定，而精细逐块积分方法和RK4法可以获得稳定解。然而，如表3所示，虽然RK4法看起来长时稳定，但不如精细逐块积分方法精确。

2.2 算例II

考虑变系数非线性周期系统[24]

(25)

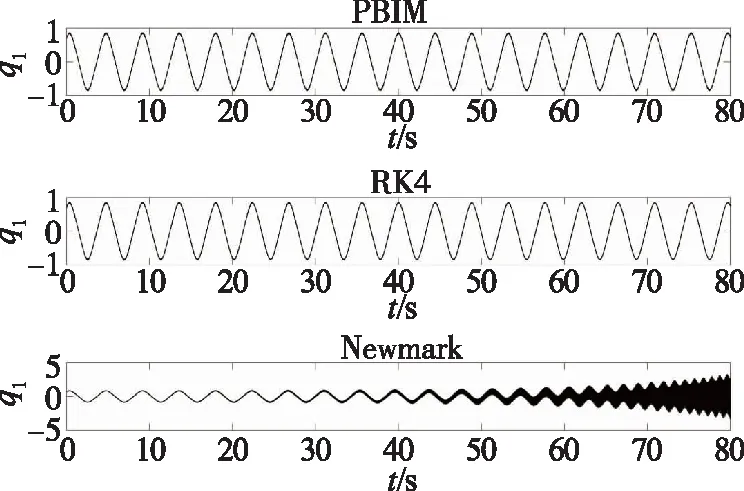
图2 经精细逐块积分方法、RK4法和 Newmark方法求解的q1响应Fig.2 Responses of q1 by the PBIM, the RK4 method and the Newmark method

其Galerkin解为

(26)

其精度可达10-5，可认为是参考解。分别应用精细逐块积分方法、RK4法和Newmark方法求解式(25)，将相应的x1数值解的误差绘制在图3至图5中。在图3中，对精细逐块积分方法依次选取步长h=0.1s和h=0.01s。显然，即使步长增大了10倍，相应的误差仍保持在10-5。图4展现了步长依次设置为h=0.1s和h=0.01s时，由RK4法获得的x1的误差。与精细逐块积分方法不同，当步长增大10倍时，误差也自10-2至10-1放大了10倍。Newmark方法的表现最差。如图5所示，Newmark方法要求非常小的步长，直到步长h=0.0001s才可保持数值稳定。

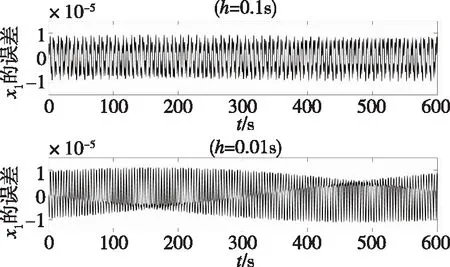
图3 不同步长下精细逐块积分方法的x1的误差Fig.3 Errors of x1 by the PBIM using different step sizes

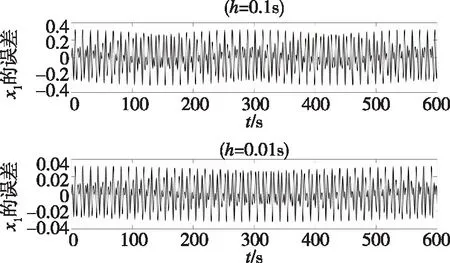
图4 不同步长下RK4法的x1的误差Fig.4 Errors of x1 by the RK4 method using different step sizes

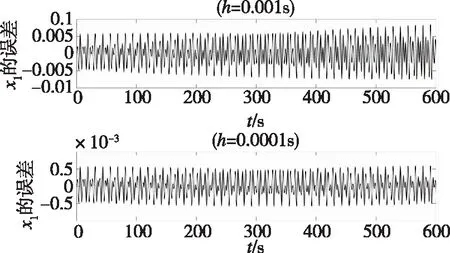
图5 不同步长下Newmark方法的x1的误差Fig.5 Errors of x1 by the Newmark method using different step sizes

2.3 算例III

最后，考虑如下的非线性刚性问题

(27)

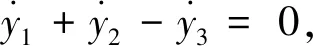
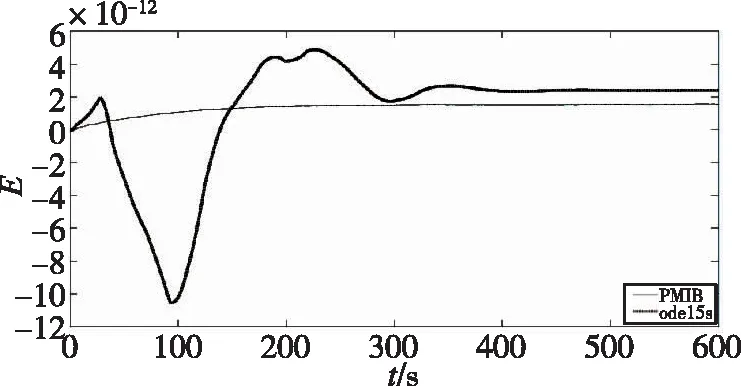
图6 精细逐块积分方法和ode15s求解误差比较(h=0.001s)Fig.6 Comparison of the errors by the PBIM and ode15s(h=0.001s)

3 结论

本文提出了精细逐块积分方法。作为隐式积分格式，此方法可以轻易满足稳定性条件，达到4阶精度。因此，与Newmark方法和RK4法相比，对非线性动力系统应用精细逐块积分方法，可以在大步长的条件下获得高精度和稳定的数值解。此外，由于本方法不需要进行矩阵取逆运算，因此对具有奇异或接近奇异的系统矩阵的问题仍然有效。