可靠性设计优化的球空间设计法*
2019-05-22曹鲁光蔡军亮王冠坤陈振中李晓科吴子豪
曹鲁光,蔡军亮,王冠坤,陈振中,李晓科,吴子豪
(1.上海机电工程研究所·上海·201109;2.中车大同电力机车有限公司·大同·037038;3.东华大学 机械工程学院·上海·201620;4.河南省机械装备智能制造重点实验室·郑州·450002)
0 引 言
经过近40年的发展,可靠性设计优化方法目前已经在工程中(尤其是航天装备等具有高可靠性要求的领域中)被广泛应用;可靠性设计优化方法可以充分考虑复杂航天装备的各类不确定性因素,如加工过程、材料特性、操作环境等,可以显著提高关键核心航天装备的寿命和可靠性,如可以提高卫星姿控飞轮的寿命、导电滑环的可靠性、航天轴承和弹簧等关重件的寿命及复杂飞控系统的稳定性等。在精度都满足要求的情况下,在同等的计算条件下,可靠性设计优化方法是具有更高优化效率的方法,能够减少设计优化所需的时间。尤其对于某些特别复杂的航空航天装备而言,高效率的方法能够节约的时间是很可观的。
典型的可靠性设计的优化模型如下所示:
find:d,μX
min:f(d,μX,μP)
s.t.prob(gi(d,X,P)≥0)≥Ri,i=1,2,…,n
(1)
其中,f()是目标函数,prob()是当前设计点满足第i个概率约束gi()的概率,n是概率约束的个数,d是确定性设计变量,X是随机设计变量,μX是X的均值,P是随机参数,μP是P的均值,Ri表示满足第i个约束的期望概率,上标“Lower”和“Upper” 表示上、下边界。
目前,可靠性设计优化的主要研究方向包括可靠性分析和解耦方法两个方向。可靠性分析方法包括解析法、降维法和模拟法。解析法是基于梯度的方法,包括极值分析法、矩法[1]和基于最大可能失效点(Most Probable Point, MPP)的方法[2]。寻找最大可能失效点的方法是较为有效的,也较为常用,如一次二阶矩法[3]和二次二阶矩法[4]。一次二阶矩法包括可靠度指标法(Reliability Index Approach, RIA)[5]和性能测度法(Performance Measure Approach, PMA)[6]。一些学者提出了其他有效的可靠性分析方法,如先进均值法[7]、混合均值法[8]、圆弧搜索法[9]、增强混合均值法[10]和概率与凸集混合可靠性分析方法[11]、精确分析法[12]。
模拟方法[13-17](如蒙特卡罗法[16])被广泛用于获取高精度的可靠性分析结果。蒙特卡罗法通过大量地抽取样本,判断每一个样本是否发生失效,并统计失效事件发生的比率,从而达到精确模拟的效果[17]。
基于解耦策略的可靠性设计优化方法,主要可分为三类:双循环法、单循环法、解耦法。双循环法包含两个嵌套的循环,其中设计优化循环不断地调用内部可靠性分析循环;单循环法通过某种途径将内部循环进行了消除,如单循环单变量法[18]、单循环法[19],及可信设计空间法[20]。
解耦法将设计优化循环与可靠性分析循环顺序求解,如序列优化与可靠性分析法(Sequential Optimization and Reliability Assessment Method, SORA)[21]、直接解耦法[22]、序列逼近规划法(Sequential Approximation Programming, SAP)[23]、凸线性逼近法[24]、罚函数法[25]、自适应解耦法[26]、最优偏移向量法[27]、混合不确定优化法[28]、区间不确定优化法[29]、非概率鲁棒优化法[30]、概率可行域法[31]及多设计点方法[32]。
可靠性设计优化解析方法的关键在于最大可能失效点MPP的寻找,而MPP点通常位于一个球面上。如果可靠性分析在球坐标中进行,那么在可靠性分析模型中,约束为一个球面,可以将其消除。本文提出一种在球坐标中求解可靠性设计优化问题的方法,该方法可以将优化循环与可靠性分析循环同时进行求解。
本文将首先在第1节中回顾RIA和PMA方法,在第2节中介绍球空间法,在第3节中通过对比算例验证球空间法的有效性,并在第4节中给出结论。
1 可靠性设计优化常用的方法
本节将主要回顾可靠度指标法RIA和性能测度法PMA,这两种可靠性分析方法在双循环方法中最为常用。在可靠性分析过程中,通常需要将相关的、非正态分布的变量X和P转换为独立的、正态分布的变量U(U~(0,1))。一些方法可以实现这种转换:u=T(x,p), or (x,p)=T-1(u),如Rosenblatt 转换[33]和Nataf 转换[34]。
1.1 可靠性指标法(RIA)
在可靠性指标法中, 目标函数是当前设计点的可靠度指标;约束函数是概率约束不大于期望值(假设当Gi(u)≤0时是可行设计)。RIA的数学模型如下:
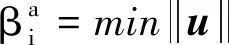
(2)
其中,u是标准设计空间中的随机变量,它是(X,P)由原设计空间转换而来的;Gi(u)是概率约束函数,对应于原设计空间的gi(d,X,P)函数。
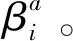
1.2 性能测度法(PMA)
性能测度法也被称为逆可靠性分析法。在标准正态空间中,它将概率约束函数作为目标函数,将期望的可靠度指标作为约束,它的数学模型如下:
(3)
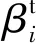
PMA方法在期望的可靠度指标球面上寻找逆最大可能失效点(Inverse Most Probable Point:IMPP),该点具有最大的概率约束函数值(假设Gi(u)≤0时为可行域)。在通常情况下,PMA方法较RIA方法更加稳定,因为它的搜索区域在一个球面或者超球面上。
2 球空间法
逆可靠性分析方法将概率约束函数作为目标函数,将可靠度指标作为约束函数,搜索空间为一个球面Gi(u)≤0,它的模型可以表示为:
find:u
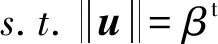
(4)
其中,βt是期望得到的可靠度指标,对应于式(1)中的期望获得的可靠度概率R。
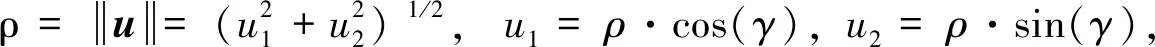
find:γ
min:G(u(ρ,γ))
(5)
可以看出,模型(5)变成了一个无约束的优化问题,相对于带约束的模型(4),它更容易求解。本文提出的球空间法是将可靠性分析模型转换为球坐标来表示,同时可以将可靠性分析循环与设计优化循环并行求解。坐标转换之后,约束函数g(x)变为g(x(ρ,γ))=g(ρ,γ),其中x=(x1,x2,…,xn),(ρ,γ)=(ρ,γ1,γ2,…,γn-1)。
2.1 利用球空间进行可靠性分析
find:γ
min:Gi(u(ρ,γ))
γ1∈(-π,π];γ2,…,γn-1∈(-π/2,π/2]
(6)
其中,u=(u1,u2,…,un)是迪卡尔坐标系下的随机变量,(ρ,γ)=(ρ,γ1,γ2,…,γn-1)是球空间中的对应的随机变量。
(7)
2.2 球空间模型
可靠性设计优化的双循环方法可以表示为式(8)和式(9)。
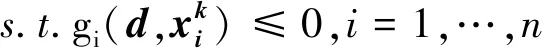
(8)
(9)
在上述模型中,设计优化循环(式(8))和可靠性分析循环(式(9))是嵌套关系,无法将两个循环表达为一个优化循环。
本文将可靠性分析转换为球坐标,从而可以通过极值条件(式(7))对可靠性分析循环进行简化,进而将双循环表示为一个优化循环,即如式(10)所示
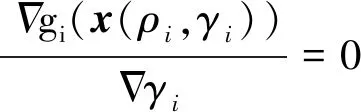
(10)
其中,(ρi,γi)是第i个概率约束在球空间中的IMPP点。
新模型(10)是一个常规的约束优化模型,而且在推导过程中没有近似求解,式(9)中的可靠性分析模型通过极值条件(式(7))进行代替,逆最大可能失效点x(ρi,γi)将通过迭代求解获得。
2.3 球空间法的步骤与流程图
球空间法的步骤与流程图如图1所示,步骤如下所示:

图1 球空间法的流程图Fig.1 Flow chart of sphere design space method
(3)建立可靠性设计优化模型,如式(10),设计变量(d,μX)及角度变量γi都将作为新的设计变量,IMPP点表示为x(ρ,γi);
(4)对式(10)中的约束优化问题进行数值迭代求解,直至设计变量满足收敛条件。
3 应用
在本节中,通过2个算例来验证球空间方法的有效性,对比方法包括双循环法RIA、PMA+、SAP和SORA。计算结果通过蒙特卡罗方法进行验证,样本数量为107。
3.1 数值算例1
该算例为一个非线性数学问题[25],包含两个随机设计变量X1、X2,三个概率约束g1、g2、g3。目标函数为两个变量之和,模型如下
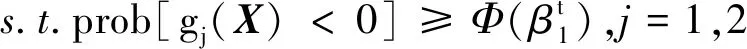
(11)
优化结果如表1所示,可以看出解耦法SORA较双循环法RIA和PMA+效率更高,SAP法具有更高的效率。函数调用次数表示了计算的效率,本文提出的球空间法对于目标函数和约束函数的调用次数均明显减少,具有较高的计算效率。
在比较的5种方法中,所有方法的目标函数值和设计变量值都非常接近。因此,所有算法的求解精度都处于同一水平。表2给出了采用蒙特卡罗法对可靠性进行模拟求解的结果,βi表示第i个概率约束的可靠度指标。所有方法的可靠度指标值都较为接近,这从另外一个角度验证了球空间法与其他方法在精度上处于同一水平。
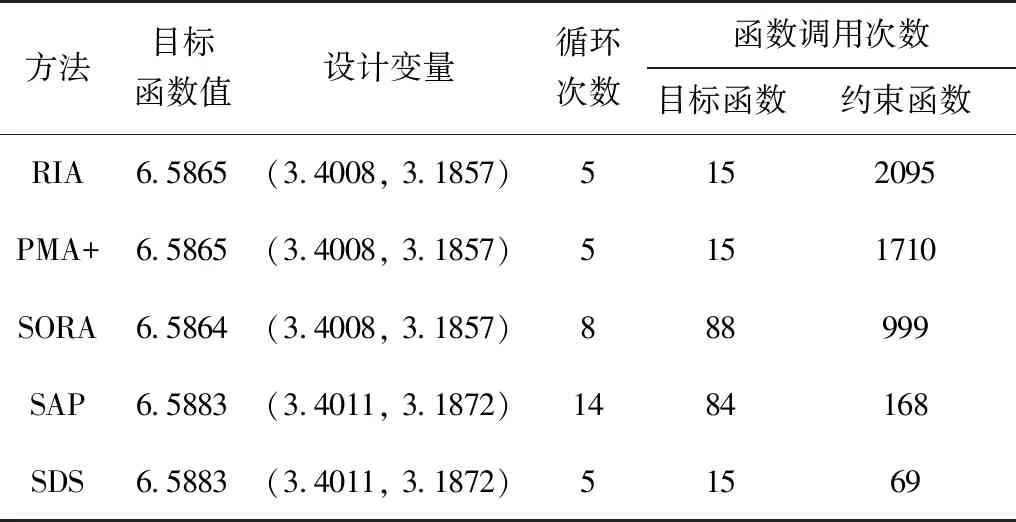
表1 算例1的优化结果
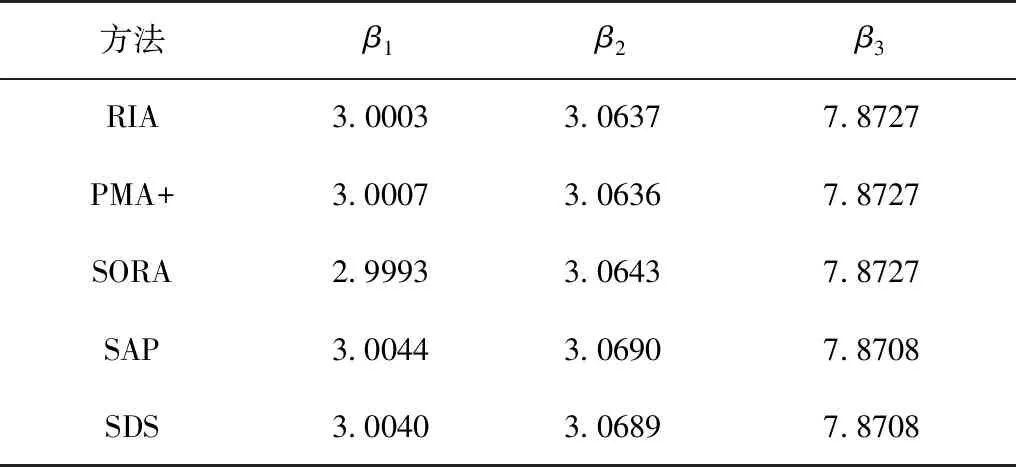
表2 算例1的蒙特卡罗可靠度指标
3.2 数值算例2
该算例[23]有两个确定性设计变量d=[b,h]T,三个随机参数X=[M,F,Y]T,数学模型如下
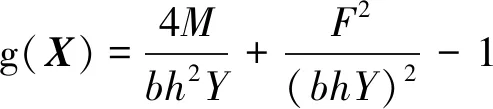
(12)
表3给出了优化结果,所有方法的可靠度指标β1均在2.49附近,目标函数值和设计变量值都几乎相等。因此,所有方法均具有相同的计算精度。在函数调用次数方面,本文提出的球空间法仅需要调用19次目标函数、34次约束函数,远远小于其他方法,因此本文提出球空间法具有更高的求解效率。
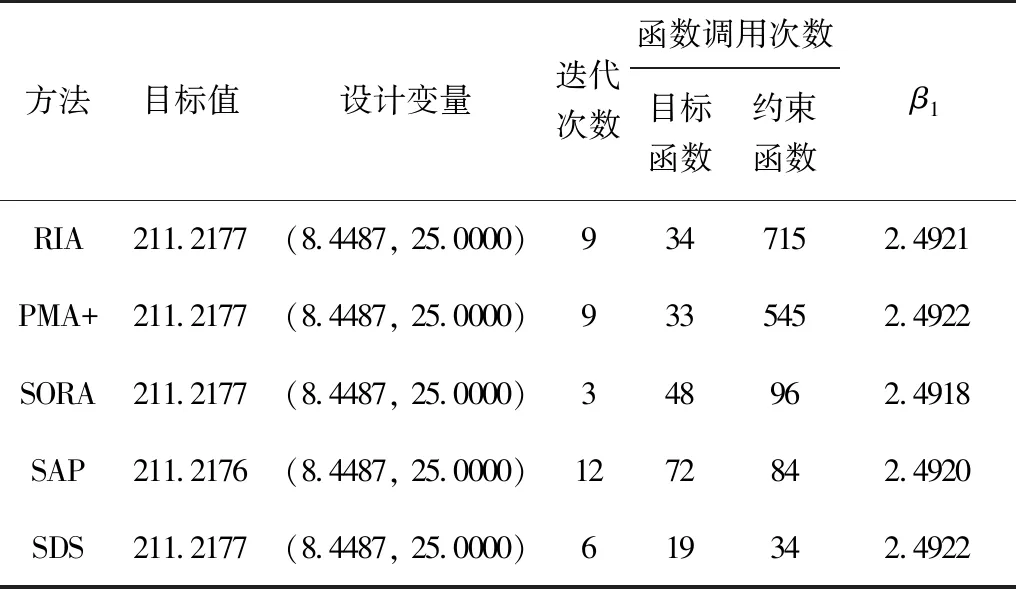
表3 算例2的优化结果
4 结 论
本文提出了一种可靠性设计优化的球空间法,该方法采用球坐标,可以方便地表示逆可靠性分析模型,并将其转化为无约束优化模型,从而可以利用极值条件将内层可靠性分析循环消除,将总的双循环模型变为单循环模型。在新的模型中,设计优化和可靠性分析可以同步进行。
通过算例进行的验证表明,球空间法在计算精度上与其他方法处于同一水平,在求解效率上有明显提升,因此本文提出的球空间法可以作为一种高效的可靠性设计优化新方法。
本文所提出的方法对于复杂装备的可靠性设计优化,如复杂航天飞控装备的可靠性设计,具有显著效果。它将大大缩短可靠性设计的时间,降低整个产品的设计周期,同时保证航天产品的可靠性水平满足设计要求。
