一种基于两级EKF的9-D MIMU/GPS微型无人机组合导航系统的鲁棒性设计*

赵健康，崔 超，朱建斌

(1. 上海交通大学 电子信息与电气工程学院·上海·200240;2.深圳高速工程顾问有限公司·深圳·518094)

0 引 言

随着微型无人机技术的发展与无人机行业的爆发式增长，基于9轴微型惯性测量单元(9 Degree of Freedom Micro Inertial Measurement Unit,9-D MIMU)与全球定位系统(Global Position System, GPS)的低成本组合导航系统日益成为了工程研究与应用的热点[1-2]。

9-D MIMU以成本低廉的优势被广泛应用于消费级无人机系统，但由于其测量噪声过大，仅能在很短的时间内对载体的运动状态进行有效的测量与估计。GPS定位技术成熟，能在较长时间内保持测量数据的稳定并维持一定程度的精度。鉴于此，科研及工程人员设计了诸多将9-D MIMU与GPS的测量数据有效融合的组合导航算法，进而估计出较为准确的载体运动状态。在实际应用过程中，加速度计与陀螺仪的误差标定已经能够满足中低端的应用需求，而磁强计的测量过程容易受到自身制造误差及不确定的外界扰动的影响，给组合导航算法的稳定性与可靠性带来了一定的压力。如何设计鲁棒性算法、有效地降低磁强计的传感器的测量误差对导航状态估计的影响，便成为了研究人员关注的重点。文献[3]提出了使用椭球模型来对磁强计的测量噪声进行建模，取得了良好的磁强计误差修正效果；文献[4]利用陀螺仪的测量值进行了辅助，实时修正了磁强计的误差参数；文献[5]使用两个磁强计互补的原理消除了磁强计不规律和长期的误差干扰；文献[6]采用优化的方法，利用全球导航卫星系统(Global Navigation Satellite System, GNSS)的信息和加速度信息消除了磁场的干扰对导航系统的影响。

上述方法均能取得一定的效果，但是文献[3-4]并未考虑磁倾角和磁偏角对导航系统的影响；文献[7]建立在双磁强计的基础上，而多数硬件平台不满足改造条件；文献[6]利用了优化的方式，同时利用了GNSS信息和加速度计信息来减小磁强计所受干扰对导航系统的影响，实验效果虽然良好，但是其优化算法的计算量大，不便于在低成本的嵌入式平台上实现。本文在椭球模型修正磁强计的基础上，提出了一种基于两级扩展卡尔曼滤波器(Extended Kalman Filter，EKF )的9-D MIMU/GPS微型无人机组合导航系统的鲁棒性设计：首先，建立第一级EKF，融合加速度计、陀螺仪和GPS的速度观测信息，估计出载体坐标系下的单位重力矢量；而后，利用单位重力矢量将修正后的磁强计测量值正交单位化，消除磁倾角的影响；最后，建立第二级EKF，将正交单位化的磁强计测量数据和GPS的位置、速度信息作为观测量，将载体的姿态、速度、位置及9-D MIMU的误差作为状态量进行有效的估计。实验仿真结果表明，本文的算法设计能够针对性地降低磁强计原始测量数据中包含的误差对导航系统的影响。

本文的组织结构如下：第2小节推演了系统模型和算法步骤，第3小节展示了仿真和实验结果，第4小节总结了本文的内容。

1 理论背景

1.1 坐标系定义

为了能够更加清晰地描述各个传感器的测量模型和标定方法，我们首先定义本文所使用的坐标系：载体坐标系(b )与9-D MIMU传感器固连，xb指向载体前方并与横滚角φ关联，yb指向载体右方并与俯仰角θ关联，zb指向载体下方并与偏航角ψ关联；取“北-东-地(NED)”坐标系作为导航坐标系(n )，xn指向当地北方，yn指向当地东方，zn指向地球表面并竖直向下。

1.2 传感器测量模型

由于微型无人机体积小、载荷有限，因此只能用低功耗、低成本的传感器来构造导航系统。基于微机电系统(Micro-Electro-Mechanical System, MEMS)技术的9-D MIMU芯片，集成了三轴磁强计、加速度计和陀螺仪，被广泛应用于微小型无人机的设计。此外，为了能够实现无人机在室外的定点飞行、航迹规划等高级任务，无人机需要搭载专用的GPS模块来为其提供位置、速度信息。下文将分别描述4种传感器的测量模型。

1.2.1 磁强计

磁强计可以敏感并测量传感器周围的磁场环境，包括地磁场和其他磁场干扰。三轴磁强计的测量模型[3]可以表述为

(1)

Mm-error=Mm-nonOrthMm-scaleMm-soft

(2)

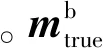
1.2.2 陀螺仪

陀螺仪可以敏感并测量载体的三维旋转角速度，其测量模型可以表示为

(3)

Mgyro-error=Mgyro-alignMgyro-nonOrthMgyro-scale

(4)

式中，Mgyro-error是一个3×3的矩阵，描述了陀螺仪与磁强计之间的非对齐误差Mgyro-align、陀螺仪的三轴非正交误差Mgyro-nonOrth和三轴增益误差Mgyro-scale。bgyro表示陀螺仪的常值偏差。εgyro表示陀螺仪的测量噪声，并假设其满足白噪声特性。

1.2.3 加速度计

加速度计可以敏感并测量载体的三轴加速度，其测量模型可以表示为

(5)

Macc-error=Macc-alignMacc-nonOrthMacc-scale

(6)

式中,Macc-error是一个3×3的矩阵，描述了加速度计与磁强计之间的非对齐误差Macc-align、加速度计的三轴非正交误差Macc-nonOrth,以及三轴增益误差Macc-scale。bacc表示加速度计的常值偏差，εacc表示加速度计的测量噪声，并假设其满足白噪声特性。

1.2.4 GPS

由于技术成熟、成本低廉等特点，GPS被广泛应用于汽车、飞行器等室外导航领域，也成为了微型无人机室外飞行的常用传感器。通常而言，GPS接收机可以提供载体所在位置的经度L、纬度B、相对于平均海平面的高度hMSL,GPS，以及载体在导航坐标系(北-东-地)下的速度向量vGPS=[vN,GPS,vE,GPS,vD,GPS]T。为了方便融合各个传感器的测量数据，需要将GPS接收机的各个测量数据转换至导航坐标系中。

记载体起飞地点或自定义的某一地点为起始点Phome(Bhome,Lhome,hhome)，载体在当前位置的GPS位置测量值为Puav(Buav,Luav,huav)。取辅助点Paux(Buav,Lhome)，已知连接Phome、Paux和Puav三点可以构成一个曲面直角三角形。当无人机在小区域内飞行时，可以假设地球为标准球体，通过Haversine[7]公式计算无人机在以起始点为原点的导航坐标系下的位置

(7)

(8)

PD,GPS=huav-hhome

(9)

1.2.5 测量模型简化

由于MEMS技术工艺的限制，并出于降低系统复杂度的考虑，本文将加速度计和陀螺仪的测量模型简化为

(10)

(11)

同时，也忽略GPS模块测量过程中其他误差对测量的影响，假定GPS的测量噪声满足零均值高斯白噪声假设，即有

(12)

(13)

1.3 基于椭球模型的磁强计干扰补偿

在忽略测量噪声nm的情况下，对磁强计的误差修正模型可以由式(1)、式(2)得到

(14)

在较小的飞行区域内，地磁场强度与方向相对恒定，根据式(14)可以得到

(15)

式中，G=(Mm-error)-1。

在没有磁场干扰的情况下，即bm=0，Mm-error=

G=I，I为单位矩阵，真实磁场的测量值分布在一个球心在原点的球面上。对应地，在有磁场干扰的情况下，磁强计的实际测量值应分布在一个中心偏移bm的椭球面上，椭球的形状由Mm-error决定。

式(15)可以进一步整理为

(16)

而椭球是一个二次曲面，其一般方程表示为[3,8]

ax2+bxy+cy2+dxz+eyz+jz2+
px+qy+rz+s=0

(17)

改写为矩阵形式，为

(X-X0)TA(X-X0)=1

(18)

可以展开为

(19)

其中

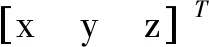
(20)

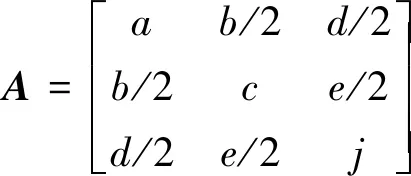
(21)

(22)

将式(16)与式(19)各项对应，可以得到如下关系

(23)

ax2+cy2+jz2+px+qy+rz+s=0

(24)

ax2+cy2+jz2+px+qy+rz+s=0，对应地有

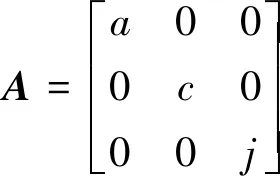
利用磁强计在载体运动过程中的测量数据，拟合得到椭球模型式(24)，就可以对磁强计的测量误差进行补偿。

将式(24)记为

F(a,mb)=0

(25)

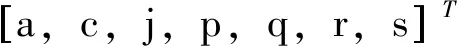
(26)

其中

D=

求解式(26)属于静态约束条件下的极值约束问题，可以利用拉格朗日乘数法求解，构造增广代价函数

(27)

式中，λ为拉格朗日乘数。

对式(27)求偏导数得

(28)

将其置零，并结合约束条件，可以得到

(29)

即将椭球拟合问题转换为矩阵DTD相对于矩阵B的广义特征值问题，最终通过求解得到椭球模型的参数a。然后，利用a和式(21)得到矩阵A。由于A为对角矩阵，容易得到

至此，并利用式(14)来对测量得到的磁强计数据进行修正。

由于矩阵A不受椭球方程常值系数s的影响，利用矩阵G和bm得到的磁强计修正值与真实的磁场强度呈某一固定倍数关系，但不影响磁强计对磁场方向的敏感。

2 两级EKF组合导航系统的鲁棒性设计

完整的系统模型可以分为3个部分：(1)基于加速度计、陀螺仪和GPS速度信息的单位重力向量估计；(2)磁强计测量正交标准化；(3)基于加速度计、陀螺仪、单位磁场矢量和GPS的组合导航。系统模型原理如图1所示。

2.1 单位重力向量估计

加速度能够敏感地球的重力场，但是载体的三轴线加速运动会极大地影响加速度计对重力场的测量。为了能够更好地估计出载体所在环境的重力场，本文设计了一个EKF滤波器，记为EKF A，融合GPS的速度测量值和陀螺仪的角速度测量值，消除载体的线加速运动对重力估计的影响。

系统模型可以用如下微分方程描述。

(30)

式中，符号^表示估计量，·表示导数，q=[q0,q1,q2,q3]T表示导航系与机体系之间相对旋转的四元数，一个四元数由一个实数和一个向量组成，q0表示实数，v=[q1,q2,q3]T表示向量；ω=[ωx,ωy,ωz]T表示机体坐标系下陀螺仪的测量数据；V=[vN,vE,vD]T为导航系中载体的运动速度；fb=[fx,fy,fz]T表示机体坐标系下加速度计的测量数据；g表示当地重力加速度向量；bgyro=[bgyro,x,bgyro,y,bgyro,z]T和bacc=[bacc,x,bacc,y,bacc,z]T分别为陀螺仪和加速度计的三轴测量偏差估计值。

根据式(30)所示的微分方程，将EKF A的状态向量定义为

(31)

将量测向量定义为

Z=[vN,GPSvE,GPSvD,GPS]T

(32)

将量测模型描述为

[vN,GPSvE,GPSvD,GPS]T=[vNvEvD]T

(33)

基于式(30)、式(31)、式(32)、式(33)，可以利用扩展卡尔曼算法将模型线性化，并迭代估计出导航状态量[11]。

由式(30)可知，EKF A没有利用磁强计的数据，可以通过对载体速度的观测，来消除载体线加速度对姿态的影响。同时，利用估计出的四元数构建旋转矩阵

(34)

进而求得单位重力向量的估计

2.2 磁场矢量正交标准化

地球磁场的方向并非严格指北，还存在着磁偏角和磁倾角的影响[10]，因此北半球的实际地磁场矢量除了北向分量外，还包含东向分量和竖直向下的分量。本文基于水平方向磁场矢量与重力向量相互垂直的关系，设计了如下方式来获取与单位重力向量正交的单位磁场矢量，消除磁倾角对导航系统的影响。

(35)

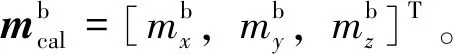
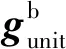
(36)

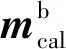
(37)

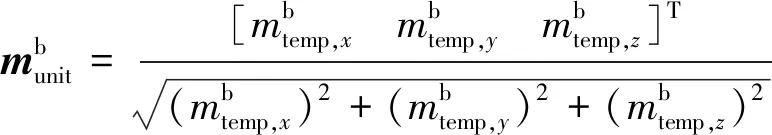
(38)

显然，当载体坐标系与导航坐标系重合时，有

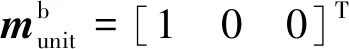
2.3 组合导航系统设计

为实现各个传感器的特性互补，本文设计了EKF滤波器将全部传感器的测量值融合到导航系统状态的估计中，并将其记为EKF B。

系统模型可以用如下微分方程描述

(39)

根据式(39)所示的微分方程，将EKF B的状态向量定义为

(40)

将量测向量定义为

可将量测模型描述为

(41)

式中，C(ξ)为磁偏角修正因子，ξ表示磁偏角，用来修正地理北极与地磁北极之间的误差，C(ξ)可以用矩阵表示为

(42)

与EKF A类似，基于式(30)～式(33)，可以利用扩展卡尔曼算法将模型线性化并迭代估计出导航状态量[11]。

运动过程中的微型无人机的航向信息可以通过载体在导航系中的速度及磁强计计算获得；而处于悬停状态或缓慢运动状态的无人机则仅能依靠磁强计来获取当前的航向。因此，磁强计对微型无人机的航向及其他状态的正确估计起到了至关重要的作用。

为了能够在磁场异常的情况下依然能够维持微型无人机导航系统的基本功能，使异常的磁场测量数据不对导航系统中其他状态量的估计产生污染，有必要建立磁场异常判别机制，以便在进行多传感器数据融合时减小其权重。

依据式(24)、式(25)，F(a,mb)表示数据点到椭球面的距离，当椭球模型能够对当前磁强计的测量值进行理想的修正时，则有F(a,mb)=0；当磁强计的测量受到其他磁场噪声的干扰时，F(a,mb)将会与零值产生一定的偏差。定义磁强计的当前测量值与椭球校正模型的适配指数为

ξ=e|F(a,mb)|

(43)

ξ越接近于1，说明磁强计的当前测量值越能与椭球校正模型契合；否则，说明当前磁强计受到了其他额外异常的磁场噪声的干扰。为了隔离异常的磁强计测量值，本文利用式(43)构造了方差膨胀因子，依据ξ的大小和自定义的临界异常参数TD、k1、k2，将磁场异常程度划分为正常、临界异常和严重异常3个等级

(44)

相应的磁强计测量值的等价协方差矩阵为：

(45)

3 仿真实验及结果分析

3.1 磁强计椭球模型修正实验

本小节设定三轴磁强计的模型误差为

仿真数据利用随机的姿态四元数模拟不同的载体姿态，并结合磁强计的误差模型得到仿真的磁强计的输出。图2为磁强计原始测量数据的椭球拟合立体视图，可以看到由于模型误差的存在，磁强计的测量点分布在一个椭球的表面上。

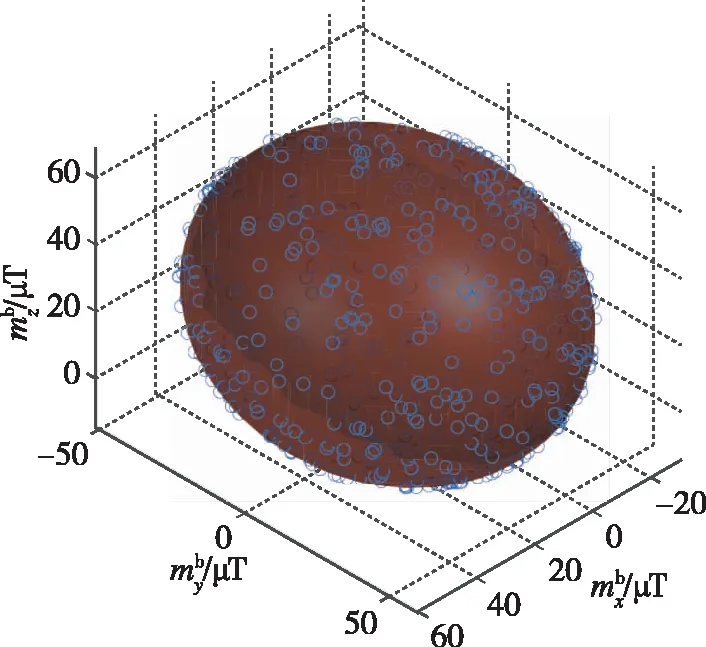
图2 磁强计原始测量数据的椭球拟合立体视图Fig.2 Stereo view of the original measurement data of magnetometer based on ellipsoid fitting

经过本文1.3小节的算法校正，求解结果为

可见本文对磁强计的校正算法能够有效估计磁强计的误差模型参数。图3给出了校正后的磁强计测量数据的椭球拟合图。可以看到，磁强计的输出数据已经被较好地校正成为球体，说明基于椭球模型的修正能够降低磁强计在测量时被引入的误差。

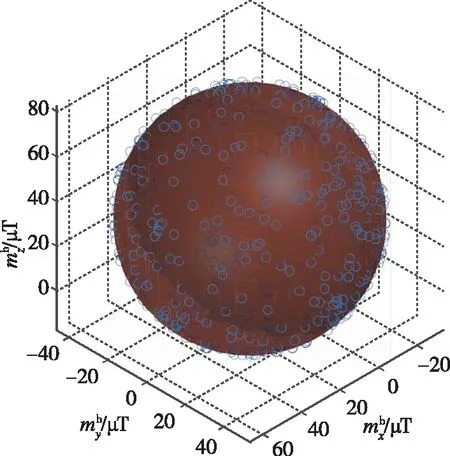
图3 经椭球模型校正后的立体视图Fig.3 Stereo view of the measurement data of magnetometer corrected by ellipsoid model

3.2 导航姿态信息估计实验

为了验证基于磁强计椭球校正模型所设计的抗差卡尔曼滤波器的鲁棒性，本文将导航系统的姿态估计作为研究重点，并基于参考导航数据集中的位置、速度及载体姿态角等信息，利用1.2节各个传感器的测量模型，仿真生成了陀螺仪、加速度计、磁强计和GPS的测量数据，并在磁强计的测量数据上选取测量区间[2000，3000]叠加了正弦波干扰，用来模拟载体在飞行过程中所受到的缓慢变化的磁场的干扰。图4展示了三轴磁强计上所叠加的测量噪声，图5展示了叠加正弦波噪声后的磁强计测量值。

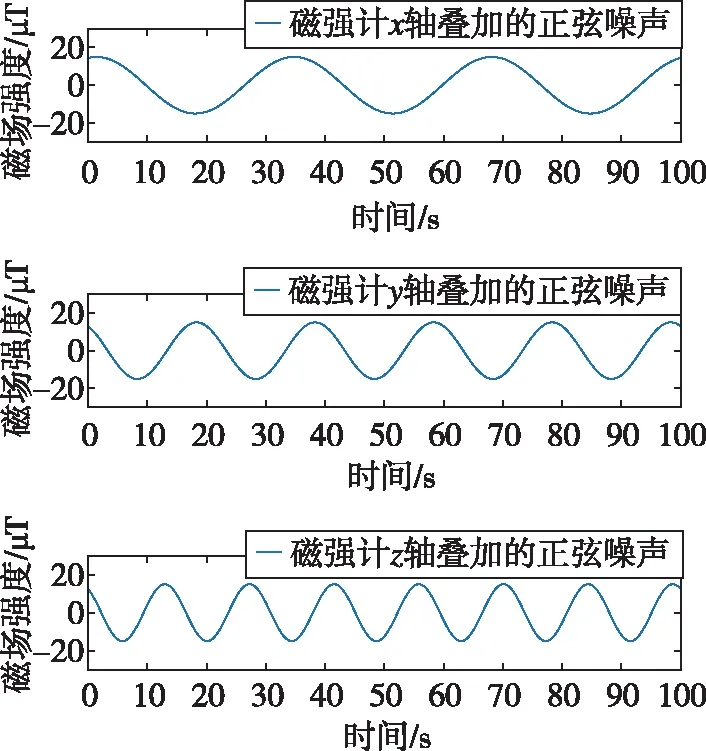
图4 正弦波形式的磁场干扰Fig.4 Sinusoidal magnetic field interference

图5 受正弦波干扰的磁场测量值与原始值的对比图Fig.5 Comparison of magnetic field measurements disturbed by sinusoidal noise with original values

在仿真实验中，首先使用基于式(39)所描述的微分模型设计EKF算法，来解算各个导航状态量，滤波器的参数如表1所示。从图6可以看出，由于磁强计测量量上所叠加的正弦波的干扰，导航系统的姿态估计结果相应地出现了波动。与此对比，本文基于磁强计的椭球模型来对异常的磁强计测量值进行判别，设计抗差EKF算法估计各个导航状态量，滤波器参数与表1相同，估计结果如图7所示。对比两种算法的估计结果，显然后者能够有效抑制异常磁场测量值对导航系统的影响，得到更加可靠、稳定的导航状态量的估计值。

表1 EKF算法参数

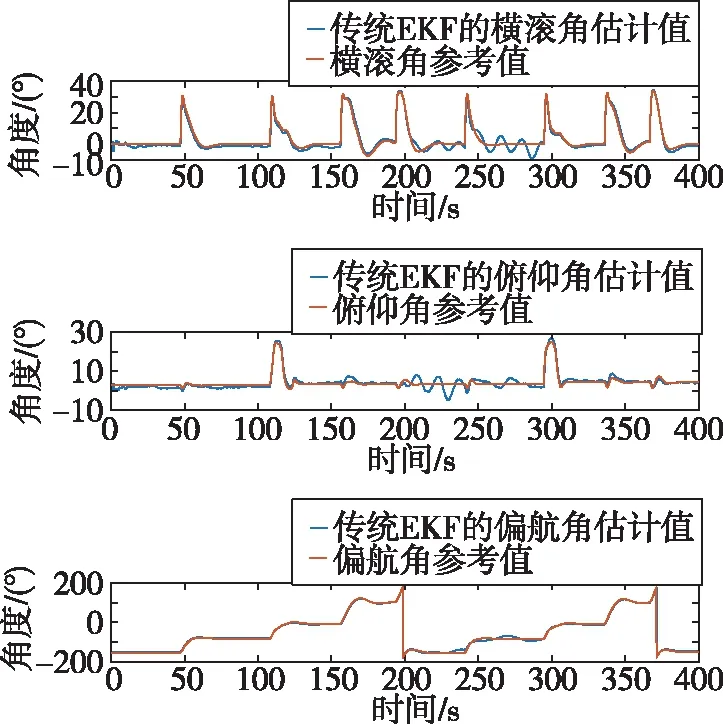
图6 受正弦波噪声干扰的三轴姿态解算结果与 参考值的对比图Fig.6 Comparisons between the calculated results of three- axis attitude disturbed by sinusoidal noise and the reference values

图7 基于抗差EKF求解的三轴姿态解算 结果与参考值的对比图Fig.7 Comparisons between the results of three-axis attitude calculation based on robust EKF esti- mation and the reference values

4 结 论

本文针对磁强计在低成本微型无人机上应用时容易受到外界干扰，并影响导航系统其他状态量的准确估计的问题，提出了一种基于两级EKF的9-D MIMU/GPS微型无人机组合导航系统的鲁棒性设计。利用磁强计的椭球模型对磁强计的测量误差进行了建模，校正了磁强计在消费级微型无人机导航系统中的主要误差项，并建立了磁强计测量异常判别机制，增强了导航系统的鲁棒性。实验表明，本文对导航系统的设计能够有效校正磁强计原始测量数据中所包含的误差，降低导航系统对异常磁场测量的敏感程度。