混合删失样本下的Frechet分布参数估计

祁 辉，廖逢钗，李淑婷，唐必成

（1．三明学院 信息工程学院， 福建 三明365004；2．数字福建工业能源大数据研究所， 福建 三明365004；3．工业大数据分析及应用福建省高校重点实验室， 福建 三明365004；4．物联网应用福建省高校工程研究中心， 福建 三明365004）

Frechet 分布是一种重要的寿命分布。它是由Frechet[1]在1927年发布的一篇关于极大值的渐近分布的论文中提出。Frechet 分布在实际中有重要的应用, 例如可以用来分析自然灾害造成地损失, 某种新型病毒的传播速度等。对于产品的寿命T 服从两参数的Frechet 分布, 其概率密度函数和分布函数表示如下:

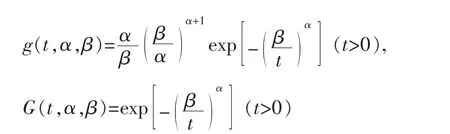
其中α＞0 称为形状参数, β＞0 称为尺度参数。

关于Frechet 分布的性质和应用, 已有许多学者进行了研究。其中Mann[2]研究了三参数模型下的Weibull 分布以及Frechet 分布的估计问题。Harlow[3]鉴于Frechet 分布在不同领域的应用，提出该分布也是工程研究中是一种非常实用的分布。Nadarajah 和Kotz[4]在社会学研究模型中引入Frechet分布。Abbas 和Tang[5]研究了形状参数已知的情况下, Frechet 分布中尺度参数的贝叶斯估计、极大似然估计和概率加权矩估计。骆正山等[6]讨论了将Frechet 分布用于海底油气管道腐蚀的评价与预测。曾林蕊等[7]讨论了定数截尾样本下Frechet 分布中参数的近似极大似然估计。何亮和徐晓岭[8]将Frechet 分布应用于加速寿命试验, 并利用极大似然估计以及MPS 估计、 最小距离估计方法对参数进行估计。

1 混合删失模型

样本数据的删失常出现于寿命观测和可靠性试验中, 由于样本中的个体无法被观测或者实验中途停止, 导致样本数据删失的情形。样本数据删失类型主要有以下3 种: Ⅰ型删失, II 型删失以及混合型删失。I 型删失的特点就是删失时间是固定的, 即对所有个体的观察停止在一个时间T, 这类删失也称为定时删失。II 型删失的特点事先有一个故障次数r, 若同时对n 个个体进行观察, 直到有r（r＜n）个体死亡（故障）为止, 样本数据被删失。

基于混合删失下样本的寿命数据描述如下: 假定从总体中随机抽取容量为n 的样本进行测试,当实验失败次数达到事先确定次数r（r＜n）时或者实验时间达到事先确定的时间T 时, 实验结束。因此, 在混合删失情形下, 实验时间和实验失败次数分别不会超过T 和r。令X1，X2, …，Xn为样本中n 个个体的寿命, X1：n＜X2：n＜…＜Xn：n为相应的顺序统计量, 实验观察时间和实验失败次数分别记为随机变量C=min（Xr：n，T）和D, 则混合删失下样本为（X1：n，X2：n，…，XD：n，C,D）。特别是当D=0 时, 没有失败的信息会被观察到, 但由于实验时间存在删失变量, 因此个体寿命X（D+1）：n，X（D+2）：n，…，Xn：n一般不会被完全观测到。

相比Ⅰ型和Ⅱ型删失模型, 混合删失模型在实际运用中更灵活, 已成为众多学者的研究对象。Chids 等[9]研究了基于混合删失样本下指数分布的似然估计, Kundu[10]考虑了Weibull 分布在混合删失样本下的统计推断, Kundu 和Pradhan[11]讨论了混合删失样本下广义指数分布的参数估计, Dube等[12]研究了混合删失样本下对数正态分布的估计问题, Dey 和Pradhan[13]研究了混合删失样本下的广义倒指数分布。鉴于Frechet 分布寿命观测和自然灾害分析中的重要应用, 为此, 研究了混合删失样本下的Frechet 分布的参数估计问题。

2 极大似然估计

在混合删失样本下, 考虑Frechet 分布的极大似然估计, 令c, d 分别表示随机变量实验观察时间C 和实验失败次数D 的观察值, 那么, 极大似然函数可以表示为:

由于分布函数中尺度参数做为分布类标识, 因此, 考虑尺度参数β 已知的情形下形状参数α 的估计, 不妨设β=2, 则极大似然函数可以表示为：

取对数, 可得对数似然函数:

两边同时对α 求导, 可得:

对于似然方程：

由于上式似然方程的复杂性, 无法利用一般的求解方法得到结果。从可编程性考虑, 牛顿迭代法操作简单, 每次迭代都是简单的机械化运算, 易于编写算法程序。因此, 运用牛顿迭代法对混合删失下Frechet 分布的似然方程进一步求解, 算法步骤如下：

取其中的线性部分用来作为非线性方程f（α）=0 的近似方程,则有:

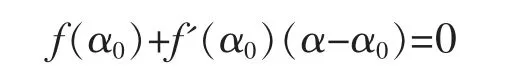
设f'（α0）≠0，则其解为:

求出a1附近f（α）的泰勒展开式, 再取其线性部分作为f（α）=0 的近似方程。若f'（α1）≠0, 则得:

这样, 得到牛顿(Newton-Rapfson)算法[14]的一个迭代的关系式:

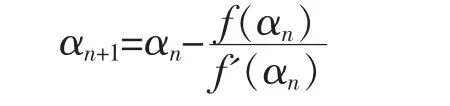
当达到迭代次数n 或者误差不超过给定ε 时, 迭代停止, 求出似然方程的近似解α^。

3 随机模拟

通过随机模拟来验证所提出的估计方法的正确性。首先,从尺度参数β=2 的Frechet 总体中抽取容量为n=30 的简单随机样本X1，X2，…，Xn,样本的容量n 分别为30,50 以及80 不等。考虑到混合删失的情形,假定删失时间变量T 在每种抽样容量下分别取大小不等3 个值,以此来逐步提高删失率。删失次数变量分别取不等3 个值为：0.8, 1.5, 3, 以此来区分删失率。当形状参数真值α=0.8, 基于500 次的模拟结果见表1～3, 当形状参数真值, 基于500 次的模拟结果见表4～6。

表1 当α=0.8、T=0.8 时估计量的随机模拟结果

表1 当α=0.8、T=0.8 时估计量的随机模拟结果

n 30 50 80 r 10 15 25 20 30 40 40 50 60 mean α 0.9150410 0.8869617 0.9070617 0.8677661 0.8593394 0.8439460 0.8217997 0.8255935 0.8298795 rmse α 0.2384779 0.1946554 0.2211332 0.1602285 0.1417189 0.1321461 0.1024124 0.1042219 0.1029260

表2 当α=0.8、T=1.5 时估计量的随机模拟结果

表2 当α=0.8、T=1.5 时估计量的随机模拟结果

n 30 50 80 r 10 15 25 20 30 40 40 50 60 mean α 0.9056136 0.8885545 0.8932017 0.8396100 0.8465484 0.8450863 0.8331837 0.8323408 0.8328658 rmse α 0.2381911 0.2227183 0.2293879 0.1489262 0.1408064 0.1568668 0.1015955 0.1110191 0.1124685

表3 当α=0.8、T=3 时估计量的随机模拟结果

表3 当α=0.8、T=3 时估计量的随机模拟结果

n 30 50 80 r 10 15 25 20 30 40 40 50 60 mean α 0.8452288 0.8301479 0.8400956 0.8384349 0.8138544 0.8241999 0.8098737 0.8134814 0.8032727 rmse α 0.16797170 0.15646270 0.16193770 0.12630400 0.12010790 0.11516640 0.08853260 0.08640164 0.08404830

从表1～3 的中形状参数估计量的统计指标:估计量的均值（mean）,估计量的均方误差（rmse）可以看出, 当删失次数变量r 固定时, 随着样本容量n 增大, 在同等删失率下, 估计结果越来越好; 当删失次数变量r 和样本容量n 均固定时, 随着删失时间变量T 的增大,删失率提高, 估计量仍然表现良好。即使在n=30 的小样本情形下依然成立。对比表1～3, 当删失次数变量r 逐渐增大, 删失率降低, 在同等情形下, 估计量的估计结果表现得更好。

当形状参数α 真值增大到2 时, 由随机模拟的结果表4～6 可以看出, 上述情形仍然成立, 估计量的统计结果仍然表现良好。

表4 当α=2、T=0.8 时估计量的随机模拟结果

表4 当α=2、T=0.8 时估计量的随机模拟结果

n 30 50 80 r 10 15 25 20 30 40 40 50 60 mean α 1.783388 1.791919 1.789607 1.789686 1.798035 1.778554 1.833184 1.824481 1.832820 rmse α 0.2008732 0.2011010 0.2109656 0.1382963 0.1308918 0.1338026 0.1125829 0.1122783 0.1024405

表5 当α=2、T=1.5 时估计量的随机模拟结果

表5 当α=2、T=1.5 时估计量的随机模拟结果

n 30 50 80 r 10 15 25 20 30 40 40 50 60 mean α 2.226087 2.273969 2.224721 2.146189 2.137436 2.140004 2.096855 2.088440 2.081841 rmse α 0.5626685 0.5921566 0.5199464 0.3961160 0.3631685 0.3610385 0.2674839 0.2716929 0.2746031

表6 当α=2、T=3 时估计量的随机模拟结果

表6 当α=2、T=3 时估计量的随机模拟结果

n 30 50 80 r 10 15 25 20 30 40 40 50 60 mean α 2.161996 2.056156 2.029569 2.069200 2.041950 2.019589 2.024157 1.998279 1.982394 rmse α 0.4424088 0.3748913 0.3446413 0.2943757 0.2797575 0.2543793 0.2225639 0.1970202 0.1793307

4 结论

对于混合删失样本下的Frechet 分布, 考虑尺度参数β 已知的情形下形状参数α 的极大似然估计, 随机模拟结果显示上述估计方法具有良好的性质。此外, 如何在尺度参数β 和形状参数α 均未知的情形下构建新的算法求解似然方程组值得进一步进行研究。下一步,考虑构造Frechet 分布的对数似然函数Fisher 信息矩阵, 利用迭代算法, 求解Frechet 分布尺度参数β 和形状参数α 的估计。