石油化工装置长周期运行风险超早期精确预警方法
2019-05-21胡瑾秋张立强张来斌
胡瑾秋, 张立强, 张来斌
(中国石油大学(北京) 油气资源与探测国家重点实验室 机械与储运工程学院, 北京 102249)
安全预警技术早已被广泛应用到各石油化工企业之中。安全预警通过分布式控制系统(DCS)采集的数据,对关键参数进行多方位的综合分析,实时捕捉装置运行过程中存在的异常现象[1]。但这类报警方法会因噪声及采集误差导致大量错误报警,且不能提前发出警告[2]。现有的预警方法主要包括主元分析的方法和参数预测的方法,齐咏生等[3-5]基于传统的主元分析方法,改进了主元选取方法及统计量的计算方法,实现故障的预测。但主元分析方法面对数据变化不太明显的异常时,会有很高的漏报率。Wang等[6]运用经验模态分解(EMD)方法对非稳态的时间序列进行分解,并进行多步前向预测,但这类方法仍属于短期预测。Chang等[7]提出了化工过程装置的风险预警系统,运用定性方法对装置的风险值进行打分,但该方法无法准确表达异常工况产生的风险值。
针对以上问题,笔者开展了针对化工过程预警技术的研究。提出了运用故障链预测炼化装置故障发生后状态;应用灰色关联分析法和卡尔曼滤波法实现多参数关联预警;以及运用粒子群优化最小二乘向量机预测过程参数实现预警等有效的预警方法[8-10]。
在此基础上,笔者针对石油化工装置长周期运行风险超早期精确预警方法开展了相关研究,提出基于损失函数的石油化工装置风险预警方法。损失函数通常用于精确描述目标偏移与预期损失之间的关系,运用损失函数,计算参数偏差可能造成的预期损失,并运用剩余时间模型计算异常工况发生的可能概率,从而得到该参数偏差所产生的风险,通过监测风险值的变化实现装置的风险预警。经过案例分析,相比DCS系统,该方法可提前10 min左右监测到异常工况,实现了异常工况的有效预警,为控制石油化工生产过程中异常工况的产生提供了指导。
1 风险预警方法的基本原理
1.1 损失函数构造
损失函数根据其应用范围不同分为许多种类,常见的如平方损失函数、加权损失函数、转置正态损失函数等。Hashemi等[11-12]总结了不同损失函数的特性及对损失的刻画能力。考虑石油化工装置参数与实际值的随机偏离,笔者采用修正型转置正态损失函数。该损失函数可以通过调节形状因子修正损失函数的形状,从而更好地刻画实际损失。损失函数L如式(1)所示:
(1)
式(1)中,y为状态参数值;Δ为能够造成最大损失的参数值到参数目标值的距离;γ为形状因子;T为状态参数目标值。损失函数的变化范围0≤L≤1。
根据实际情况的不同,可以得到不同的形状因子,从而构造出与待测参数相匹配的损失函数,进而准确描述参数偏差带来的预计损失。由式(1)可以看出,当参数处于目标值时,损失值为0,参数偏离目标值越远,损失值越大。
1.2 异常工况发生概率计算
运用剩余时间理论对异常工况发生概率进行计算[13],该理论通过计算状态参数到达报警阈值所需要的时间,对装置的安全性进行量化。剩余时间越多,则能够对异常状态采取的措施越充分,装置的安全性越高;反之,剩余时间越少,则更难以对异常状态采取完善措施,异常工况的发生概率就会越高。
剩余时间t的表达式如下所示:
(2)
式(2)中,ylim为状态参数阈值;ΔV为状态参数的瞬时变化率,该参数可用最小二乘法对数据曲线进行拟合,并对拟合多项式进行一阶微分计算求得[14],最小二乘法的计算步骤如下。
如式(3)所示,x为状态参数对应的时间,S;a为系数。通过最小二乘法确定最优ai,使得在各个点的偏差δ平方和最小,从而得到精确的拟合多项式。
f(x)=anxn+an-1xn-1+…+a1x+a0
(3)
将k对数据(xi,yi)带入式(3)中,得到如下方程:
(4)
将式(4)转换成矩阵的形式,求得矩阵的唯一1组最优近似解,使得偏差δ的平方和最小,从而得到最小二乘拟合多项式。对得到的最小二乘多项式进行一阶微分计算,得到ΔV。
异常工况发生的概率密度函数f(t)如式(5)所示:
(5)
式(5)中,t为剩余时间;e为自然常数;λ为状态参数变化过程中允许剩余时间倒数,其表达式如式(6)所示:
(6)
式(6)中,ΔVt为参数最大允许变化率,取正常工况下参数变化速率最大值,即max(ΔV), 对一个确定的状态参数而言,ΔVt是常数。
根据式(2)、式(5)、式(6),异常工况发生概率P如式(7)所示:
(7)
1.3 参数异常的风险计算
异常工况产生的风险包括固有风险和趋势风险。固有风险是状态参数偏离过程中已经产生的风险,其后果严重程度为损失函数的值,即后果严重程度为L,异常工况发生概率P=1,故根据风险计算公式,固有风险R1为:
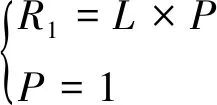
(8)
趋势风险用来表达由于参数仍具有向异常情况偏离的趋势所带来的风险,因损失函数的最大值为1,故异常状况的最大后果值为1,则参数偏离的最大后果严重程度为I=1-L,根据式(7)可以得到异常状况的发生概率P,故根据风险计算公式,参数的趋势风险R2为:

(9)
根据参数固有风险和趋势风险的计算公式,可以得到发生异常状况的风险:
R=R1+R2
(10)
因此,根据以上方法,可以将装置监控系统实时状态信息转换为风险信息,实现实时风险评估。
2 风险预警方法实施步骤
风险预警方法的具体实施步骤如下:
(1)采集一个工作时段(约8 h)内的状态参数值共5000组,存为数值矩阵B1×5000,该组数据的平均值记为M,参数的报警阈值为ylim,联锁报警阈值为Q。
(2)将Q作为造成最大损失的状态参数值,M作为状态参数目标值,则根据式(1),令T=M, Δ=Q-M, 公式变形如下:
(11)
(3)设置风险阈值:根据ALARP原则和帕累托分布的分级策略,将风险不可接受值到最大风险值之间的区域认定为不可接受的高风险区域,占总风险范围的20%[15]。因此,将风险不可接受值设置为风险报警阈值,得到风险阈值S为0.80。
(4)当状态参数y达到联锁报警阈值Q, 即y=Q时,损失函数达到最大值,即L=1; 当y与目标值M相同,即y=M时,装置处在最稳定状态,损失值为0,故L=0。 已知发生异常状况的风险参数包括固有风险R1和趋势风险R2, 当y达到报警阈值ylim, 且趋势风险R2=0时,为防止漏报,风险值应大于等于风险阈值,即R1≥0.8; 当y未达到报警阈值ylim, 且趋势风险R2=0时,为防止误报,风险值应小于等于风险阈值,即R1≤0.8; 推理可得,当y=ylim时,R1=0.8, 又根据式(8),R1=L, 故此时L=0.8, 即当y=ylim时,损失函数L=0.8。
根据以上分析,对于某些特定状态参数值yi, 其理想损失值Li已知(例:当yi=Q时,根据前文,L=1, 事实上,在实际运用过程中,可以根据实际情况增加损失函数的特征点,提高损失函数的匹配度,笔者只针对通用的3个特征点进行计算);又对于给定状态参数值y=yi和形状因子γ=γr, 运用式(11)可以计算出其实际损失值Lf。 因此,根据式(12)构造最小二乘方程组,求出使得偏差δ平方和最小的形状因子γ, 从而得出最接近理想状态的损失函数。
(12)
(5)计算参数所能引起的最大变化值:由于石油化工装置参数波动明显,运用最小二乘方法对数据集B1×5000进行拟合,并对拟合曲线进行一阶微分计算,得到参数历史数据的瞬时变化速率ΔVj。则得到最大允许变化速率ΔVt=max(ΔVj)。
(6)实时记录状态参数值y,将y带入式(11),得到参数的损失值为L,则根据式(8),可以得到固有风险值R1=L×P, 其中P=1。

(8) 根据式(10),可以计算装置的实时风险值R=R1+R2:
因状态参数变化趋势具有双向性,仅当状态参数变化方向与偏离目标值方向相同,即ΔVi与(y-M)同号时,才将趋势风险R2纳入整体风险的计算。
根据计算出的风险值,结合风险阈值,就可以实现实时风险评估。
3 案例分析
笔者将超早期精确预警方法分别应用到石油化工企业聚丙烯装置与气分装置的风险预警中,对该方法的有效性进行验证。
3.1 气分装置风险预警
3.1.1 工艺介绍
气分装置的主要作用是利用气体中各组分挥发度不同,对混合气体进行分离,该装置主要包含脱硫部分、脱硫醇部分和气体分馏部分,其主要任务是通过精馏使混合液态烃得到分离,从而生产出高纯度的丙烯以及其余部分,其中丙烯主要作为聚丙烯生产的原料,其余部分则成为液化气或其他化工生产原料。
现场软件通过DCS系统采集数据,并与预先设置的报警阈值进行比较,当参数超过报警阈值时则产生报警,图1为现场DCS系统监测图。当报警发生时,留给现场操作人员的相应时间较短,需要采用合适的预警方法实现装置的早期预警。

图1 DCS系统监测图Fig.1 Monitoring chart of DCS system
3.1.2 脱乙烷塔塔底液位风险预警
图2为气分装置脱乙烷塔塔底液位变化曲线,其报警阈值ylim=54.5%、报警联锁阈值Q=57%,状态参数历史数据平均值M=50%,实时状态参数值为y,因此,根据式(11),构造损失函数如下:
通过最小二乘法确定γ=3.024,将y带入构造出的损失函数,计算出实时的损失值L,则根据式(8),可以求得参数固有风险值R1=L×P,其中P=1。

状态参数实时风险值R为:
R=R1+R2
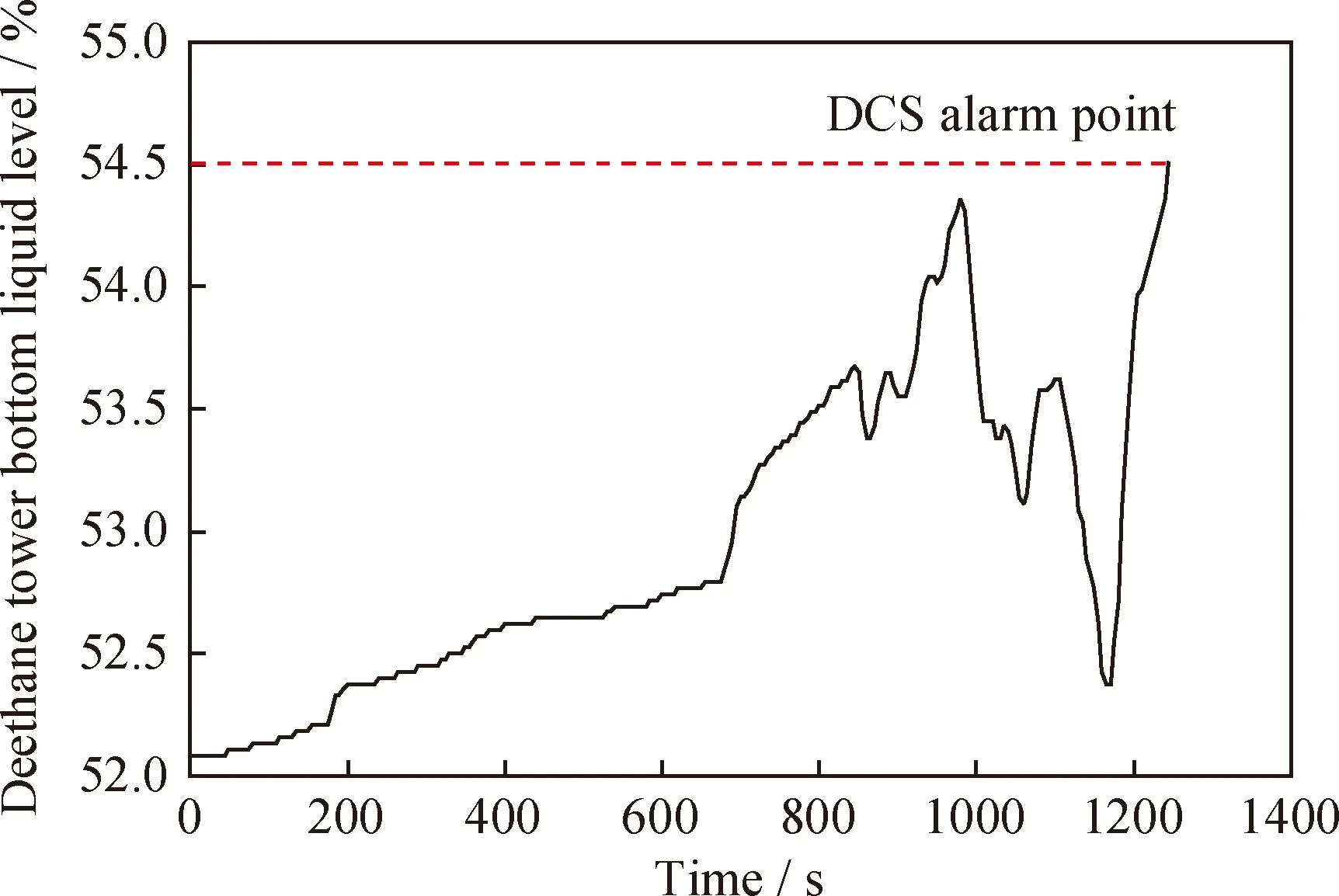
图2 脱乙烷塔塔底液位变化曲线Fig.2 Profile of deethane tower bottom liquid level
绘制装置的实时风险曲线如图3所示。

图3 脱乙烷塔塔底液位风险曲线Fig.3 Risk profile of of deethane tower bottom liquid level
可以看出,风险值在695 s开始超出报警阈值,发出预警,于900 s左右快速上升并反复超出报警限。由图3可知,该参数在1250 s时达到报警阈值触发DCS报警。结果表明,该方法较DCS报警提前10 min左右。
3.1.3 脱乙烷塔塔顶压力风险预警
选择脱乙烷塔塔顶压力作为目标参数,其参数变化曲线如图4所示,报警阈值ylim=2.773 MPa,报警联锁阈值Q=2.785 MPa,历史数据平均值M=2.75 MPa,实时状态参数值为y,根据式(11),构造损失函数如下:
通过最小二乘法确定γ=0.0133,将y带入构造出的损失函数,计算出实时的损失值L,则根据式(8),固有风险值R1=L×P, 其中P=1。

状态参数实时风险值R为:
R=R1+R2
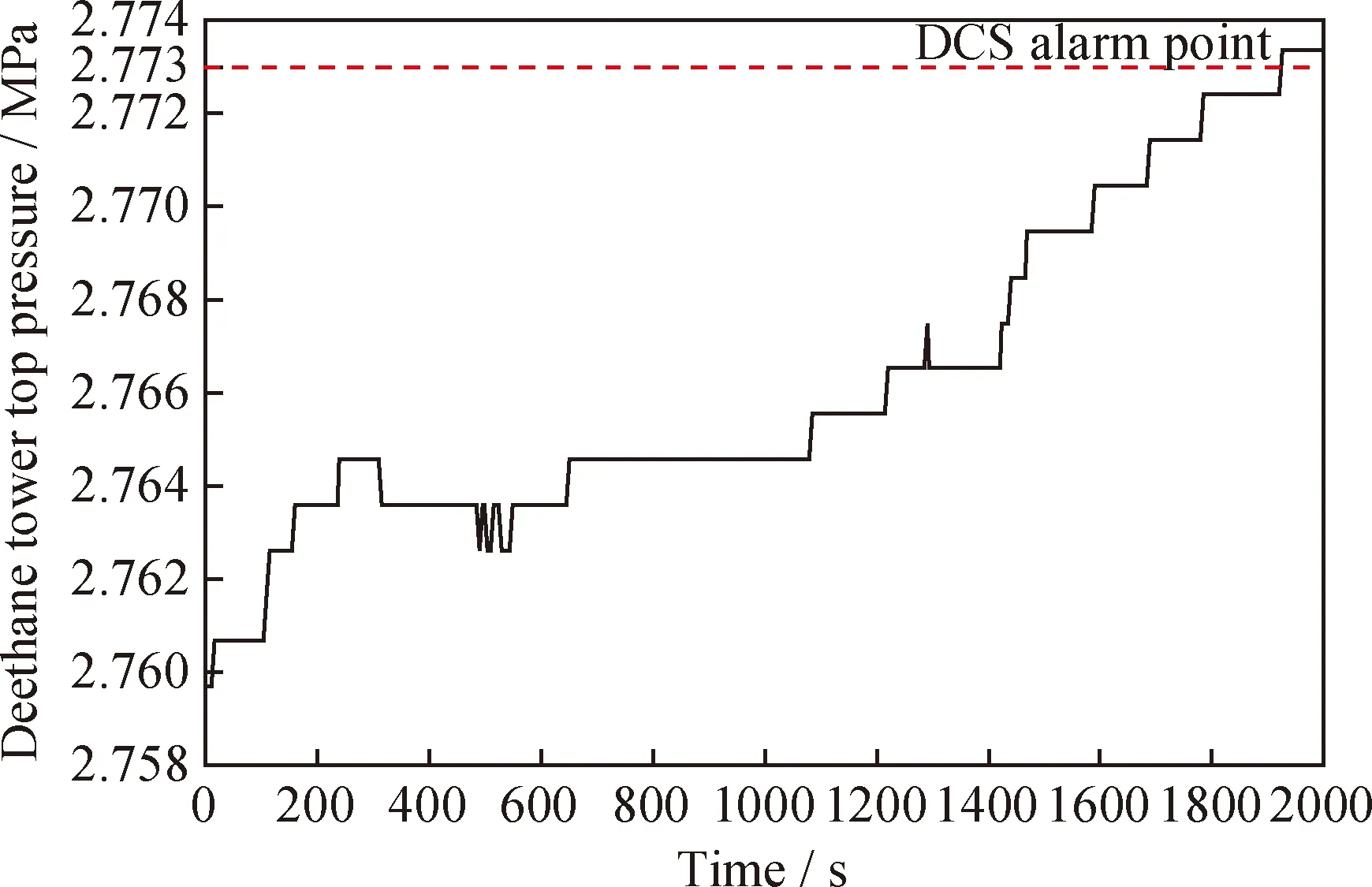
图4 脱乙烷塔塔顶压力变化曲线Fig.4 Profile of deethane tower top pressure
绘制装置的风险曲线如图5所示。

图5 脱乙烷塔塔顶压力风险曲线Fig.5 Profile of deethane tower top pressure
由图5可得,风险曲线1470 s左右达到风险阈值,发出预警。由图4知,状态参数于1995 s产生DCS报警。结果表明,该方法较DCS报警提前8 min 左右。
3.2 聚丙烯装置风险预警
3.2.1 聚丙烯装置介绍
聚丙烯装置是利用气分装置产出的丙烯气生产聚丙烯产品的装置系统,该装置主要包含丙烯精制系统和聚合闪蒸系统,其中丙烯精制系统令原料丙烯通过各精制塔,通过各物理或化学作用,脱去其中的硫、水、氧、砷等杂质,为下一道聚合工序储备原料。聚合闪蒸系统通过向聚合釜中投入催化剂、活化剂、二苯基甲基二甲氧基硅烷(DDS)、氢气等助剂,用热水升温激活反应,从而生成聚丙烯,并回收未反应的丙烯至回收计量罐。聚丙烯装置通过将DCS系统对现场异常状况进行监控,如图6所示,笔者通过风险预警方法对聚丙烯装置进行预警。

图6 聚丙烯装置DCS监测图Fig.6 Parameter alarms of polypropylene devices
3.2.2 热水罐液位风险预警
选择聚丙烯装置热水罐液位作为待测参数,其参数变化曲线如图7所示,其报警阈值ylim=82%、报警联锁阈值Q=95%,历史数据平均值M=60%,实时状态参数值为y,因此,根据式(11),构造损失函数如下:
通过最小二乘法确定γ=12.58,将y带入构造出的损失函数,计算出实时的损失值L,则根据式(8),固有风险值R1=L×P,其中P=1。
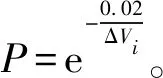
状态参数实时风险值R为:
R=R1+R2
绘制装置的风险图如图8所示。
由图8可知,在1185 s时状态参数风险值超标,此时DCS系统尚未达到报警阈值。这是由于参数上升速率过快,导致趋势风险增大所引起的。1225 s 时参数风险值再次超标并在阈值附近波动。由图7得,参数于 2170 s 时超过DCS报警阈值并发出报警。结果表明,该方法较DCS报警提前16 min 左右。

图7 热水罐液位变化曲线Fig.7 Profile of hot-water cylinder liquid level
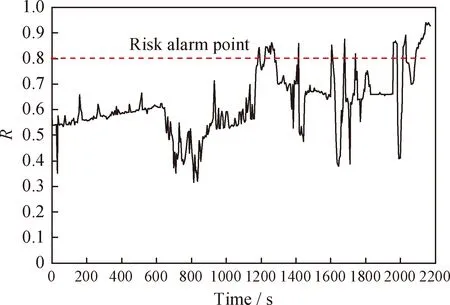
图8 热水罐液位风险曲线Fig.8 Risk profile of hot-water cylinder liquid level
根据该方法应用于不同状态参数的风险预警情况,将预警结果整理如下:

表1 不同状态参数预警时间Table 1 Early warning time of different parameters
事实证明,该方法可以放大参数的早期偏差,实现参数的早期预警,根据案例分析,该方法对于不同的异常均能很好地检出,并在参数到达报警阈值前10 min左右发出预警信息,对异常工况进行有效预警。
4 结 论
(1)针对石油化工装置现有的预警技术误报率较高,以及风险预警方法无法定量分析等不足,将损失函数应用到石油化工装置的风险预警中,通过构造合适的损失函数,定量描述参数偏离所产生的预期损失,并根据剩余时间理论计算化工过程异常工况发生的概率,定量计算出参数偏离所产生的风险,从而实现异常工况的风险预警。
(2)将该方法分别应用到石油化工企业的聚丙烯装置与气分装置的风险预警,通过计算相关参数的风险值,并与实际情况进行比对,从而对方法效果进行验证。
(3)结果表明,随着监测参数接近报警限,装置风险值明显上升,且参数变化幅度越大,该风险值上升越快。这说明该风险预警模型能有效地将状态参数的偏离和参数的变化趋势转化为实时的风险信息,对非合理状态参数变化趋势进行风险预警。该方法用于状态参数发生偏离的初期辨识,可以提前10 min左右监测到异常,对异常工况进行有效预警。
