适用于并网系统的长距离传输电缆建模研究

赵世坡，王海宝，赵世超，张 婧，李波涛，崔朋玉，孙孝峰,*

(1.国网冀北电力有限公司张家口供电公司，河北 张家口 075000；2.北京智芯微电子科技有限公司，北京 100192；3.燕山大学 电气工程学院，河北 秦皇岛 066004)

0 引言

随着新能源发电技术的迅速发展，电力电子变流器在基于可再生能源的分布式发电中发挥了重要作用[1]。一般而言，电流控制方式的逆变器可以通过大型风电场或光伏形式的长传输电缆与电网连接。以现代风力发电机组为例，它通常采用背靠背逆变器通过高压交流或高压直流传输电缆进行并网连接[2]。在实践中，一组风力发电机通过电压源型逆变器、升压变压器和高压交流海底电缆连接到陆上公共连接点。典型并网风力发电系统的等效电路如图1所示[3]。

图1 风力发电并网系统
Fig.1 Wind power grid-connected system

新能源并网系统的分析和设计通常涉及输电线路的特点。文献[4]提出了谐波不稳定现象，并提出了抑制LCL滤波器谐振的解决方案。文献[5]分析了谐波对电力电缆损耗的影响。在一个光伏电站中，分析了带LCL滤波器的n台逆变器并联并网逆变器的建模以及传输线等效阻抗的耦合效应[6]。在这些研究中，并网系统中的短传输线通过忽略寄生电容的影响而相当于纯电感。

然而，较长的传输线由于分布电容较大，电压、电流的谐振现象可能发生在长传输线上。此时，在传输线末端安装的阻性有源滤波器可实现谐波抑制。考虑到寄生电容，采用长传输线的分布式集总参数模型来研究谐波传播问题。文献[7]针对背景谐波抑制问题，详细研究了等效阻抗的推导并提出背景谐波放大现象的解决方案。文献[8-9]通过在传输线末端设置特征阻抗，基于谐波传播原理提出了实际传输线的等效阻抗模型，并分析了通过长距离传输线连接到电网的海上风电场系统的稳定性问题。

但由于长距离传输电缆的实际阻抗模型是一个超越函数，在分析含有传输线系统时的特征方程就会含有超越项，想要直接求解方程从而得到系统的特征值就变得很复杂。本文提出了一种适用于并网系统分析的长输电线路线性模型。基于分布参数模型，采用Taylor线性化拟合对长传输线路等效阻抗模型进行线性化，并对拟合阶数进行分析，对传输线阻抗模型以及拟合的本质进行了讨论。提供了完整的长距离传输电缆最优拟合阶数选择方法。

1 线性化方法

1.1 系统模型

图2是单相高压交流电缆原理图。假设配电线路上的电阻、电感和电容均匀分布，线路空载、无支路，且其中Vin和Vg分别表示微电网和电网的等效电压源。线路参数如表1所示，该参数基于日本一个6.6 kV、3 MVA的实际传输线[10]。

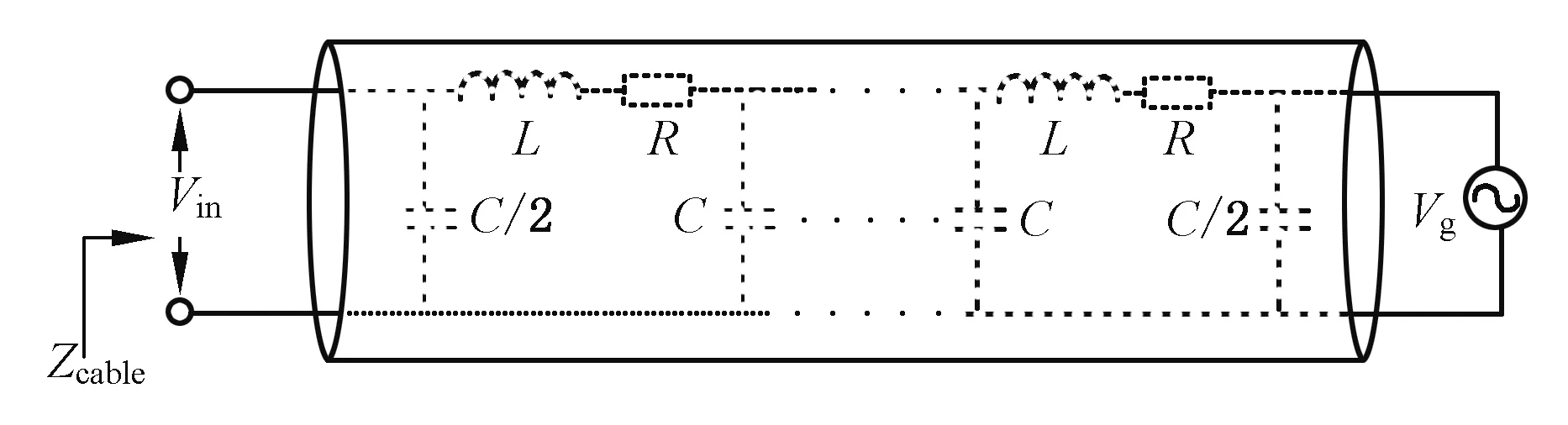
图2 传输电缆原理图
Fig.2 Schematic diagram of transmission cable

表1 线路参数
Tab.1 Circuit parameters

系统参数取值基波频率50 Hz线路电感L1.98 mH/km线路电容C25 μF/km线路电阻R0.5 Ω/km

如表1中的L、C、R为传输线的原参数，而特征阻抗Z0和传播常数γ为传输线的复参数[11]。复参数会随着传输线即原参数的确定而确定，而复参数是研究传输线问题的基本参数。

特征阻抗为

(1)

传播常数为

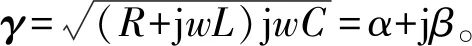
(2)

图3为从逆变器侧看向电网而建立的等效传输电缆的集总参数和分布参数模型。根据叠加定理，电网等效为理想电压源，在谐波频率下表现为短路特性。l为传输电缆的长度，R、L、C为表1所示的线路参数，根据传输线理论[12]，得到等效阻抗Zcable表达式为

Zcable=Z0tanh(γl),

(3)

Z0为传输电缆的特征阻抗，l表示传输电缆长度，Zcable为逆变器侧向电网侧看的传输线等效阻抗即电网等效阻抗。

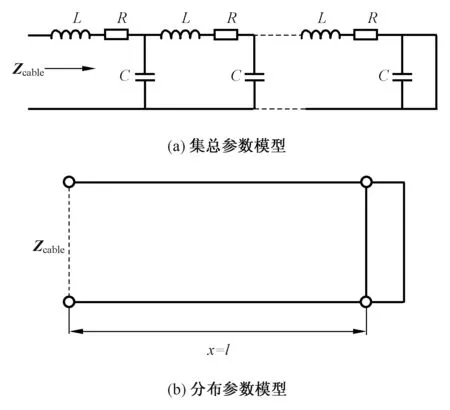
图3 传输电缆参数模型
Fig.3 Parameter model of the transmission cable

1.2 Taylor近似

由式(3)可以看出末端短路的传输电缆等效阻抗是一个双曲函数。分析含有长传输电缆模型的系统时，会使该系统的特征方程含有超越项，导致求取系统的特征值变得很困难。所以需要对传输电缆模型进行线性化。对式(3)进行进一步整理得

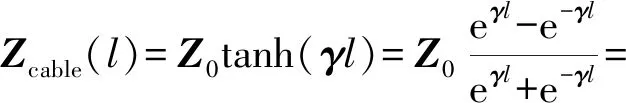
(4)

式中仅含有指数项e-2γl，则对传输电缆模型的线性化问题转化为对指数项e-2γl的线性化问题。

本文通过Taylor级数展开的方法对指数项进行线性化。

Taylor级数展开根据n阶有理多项式逼近ex：

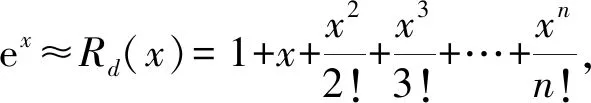
(5)

式中，n的阶数越大，Rd(x)越接近ex。用Taylor级数展开对ex进行阶数为一和二的线性化拟合后带入式(4)中，结果为

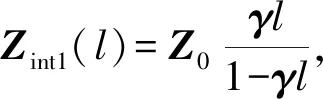
(6)

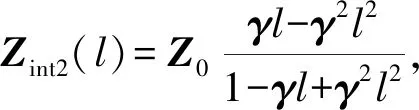
(7)

Zint1(x)的截断误差是O(h2)，是一阶精度；Zint2(x)的截断误差是O(h3)，是二阶精度，h为仿真步长。

在阶数不同时，经过计算可知当拟合阶数为n(n≥1)时，得到的线性化模型精度同样为n阶。

2 传输电缆线性化模型

在分析传输电缆长度与拟合阶数之间的联系之前，首先要明确研究的频率范围。传输电缆的谐波源主要是上级电网渗透的背景谐波，同时用户侧或分布式发电单元在高频段的谐波含量很小，所以本文以50～1 000 Hz为例进行拟合阶数的分析。如果研究的频率范围与1 000 Hz不同，可以利用本文方法重新进行阶数选择。

2.1 实际阻抗模型

为了分析不同拟合阶数下Taylor级数模型与实际模型的吻合度。该文使用MATLAB对频率进行逐个描点绘制得出了传输电缆阻抗的实际模型，并且对传输电缆实际模型的等效阻抗伯德图的特征进行分析。

图4是依据式(3)绘制的线性化前的传输线实际阻抗模型。图中传输电缆等效阻抗伯德图每隔一段频率会出现一个谐振尖峰。通过相频特性看出传输电缆等效阻抗随着频率的增加呈阻感性和阻容性周期性变化。谐振峰有无穷多个且增益不会衰减。由于系统中高频的谐波源含量很低，所以真实模型中出现在高频段的谐振峰不仅没有意义,还会增加分析系统的难度。对实际模型选取适当的拟合阶数可以在去除高频段谐振峰的同时保证研究频段内传输电缆阻抗模型的特征不变。

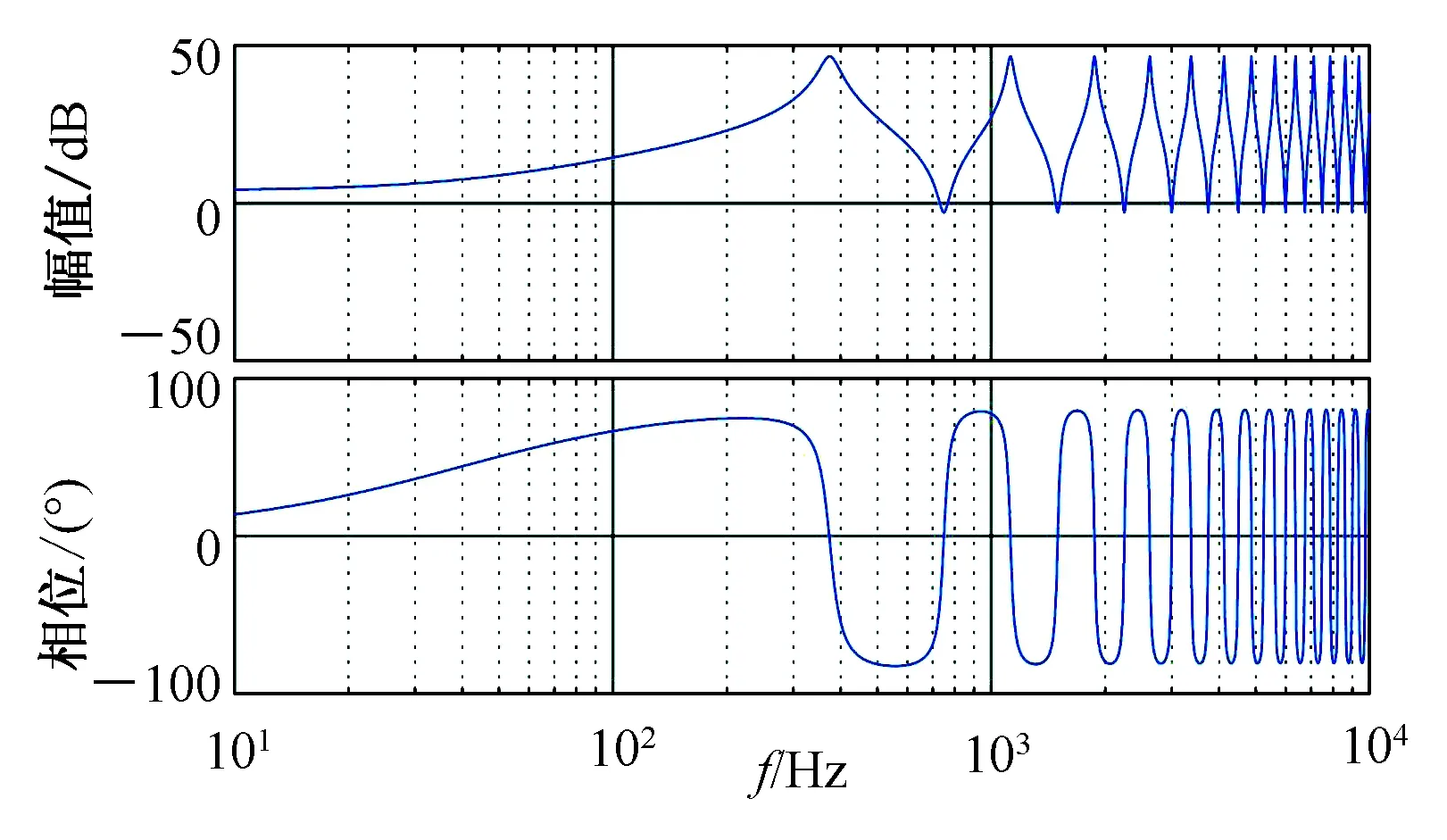
图4 传输电缆实际等效阻抗伯德图
Fig.4 Actual equivalent impedance Bode diagram of the transmission cable

2.2 传输电缆长度与拟合阶数

由式(3)可知，随着传输电缆参数γ和Z0的确定，和输出阻抗直接相关的只有传输电缆的长度l。本节分析传输电缆长度和Taylor近似阶数之间的关系。

1) 传输电缆长度l=0.1 km

由图5可以看出当传输电缆长度为0.1 km时，Taylor一阶拟合模型与实际模型在50～1 000 Hz频率范围内重合。所以在此长度下，实际模型可以有理近似为一阶模型，即

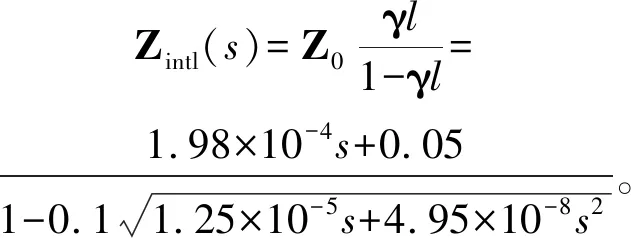
(8)

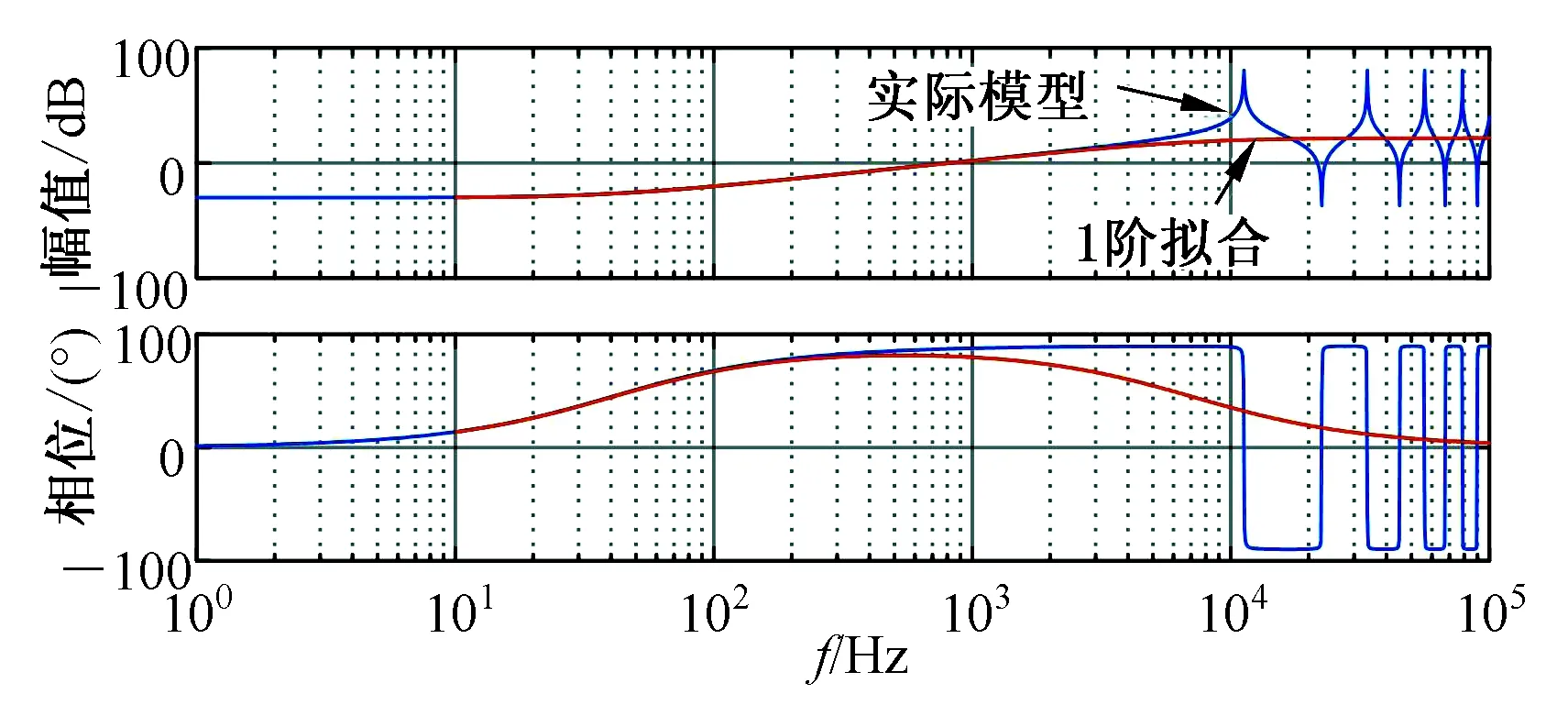
图5 0.1 km传输电缆模型
Fig.5 0.1 km transmission cable model

2) 传输电缆长度l=1 km

由图6看出当传输电缆为1 km时，一阶拟合模型在300 Hz左右就和实际模型的重合度变差，不满足研究范围内的精度要求。因此为了提高精度，当拟合阶数增加到五阶时，拟合模型和实际模型仅能在800 Hz范围内重合。当阶数增加到7阶，拟合模型和实际模型可以在1 000 Hz范围内完全重合。所以，当传输电缆长度为1 km时，实际模型可以有理近似为7阶模型。

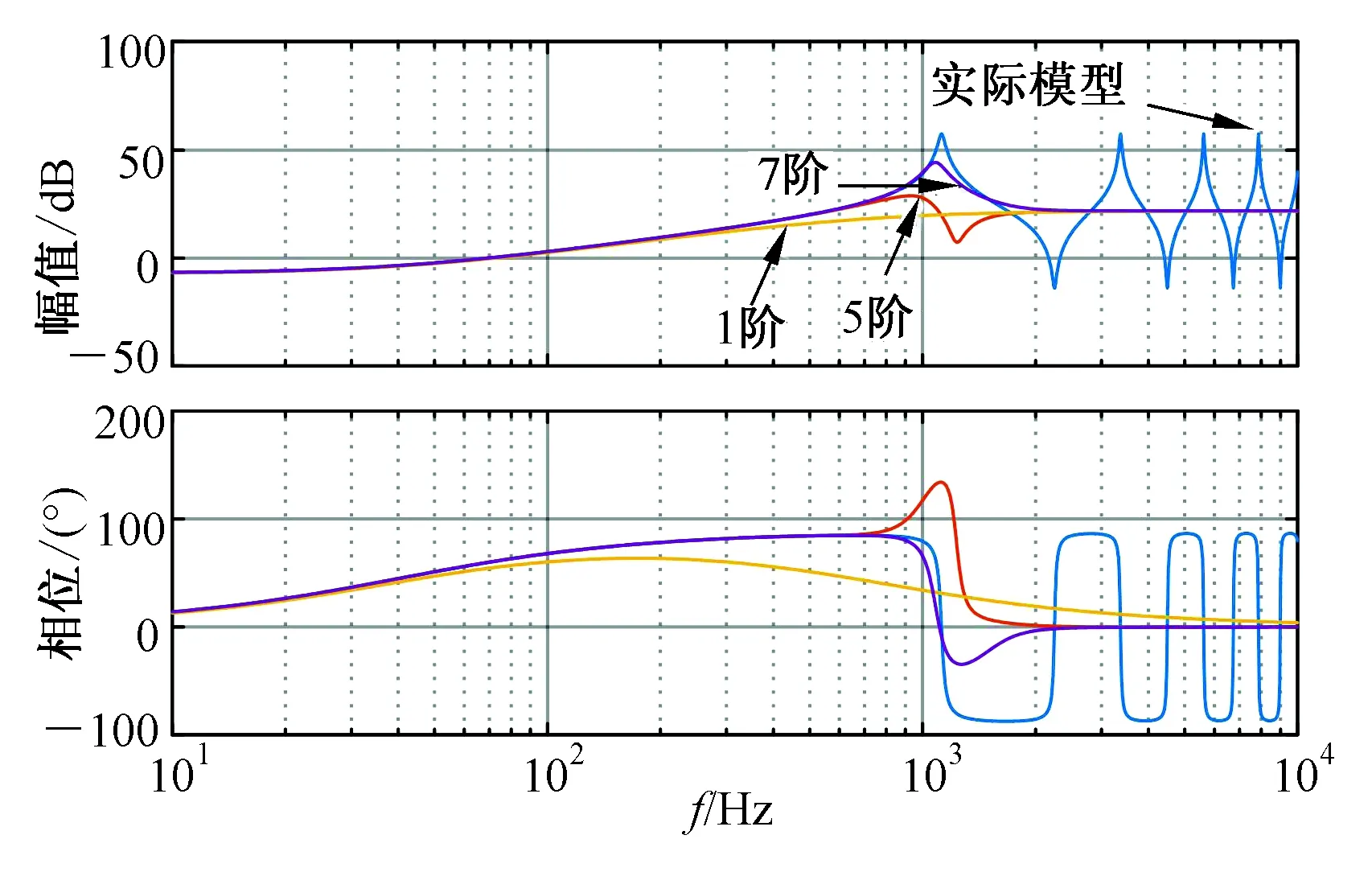
图6 1 km传输电缆模型
Fig.6 1 km transmission cable model

3) 传输电缆长度l=3 km

从图7看出，当传输电缆增长为3 km时，5阶拟合和7阶拟合模型在50～1 000 Hz频段内和实际模型的误差越来越大。所以相对于0.1 km和1 km传输电缆，长距离传输电缆需要高阶拟合模型。

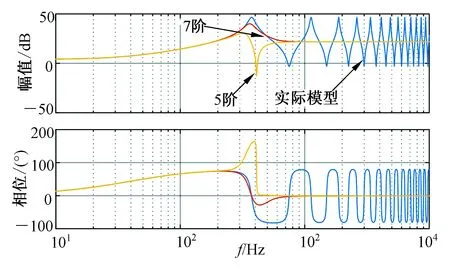
图7 3 km传输电缆模型
Fig.7 3 km transmission cable model

3 长距离传输电缆拟合阶数

由2.2节可知短距离传输线选择低阶拟合模型即可，长距离传输电缆则要选择精度更高的高阶拟合。所以拟合阶数的选取成为传输线线性化的主要问题。

3.1 选择依据

本节给出选择阶数时依据的原则以及遵循的思路：1)低阶原则，选择阶次要尽可能低，以利于简化系统分析从而减少工作量；2)特征匹配，确定合适的传递函数的阻抗是否匹配，需要对不同阶数下伯德图进行比较，总结变化规律。这需要在确定传输电缆长度的前提下，可以得到确定的传输电缆传递函数，把传输电缆长度看成固定量，阶数看成自变量，研究不同阶数下的传递函数Bode图，与实际模型进行比较，从而确定最优拟合。下面对3 km传输电缆拟合阶数的选择过程做详细的介绍。

使用Taylor级数展开，观察不同拟合阶数d下，传输电缆等效阻抗的Bode图，取l=3 km，如图8所示。

图8(a)为1、3、7阶拟合模型，1阶模型并没有谐振峰，3阶和7阶模型开始出现谐振峰，且结合图8(b)中的9、13、14阶模型可以看出随着拟合阶数的增加，谐振峰个数在逐渐增加。且从13阶以及14阶模型看出，谐振峰的峰值也逐渐升高。再结合图8(b)、(c)可以看出高阶拟合模型在低频段的等效阻抗模型特征不会发生改变。高阶模型之间低频段Bode图重合的频段越来越宽。

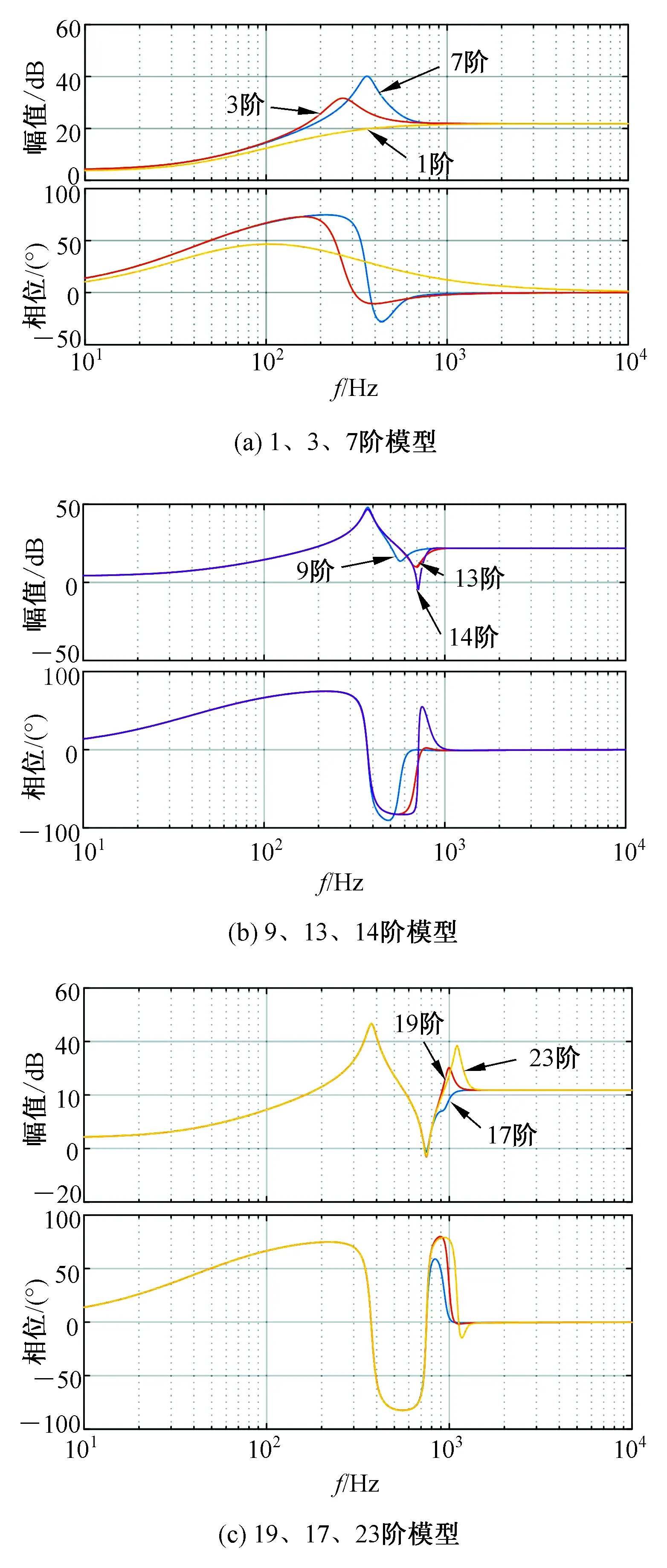
图8 不同拟合阶数下传输电缆等效阻抗Bode图
Fig.8 The equivalent impedance Bode diagram of transmission cable derived with different orders

所以，Taylor拟合模型规律如下：1)传输电缆拟合阶数变大时，对应的低频段Bode图并没有发生较大变化，且随着拟合阶数的增高，低频段重合的增益频段变宽。2)随着拟合阶数增加，阶数越高谐振峰的峰值或者个数或逐渐升高或增加，越接近实际模型的等效阻抗Bode图。

在图9中，随着拟合阶数的增加，在50～1 000 Hz频率范围内，经Taylor拟合得到的线性化模型和实际模型匹配程度越来越高。在图9(a)，14、17阶拟合模型都不能在研究频率范围内和实际模型完全匹配。根据特征匹配原则需要进一步提高拟合阶数来提高匹配度。图9(b)中19阶和23阶拟合模型都可以在研究频率范围和实际模型完全匹配。考虑低阶原则，最终得出结论，当传输电缆为3 km时，19阶拟合为最优拟合。

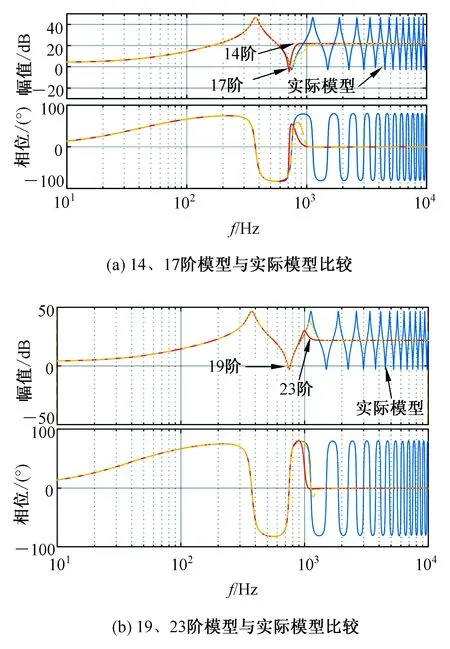
图9 高阶Pade拟合与传输电缆实际模型
Fig.9 The high order Pade fitting model and the actual module of transmission cable

3.2 仿真验证

3.2.1实际模型仿真验证

在2.1节中对传输线实际模型的特征进行了分析。为了验证建立模型的真实性，本节通过MATLAB/simulink软件中的分布参数模块与传输线的实际模型进行了比较，其中分布参数模块参数设置如表2所示。图10可以看出，分布参数仿真模块和实际模型的等效阻抗完全重合，验证了传输线实际阻抗模型的可靠性。

表2 分布参数模块
Tab.2 Distributed parameter module

参数取值段数3每段传输线长度/km1线路电感L/mH1.98线路电容C/μF25线路电阻R/Ω0.5

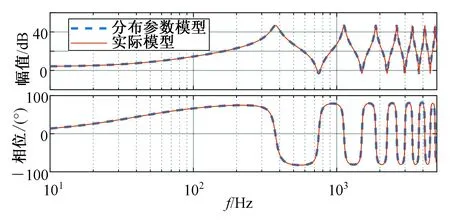
图10 传输线实际模型和分布参数仿真模型
Fig.10 The actual module of transmission cable and distributed parameter simulation module

3.2.2Taylor拟合模型仿真验证

在仿真或者实验中通常使用π型电路级联的模型来等效长距离传输电缆。如同Taylor拟合模型与实际模型之间的关系，仿真模块中π型电路模型是分布参数模型的线性化模型。以1段π形电路代表1 km长度、3 km的传输电缆可等效为3段π形电路级联模型。

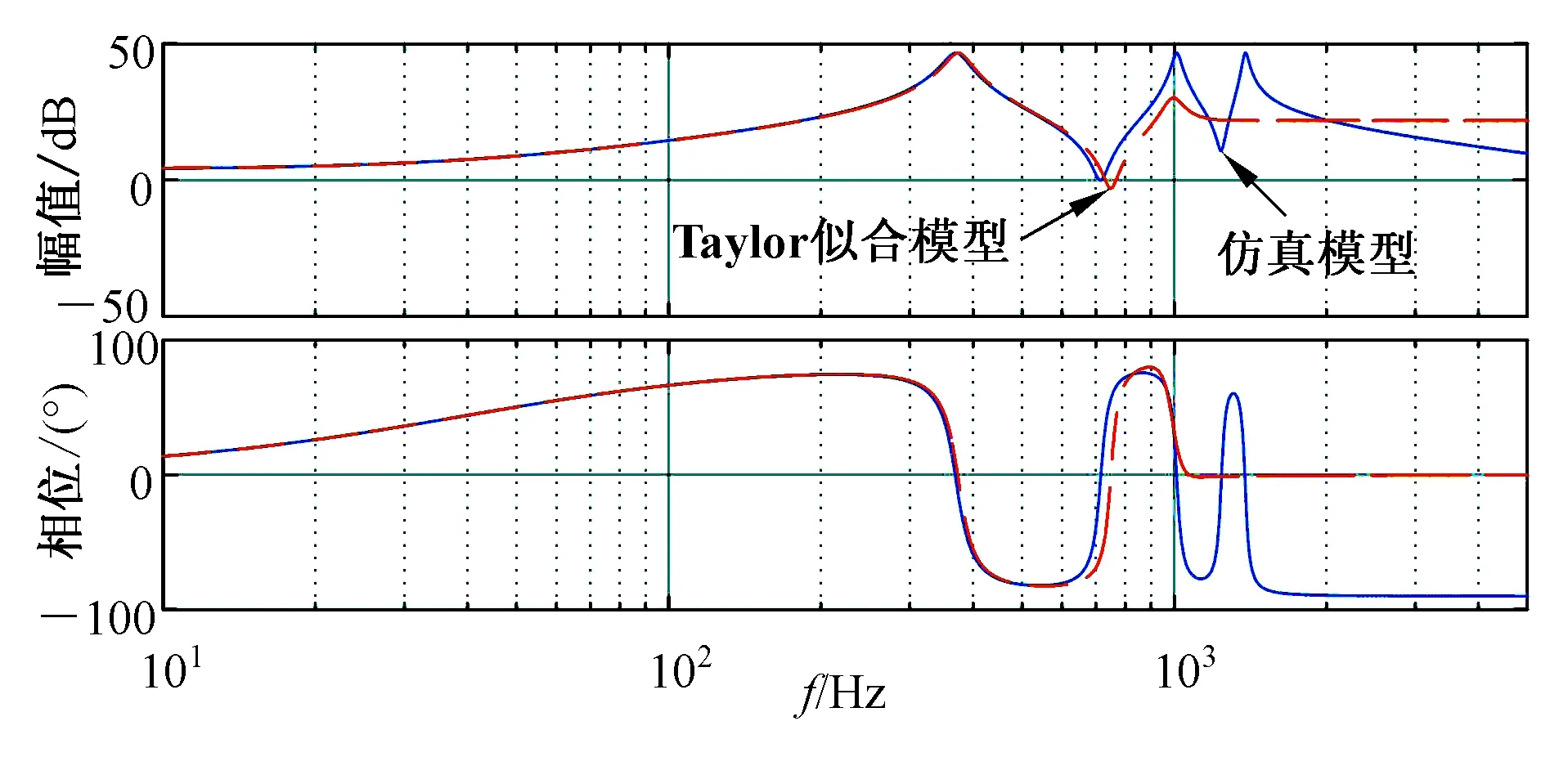
图11 Taylor拟合模型和仿真模型
Fig.11 Taylor linearized model and simulation model

从图11中可以看出Taylor拟合模型和π型电路仿真模型在1 000 Hz的频率范围内的阻抗是重合的，验证了Tylor拟合模型的正确性。

3.3 实验验证

为了验证拟合阶数的正确性，本文使用FRA5097频谱特性分析仪对当长度为3 km的传输电缆模型进行了实验验证。所得到的传输电缆等效阻抗幅值特性如图12所示。

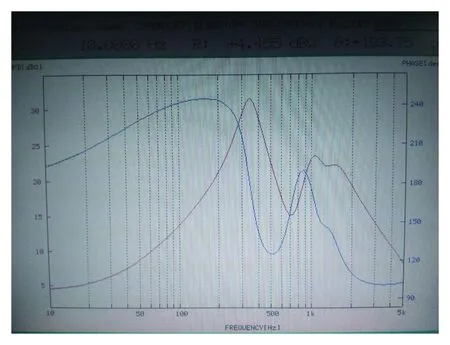
图12 传输电缆等效阻抗频率响应
Fig.12 Frequency response of the equivalent impedance of transmission cable

图12中可以明显看出在低频段，传输电缆等效阻抗在350 Hz、700 Hz、1 000 Hz出现3个谐振峰。图12和图9中经Taylor拟合的等效阻抗走势一致，证明传输电缆等效阻抗所拟合的19阶模型在50～1 000 Hz频段的正确性。

4 结论

长传输线的分布电容参数较大，易与线路分布电感引起谐振，因此在进行传输线模型特性研究时分布电容不可忽略。本文通过考虑传输电缆的分布电容、分布电阻，给出了长传输电缆的实际阻抗模型并对其进行线性化，介绍了Taylor拟合线性化方法的精度，并给出了Taylor拟合阶数选择的依据。以3 km传输线为例，建立了19阶Taylor线性化模型，保证了该模型在50～1 000 Hz范围内的精确性。最后通过仿真和实验验证了线性化方法的可行性和准确性。