RBF神经网络在曲面缺陷修复与重构中的应用研究

■林丽萍

(福建船政交通职业学院，福州 350007)

1 引言

在市场朝着多品种、小批量、个性化方向发展的趋势下，逆向工程因其能够大幅降低产品生产周期、提高生产效率得到广泛应用[1，2]。逆向工程从实物样件出发，采用现代测量技术获取样件数字信息，通过曲面重构技术在计算机中构造样件实体模型，进而利用先进加工技术制造样件实体。实施逆向工程的关键技术包括数据采集、数据处理、曲面重构、曲面检验和修正、CAD模型构造等。曲面重构实现对样件点云数据的网格划分、特征提取、表面分片和曲面生成等，是逆向工程的核心环节。曲面重构的数据来源是经过数据处理的点云数据。当样件形状结构较为复杂时，表面模型主要是自由曲面，难以直接用解析的方法描述。此外，在测量过程中，由于采集的点云数据可能存在精度误差及噪声，甚至因为样件表面残缺造成信息缺失，需要对样件表面模型进行缺陷修复。

为降低曲面修复操作复杂度，提高曲面修复效率与曲面重构精度，国内外许多学者对曲面修复与重构进行了研究，取得了一些效果，但依然存在许多不足，主要表现在：(1)针对复杂样件表面难以初等解析曲面进行表达等问题，部分学者提出用参数曲面进行描述，进而修复缺陷实现曲面重构的方法[3，4，5]，实现了曲面的显示描述，但存在建模难度大、适用性范围窄等问题；(2)部分学者提出基于隐式函数的曲面描述方法，具有解析式明确，便于使用微积分等数学工具的优点，有效实现曲面缺陷修复和重构[6，7]，但存在约束条件复杂，描述效率低，求解过程复杂等问题，且对采样点的分布要求较高，容易出现过拟合导致缺陷修复失败；(3)针对显示描述和隐式描述存在的建模难度大的问题，部分学者提出了三角化逼近描述曲面的方法，并基于三角网格模型实现了曲面缺陷修复和曲面重构[8，9]，具有构造灵活，对曲面边界的适应性好，适用于科学计算等优点，但同时存在局部编辑困难、精度不够时曲面易出现明显棱角等缺陷；(4)为降低建模复杂度，提高缺陷修复和曲面重构效率，部分学者提出了基于神经网络的曲面表示方法[10-12]，利用神经网络的强非线性映射能力拟合曲面，进而通过模型预测实现缺陷修复和曲面重构，具有计算效率高，适用范围广等优点，但存在神经网络建模参数的选择受人为因素影响较大，重构的曲面光滑性难以保证等不足。将神经网络与曲面插值相结合，利用神经网络的强非线性映射能力实现曲面拟合，通过神经网络的预测实现曲面缺陷修复，进而采用曲面插值实现光滑曲面的重构，能够有效降低曲面建模难度，提高曲面缺陷修复精度和重构效率。RBF神经网络是三层前馈型神经网络，能够以任意精度逼近任何连续函数，适用范围广，且具有训练速度快，不易陷入局部极小等优点。三次插值不仅能够保证生成的曲面二阶连续，而且具有算法简单，易于实施，计算效率高等优点。

综合上述分析，探讨基于RBF神经网络和三次插值的曲面缺陷修复与重构策略，利用RBF神经网络实现曲面拟合和缺陷修复，通过三次插值实现曲面重构，具有重要理论与现实意义。

2 曲面缺陷修复工作机制

针对现有曲面缺陷修复与重构中存在的受人为因素影响大、建模难度大、约束条件复杂、修复精度低、重构效率低下的问题，采用基于RBF神经网络实现曲面拟合与缺陷修复，基于三次插值实现曲面重构的策略，工作机制如图1所示，具体工作流程如下：

(1)确定待分析数据集。通过接触式或非接触式测量等方式对样件进行数据采集，获取样件表面点云数据，并对点云数据进行多视拼合、降噪处理、缺陷数据删除等操作，进而获得取值合理的待分析数据集S，如下式所示：

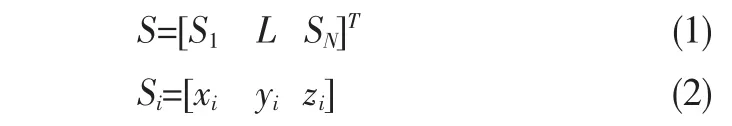
其中，N为待分析数据集的容量，Si为第i(i=1～N)个待分析数据，由点云数据中各点坐标值(xi，yi，zi)构成。

(2)RBF神经网络建模。基于待分析数据集S，以定义域(xi，yi)作为输入神经元，zi作为输出神经元，进行 RBF神经网络建模，利用RBF神经网络的强非线性拟合能力对曲面进行拟合，构建zi关于(xi，yi)的黑箱模型。

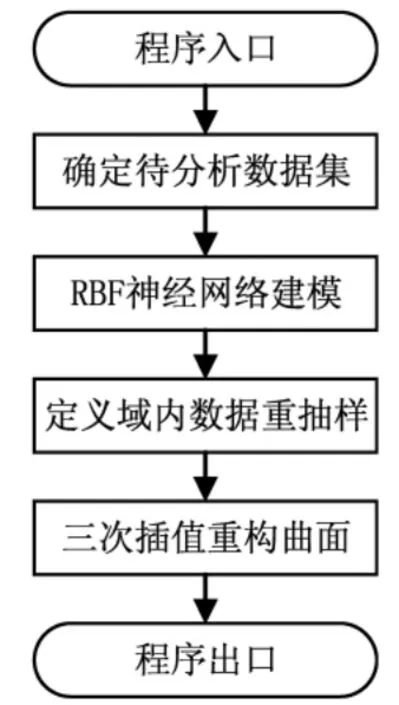
图1 曲面缺陷修复工作机制

(3)定义域内数据重抽样。在获得RBF神经网络的基础上，根据曲面重构精度要求在定义域内进行均布重抽样得到新的定义域I：

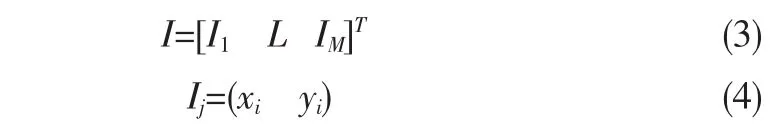
其中，M为重抽样后的数据集容量，IJ为定义域I的第j(j=1～M)个数据。当I确定以后，利用RBF神经网络的预测能力，可以得到与各个IJ对应的输出OJ，OJ即坐标IJ对应的Z坐标值，从而得到重抽样后的曲面数据点集R：

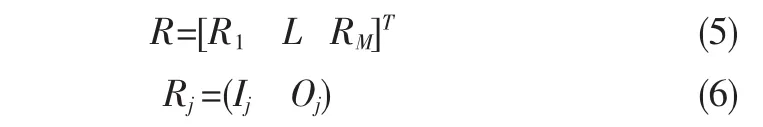
通过定义域均布重抽样，不仅可以通过定义域覆盖缺陷区和RBF神经网络预测实现缺陷修复，而且可以使曲面重构中的插值点均布在定义域内，有效降低插值误差，提高曲面重构精度。

(4)三次插值重构曲面。在获得重抽样后曲面数据点集R的基础上，利用三次插值，即可基于现有点集R重构曲面，且具有二阶连续、算法简单、易于实施、计算高效等优点。

RBF神经网络建模是基于RBF神经网络和三次插值的曲面缺陷修复与重构策略的核心，其预测精度决定了曲面重构精度。RBF神经网络为3层结构包括输入层、隐含层和输出层。其中，进行曲面拟合时，输入层的神经元个数为2个，分别对应X坐标值x和Y坐标值y，输出层的神经元个数为1个，即Z坐标值。用于曲面拟合的RBF神经网络结构如图2所示，其中隐含层神经元个数为P，径向基函数采用高斯函数。

图2 曲面缺陷修复工作机制

本文采用Matlab R2014b Toolbox中的newrb函数建立和训练RBF神经网络。该函数中，除训练样本集中的输入数据和输出数据外，主要的模型控制参数是分布参数s。为避免人为选择分布参数s带来的人为因素影响大的问题，采用如图3所示的RBF神经网络优化建模方法，具体流程如下：

(1)在确定输入样本和测试样本的基础上，设定分布参数s的上限su、下限 sd及搜索步长 Δs，并令 s=sd，索引变量i=1。

(2)根据教师样本训练第i个RBF神经网络Ni，根据测试样本计算Ni的平均预测误差Ei，并保存Ni和Ei。

(3)若 s＜su,则令 s=s+Δs，i=i+1，并转(2)；否则将|Ei|值最大时对应的Ni作为训练结果输出。

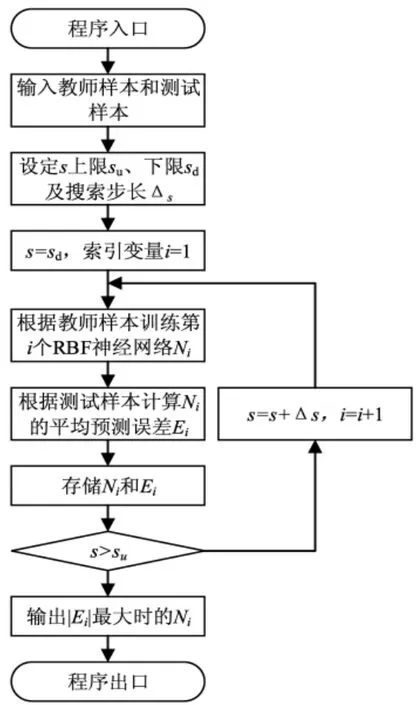
图3 RBF神经网络优化建模方法

3 实例

为验证所提基于RBF神经网络和三次插值的曲面缺陷修复与重构策略的可行性和有效性，以基于某给定曲面点云数据的曲面修复与重构为例，分别采用直接三次插值和本文所提策略进行曲面修复与重构性能分析。已知该给定曲面为椭圆抛物面，曲面方程如式7所示。

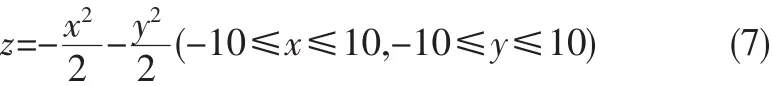
对该曲面进行抽样后得到曲面点云数据共200个，去掉-2≤x≤2范围内的数据点后剩余数据160，形成一个带缺陷的曲面点云，如图4所示。

图4 曲面缺陷修复工作机制

直接采用基于三次插值的方法进行曲面修复与重构结果如图5所示。重构后，该椭圆抛物面顶部较为扁平，与原椭圆抛物面形状差异较大，主要是因为曲面缺陷修复时，缺陷处的修复误差较大，变化范围为(-4，4)。

随机选择160个数据中的120个数据作为样本，剩下40个数据作为测试样本，构建RBF神经网络。取sd=0.1，su=10，目标精度 0.0001，经过寻优，当 s=4.1 时，RBF神经网络训练结果为最优，训练过程曲线如图6所示，经过100次迭代，网络收敛，隐含层神经元个数为P=100。基于训练好的神经网络对缺陷处的z值进行预测，实现缺陷的修复，进而采用三次插值重构椭圆抛物面，结果如图7所示。对比图5可知，基于RBF神经网络和三次插值的曲面修复与重构结果曲面更为光滑，且重构精度更高，误差变化范围为(-0.04，0.04)。

图6 RBF神经网络训练过程曲线

4 结论

曲面缺陷修复与曲面重构是逆向工程的核心环节。针对现有曲面缺陷修复与重构中存在的受人为因素影响大、建模难度大、约束条件复杂、修复精度低、重构效率低下的问题，开展基于RBF神经网络和三次插值的曲面缺陷修复与重构策略，具有重要理论与现实意义。通过探讨基于RBF神经网络实现曲面拟合与缺陷修复，基于三次插值实现曲面重构的策略，研究RBF神经网络的优化建模方法，以某椭圆抛物面的缺陷修复与重构为研究对象，主要得出以下结论：

(1)基于RBF神经网络和三次插值的曲面缺陷修复与重构策略，综合利用RBF神经网络的强非线性映射能力及三次插值的二阶连续、算法简单、易于实施等优点。

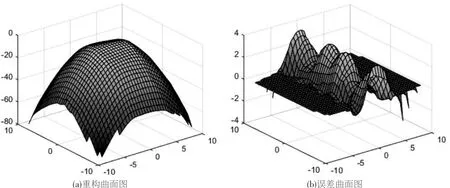
图5 基于三次插值的方法进行曲面修复与重构结果

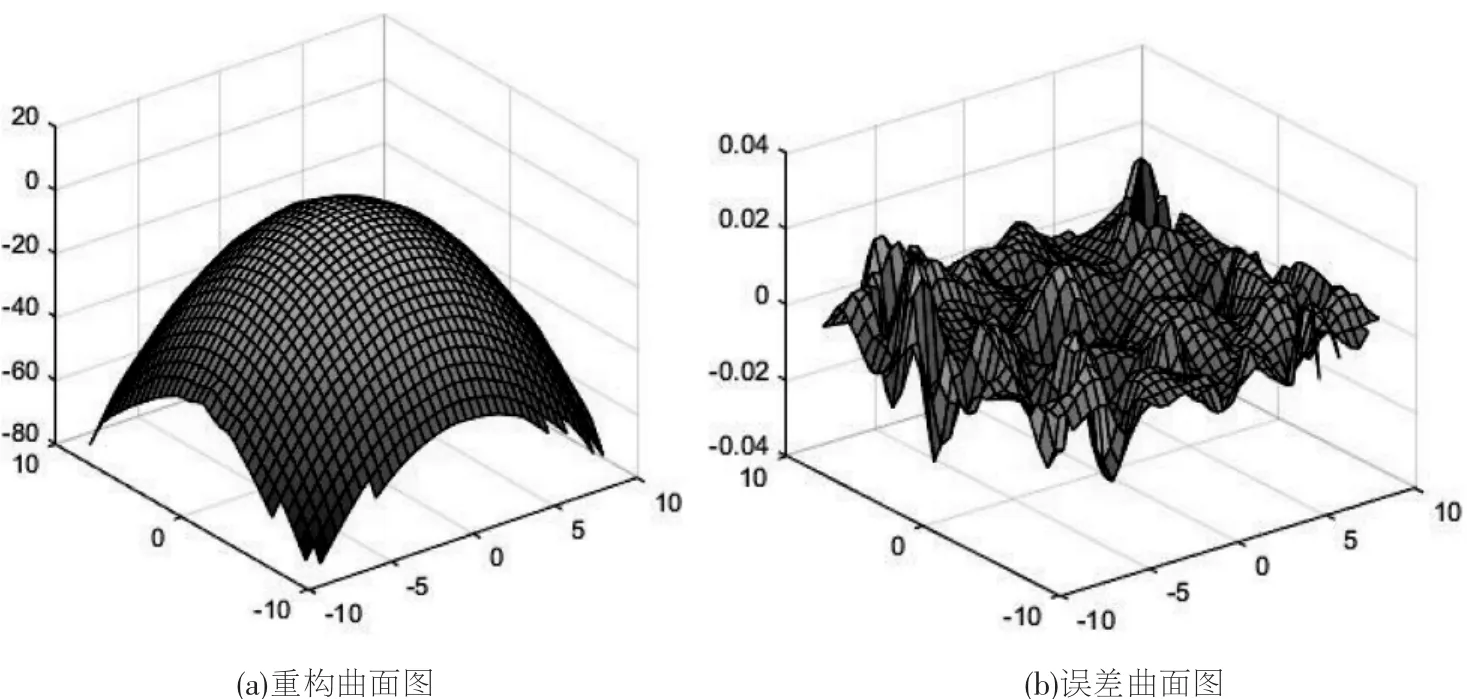
图7 基于RBF神经网络和三次插值的曲面修复与重构结果

(2)与直接采用基于三次插值的曲面修复与重构策略相比，基于RBF神经网络和三次插值的曲面缺陷修复与重构策略，具有修补精度高、操作方便的优点。

(3)所提出的RBF优化建模策略能够有效避免人为因素的影响，算法简单可靠。