利用GS算法实现图像加密技术

(安徽三联学院 电子电气工程学院,安徽 合肥 230601)

随着多媒体信息技术的发展，数字图像已经成为人们传播的主要信息，因此图像加密技术随之也成为信息安全领域的一个重要研究课题.而利用相位恢复算法来进行光学图像的加密，是图像加密的一种简单有效的手段，近年来发展迅速.相位恢复技术是指利用直接测量得到的强度信息通过迭代或者直接计算的方法得到相位，为全光场重构进而实现三维显示技术提供重要的数据信息[1]，是现代光学发展的一个重要研究领域.相位恢复算法的经典算法主要有GS(Gerchberg-Saxton)迭代算法[2]和利用强度传输方程(Transport-of-Intensity Equation，后面简称TIE)来求解相位的确定性解的求解方法[3，4].其中的GS算法可以用于图像加密技术，其加密方法灵活，加密解密过程相对简单.整个加密解密方法可以用于不同的加密系统中，如基于傅立叶变换方法的加密系统、分数傅里叶变换的加密系统等[5].总之，对于利用相位恢复算法中的GS算法进行图像加密的研究具有非常重要的意义.

1 图像加密技术的实现

1.1 GS算法原理

GS算法是相位恢复技术中的一种经典算法，而相位恢复技术是指利用直接测量得到的强度信息通过一系列计算得到物体的相位信息，从而重建原物体的波函数.相位恢复算法的主要算法有两类：GS迭代算法和基于TIE方程的方法.Gerchberg等人在1972年提出了Gerchberg-Saxton算法(简称GS算法)，主要思想是在图像空间和傅立叶空间之间利用已知的信息或者约束来重复迭代.后来国内外学者在GS算法的基础上也先后提出了很多的改进算法，提高了算法的精度和收敛速度.GS算法原理如下：设光束的光场函数为

f(x,y)=|f(x,y)|exp[iφ1(x,y)]

(1)

其对应的聚焦平面上的光场函数可以表示为

g(x,y)=|g(x,y)|exp[iφ2(x,y)]

(2)

其中,|f(x,y)|2，|g(x,y)|2为强度信息，φ1(x,y)，φ2(x,y)为相位信息.其中,f和g满足正反傅立叶变换的关系.GS算法流程图如图1所示，具体思想是任意给定一输入面上的初始相位，这里的相位可以是随机的相位.然后与入射光的振幅组合在一起，构成入射波函数f(x,y)，再对入射波函数f(x,y)作傅立叶变换，这时得到函数g(u,v)，对函数g(u,v)的相位部分，再与输出面上希望得到的振幅分布函数|G(u,v)|构成函数g′(u,v).然后对函数g′(u,v)作逆傅立叶变换，这时将得到下一步迭代波函数f′(x,y)，最后取其相位部分代入原初始相位中.重复上述过程一直到设定的迭代次数或者误差小于预先设置好的值为止.

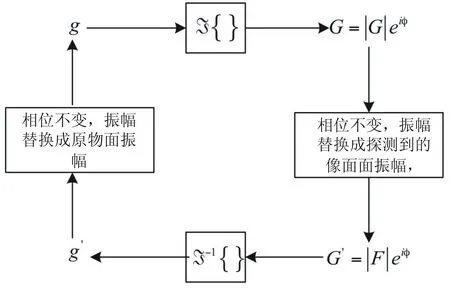
图1 GS算法流程图

1.2 利用GS算法实现图像加密

针对上述的GS算法，将基于GS算法求解出来的相位作为图像加密的密钥，通过密钥再将加密的图像解密出来，加密流程如图2所示，θ(x,y)为经过相位恢复算法处理后得到的图像全部信息的相位.对图像进行解密的时候，只需要将θ(x,y)作为相位组成的相位频谱函数进行傅里叶变换就可以得到解密后的图像.该过程可以利用MATLAB软件进行整个算法的模拟实验验证.

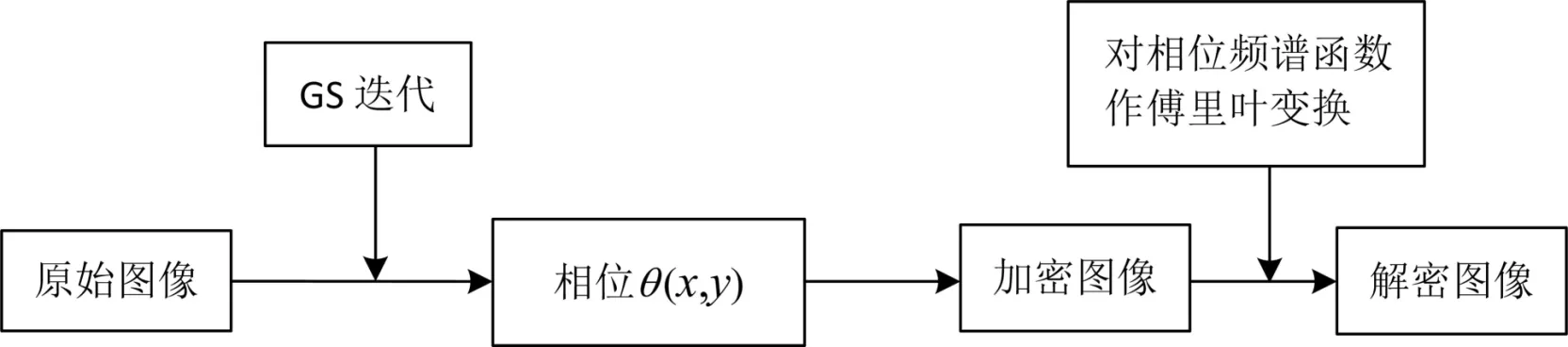
图2 图像加密与解密流程示意图

2 仿真实验及结果分析

整个实验的仿真过程基于MATLAB软件呈现.图3是原始待加密图像，该图像的相位值分布在[0,2π]区间，图像大小为256×256像素.并且假设初始相位是随机相位，物体平面的强度分布是均匀的，即I0(x,y)≡1，将随机相位和物体平面强度构成入射波函数.

图3 原始待加密图像

根据上述的GS算法流程进行迭代运算，第一次迭代次数为10次，得到的相位如图4.1所示，此时得到的相位分布图与原始待加密的图像完全不同，因此可以作为加密后的图像.而解密的时候将迭代得到的相位频谱函数进行傅立叶变换即可得到解密后的图像.解密后的仿真图如图4.2所示，解密过程简单、方便.可以看出来，图4.2的解密后的图像与原始图像有一定的差距.由于迭代次数少，导致解密的图像与原始图像有一定误差.下面研究算法的迭代次数对解密图像质量的影响.

图4.1 迭代10次的加密图像 图4.2 迭代10次的解密图像

还是以图3作为原始待加密图像，所有条件不变，利用GS算法运算迭代100次，得到的相位信息即加密后的图像分布如图5.1所示.

图5.1 迭代100次的加密图像 图5.2 迭代100次的解密图像

此时得到的解密之后的图像分布如图5.2所示，迭代100次之后解密的图像几乎与原图一致，效果很好.可见，迭代次数直接影响了图像加密后再解密的图像质量.具体随着迭代次数的增加，原始图像与解密之后的图像的误差系数如附表所示.

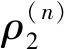
(3)

附表 迭代次数对原图与解密后图像误差的影响

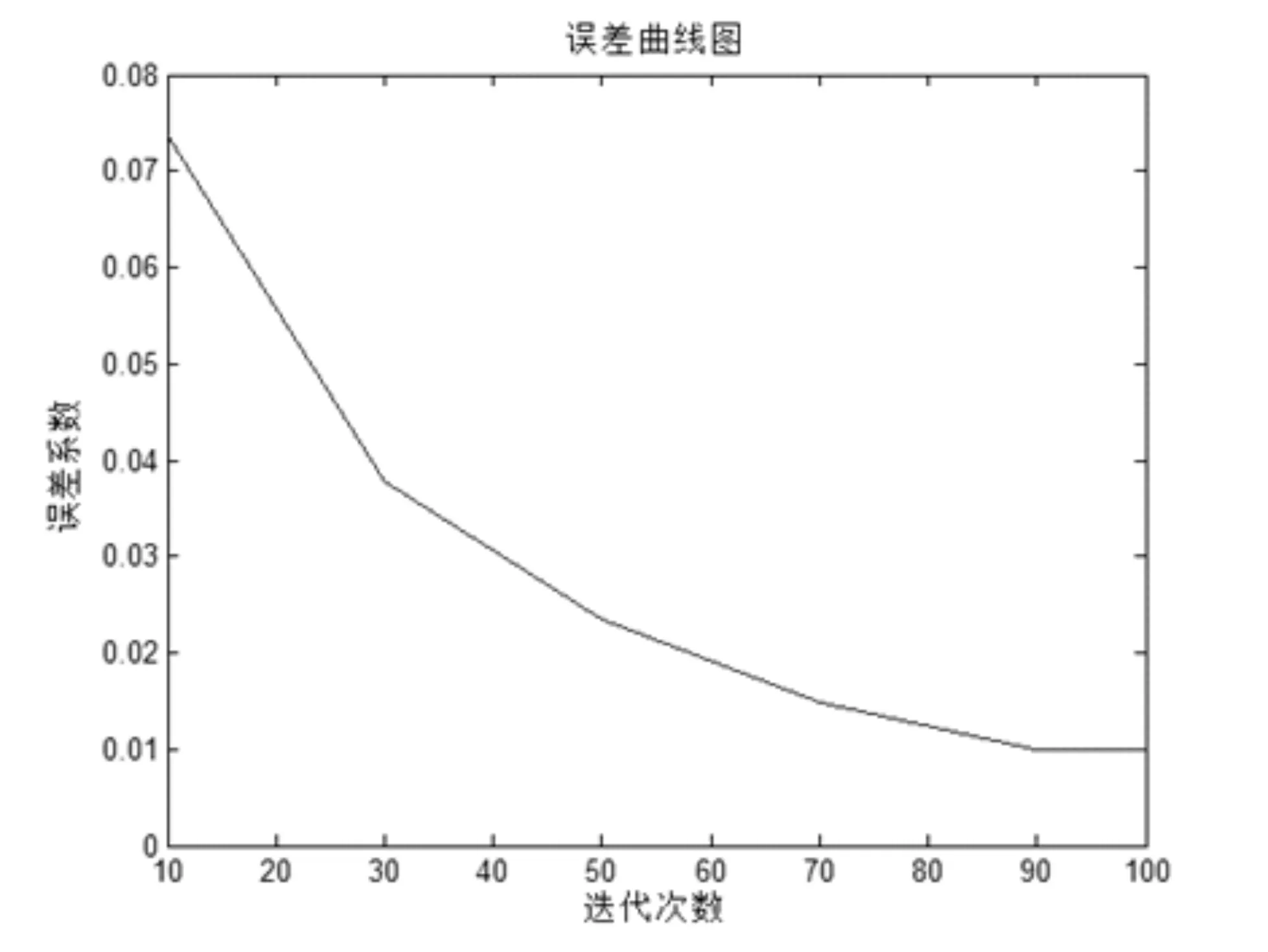
图6 误差曲线示意图

由附表所示的实验数据以及图6的迭代次数与误差系数之间的曲线示意图可以看出，随着迭代次数的增加，解密图像与原图像之间的差距原来越小.当迭代次数到达100次时，几乎与原图像一致.迭代次数从10次增加到50次之间时，随着次数增加误差显著减小.当迭代次数达到70次之后，随着迭代次数的增加，误差之间的差距变化越来越慢.

3 总 结

GS算法原理是利用波场传播的可逆性质，在两幅图像之间反复迭代，求出原始图像的相位信息，而此时通过相位信息看不出原始图像，可以作为加密后的图像.所以GS算法可以用于图像加密，解密时，只需将相位频谱做傅里叶变换即可，非常方便.而且GS算法的迭代次数，直接影响了解密图像的质量，本文对此作了深入的研究，也作了相关的仿真实验.实验表明，随着迭代次数的增加，图像解密的质量会越高，解密后的图像与原图像之间的误差系数越来越小，因而越接近于原图像.