基于改进MPS方法的弹性支撑侧壁对溃坝现象的影响分析

吴巧瑞，王 磊，谢永和，白兴兰

(浙江海洋大学船舶与机电工程学院，浙江舟山 316022)

溃坝现象的物理模型是使用挡板在水箱内维持一定高度的水柱，在初始时刻迅速撤去挡板，在重力的作用下，水柱会坍塌形成一个自由表面波，并对周围的障碍物进行砰击作用的一种现象，见图1。此现象广泛存在于各个领域，尤其在船舶与海洋结构物设计制造、海洋水动力学领域具有广泛的应用背景，经常用作甲板上浪、液舱晃荡、入水冲击、海洋平台遭受波浪载荷等工程实际问题的简化来研究，其共同点是在砰击过程中具有流体的大变形和强间断性。因此，尽管溃坝现象的物理模型非常简单，却一直吸引着大量学者对其进行研究，包括实验研究[1-3]和数值研究[4-6]，但溃坝问题仍然是大变形自由液面问题处理中的难点之一。

鉴于溃坝现象的特殊性，无网格方法越来越被广泛地应用来处理这类具有大变形自由液面的流动问题，MPS方法就是其中之一。MPS方法最早是由日本东京大学的KOSHIZUKA S，et al[7]于1995年提出的，相对于其它无网格方法，MPS方法采用预估-修正的半隐式方法来求解不可压缩流体的控制方程，从而可以有效地避免离散对流项所引起的数值发散问题，另外，粒子具有运动性并具有非常便捷的自由液面判别方法，这些都使得MPS方法在处理自由液面问题尤其是大变形问题中有其独特的优势。但同时，由于该方法提出不久，MPS方法本身在稳定性、精确性方面还存在一定的问题。因此，笔者对原始MPS方法进行了改进[8]，改进后的MPS方法采用弧度判定法和粒子碰撞模型，从而可以有效地避免粒子聚集现象和粒子的误判现象，大大提高了数值模拟的稳定性和准确性。本文采用改进的MPS方法，通过模拟固定侧壁的溃坝现象验证了该方法在溃坝问题中的有效性，探究了弹性支撑侧壁对溃坝现象中的流动形态、侧壁受力以及表面波对侧壁的砰击压力的影响规律，旨在为解决实际工程问题提供一定的借鉴。

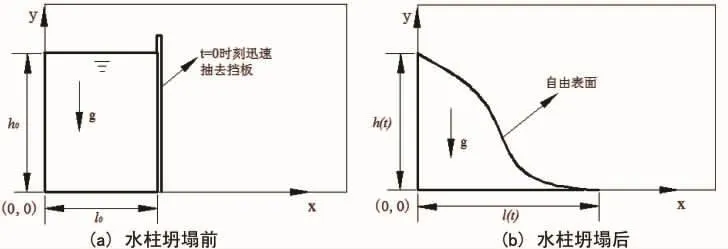
图1 溃坝物理模型图Fig.1 Physical model of the dam break

1 改进的MPS方法数值模型

对于不可压缩粘性流体，其控制方程为连续方程和N-S方程，如下所示：

其中，ρ为流体密度；v为流体质点的速度；f为外部的作用力；ρ为流体质点的压力；υ为流体的运动学粘性系数。

MPS方法是通过预估-修正求解不可压缩流体的控制方程，具体实现方法如下。

1.1 粒子相互作用模型

在MPS方法中，采用可以自由移动的粒子来离散问题域，相邻之间的相互作用是通过一个核函数来衡量，本文采用的是Koshizuka和Oka[9]在1996年提出的核函数，如下：

在该式中，r是相邻两个粒子之间的距离，re是核函数的控制半径。某个粒子的相邻粒子即在其核函数控制半径内的粒子。

粒子数密度表征的是流场中粒子的分布状态，保持粒子数密度恒定就是保证流体的不可压缩性。该参数可以通过粒子在核函数的控制域内与其周围相邻粒子的核函数数值的叠加表示，即：

式中，N是粒子i的相邻粒子总数，ri和rj分别是粒子i和粒子j的位置矢量。

梯度算子和拉普拉斯算子可以分别表示为：

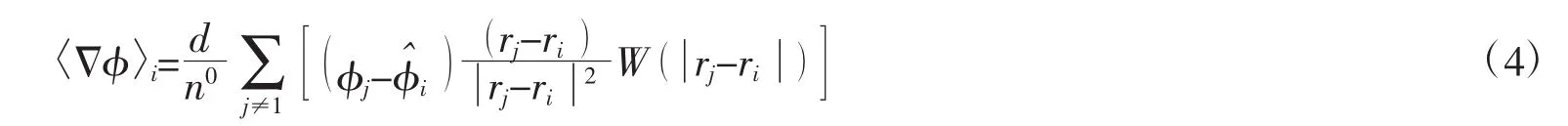
和

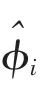
1.2 边界条件

边界条件可分为两种类型，即自由表面边界条件和固壁边界条件。

对于自由表面边界条件，首先要进行自由表面粒子的判定，原始的判定方法是根据粒子数密度进行判定，具体判定公式如下[9]：

式中，β是一个小于1的系数，一般取β=0.97。

上面根据粒子数判定自由液面粒子的方法常常导致误判现象的发生，为了克服这个问题，改进的MPS方法中采用了一种弧度判定方法，这种方法通过对某个粒子的相邻粒子相对该粒子的弧度进行叠加，如果叠加后的弧度大于等于2 π并且在（0，2 π）区间内无间断，则该粒子判定为流体内部粒子，否则为自由表面粒子，这种方法已证明可以有效避免粒子的误判现象[8]。

对于自由表面粒子，其压力赋为大气压即p=patm=0。

至于固壁条件，首先，固壁用三层边界粒子来表示，靠近流体的那一层为流体边界粒子，参与压力的计算；外层的两层粒子称为固体边界粒子，不参与压力计算。另外，为了防止内部的流体粒子穿透固体边界，当流体粒子靠近边界时，会收到固壁粒子的一个排斥力，具体计算如下[10]：

其中，r0为初始粒子间距；D=5 gh，h为水柱的初始高度；P1=12，P2=4。

1.3 计算流程

（1）根据第n个时间步的信息，通过粘性项和外力项显式预估粒子的中间速度和中间位置信息，即：

（2）通过式（3）计算粒子的中间粒子数密度信息n*，然后隐式求解Poisson方程，得到pn+1：

（3）根据pn+1对中间速度和中间位置信息进行修正，得到第n+1时间步的速度和位置信息：

（4）为了避免内部流体粒子的聚集现象，引入了一种碰撞模型，这是改进MPS方法的另外一个改进的措施。即当两个粒子之间的间距满足d＜βL0时，应用的碰撞模型如下[8]：

2 固定侧壁溃坝现象

选取的固定侧壁溃坝模型如图2所示，水箱的长度为3.22 m，高度为2 m，水柱初始高度0.6 m，位于水柱对面墙壁上的一个点P（3.22 m，0.16 m）作为压力监测点。离散模型的数据为：流体粒子7 200个，流体边界粒子723个，固体边界粒子2 196个，共计10 116个粒子。

图2 溃坝模型及离散图Fig.2 Model of the dam break and the corresponding dicretisizing model

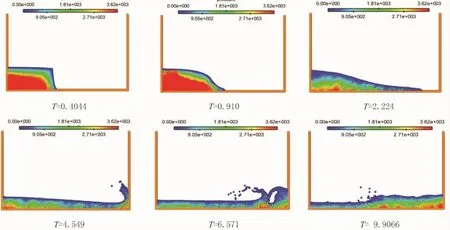
图3 溃坝过程及压力分布情况Fig.3 The process of dam break and the pressure distribution

图3给出了改进MPS方法模拟的溃坝过程中的六个典型时刻的流动现象及对应的压力分布。从图中可以看出，当溃坝现象发生后，水柱在重力的作用下发生坍塌形成了一个自由表面波或称为溃坝波，该表面波在惯性的作用下向右传播，然后与右侧壁面发生砰击现象，之后出现了自由表面的翻卷、破碎和飞溅现象，之后接着反向向左传播，能量逐渐减弱直至达到新的静平衡状态。

图4（a）给出的是溃坝波前端位置随时间的变化曲线，图4（b）给出了P点的压力随时间的变化情况，这两幅图均与对应的实验值[11]进行了比较。从图中可以看出，溃坝波大约在T=2.5附近到达右面的侧壁并紧接着发生了砰击作用，整个过程共发生了两次比较明显的砰击现象。另外，改进的MPS方法的计算结果较为平滑，与实验值吻合更好。但是，改进的MPS方法的计算结果，无论是溃坝波前端位置的变化还是P点的压力时历值，相对于实验值存在一定的延时，这种情况可能是由于数值模拟中运动学粘性系数的取值较大造成的。

图4 溃坝波前端位置和P点压力的时历曲线Fig.4 Time history of the leading edge of collapsed water column wave and the pressure at the point of P

3 弹性支撑侧壁溃坝现象

实际工程中，当发生溃坝时，由于溃坝波的巨大砰击力的作用，会导致一些建筑物的移动或旋转。因此，本文选取如图5所示的具有弹性支撑侧壁的溃坝模型，水柱右面的墙壁为弹性支撑，在溃坝波的砰击力作用下将围绕弹性支撑点做旋转运动，其转动方程为：

式中，I为惯性矩；M为转动体的质量；H为转动体质心到旋转点的距离；K为弹性支撑的刚度系数；θ为弹性支撑侧壁的转角；Mf为流体压力作用在弹性支撑侧壁上的合力矩，可按照下式计算：

其中，pi为弹性支撑侧壁粒子i处的压力；N为弹性支撑侧壁离散的粒子总数；l为粒子i距弹性支撑点的距离；dl可取为粒子初始分布间距。

具体尺寸选取如图2所示的溃坝现象的物理模型，只是右侧固壁变成了弹性支撑侧壁。在整个数值模拟中运动性粘性系数v取0.001 m/s2，计算时间步长dt为0.000 5 s。图6给出了具有弹性支撑侧壁的溃坝现象模拟结果，包括6个在整个溃坝现象中比较典型时刻点的图像，分布对应T=3.859 9、6.147 3、7.576 9、9.649 8、11.293 8和21.444 0。图7显示了在整个溃坝过程中弹性支撑侧壁的旋转角度θ随时间的变化情况，图8中给出了P点压力随时间的变化规律，图9比较了右侧侧壁在固定和弹性支撑两种情况下的所受流体合力矩随时间的变化情况。

图5 弹性支撑侧壁的溃坝模型示意图Fig.5 Illustration of dam break with elastic-supported rigid wall

图6 具有弹性支撑侧壁的溃坝现象Fig.6 Phenomenon of dam break with elastic-supported side wall

结合图6-9可以看出，当溃坝现象发生之后，水柱坍塌并形成一个溃坝波，在T=3.8附近到达右侧的墙壁，右侧侧壁所受流体的合力矩从0开始增长，在该力矩的作用下，弹性支撑侧壁开始逐渐向右侧旋转；紧接着溃坝波与右侧侧壁发生了比较激烈的抨击现象，右侧侧壁所受流体的合力矩在T=8左右达到最大值，与此同时其转角也达到最大值0.25左右；此后，溃坝波在左右两个墙壁之间反复的传播直至静止状态，右侧侧壁的旋转角度也在这个往复震荡过程中逐渐减小至0。

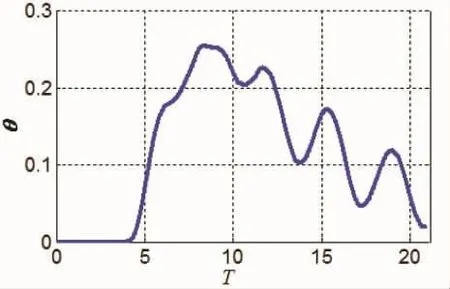
图7 转角θ随时间的变化曲线Fig.7 The time history of the rotation angle

图8 P点的压力随时间的变化曲线Fig.8 The time history of the pressure at the point of P

另外，结合前节固定侧壁的溃坝现象，弹性支撑侧壁的溃坝模型主要有以下特征：首先，具有弹性支撑侧壁的溃坝现象从溃坝发生到重新恢复平衡状态所消耗的时间要大于固定侧壁所需的时间，前者是在T大于20以后才达到静平衡状态，后者是在T=11左右。与固定侧壁的溃坝模型相比，弹性支撑侧壁的溃坝模型的整个溃坝过程和侧壁上流体压力合力矩的峰值的出现均具有一定的延迟性。其次，这两种溃坝模型右侧侧壁的压力时历曲线有明显的不同。虽然这两种溃坝模型的最大抨击压力峰值均在1.2左右，但固定侧壁模型中有两次比较明显的砰击现象，而对于弹性支撑侧壁的溃坝模型，当溃坝波到达右侧侧壁发生砰击现象时，右侧墙壁在砰击力矩的作用下向右侧旋转，弹性支撑起到了明显的延迟用，从而没有明显的第一次砰击现象。

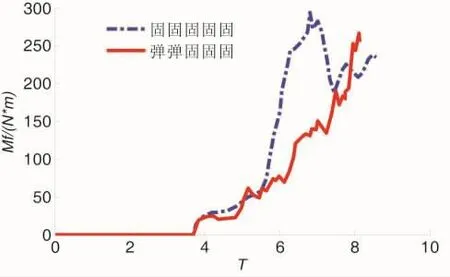
图9 右侧侧壁的流体合力矩随时间的变化曲线Fig.9 The fluid force momentum on the right-side wall

4 小结

本文基于改进的MPS方法，采用Fortran语言进行自主编程，分别模拟了固定侧壁溃坝现象和弹性支撑侧壁溃坝现象。研究证明，改进的MPS方法可以成功地模拟溃坝现象中自由液面的翻卷、破碎和飞溅现象，验证了该方法在处理这种大变形自由液面流动问题中的优势。另一方面，通过这两种溃坝模型的对比发现，虽然两种模型的最大砰击压力相近，但固定侧壁的溃坝模型有两次明显的砰击现象，弹性支撑侧壁的溃坝现象只有一次明显的砰击现象。其次，由于弹性支撑侧壁的缓冲作用，整个溃坝过程的进行出现了显著的延迟效应。