用数形结合思想解决最值问题的应用探讨
2019-05-17郑胜
郑 胜
(福建省三明市将乐县第四中学,福建三明 350300)
引 言
在数学学科的学习过程中,所谓数学思想,就是通过对数学基本知识的学习和理解,产生对数学知识本质的高度概括和认识。数形结合思想是初中数学比较重要的思想,它能把抽象的问题具体化,从而简化解决问题的过程。最值问题是初中数学中最常见的一类问题,利用数形结合思想能够提高解决这类问题的速度和准确性。
一、数形结合思想
数学中最基本的两个概念就是数与形,这两个概念是对现实世界中客观事物的抽象反映,贯穿于整个数学学习和教学过程。从广义上来说,我们可以将“数”理解为数学的文字特征,如数字、概念、数学公式、性质、定理等;“形”,我们可以将之理解为图形表征,如图像、实物等,数和形往往是密不可分的。数形结合的本质就是将抽象的数学问题转化为直观的问题,通过对数字和图形进行处理,将抽象问题具体化,将复杂问题简单化。数形结合思想是一种解决数学问题的思想方法,它是通过分析数学问题的代数和集合意义,通过数与形的结合,运用抽象思维和形象思维解决数学问题的方法[1]。
二、初中数学最值问题
在数学学习过程中,最值(最大值和最小值)是一类比较常用到数形结合思想的问题,也是初中数学学习中比较重要的内容之一。最值问题的解决需要学生具有广阔的知识面,并能灵活运用数学知识。解决最值问题要求学生不仅具有扎实的基础知识,还要具有灵活的思维,掌握解决问题的实质方法,具有创新意识,有数形结合的思想意识。
最值问题可以分为两种类型:第一种是代数中最大值和最小值的问题,如在现实生活中我们常常遇到的,利益最大、距离最短、花费最少、面积最大等问题,都是代数类最值问题。代数式的最值问题又可以分为三小类:第一类是关于方程未知数和函数变量的最值问题;第二类是求代数式的最值问题;第三类是关于数论的最值问题。第二种最值问题是几何最值问题,如在几何图形中有一个元素做规律的运动,这一元素在一定范围内变化,而与这一元素相关的量也将随之发生变化,这个变化的量存在最大值和最小值。几何最值问题又可细分为四小类:第一类是关于线段的最值问题;第二类是关于面积的最值问题;第三类是关于角度的最值问题;第四类是关于几何量的最值问题[2]。
三、数形结合思想在初中数学解决最值问题中的具体应用
初中数学最值问题主要考查学生的综合解题能力,对学习水平要求较高,而有效利用数形结合思想能够将复杂、抽象的最值问题变为简单、具体的问题。最值问题类型多样,解决的方法也很多,如何快速、正确地解决最值问题是学生比较关心的问题。在众多解决方法中,数形结合的方法是解决最值问题最好的方法,它能将最值问题转化为直观的形,也能将最值问题转化为抽象的数,如以数化形,以形换数等数形结合的方法。在求最值的过程中,通过数形结合、数形互变能够丰富学生对最值问题的认识,强化数学学习的美好体验[3]。
(一)以数化形,数形结合解决最值问题
在数学最值的学习过程中,有些数量关系比较抽象,只有简单、抽象的数据材料,在这种情况下,教师只讲解抽象的数据,无法让学生真正理解问题,因为学生的思维能力有限,对数量关系的认识比较模糊,难以正确理解所给的信息,无法体验问题的真正意图。而这时就需要教师以数化形,将抽象的数字转换为具体的形象,通过直观形象的呈现使学生对问题有正确的表征,从而在头脑中勾勒出关于问题的具体画面,并在直观认识的基础上,通过对数量关系的认识,提高解决问题的效率。
例1:求y=|2x|+x-1的最小值。
在这道题中,单纯通过一次函数的式子去求解y的最小值是很难的,教师单纯地讲解函数式也无助于学生的学习和理解,这时,教师就可以利用数形结合的思想,将数学关系式转化为函数图像,让学生在函数图像的帮助下,主动地感知函数图像的变化趋势、增减、最小值的情况。所以,教师可以让学生做出y=|2x|+x-1的图像(如图1),以观察它的增减性。
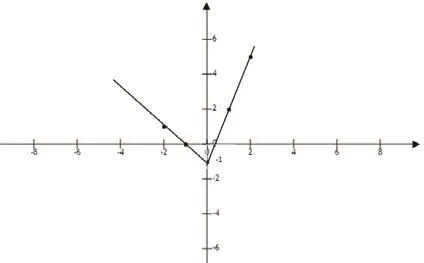
图1
通过图像我们可以发现,当x>0时,y随着x的增大而增大,当x<0时,y随着x的增大而减小,当x=0时,y=-1是最小值。
(二)以形换数,数形结合解决最值问题
图像有直观、形象的特点,能够帮助人理解问题,但是只有图形,而没有定量也很难快速解决问题。有些复杂的图形,需要借助“数”将问题数字化,从而挖掘出问题背后的数量关系。
例2:某村在修一条水渠,水渠的横断面为等腰梯形(如图2),腰与水平线的角为60°,要求水进入渠内后水渠横截面的两腰和渠底总长为6,问渠中水量的高度为多少时,水流量最大?
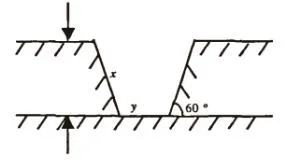
图2
在本题中,借助等腰梯形的图形,将面积最大化的问题通过图形帮助学生理解,求水流量最大也即梯形面积最大值。画出等腰梯形的图形,设等腰梯形的腰为x,下底边为y,横断面积为S,根据两腰和渠底总长为6,则2x+y=6,h=xsin60°,所以
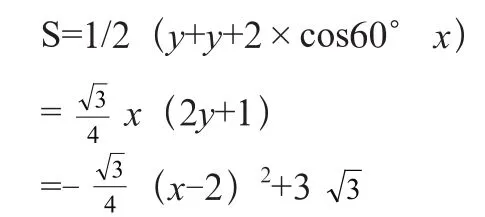
当x=2时,面积最大为此时
结 语
综上所述,在初中数学学习过程中,利用数形结合思想,能够以数化形,以形换数。用数形结合的思想解决最值问题,能够将具体和抽象,简单和复杂互换,从而培养学生的数学思维,提高学生的数学分析能力、学习效率。
