初中数学“综合与实践”活动研究—例谈问题解决理论下的数学建模活动

吴 威

（福建省福州第一中学，福建福州 350000）

引 言

在本文的数学建模活动研究中，问题解决模式为：指导教师引导学生从现实中提取信息，与已学的知识加以联系，并进行信息加工，从而将现实问题转化为数学问题，在自身能力所及的范围内解决此问题，再争取将数学问题的解决应用到实际生活中[1]。

一、问题解决理论下的数学建模活动

强调“问题解决”是目前构建数学课程改革的重要趋势。目前的国际数学课程改革强调以下三点：（1）强调“解决问题和数学应用”；（2）强调“综合活动”，我国《全日制义务教育数学课程标准》中强调，在初中学段，学生将进一步参与综合实践活动，探讨一些具有挑战性的研究课题，发展应用数学知识解决问题的意识和能力；（3）强调“非常规问题”。

二、“测量学校内建筑物高度”的建模过程和指导

（一）原始问题

测量建筑物高度是一个常见的数学问题。测量的方法可以以几何为主，也可以结合三角方法和物理方法，如求线段长、相似三角形、气压性质、自由落体试验、几何光学试验等。

测量的对象：（1）本校旗杆的高度；（2）校外高建筑物（不可及）的高度。

（二）实施过程

（1）学生。小组成员经过讨论，需要确定建模过程中的小组成员分工、测量目标、测量方式和测量工具，及时记录测量数据，做好多种方法的设计。有能力的小组可以做误差分析。

（2）教师。指导学生查阅资料，了解相关的测量方法和技巧。鼓励学生合作完成测量，不局限测量的方式。对学生提出的新颖的测量方式要及时加以引导和组织讨论；在测量过程中，对学生不合理的方法和做法，要适当地引导他们发现问题，让他们自己寻求解决方法，也可以将其作为反思的例子；在学生完成测量后，组织各小组进行讨论交流，让学生将测量结果、测量方式、误差估计方式等一一做交流，让学生谈谈自己的收获。

（三）测量方法总结报告

（1）测量本校旗杆的高度。由于学校的旗杆下有阶梯和底座，因此可以将这个模型看作被测建筑物底部不可到达的模型。

方法一：鉴于旗杆的前方是空旷的操场，选择测量的位置比较自由，C组利用量角器测量，运用三角函数知识求值（见图 1）。

①设旗杆建筑MN底部的阶梯高度为m，在旗杆建筑底部N所在的水平面上，选取A，B两个位置，使A，B，N三点共线；

②在人眼的位置，分别测量A，B两个位置的仰角，测得仰角的度数为x，y，两观测点间的距离AB=a，人眼高度AA'=b；

图1

方法二：由于在试验中发现，利用量角器测量仰角得到的数据误差比较大，于是D组同学将C组的方法做了改进，不测量角度，转而利用三角函数定义，测量三角形两边之比（见图 2）。

①设旗杆建筑MN底部的阶梯高度为m，在旗杆建筑底部N所在的水平面上，选取A，B两个位置，使A，B，N三点共线，人眼的位置为A'和B'；

②分别在C，D位置竖一根杆子，使人的视线经过杆的顶端时，刚好能看见旗杆的顶端M，测量BD，AC间的距离a和b，A，B两个位置间的距离c，杆子的长度DD'为h，在D位置到旗杆的距离DN为d，设MB高度为x，人的高度为n；

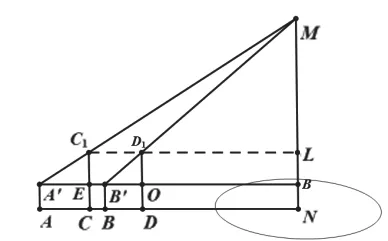
图2

如果有平面镜等工具，也可以利用平面镜放射等光学原理来设计试验。

2.在校内测量校外高建筑物的高度

由于校外的楼比较庞大，学生在校内测量，楼底被遮挡，测量遇到一定困难。

方法一：由于在校内有教学楼（其他建筑物）可以利用，教师指导C组学生采取与上文测量旗杆相类似的方法，在竖直方向选择两个测量点进行操作（见图3）。

①在教学楼底部A的竖直方向上，再找一个测量点C（在教学楼的一层）；

②分别测量A'和C两个位置的仰角，测得仰角的度数为x和y，测得人眼高度AA'=b，教学楼一层的高度为a；

图3

与此方法同理，学生也可以借助之前试验中求得的教学楼高为数据进行计算。

方法二：考虑到高建筑物在学校外，无法看到其底部，因此无法准确判断点是否与建筑物底部质点共线，容易产生误差。D小组的学生没有采用测量旗杆的方法，而是结合平面几何的知识，即三角形中线定理给出了一个更具普遍性和应用性的方法（见图4）。

①由于被测的高楼比较庞大，楼底被遮挡难以确定位置。因此，在被测对象前方，也就是学校内，与被测高楼同一水平面上任取共线的三点A'，E'，D'，使E'为A'D'的中点；

②测得AE=ED=a，学生分别站在A'，E'，D'处测量仰角，测得 ∠BAC=x,∠BEC=y,∠BDC=z，人眼高度为m，

设AB=b,BE=c,BD=d，BC=x；

③根据中线定理，可得b2+d2= 2a2+ 2c2，

由三角函数知识可以得知：b· ta nx=c· ta ny=d· ta nz=x， 由 此可得则被测高楼的高度为

图4

三、模型结果和评估

（一）测量本校旗杆的高度

在实际模拟中，测得a=5m，b==1.5m， 44x= °， 65y°= ，m=0.6m，代入得

由于大多数学校的旗杆高度为10米到12米，因此借助测角仪测得的数据，用于模拟计算旗杆高度较为准确。

但这种设计方式，对于较远的建筑而言，由于底部看不清位置，无法准确选定三点共线的位置，估算的数值容易有较大误差。

（二）在校内测量校外高建筑物的高度

由于校外的楼比较庞大，学生在校内测量，楼底被遮挡，无法看到其底部，因此无法准确判断点是否与建筑物底部质点共线，容易产生误差， 操作时采取方法二，即被测高楼的高度为测 得x= 7 0°，y= 6 5°z=62°，m=1.5m，a=10m， 代 入 得

结 语

在建模过程完成后，学生需要回顾自己已经解决的模型，正视自己正在解决的模型，展望自己能够解决的模型。在将自己的新想法付诸实践时，需要不断地学习、改进，使这些观念适合现实的问题情境。由此可见，通过数学建模活动，能够有效培养学生的问题意识、知识应用意识和创新意识，在活动中使学生积累经验，提高学生解决现实问题的能力。