指数式及对数式比较大小试题的三种常见题型*
2019-05-15福建省龙海第一中学新校区363100苏艺伟陈艺平
福建省龙海第一中学新校区(363100) 苏艺伟 陈艺平
比较大小试题经常出现在高三年的综合卷以及高考试题当中.此类试题不仅能够综合考查指数、对数、幂函数的运算性质、图像、单调性等,还能够与导数、不等式相结合.试题虽然简短却内涵丰富,集指数、对数、幂函数、不等式等众多的知识点于一体,体现了在知识交汇处命题的原则,较好地考查学生的数学核心素养.
类型一 直接借助函数的性质比较大小
此类题型主要考查考查指数、对数、幂函数的运算性质,要求考生能够借助指数函数(或者幂函数)、对数函数的单调性、图像分析问题,并且综合运用不等式的相关知识进行求解,对考生的计算求解能力,推理论证能力提出了较高的要求.
例1(2016年全国I卷选择第8题)若a>b>1,0<c<1,则( )
A.ac<bcB.abc<bacC.alogbc<blogacD.logac<logbc
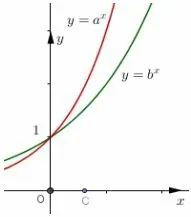
图1
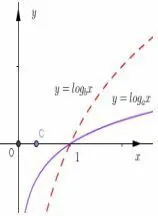
图2

图3
解析(1)比较ac和bc.
对于ac和bc,观察到它们底数不同,指数相同,因而可以采用两种方法来进行比较.
方法1构造幂函数.
令y=xc,由c>0可知该函数在(0,+∞)单调递增.因为a>b,故ac>bc.
方法2_构造两个指数函数.
令y=ax和y=bx,因为a>b>1,故如图1所示,由0<c<1得ac>bc.
综合上述分析可知,ac>bc,故A答案错误.
(2)比较logac和logbc.
观察到这两个对数式底数不同,真数相同,因此构造两个对数函数进行比较.令y=logax和y=logbx,因为a>b>1,故如图2所示,由0<c<1得logbc<logac<0.因此,logbc<logac<0,故D答案错误.
(3)比较abc和bac.
abc-bac=ab(bc-1-ac-1),由a>b>1,c-1<0,结合图1可知0<ac-1<bc-1<1.故bc-1-ac-1>0,则abc-bac=ab(bc-1-ac-1)>0.因此abc>bac.故B答案错误.
(4)比较alogbc和blogac.
由于alogbc=logbca,blogac=logacb,从而可以转化为比较logbca与logacb的大小.由于a>b>1,c-1<0,故0<ca<cb<1.结合图3可知,logbca<logacb,即alogbc<blogac.故C答案正确.
例2 (2017年全国I卷选择第11题)设x,y,z为正数,且2x=3y=5z,则( )
A.2x<3y<5zB.5z<2x<3y
C.3y<5z<2xD.3y<2x<5z
(思路1作差法.)
令2x=3y=5z=k,由于x,y,z为正数,所以k>1.则有x=log2k,y=log3k,z=log5k,因此2x=2log2由于故2x>3y.由于故2x<5z.综上,有3y<2x<5z.
思路2作商法.
令2x=3y=5z=k,由于x,y,z为正数,所以k>1.则有x=log2k,y=log3k,z=log5k,因此2x=2log2k=由于故2x>3y.由于故2x<5z.综上,有3y<2x<5z.
例3(2018年全国II卷选择第12题)设a=log0.20.3,b=log20.3,则( )
A.a+b<ab<0 B.ab<a+b<0
C.a+b<0<abD.ab<0<a+b
解析根据对数的性质可知a>0,b<0,故ab<0.由于log0.30.4>0,log0.30.2>0,log0.32<0,因此即即a+b>0.因此选D.
例4 (2018年天津卷选择第5题)已知a=log2e,b=ln2,则( )
A.a>b>cB.b>a>cC.c>b>aD.c>a>b
解析根据对数的性质可知a∈(1,2),又c=log23>log2e,即c>a,因此有c>a>b.
类型二 指数式、对数式以自变量的形式出现
在此类试题中,指数式、对数式是以自变量的形式出现.题目会给出一个函数(可能是具体函数也可能是抽象函数),需要先考察该函数的单调性,然后比较自变量的大小,进而结合单调性求解.
例5(2017年天津卷选择第6题)已知奇函数f(x)在R上是增函数,g(x)=xf(x).若a=g(-log25.1),b=g(20.8),c=g(3),则a,b,c的大小关系是( )
A.a<b<cB.c<b<aC.b<a<cD.b<c<a
解析由于奇函数f(x)在R上是增函数,所以当x>0时,f(x)>0.显然g(x)=xf(x)为偶函数,a=g(-log25.1)=g(log25.1).由于g′(x)=f(x)+xf′(x),故当x>0时,g′(x)>0,g(x)在(0,+∞)上是增函数.因为20.8<2,log24<log25.1<log28,结合g(x)在(0,+∞)上的单调性可知b<a<c.
例6已知函数f(x)=ex-a+e-x+a,若3a=log3b=c,则( )
A.f(a)<f(b)<f(c) B.f(b)<f(c)<f(a)
C.f(a)<f(c)<f(b) D.f(c)<f(b)<f(a)
解析由于f(2a-x)=e-x+a+ex-a,因此f(2a-x)=f(x),所以f(x)的图像关于直线x=a对称且f(x)在(a,+∞)上单调递增.由图4可知,a<c<b.因此f(a)<f(c)<f(b).
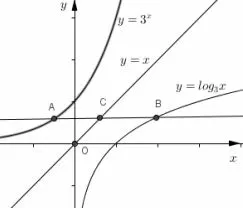
图4
例7设函数f(x)满足f(1+x)=f(1-x),且f(x)是[1,+∞)上的增函数,则的大小关系是( )
A.a>b>cB.b>a>cC.a>c>bD.c>b>a
解析由已知有函数f(x)的对称轴为x=1,f(x)在[1,+∞)上单调递增,在(-∞,1)上单调递减.由于结合f(x)的单调性可知a>b>c.
例8已知偶函数f(x)在(0,+∞)上单调递增,则( )
A.f(2e)>f(-3e) B.f(e2)>f(-e3)
C.f(log0.50.5) D.
解析易知答案A,B错误.由于即即故结合f(x)在(0,+∞)上单调递增,有答案D正确.由于-1,故结合f(x)在(-∞,0)上单调递减,有答案C错误.
类型三 自行构造函数
此类试题,题目不会直接告知相关的函数,需要根据题目给出的指数式,对数式的结构特征灵活构造出恰当的函数,进而考查该函数的单调性,结合单调性求解.
例9下列命题为真命题的是____.

解析构造函数令f′(x)=0得x=e2.易知f(x)在(0,e2)单调递增,在(e2,+∞)上单调递减,且最大值为如图5所示.
(1)由f(3)<f(4)得即所以(1)正确.
(2)由f(e)<f(π)得即所以(2)错误.
(3)由f(15)>f(16)得即所以(3)正确.
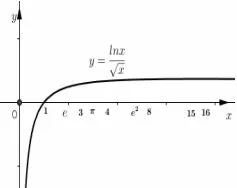
图5
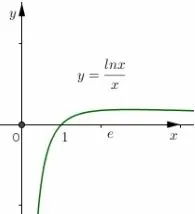
图6
例10 找出e3,3e,eπ,πe,3π,π3中的最小者和最大者.
解析根据指数函数的单调性有e3<eπ,3e<3π,πe<π3.构造函数令f′(x)=0得x=e.易知f(x)在(0,e)单调递增,在(e,+∞)上单调递减.如图6所示.由f(e)>f(3)>f(π)得得e3>3e;由得3π>π3;因此有3e<e3<eπ,πe<π3<3π.故最小值应该在3e与πe中产生,最大值应该在eπ与3π中产生.根据幂函数的单调性有πe<3e,eπ<3π.故最小值为πe,最大值为3π.
例11(同例2)设x,y,z为正数,且2x=3y=5z,则( )
A.2x<3y<5zB.5z<2x<3y
C.3y<5z<2xD.3y<2x<5z
解析令2x=3y=5z=k,由于x,y,z为正数,所以k>1.则有x=log2k,y=log3k,z=log5k,因此构造函数
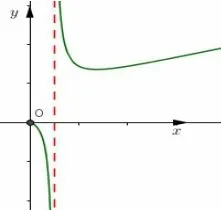
图7
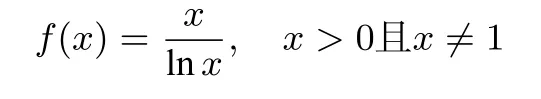
f′(x)=令f′(x)=0得x=e.显然f(x)在(0,1)和(1,e)上单调递减,在(e,+∞)上单调递增.如图7所示.由于3<4<5,所以f(3)<f(4)<f(5),即又lnk>0,因此有3y<2x<5z.
例12 已知定义在R上的函数y=f(x)满足:函数y=f(x-1)的图像关于直线x=1对称,且当x∈(-∞,0)时,f(x)+xf′(x)<0成立.若则( )
A.a>b>cB.b>a>cC.c>a>bD.a>c>b
解析由已知有y=f(x)为偶函数.令g(x)=xf(x),则为g(x)奇函数且在R上单调递减.显然b=g(ln2),c=g(-2)=-g(2).由于故-c<b<a<0,因此有c>a>b.
不难看出,与指数式,对数式相关的比较大小试题,集指数函数,对数函数,幂函数,导数,不等式等众多知识点于一体,综合性强,能够较好地检测考生是否掌握了基本知识,基本方法,基本技能,能够体现出对数学核心素养的考查,因而受到命题者的青睐.在实际解题中,要灵活根据题目条件选择恰当的方法,以期达到解题效果的最优化.
练习题
1.(2016年全国III卷选择第6题)
A.b<a<cB.a<b<cC.b<c<aD.c<a<b
2.(2014年全国辽宁卷选择第3题)
A.a>b>cB.a>c>bC.c>a>bD.c>b>a
3.(2013年全国II卷选择第8题)
设a=log36,b=log510,c=log714,则( )
A.c>b>aB.b>c>aC.a>c>bD.a>b>c
5.设a=3,b=3log3π,c=πlog3π,比较a,b,c的大小.
