加强局部简便计算的点在多边形内的高效判定

王盛春，王文成，谭雪晗，李 静



加强局部简便计算的点在多边形内的高效判定

王盛春1,2，王文成1,2，谭雪晗1,2，李 静3

(1. 中国科学院软件研究所计算机科学国家重点实验室，北京 100190； 2. 中国科学院大学计算机科学与技术学院，北京 100190； 3. 中国科学院动物研究所动物进化与系统学院重点实验室，北京 100101)

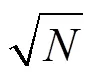
多边形；网格；简便计算；点在多边形内的检测

点在多边形内的判定检测(point-in-polygon test)是计算几何中一个基本问题，在计算机图形学、模式识别、卫星定位系统及地理信息系统等方面有着广泛的应用[1]。该问题的基本描述为：给定一个多边形与一个任意的点，判断点是否位于多边形内。

点在多边形内的判定检测算法可以分为2类：①算法不需要预处理，直接对多边形进行某些参数的计算得到判定结果，如常见的射线法[2-3]、转角法[4]、面积和法[5]等。其中，经典的射线法(ray-crossing)通过从测试点向某方向作一条射线，根据该射线与多边形边的交点数目的奇偶性进行判定。若交点数目为奇数，则该点位于多边形内；否则位于多边形外。这类算法简单直观，可处理任意多边形，通常被用作与其他算法对比的基准算法。但这类算法需要逐边操作，计算时间复杂度为()。②算法通过预处理，将多边形分解为简单几何形状并进行有序管理，如梯形法[6-7]、凸剖分法[8]、层次三角形法[9]等，或建立高效的空间划分结构，如均匀网格法[1,10-11]、分层法[12]、BSP树法[8,13]等。通过预处理的组织管理，这类算法能够降低判定计算的复杂度，如凸剖分法[8]复杂度为(log2)，其中为多边形的边数。文献[1]对这些算法进行了对比分析，并提出一种基于均匀网格的简便快速算法。近年来，学界虽然提出了一些新的相关算法，如文献[14]提出的一种基于sign()函数的点在多边形内外判别算法，将二维平面内的点转化为三维空间在平面上的点，借用符号函数判断待测点与多边形的位置关系，但在计算效率上，仍与文献[1]有所差距。

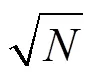
本文在文献[1]算法的基础上进行如下改进，以进一步提高检测速度：

(1) 本文将网格中心点属性的计算，转换为网格线交点属性的计算，并记录各网格交点一侧(本文为其右侧)的网格边与多边形边的相交情况。这样，在计算多边形的边与网格单元相交的情况时，即可同时进行这些计算，避免了另行计算网格单元中心点属性的计算。

(2) 不同于文献[1]仅记录与其相交的多边形的边，本文方法记录位于该网格中的多边形的边片段。由于边片段的缩小，在测试线与多边形的边进行求交计算时，可基于简单的坐标对比大幅剔除不相交的边，提高求交测试效率。

(3) 将测试点与附近已知属性的网格交点的连线，转换为与坐标轴平行的2条相连的直线段。这依然遵循了射线法的基本原则，但与坐标轴平行的直线段与多边形的边的求交计算，可简化以加速。

1 改进算法

本文提出的新方法仍基于均匀网格方法，包括2个阶段：预处理和判定计算。

(1) 预处理。首先建立均匀网格；然后记录网格线与多边形边的交点坐标以及各个网格单元中所包含的边的片段；最后逐个计算网格交点位于多边形内/外的位置属性。在该属性计算时，位于包围盒最外围的网格交点一定是位于多边形外的(所取的包围盒比多边形的紧致包围盒稍大一点)，而其他网格交点的位置属性可依据其邻近已知属性的网格点、其之间连线与多边形的边的相交次数，即可获得。

(2) 判定计算。首先确定待测点所在的网格单元；然后沿轴方向向邻近网格边做垂线，基于该垂线在网格边上的交点得到最近网格交点，形成一条平行轴的连线；最后根据以上这两条平行于坐标轴的线段与多边形边的交点个数的奇偶性与网格交点的位置属性，即可判断待测点的位置属性。

1.1 算法概述

1.1.1 预处理

预处理过程包括：创建均匀网格、记录多边形与网格边的交点坐标、记录各个网格单元包含的多边形边的片段和计算网格顶点的位置属性4部分。

与其他均匀网格法类似，由于网格分辨率的大小决定网格创建的效率和后期测试点属性判断的速度，因此，创建网格时需确定网格的分辨率。通常，网格的分辨率越高，则判定的时间越短。然而，当网格的分辨率越高，预处理时间与存储空间也将增加。因此，在实际应用中，需要同时考虑到预处理时间、判定时间和存储空间来决定优化的网格分辨率。本文采用与文献[1]相同的方法确定网格的分辨率，即设网格的宽长比为，多边形的边数为，则和方向上的单元数分别为

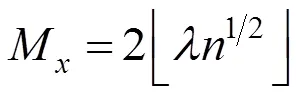
文献[1]在确定网格分辨率之后，采用数字微分分析器(digital differential analyzer，DDA)[15]算法将通过每个网格单元的整条边记录在相关单元中。由于整条边与多个网格单元相关，求交测试时难以基于简单的坐标对比剔除不相交的边。对此，本文通过计算多边形边与网格边的交点，得到各网格单元中多边形边的片段。这样，基于简单的坐标对比，可提高剔除不相交边的概率，有利于加速。

各网格线与多边形边的交点，可形成顺序排列的数组。由于各条网格线的某一坐标值是相同的，因此本文方法仅存储网格线上变化的坐标值，从而降低存储空间的消耗量。由此，各网格交点，可基于其之间连线上的交点个数，得到其位置属性。

图1为计算网格顶点位置属性的一个实例。最外层网格边上的网格点均位于多边形外，如蓝色点所示。与文献[1]类似，根据已知位置属性的网格交点，考察相邻网格点间连线与多边形边的相交次数，可推知相邻网格点的位置属性。以未知邻近网格点(3,1)为例，已知(3,0)点位于多边形外，网格边(3,0)(3,1)与1条多边形的边相交，因此(3,1)点位于多边形内。同理，由于网格边(3,1)(3,2)与多边形的边没有相交，可推知(3,2)点位于多边形内。

1.1.2 判定计算

在确定一个待测点的位置属性时，本文方法首先确定待测点所在的网格单元；然后沿轴方向向邻近的网格边做垂线，基于该垂线与网格边的交点找到最近网格顶点，形成一条平行轴的连线，最后依据两条平行于坐标轴的线段与多边形边交点个数的奇偶性与网格交点的位置属性，判断待测点的位置属性。

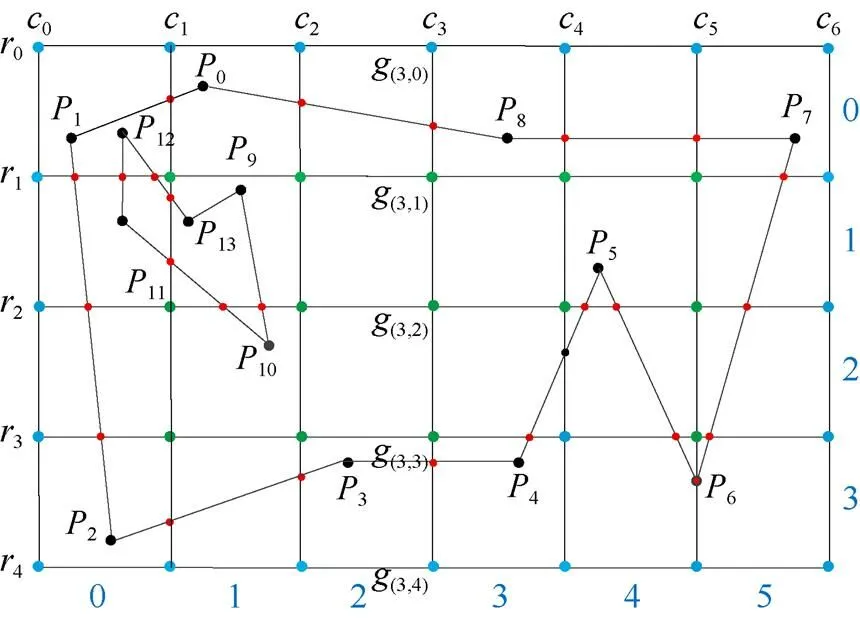
图1 计算网格点位置属性的实例图

以图2中的待测点1为例。首先，定位1点位于网格单元[1,1]中，并从待测点1出发向邻近的网格边做垂线交于点1。连接点1与其左侧的网格点(1,1)。最后，遍历网格单元[1,1]中的所有边，计数与线段11有交点的边。同时依据网格边1对应的交点存储数组，统计线段1(1,1)间的交点个数。将2条测试边与多边形边相交点的个数相加，交点总个数为1。因此，待测点1与网格点(1,1)的位置属性相反，位于多边形外。

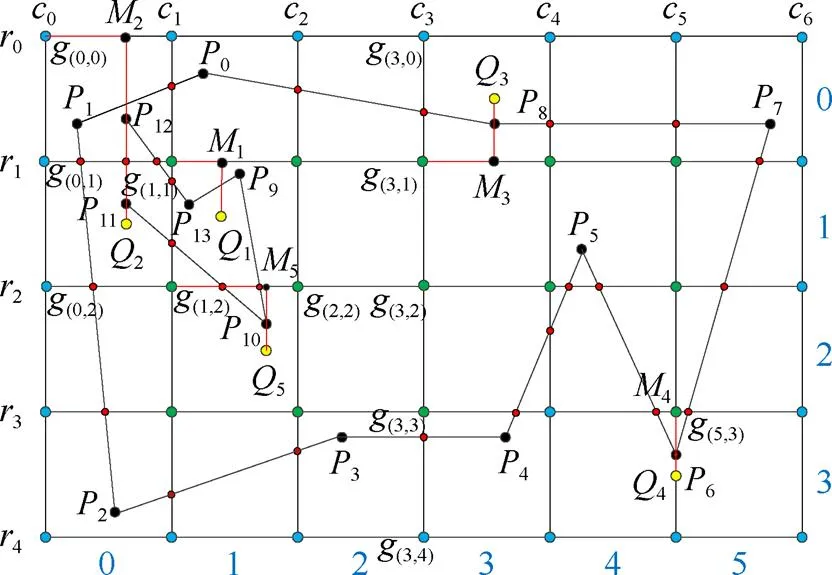
图2 点包容性判定实例图

在本文算法的判定计算中，最主要的工作是检测测试边的垂线是否与网格单元内的边相交。对此，可在该垂线向上与向下两个方向的线段中，选取较短者进行处理，以利于减少相交边的计算。如图3所示，对于垂线段1：1，考察其与一条多边形边的片段1：(设的坐标为(1,1)，的坐标为(2,2))的相交情况，可按下式进行

当进一步处理上述结果时，根据边片段1的方程计算垂线1与边片段1交点的轴坐标1；然后，与垂线段1的轴坐标范围(设1的轴坐标范围为(,))比较，判定垂线段1是否与边片段1相交。具体比较方法如下

由此，对于不相交的边，本文能够基于简单的坐标比较实现快速剔除；对于相交的边，与传统斜边求交中需要4次叉积运算和4次比较不同，本文方法只需1次乘法、1次加法和2次比较即可完成判定。

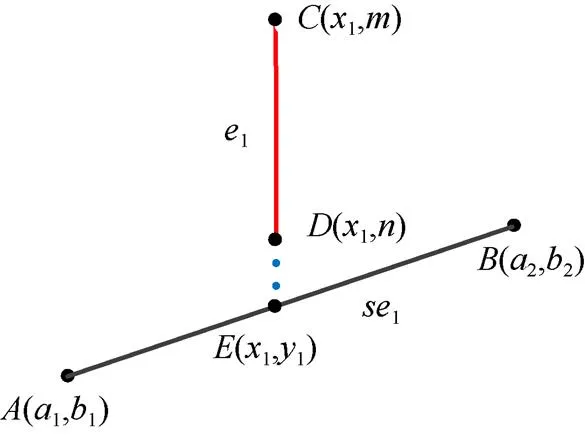
图3 判断垂线与多边形边是否相交实例图

1.2 奇异情况的处理

本文方法的本质是射线法的局部化实现，当多边形的边或顶点位于射线上时(奇异情况)，将提高相交次数统计的复杂性。

奇异情况主要分为2大类：测试线与多边形顶点相交的奇异点情况和测试线与多边形的边共线的奇异边情况。经分析，该奇异情况可分为以下4种情况处理，图4和图5分别展示了奇异点与奇异边的4种奇异情况。

(1) 若多边形顶点位于网格边上(或与网格交点重合)且连接该顶点的2条边位于该网格边异侧，如图4A区和图4C区，则该网格边(如1)关于这个多边形顶点的交点个数记为1；

(2) 若多边形顶点位于网格边上(或与网格顶点重合)且连接该顶点的2条边位于网格边的同侧，如图4B区和图4D区，则交点个数记为2；

(3) 若多边形的边与网格边重合且连接该边的2条边位于网格边的异侧，如图5B区和图5D区关于网格线1和3的情况，则交点个数记为1；

(4) 若多边形的边与网格边重合且连接该边的2条边位于网格边的同侧，如图5A区和图5C区关于网格线0和2的情况，则交点个数记为2。

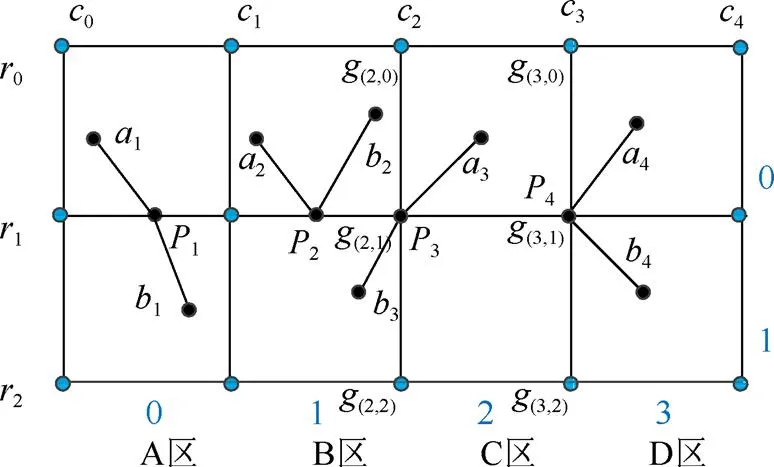
图4 奇异点的相关情况

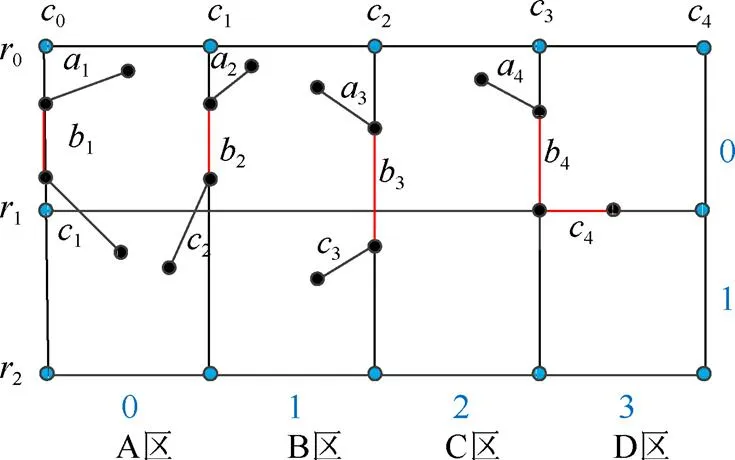
图5 奇异边的相关情况

在预处理过程中，只需对奇异点/边进行标注即可。在判定计算中，测试线遇到奇异点/边时，则沿着其方向继续前行，直至遇到非奇异情况，然后进行相关处理即可。文献[16]将文献[1]中的方法扩展到三维空间中，并对奇异情况进行了详细的分析。一般情况下，在奇异边继续向前延伸中，最多延伸两次即可得到非奇异情况。

1.2.1 预处理

预处理阶段的基本操作就是统计2个网格点之间的交点个数，然后根据交点个数的奇偶性判定网格点的位置属性。就奇异点而言，可以图4中网格点(2,2)和(3,2)进行分析，假设网格点(2,0)和(3,0)的位置属性为多边形外。在确定网格点(2,2)位置属性时，首先需要向上搜索邻近的网格点，由于网格点(2,1)为奇异点，因此向上搜索至网格点(2,0)。统计网格点(2,0)和(2,2)之间的交点个数，并依据上述的方法，连接顶点3的2条边位于网格边的异侧，交点个数为1，因此网格点(2,2)和(2,0)的位置属性相反，位于多边形内，结论正确。同理，确定网格点(3,2)的位置属性，依据上述的方法，网格点(3,2)和(3,0)之间的交点个数为2个，因此网格点(3,2)与网格点(3,0)位置属性相同，位于多边形外，结论正确。就奇异边而言，只需将奇异边看作成一个奇异点，采用与奇异点相同的方法进行计算。

在奇异情况的处理过程中，最主要的操作是判断奇异点/边两端的边是否处于奇异点/边的同侧或者异侧。对于该问题，可通过比较2条边的顶点坐标解决。以图5A区为例，该情况的奇异边垂直轴，可设方程为，因此，通过对比奇异边两端边的坐标值就能够判断出相应边的分布情况。若1边2个端点坐标的值均不小于(或均不大于)值且1边两个端点坐标的值均不小于(或均不大于)值，则边1和1处于奇异边1的同侧；反之，边1和1处于奇异边1的异侧。同理，对于平行轴的奇异边，只需通过对应的轴坐标值的比较即可得出结果。

1.2.2 判定计算

判定阶段的奇异情况主要包括：测试边与网格边重合、测试边与多边形的边重合和测试边经过多边形的顶点。对于该类奇异情况，可以采用类似奇异边的方式进行计算。

(1) 对于测试边与网格边重合的奇异情况。其处理方法为：直接根据待测点与邻近网格点间的交点个数的奇偶性确定待测点的位置属性。如图2中的待测点4，其测试边与网格线重合。因此可以通过连接待测点4与网格点(5,3)，然后根据该线段之间的交点个数确定待测点4的位置属性。由于该测试边通过多边形的顶点6，且与该顶点相连的两条边位于测试边的异侧，交点个数为1。因此待测点4的位置属性与网格点(5,3)位置属性相反，位于多边形外。

(2) 对于测试边与多边形的边重合的奇异情况。其处理方法为：延伸测试边，直至穿出多边形的边，并交于邻近的网格边，然后连接到与其交点最近的网格点，最后统计测试边与多边形的交点个数，以此确定待测点的位置属性。如图2中的待测点2，其测试边与多边形边1211重合。依据上述规定，延长测试边使其与网格线0交于点2，同时连接点2与网格点(0,0)。统计测试边与多边形边的交点个数，由于边1211两端连接的边处于测试边的同侧，其交点个数记为2。另外，测试边与多边形边10相交，交点总数为3，因此，待测点2的位置属性与网格点(0,0)位置属性相反，位于多边形内。

(3) 对于测试边经过多边形的顶点的奇异情况。其处理方法与预处理阶段的奇异点情况相似，可利用相同的处理方法进行计算。如图2中的待测点3和5，其测试边分别经过顶点8和10。由于连接顶点8的两条边处于3测试边的两侧，且连接顶点10的两条边处于5测试边的同侧，测试边33，55与多边形的交点个数分别为1和4。因此3的位置属性与网格点(3,1)的位置属性相反，位于多边形外；5的位置属性与网格点(1,2)的位置属性相同，位于多边形内。

2 复杂度分析

根据文献[1]对网格中心点算法的分析，网格单元数的复杂度为()，空间复杂度为()。由于本文方法采用与其相同的公式确定网格分辨率，而在预处理过程中仅为每个网格交点增加了一个bit位记录其位置属性，且增加了()个字节存储多边形边与网格边的交点，因此本文方法的空间复杂度仍为()。

本文方法的预处理过程如下：

(1) 创建均匀网格。本文方法与文献[1]采用相同的公式确定网格分辨率，时间复杂度为()。

(2) 计算网格线与多边形边的交点坐标，并将其存储到相应的数组中。由于一条边一般只与数个网格单元相交，检测条边，其时间复杂度为()。

(3) 将所有的多边形边片段加入到对应的网格单元中，类似文献[10]，时间复杂度为()。

(4) 确定网格交点的位置属性。对于每个网格交点，只需检测其临近网格点的位置属性和查询其之间网格边对应的交点数目即可，时间复杂度为()。

本文方法的判定计算过程如下：

(1) 被测点位于无边的网格内。被测点与临近网格顶点具有相同的属性，时间复杂度为(1)。

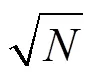
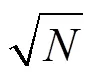
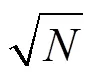
虽然本文方法与文献[1]具有相同的时间复杂度，但本文方法通过形成平行坐标轴的测试线、记录多边形位于各个网格单元中的边片段，由此可基于一些简单计算，大幅提高测试线与多边形的边的求交计算效率。

3 实验与讨论

本文在一台微机上进行了算法实现，该微机的硬件环境为Intel(R) Core(TM) i7-8700 CPU @ 3.20 GHz，16 GB ARM，软件开发环境为MS Windows 10操作系统，visual studio 2017。近年来，点在多边形内判定算法的研究不多且进展缓慢，其中较好的算法有凸剖分法[8]、CBCA[10]和QCPM[11]等，这些方法在文献[1]中均有对比分析。由于本文方法是在文献[1]的基础上进行改进，且上述方法在性能方面均次于文献[1]方法，因此，本文方法仅与文献[1]方法进行对比实验。测试用例来自文献[10]，如图6所示。测试用点1000×1000个，其均匀分布在比多边形包围盒稍大的范围内。

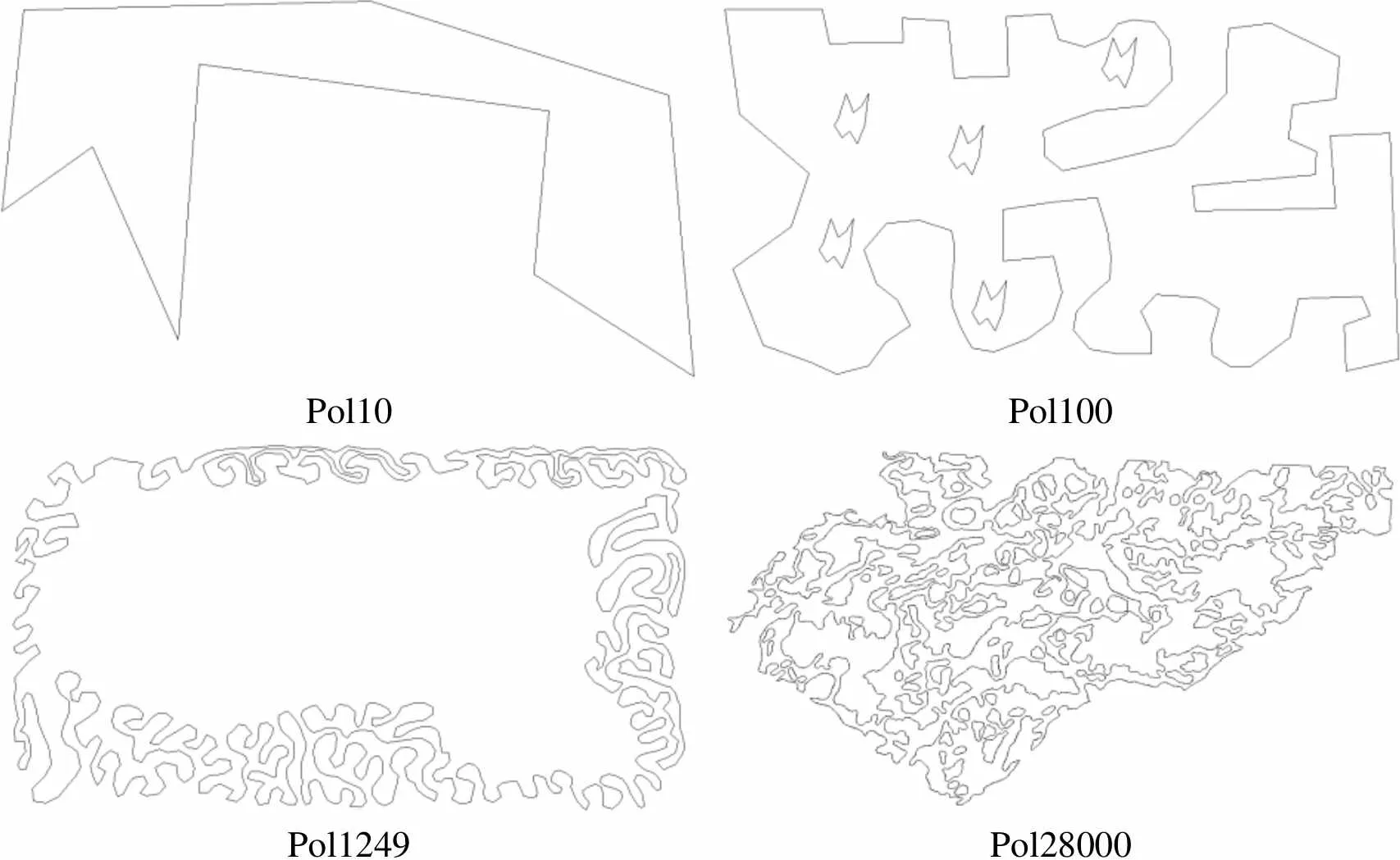
Pol10Pol100 Pol1249Pol28000

实验统计数据见表1，其中，判定时间为检测所有测试点的总时间。由表1可知，由于本文方法需要计算多边形边与网格边的交点，并对这些交点进行排序和存储，因此在预处理阶段本文方法耗费了更多时间。但在判定计算过程中，相较于网格中心点算法[1]，本文方法的效率提升了2倍多，且随着多边形的边数增多、复杂性的增大，本文方法的加速更多。

表1 新算法与网格中心点算法的对比实验数据

多边形边数网格分辨率算法预处理时间(加速率rp)# (ms)判定时间(加速率rd)^ (ms) Pol10108×6网格中心点算法0.33331.965 本文新算法0.339 (–0.017 70)15.199 (1.103 10) Pol10010038×18网格中心点算法0.40929.036 本文新算法1.422 (–0.712 38)12.747 (1.277 87) Pol12491 249100×46网格中心点算法0.90026.064 本文新算法9.889 (–0.908 99)12.918 (1.017 65) Pol2800028 000100×100网格中心点算法4.73484.590 本文新算法195.272 (–0.975 76)24.913 (2.395 42)

(注：# r=(T–T)/T，T为网格中心点算法的预处理时间；T为新算法的预处理时间；^ r=(T−T)/T，T为网格中心点算法的判定计算时间；T为新算法的判定计算时间)

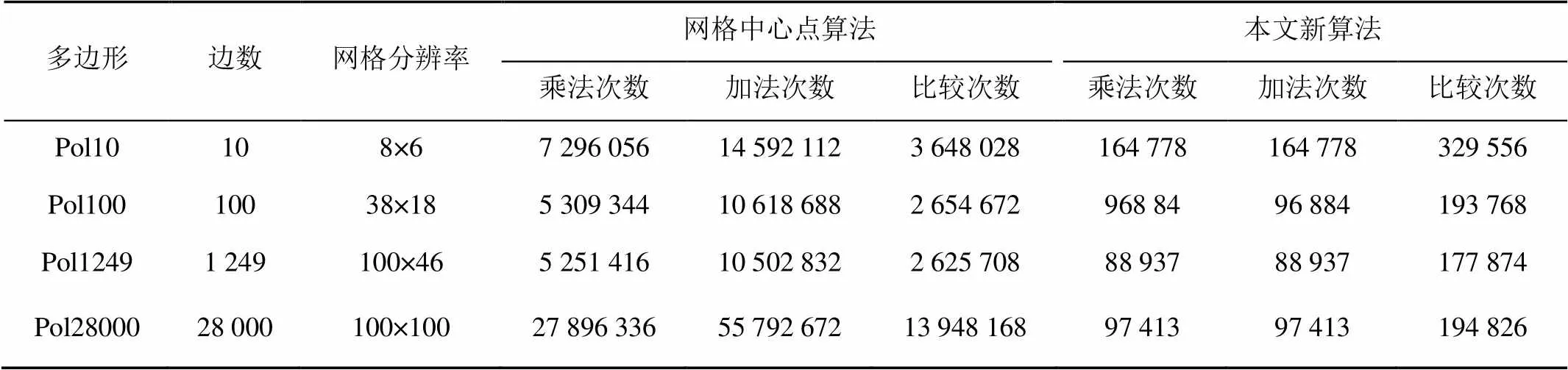
表2 新算法与网格中心点算法的数值计算次数的对比实验数据

多边形边数网格分辨率网格中心点算法本文新算法 乘法次数加法次数比较次数乘法次数加法次数比较次数 Pol10108×67 296 05614 592 1123 648 028164 778164 778329 556 Pol10010038×185 309 34410 618 6882 654 672968 8496 884193 768 Pol12491 249100×465 251 41610 502 8322 625 70888 93788 937177 874 Pol2800028 000100×10027 896 33655 792 67213 948 16897 41397 413194 826

为了进一步分析本文方法加速的原因，本文针对网格中心点算法和本文方法的判定计算过程的数值计算次数进行了统计分析，即测试边与多边形边的求交过程的计算量，实验结果见表2，其中，乘法次数和加法次数分别代表测试边与多边形边在求交过程中需要进行乘法运算和加法运算的次数。对于比较次数，在网格中心点算法中，主要是比较叉积值与0值的次数，而在本文算法中，主要是比较测试边和多边形边交点坐标值与测试边坐标值的次数。如第1.1.2节中所述，网格中心点算法中计算两条斜边是否相交需要4次叉积运算和4次比较运算，即需要进行16次加法和8次乘法，而本文方法在一次求交过程中只需要1次乘法、1次加法和2次比较。从表2可看出，在确定网格分辨率和测试点的情况下，本文方法所需的乘法计算和加法计算次数明显低于网格中心点算法所需的计算次数，同时，本文方法所需的比较次数也明显低于网格中心点算法所需的比较次数。

4 结束语

本文提出一种新的基于均匀网格的点在多边形内的判定算法。通过加强简便计算的处理，很好地减少测试线与多边形边的求交计算开销，提高了射线法局部化实现的效率。实验表明，相比目前最快的类似算法，可将测试计算的效率提高2倍多，且多边形的边越多越复杂，加速性能越高。

[1] 李静, 王文成. 基于网格中心点的点在多边形内的高效判定[J]. 软件学报, 2012, 23(9): 2481-2488.

[2] HUGHES J F, VAN DAM A, FOLEY J D, et al. Computer graphics: Principles and practice [M]. New Jersey: Pearson Education, 2014: 81-98.

[3] FEITO F, TORRES J C, UREÑA A. Orientation, simplicity, and inclusion test for planar polygons [J]. Mathematical Gazette, 1995, 19(4): 595-600.

[4] FEITO F R, TORRES J C. Inclusion test for general polyhedral [J]. Computers and Graphics, 1997, 21(1): 23-30.

[5] 张宏, 温永宁, 刘爱利. 地理信息系统算法基础[M]. 北京: 科学出版社, 2006: 25-28.

[6] BERG M, CHEONG O, KREVELD M, et al. Computational geometry: Algorithms and applications [M]. Berlin: Springer-Verlag, 2008: 121-144.

[7] ZALIK B, CLAPWORTHY G J. A universal trapezoidation algorithm for planar polygons [J]. Computers and Graphics, 1999, 23(3): 353-363.

[8] LI J, WANG W C, WU E H. Point-in-polygon tests by convex decomposition [J]. Computers and Graphics, 2007, 31(4): 636-648.

[9] JIMÉNEZ J J, FEITO F R, SEGURA R J. A new hierarchical triangle-based point-in-polygon data structure [J]. Computers and Geoscienes, 2009, 35(9): 1843-1853.

[10] ZALIK B, KOLINGEROVA I. A cell-based point-in-polygon algorithm suitable for large sets of points [J]. Computers and Geosciences, 2001, 27(10): 1135-1145.

[11] YANG S, YONG J H, SUN J, et al. A point-in-polygon method based on a quasi-closest point [J]. Computers and Geosciences, 2010, 36(2): 205-213.

[12] WANG W C, LI J, WU E H. 2D point-in-polygon test by classifying edges into layers [J]. Computers and Graphics, 2005, 29(3): 427-439.

[13] 李楠, 肖克炎. 一种改进的点在多边形内外判断算法[J]. 计算机工程, 2012, 38(5): 30-34.

[14] 孙爱玲, 赵光华, 赵敏华, 等. 基于sign(x)函数的点在多边形内外判别算法及应用[J]. 计算机工程与科学, 2017, 39(4): 785-790.

[15] CLEARY J G, GEOFF W. Analysis of an algorithm for fast ray tracing using uniform space subdivision [J]. Visual Computer, 1988, 4(2): 65-83.

[16] LI J, WANG W C. Fast and robust GPU-based point-in-polyhedron determination [J]. Computer-Aided Design, 2017, 87: 20-28.

Efficient Point-in-Polygon Tests with Local and Simple Computation

WANG Sheng-chun1,2, WANG Wen-cheng1,2, TAN Xue-han1,2, LI Jing3

(1. State Key Laboratory of Computer Science, Institute of Software, The Chinese Academy of Sciences, Beijing 100190, China; 2. School of Computer Science and Technology, University of Chinese Academy of Sciences, Beijing 100190, China; 3. Key Laboratory of Zoological Systematics and Evolution, Institute of Zoology, Chinese Academy of Sciences, Beijing 100101, China)

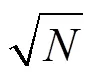
polygon; grid; simple computation; point-in-polygon tests

TP 391

10.11996/JG.j.2095-302X.2019020267

A

2095-302X(2019)02-0267-07

2018-09-01；

2018-09-18

国家重点研发计划项目(2017YFB1002700)；国家自然科学基金项目(61661146002，61872348)

王盛春(1991-)，男，陕西延安人，博士研究生。主要研究方向为计算机图形学、纹理分析等。E-mail：wangsc@ios.ac.cn

王文成(1967-)，男，湖南双峰人，研究员，博士，博士生导师。主要研究方向为计算机图形学、虚拟现实及可视分析等。 E-mail：whn@ios.ac.cn