带形状参数的R-Coons曲面
2019-05-14韩旭里
邹 倩,韩旭里
带形状参数的R-Coons曲面
邹 倩1,2,韩旭里2
(1. 淮北师范大学信息学院,安徽 淮北 235000;2.中南大学数学与统计学院,湖南 长沙 410083)
为了解决传统Coons曲面不具备形状可调性,不能精确表示椭球面、椭圆锥面、椭圆柱面等二次曲面的问题,在有理函数空间上构造了一组有理混合基函数,称之为R-Hermite基。首先分析了R-Hermite基的性质;其次基于R-Hermite基,利用张量积方法,构造了一种新的带两个形状参数的有理Coons曲面,并称之为R-Coons曲面,R-Coons曲面不仅具有传统Coons曲面的良好性质,还具备形状可调性;最后给出了曲面精确表示椭球面、椭圆锥面、椭圆柱面的方法,并通过实例说明方法的有效性。
R-Hermite基;R-Coons曲面;形状参数;椭圆锥面
曲线曲面构造是计算机辅助几何设计(computer aided geometric design,CAGD)领域的主要研究内容,所构造的曲线曲面是否具有形状可调性以及能否精确表示弧线、柱面曲线等曲线和椭球面(球面)、椭圆柱面(柱面)等二次曲面是衡量所构造曲线曲面好坏的重要标准之一。为了改进形状可调性的问题,许多学者在基函数中引入形状参数[1-5],文献[1]构造了带形状参数的高阶连续的保形有理插值曲线;文献[2]给出带形状参数的1有理二次三角多项式曲线;文献[3]构造了含3个形状参数的五次多项式基函数;文献[4]构造了具有保形性的三次均匀B-样条扩展曲线,并加入了形状参数。

1 R-Hermite基及其性质
1.1 R-Hermite基的构造
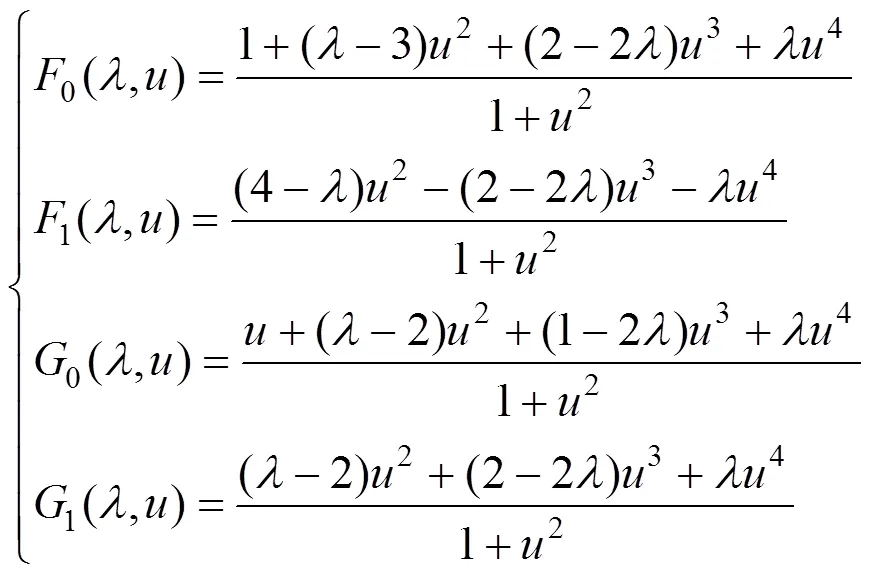
1.2 R-Hermite基的性质
性质1.端点性质。可以验证
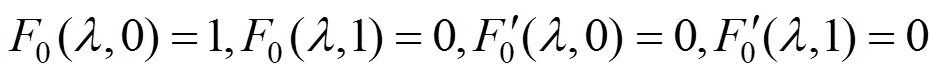
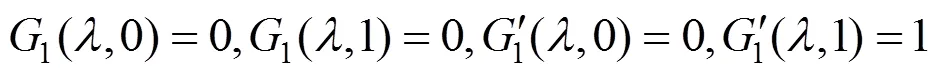
故R-Hermite基具有类似于Hermite基的端点性质

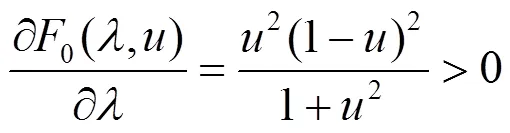
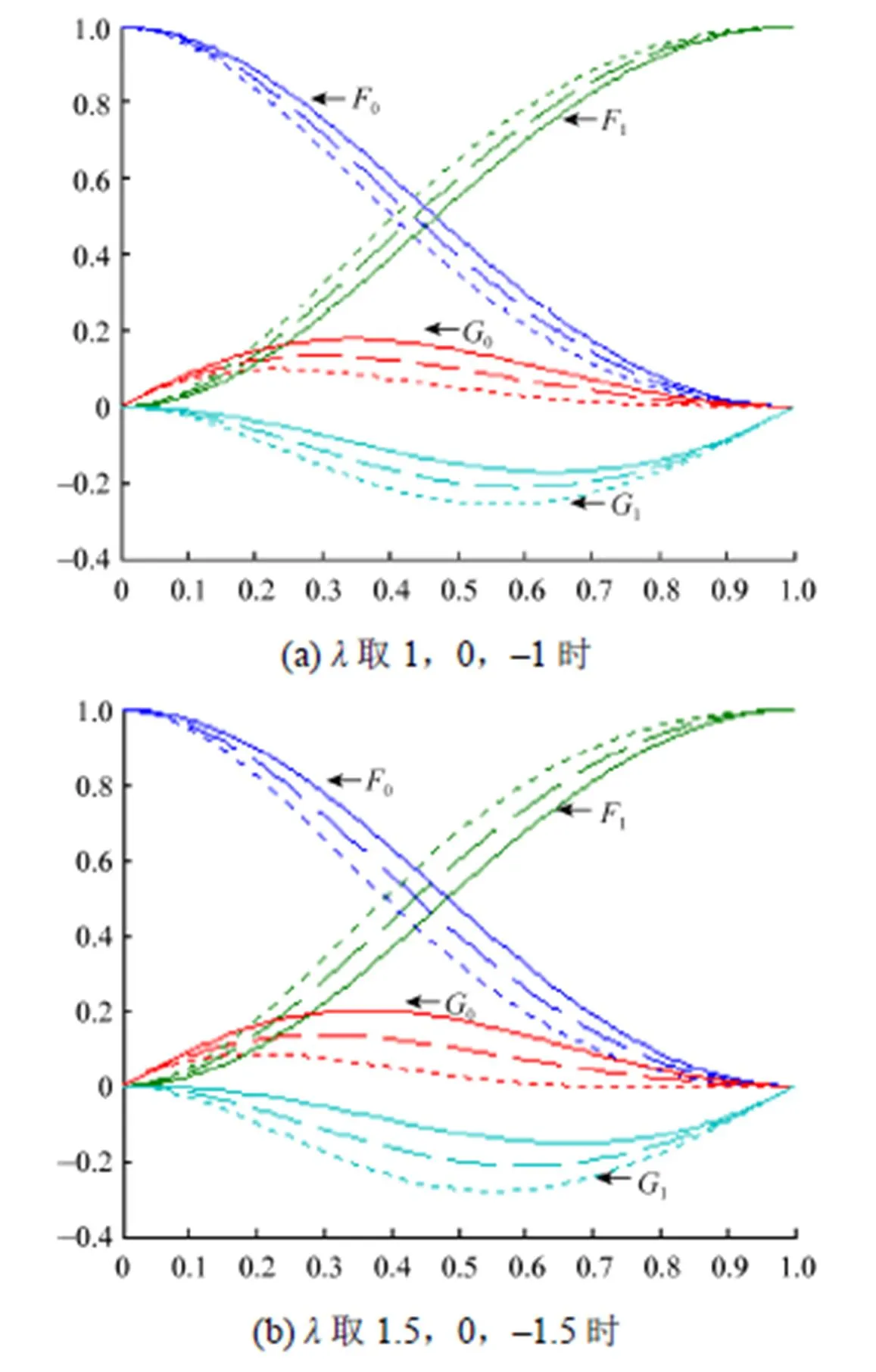
图1 λ取不同值时R-Hermite基的图形
2 R-Coons曲面
2.1 R-Coons曲面的构造
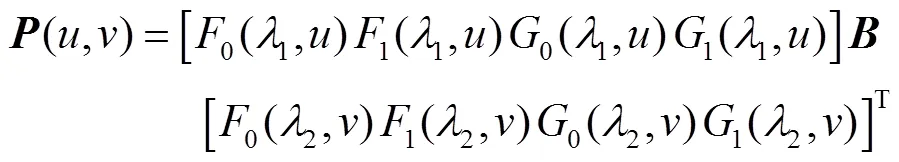
其中
式(1)可以改写为
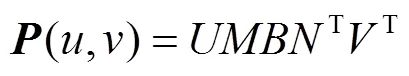
其中
曲面片式(2)对应的参数方程为
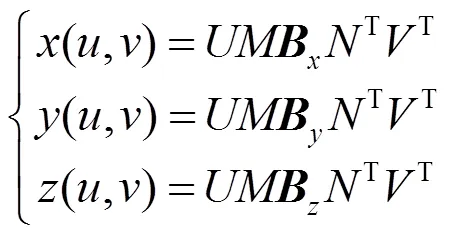
其中,,,分别为信息矩阵的坐标分量矩阵。
2.2 R-Coons曲面的性质
性质1.插值性。R-Coons曲面插值于4个角点(,),且,=0.1,4个角点处的切矢p(,),p(,),,=0.1和4个扭矢p(,),,=0.1。
性质3.几何不变性。由于R-Coons曲面和双三次Coons曲面类似,是利用参数化构造方法,所以曲面的形状和位置与坐标系的选择无关。
3 R-Coons曲面片实例
例1.取边界信息矩阵
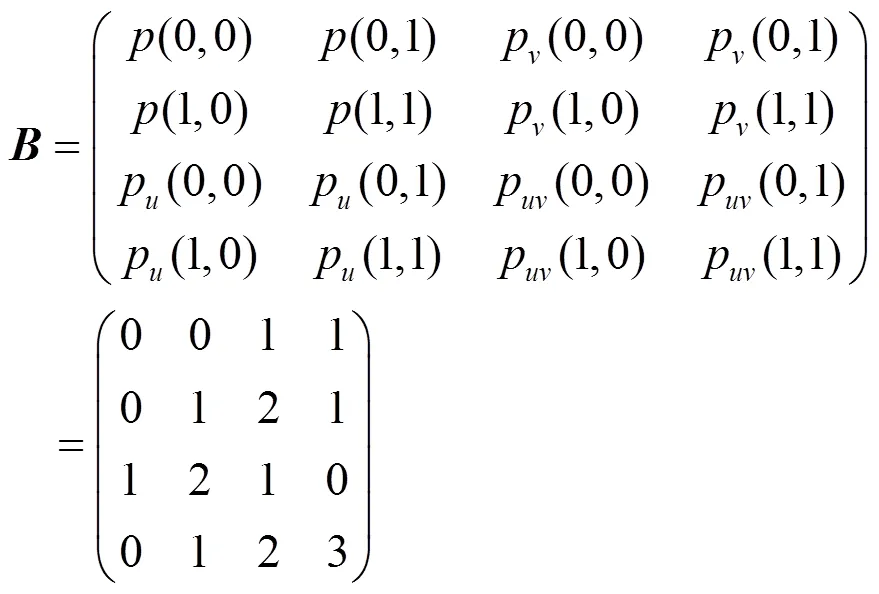
当形状参数和取不同值时,可以得到不同的曲面片(图2)。
例2.取边界信息矩阵

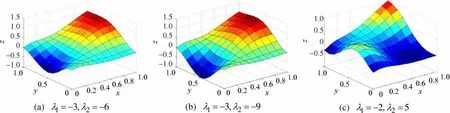
(a) (b) (c)
4 R-Coons曲面在几何造型上的应用
4.1 椭球面(球面)
椭球面的一种参数方程为
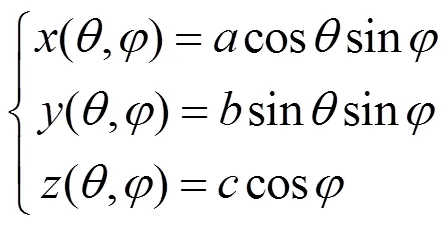
对于第2节定义的R-Coons曲面,给出边界信息矩阵的坐标分量如下
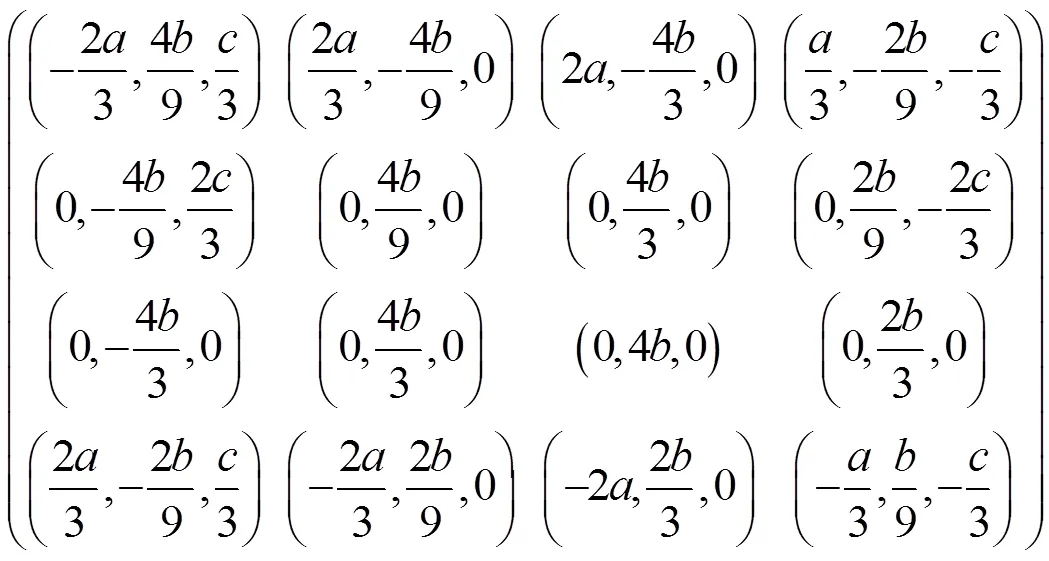
显然,式(4)表示部分椭球面,图4是=5,=6,=8时曲面的图形。当==>0时,式(4)为部分球面,图5是===5时曲面的图形。
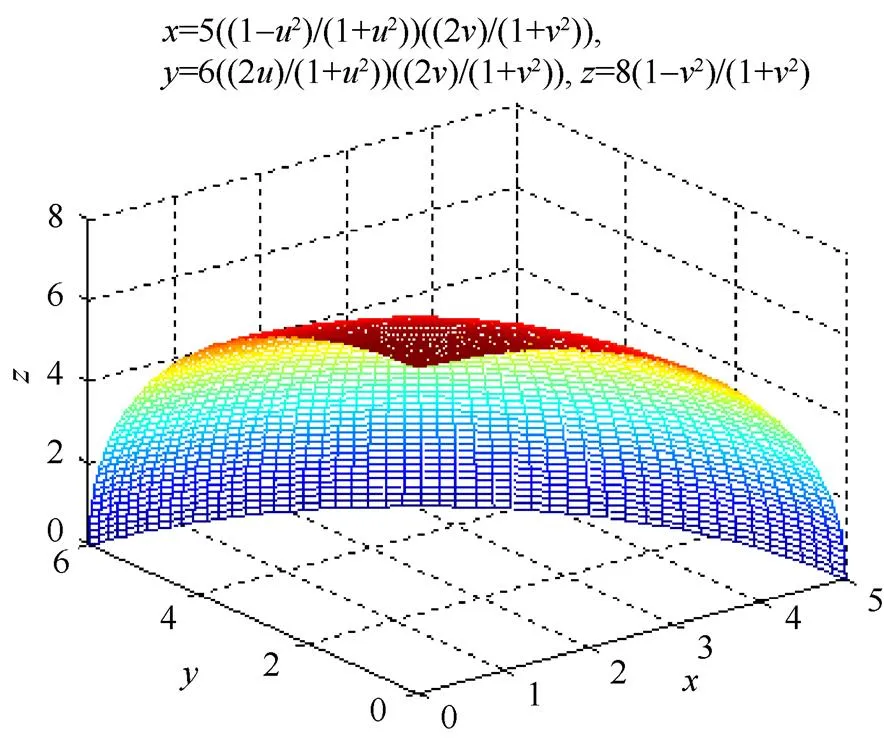
图4 部分椭球面

图5 部分球面
4.2 椭圆锥面(圆锥面)
椭圆锥面的一种参数方程为

对于第2节定义的R-Coons曲面,给出边界信息矩阵的坐标分量如下

(5)
式(5)为部分椭圆锥面,图6是=2,=4,=6时曲面的图形,当=时,式(5)为圆锥面,图7是===3时曲面的图形。
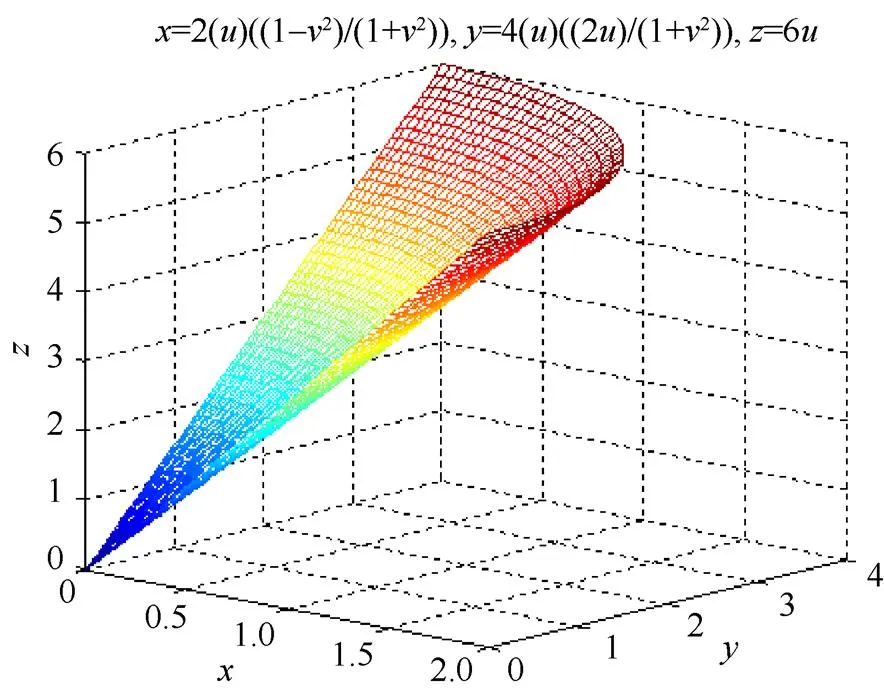
图6 部分椭圆锥面
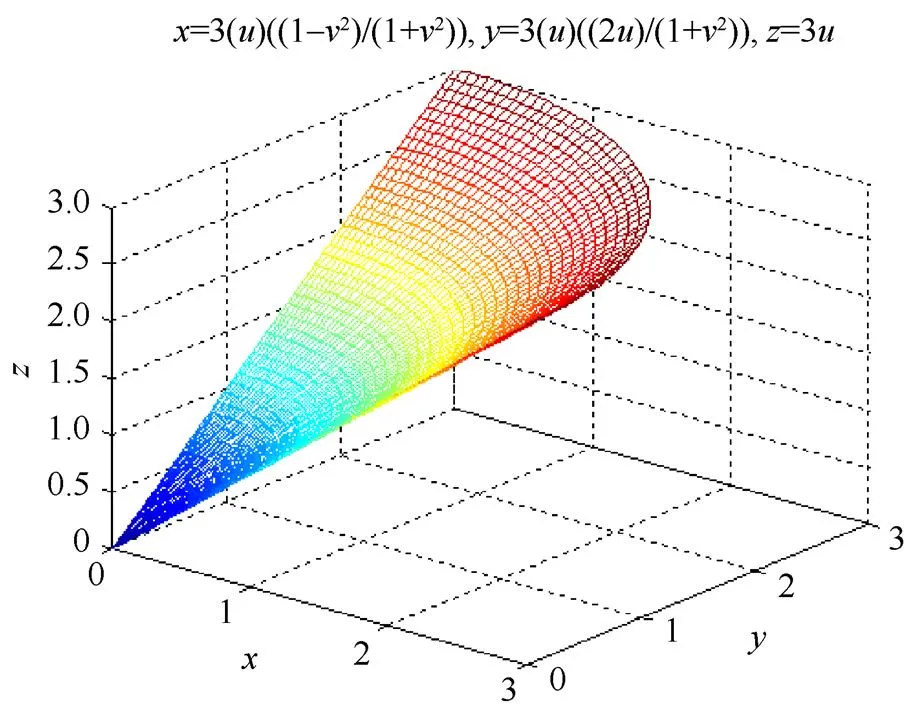
图7 部分圆锥面
4.3 椭圆柱面(圆柱面)
椭圆柱面的一种参数方程为
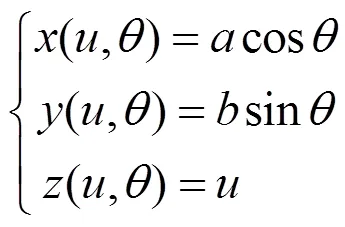
对于第2节定义的R-Coons曲面,给出边界信息矩阵的坐标分量如下
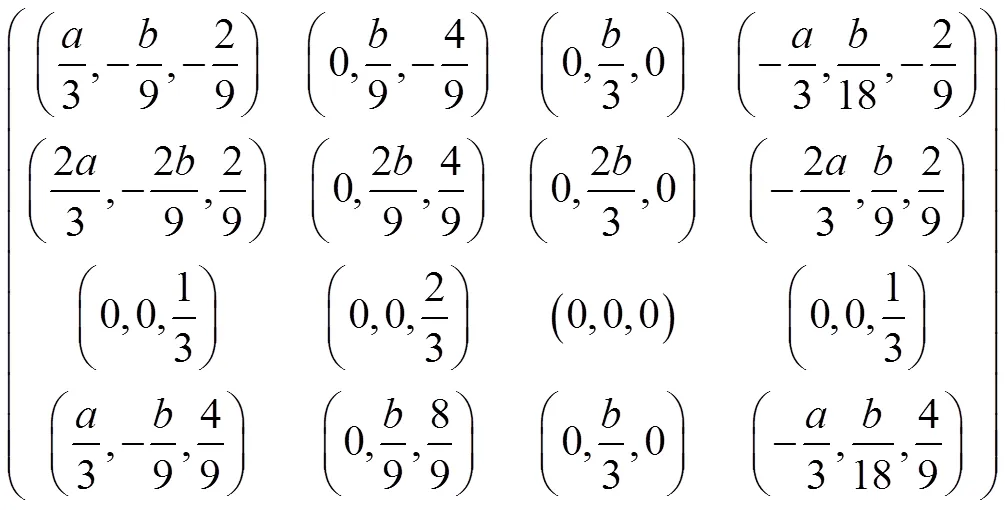
(6)
式(6)表示的为部分椭圆柱面,图8是=3,=5时曲面的图形,当=时,式(6)为圆柱面,图9是==3时曲面的图形。
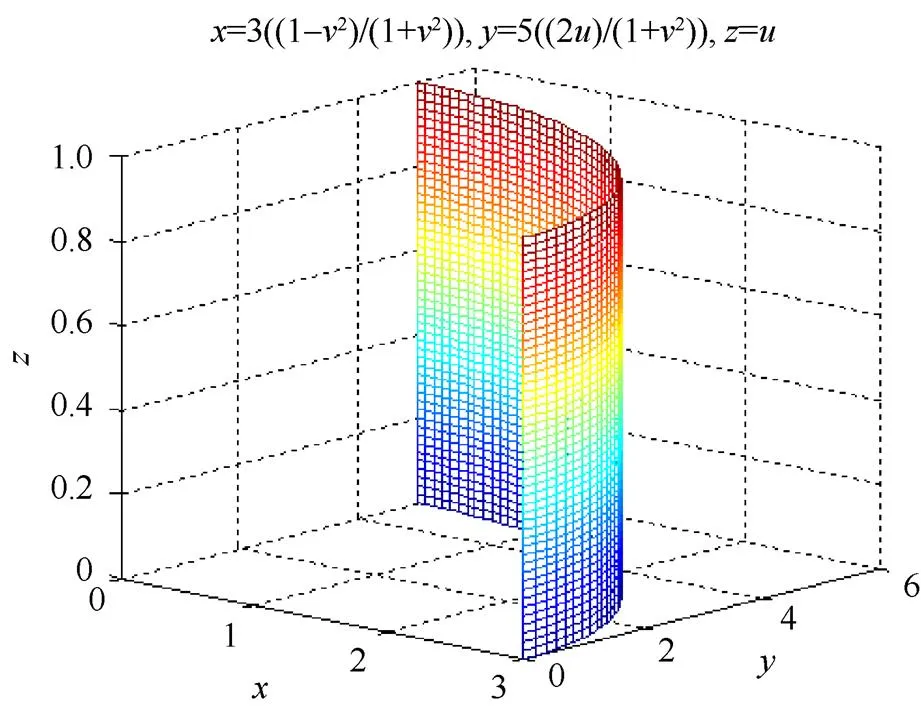
图8 部分椭圆柱面
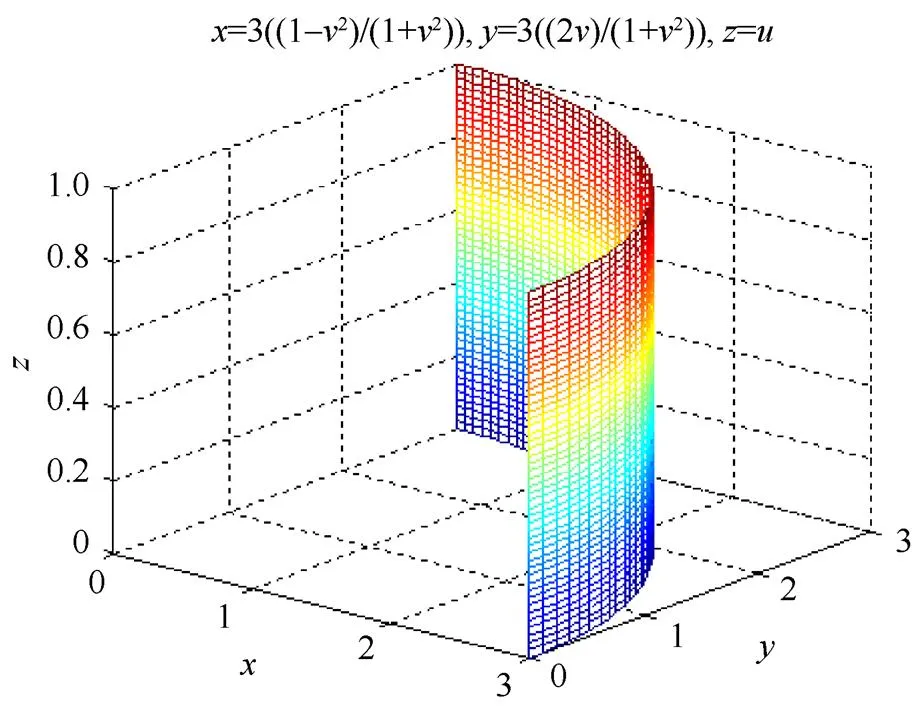
图9 部分圆柱面
5 结束语

[1] HAN X L. Shape-preserving piecewise rational interpolation with higher order continuity [J]. Applied Mathematics and Computation, 2018, 337: 1-13.
[3] 仇茹, 杭后俊, 潘俊超. 带三参数的类四次Bezier曲线及其应用研究[J]. 计算机工程与应用, 2014, 50(20): 158-162.
[4] 严兰兰, 韩旭里. 基于全正基的三次均匀B样条曲线的扩展[J]. 图学学报, 2016, 37(3): 329-336.
[5] 尹池江, 檀结庆. 带多形状参数的三角多项式均匀B样条曲线曲面[J]. 计算机辅助设计与图形学学报, 2011, 23(7): 1131-1138.
[6] 朱心雄. 自由曲线曲面造型技术[M]. 北京: 科学出版社, 2002: 57-65.
[7] WANG Y, TAN J, LI Z, et al. Bi-cubic C-Coons surface and its applications [J]. Journal of Information and Computational Science, 2012, 9(7): 1895-1903.
[8] 裴芳, 韩旭里, 李岩. 带形状参数的Coons类曲面的构造与拼接[J]. 计算机工程与应用, 2013, 49(10): 163-166.
[9] 王晶昕, 董莹, 倪静. 带调节参数的双二阶三角多项式Coons曲面片[J]. 大连交通大学学报, 2013, 34(1): 110-112.
[10] 李杨, 汤文成, 刘海晨. C-Coons曲面及其性质[J]. 计算机辅助设计与图形学学报, 2003, 15(9): 1177-1180.
[11] 邹倩, 韩旭里, 包崇兵. 两种带形状参数的有理Coons曲面[J]. 工程图学学报, 2009, 30(6): 71-75.
[12] 李军成, 杨炼, 李炳君. 双三次Coons曲面片的两种扩展[J]. 计算机应用研究, 2011, 28(11): 4389-4391.
[13] 李军成, 赵东标, 陆永华. 带参数有理Coons曲面插值的图像缩放方法[J]. 计算机辅助设计与图形学学报, 2011, 23(11): 1853-1859.
[14] LES P, TILLER W. 非均匀有理B样条[M]. 赵罡, 穆国旺, 王拉柱, 译. 北京: 清华大学出版社, 2010: 7-30.
R-Coons Surface with Shape Parameters
ZOU Qian1,2, HAN Xu-li2
(1. College of Information, Huaibei Normal University, Huaibei Anhui 235000, China; 2. School of Mathematics and Statistics, Central South University, Changsha Hunan 410083, China)
In order to solve the lack of shape adjustability of the traditional Coons surface and the inability to accurately represent ellipsoid, elliptical cone, and elliptical cylinder etc., a set of rational hybrid basis functions is constructed in rational space, which is named R-Hermite basis. Firstly, the properties of R-Hermite basis are illustrated. Secondly, based on the R-Hermite basis, a rational Coons surface with two shape parameters is constructed by using the tensor product method, and it is called R-Coons surface, which not only has the good properties of traditional Coons surface, but also has shape adjustability. Finally, the method that can accurately represent ellipsoid, elliptical cone and elliptical cylinder is given, and some examples are illustrated to prove the effectiveness of the method.
R-Hermite basis; R-Coons surface; shape parameter; elliptical cone
TP 391.72
10.11996/JG.j.2095-302X.2019020388
A
2095-302X(2019)02-0388-07
2018-08-03;
2018-10-20
国家自然科学基金项目(11771453);安徽省自然科学研究项目(KJ2017A849)
邹 倩(1984-),女,安徽怀远人,讲师,硕士。主要研究方向为计算机辅助几何设计、几何造型等。E-mail:zouqian7@163.com
