高雷诺数流动模拟的LBM方法

陈彦晓,李孝伟,丁 珏,翁培奋

(上海大学上海市应用数学和力学研究所,上海200072)

格子Boltzmann方法(lattice Boltzmann method,LBM)是一种从介观角度出发对流动进行数值模拟的方法,在过去的几十年里已经发展得相对成熟[1].传统的LBM方法建立在均匀的网格上,故也称为标准的LBM方法,该方法要求在每一个时间步长上,微粒从一个格点严格运动到其相邻的另一个格点[2].格子Boltzmann方法使用标准均匀网格,具有原理简单、实施方便且并行性能好等优点[3],但也存在计算精度不可调、复杂边界处理困难等缺点.

为了避免标准LBM方法中均匀网格的缺陷,国内外学者提出了许多改进方法[4].这些方法主要分为两种:第一种是采用分区网格或自适应直角网格[5],在需要高精度求解的局部区域直接建立或通过自适应技术构造细化的直角网格,该办法能够有效地解决计算精度不可调的问题,主要优势在于每个网格的运算法则与标准的LBM完全相同,只是在非均匀网格交界面上通过插值进行必要的数值传递;第二种是采用贴体网格.将贴体网格用于LBM方法较好地解决了曲面边界和网格加密的问题,由此也产生了一种补充插值LBM(interpolation supplemented LBM,ISLBM)方法[6].Imamura等[7]在此基础上又发展出了一种广义形式补充插值LBM(generalized interpolation LBM,GILBM),可以适用于更一般的几何外形.1997年He等[8]首次使用GILBM方法对圆柱绕流进行了模拟计算,结果证明:该方法在Re<104的亚临界区内具有较好的数值稳定性;而当雷诺数进一步提高时,数值计算容易失稳.为了改善LBM方法处理实际问题时受高雷诺数限制的缺陷,有研究人员提出采用多松弛时间模式的LBM方法[9].研究表明,多松弛时间模式对算法的计算稳定性有一定的改进,但所能模拟的最大雷诺数仅扩大4倍.

基于此,本工作发展了一种在贴体网格GILBM框架下的当地时间步改进方法,该方法是基于传统当地时间步法[10]发展起来的,通过结合分子运动论[11]的相关原理,使计算域内各点都可以采用满足该点CFL条件所允许的最大时间步长.本工作对高雷诺数下NACA0012翼型绕流的数值模拟表明,采用当地时间步改进方法可以改善高雷诺数流动模拟的计算稳定性,并有效地提高了计算效率.

1 标准LBM

格子Boltzmann采用了微观尺度上的Boltzmann方程,在BGK近似中引入了碰撞算子(Maxwell-Boltzmann分布函数),

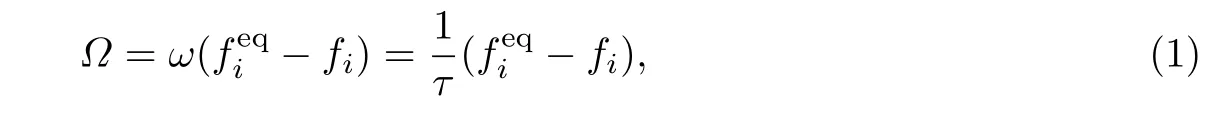
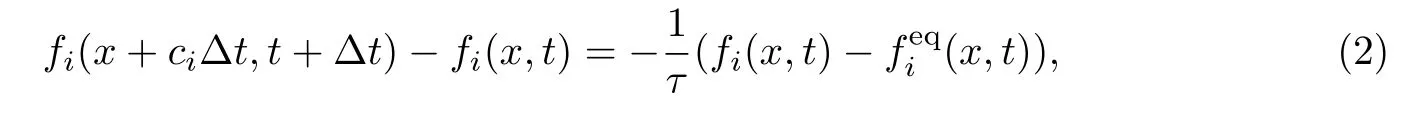
式中,∆t为时间步长.格子Boltzmann方法控制方程可以分为两部分:碰撞和迁移.碰撞是指不同速度的粒子在到达同一格点时将依据BGK碰撞模型的法则,改变自己的分布函数.迁移是指粒子碰撞后将按固定的速度运动到最近的节点,其粒子分布函数也会随之运动.因此,格子Boltzmann方法控制方程的演化方程分为两部分:碰撞项和迁移项.

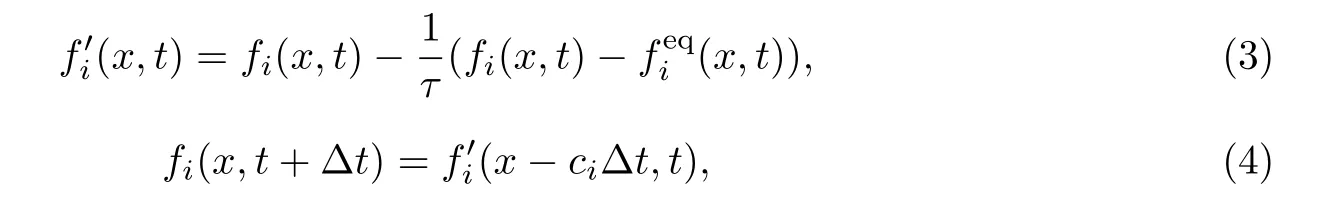
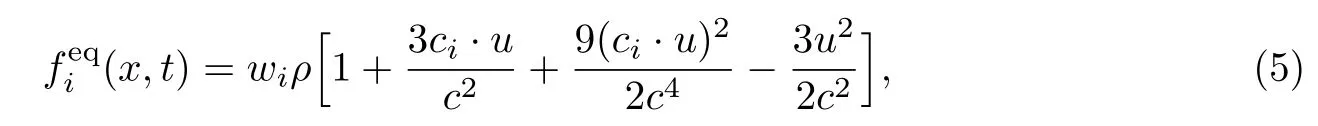
式中,w0=4/9,w1=w2=w3=w4=1/9,w5=w6=w7=w8=1/36,

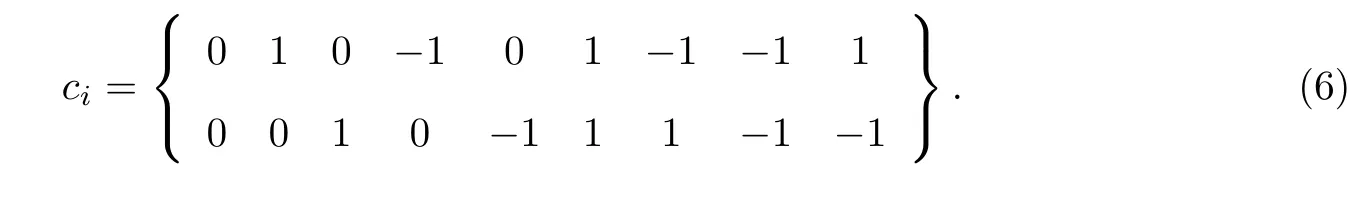
宏观变量可以通过分布函数fi描述,其中密度ρ和速度u分别为

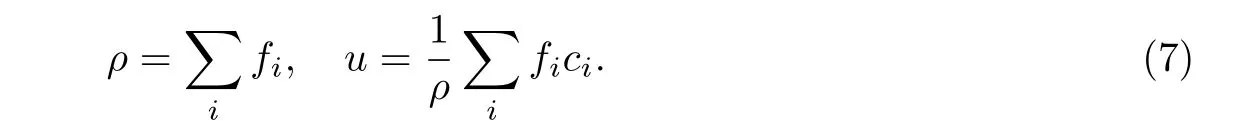
通过式(7)可求得压强为

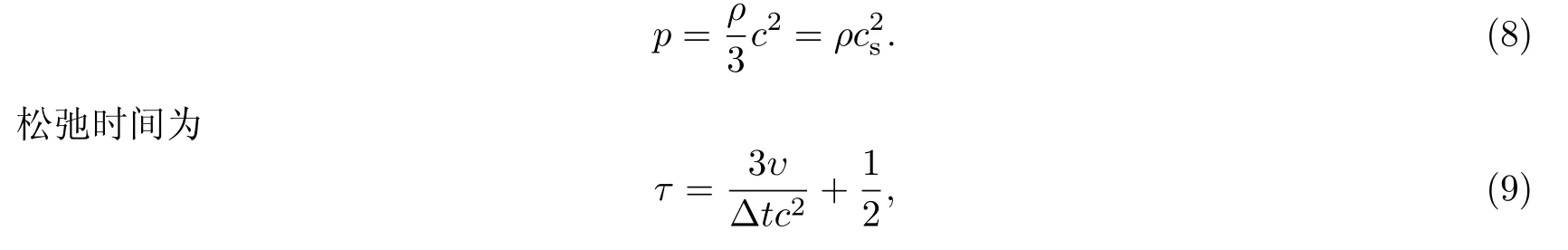
式中,运动黏度υ和雷诺数相关,即

其中U0为远场速度,L为特征速度.

2 GILBM

GILBM是基于ISLBM思想的广义坐标下的LBM模型.借鉴传统计算流体力学中的方法,引入计算区域的概念.物理区域上的坐标点(x,y)对应于计算区域上的点(ξ,η).物理平面上是贴体网格,而计算平面上的网格是均匀直角网格.网格间隔∆ξ,∆η一般均取1.

在物理平面上,离散速度是常矢量,但在计算平面上格点的离散速度随位置变化而变化,为变矢量.将计算平面上格点的离散速度记为ei,∂(∂=0,1),根据计算平面与物理平面的关系,可以得出离散速度在物理域和计算域的转换关系.

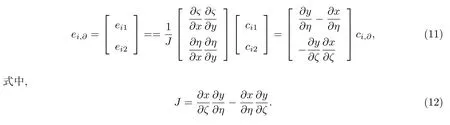
求得迁移运动速度在计算平面上的分量后,通过对ei,∂在时间步长的积分

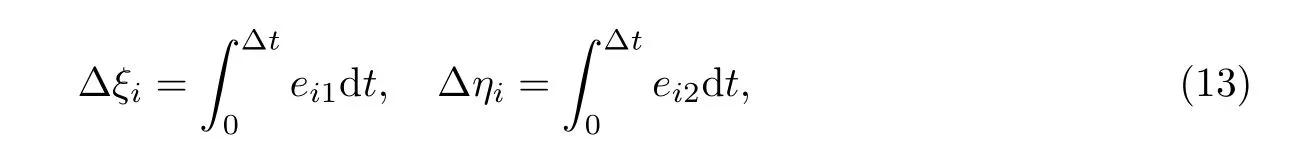
得到物理平面上碰撞后粒子在计算平面相应的位置.由于该位置一般并不位于网格格点上,因此可以通过距离该点最近的网格节点上的分布函数插值得到该点上的分布函数数值.

虽然可以选择不同的插值格式进行计算,但为了避免虚假的线性速度,线性插值的数值精度是远远不够的.为了在保证计算精度的前提下力求计算稳定,在流场内部区域节点采用二阶迎风插值,因此碰撞后粒子的分布函数为

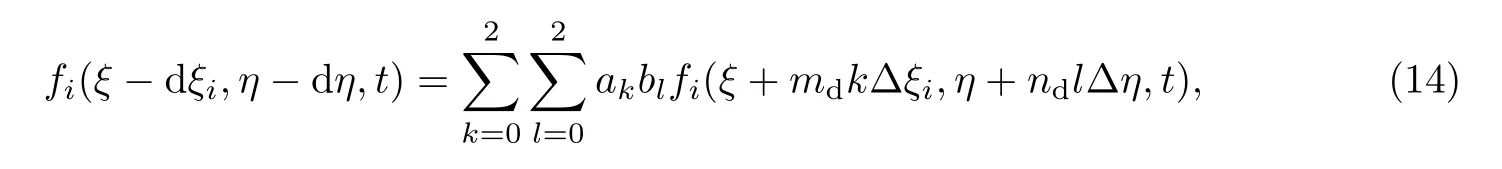
式中,ak,bl,sk,dl(k,l=−1,0,1,2)为插值系数,md=sgn(dξ),nd=sgn(dη)用来确定插值过程中插值点的取值方向.对于与边界相邻的网格节点,由于网格节点数目的限制,无法使用二阶迎风插值,本工作采用二阶中心插值求解,碰撞后粒子的分布函数为

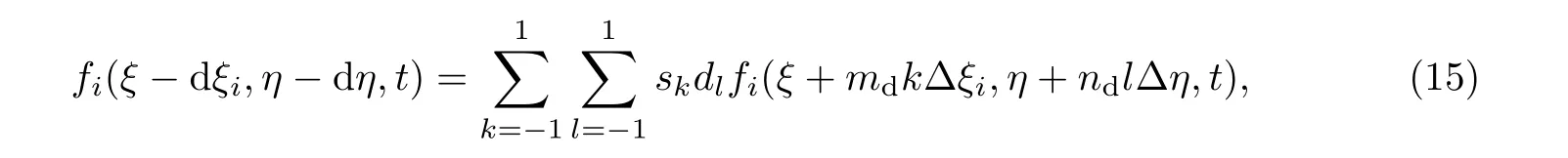
3 边界条件

与传统的计算流体力学方法相同,在使用格子Boltzmann方法进行流场模拟分析时,边界的处理对计算结果的精度、计算的数值稳定性以及计算效率都有很大影响.研究表明,非平衡态外推格式[12]在时间和空间上都具有二阶精度,而且该格式操作简单、数值稳定且适用范围广.因此,本工作采用非平衡态外推格式作为计算过程中的边界处理方法.实施过程为

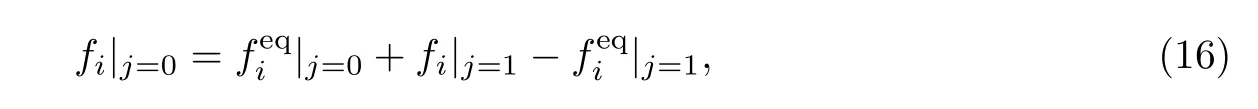
4 当地时间步改进技术

LBM作为一种介观模拟方法,与采用相同数量网格数的传统NS方程求解器相比,其计算时间要长的多,这是因为其时间推进方法为显示格式,会受到稳定性条件的限制.只有当时间步取整个流场允许的最小值时,才能满足时间精确度.如果被用来处理宏观问题,即较大雷诺数时,根据公式Re=U0L/υ可知,要么增大特征长度L,要么减小运动黏度υ.当L固定,只能使υ取非常小的值.由式(9)可知,LBM控制方程碰撞项线性化处理后,使得松弛时间τ取定值,如果υ值变小,则时间步也应变得更小,这就引起了数值计算的不稳定问题.

为保证数值迭代的稳定性,时间步长∆t需满足柯朗-弗里德里希斯-列维(Courant-Friedrichs-Lewy,CFL)条件,目的首先是为了保证数值精度,其次在计算区域内粒子每次的迁移距离不会超越一个格子.参照传统计算流体力学中的处理方法,全局性时间步为

式中:λ为CFL数,0<λ 6 1;min{1/c(i,j)}遍取计算平面所有的格点上离散速度的值.本工作引入当地时间步法,各点都可以采用该点稳定条件允许的最大时间步长,这样流场处处以稳定极限向前发展,计算速度明显提高.一般认为,引入当地时间步法可使计算时间减少一个量级.引入当地时间步法的时间步为

通过算例验证可知,在低雷诺数下引入当地时间步法可以显著提高计算效率,但是依然不能改善高雷诺数流动下计算不稳定的问题.为了解决这一问题,本工作结合分子运动论的相关原理,引入3个不同的时间尺度:碰撞时间∆t1=d/ξ、平均自由时间∆t2=l/ξ和宏观时间∆t3=L/ξ,其中d,l,L分别是气体分子的大小、平均自由程和宏观量变化尺度,ξ是气体分子平均运动速率.假设为考虑平均自由程的碰撞时间,则有

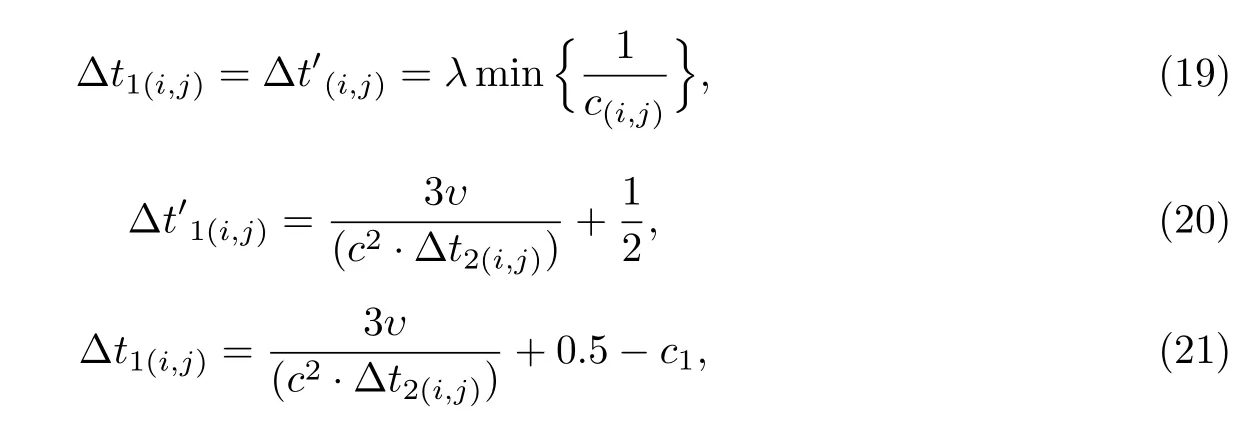
式中,c1=0.5.理论上,平均自由时间应等于分子平均自由程与分子运动特征速度之比.但在实际计算中,由于网格分辨率有限,迁移时间∆t2可以按式(19)来计算,式(21)即为只考虑两粒子接触时的碰撞时间.通过气体分子平均运动速率ξ,可得出碰撞时间∆t1(i,j)和平均自由时间∆t2(i,j)的关系为

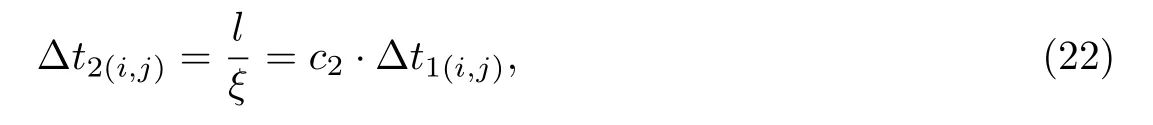
式中,c2=l/d>1.由于分布函数fi在∆t1(i,j)的时间间隔中变化很小,fi变化的时间尺度为∆t01(i,j).因此,为改善计算的收敛情况,可令时间步长随网格点不同自动调节,定义局部时间步长为

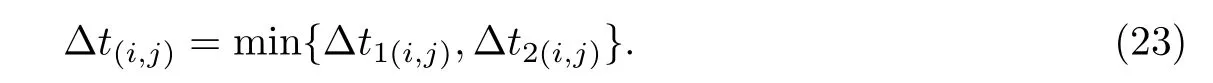
5 算例分析

NACA0012可认为是最简单的对称低速模型,近几十年来人们对它进行了大量的数值模拟[13]和风洞实验[14].本工作选择翼型绕流作为数值模拟的对象,主要目的有:①将采用当地时间步法的计算结果与试验值进行对比,检验算法在高雷诺数下的可靠性;②在不同雷诺数下对翼型绕流进行数值模拟,验证本工作中算法保持数值模拟稳定性的能力,同时检验算法的计算效率.

5.1 可靠性分析

为了检验算法的可靠性,本工作采用了Harris[15]的实验设置和实验数据,该实验是1981年在美国NASA Langley Research Center实验室3.0 m×9.0 m的跨声速风洞中进行的,实验来流马赫数Ma=0.3,模型弦长为0.635 m,雷诺数Re=3×106.Harris公布的实验数据含有不同攻角下翼型的升力系数值和翼型表面的压力系数,因此,可以将本工作计算的结果与Harris提供的实验数据进行对比.

计算模型采用304×90的C型网格,翼型上有128个点,最小网格(附面层第一层网格)尺度为8.6×10−5,翼型弦长为1.NACA0012流场计算网格如图1所示,其中x,y等相关物理量均为无量纲量,进口边界设在离翼型前缘10倍弦长处,出口边界为15倍弦长处.

表1是NACA0012翼型在不同攻角下的升力系数值.将本工作的计算结果和实验结果进行比较,可以看出:升力系数的变化规律是一致的,均随着攻角的增加而变大;计算值要比实验值偏高,这与本工作在计算中没有考虑湍流模型有一定关系.

图2为NACA0012翼型在−0.14◦,3.86◦和6.86◦攻角下吸力面和压力面压力系数分布曲线.由翼型表面压力系数Cp的分布可知,翼型上表面流动并没有发生流动分离,翼型下表面的压力系数与实验值吻合良好,而上表面的压力系数随着攻角增大会出现一定的误差.在未采用湍流模型的情况下,这样的计算精度是可以接受的.

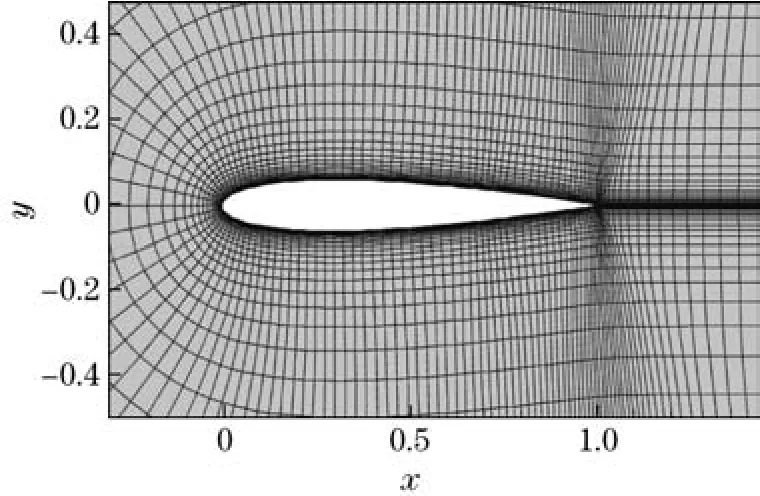
图1 NACA0012翼型流场的计算网格Fig.1 Calculation grid of flow around NACA0012

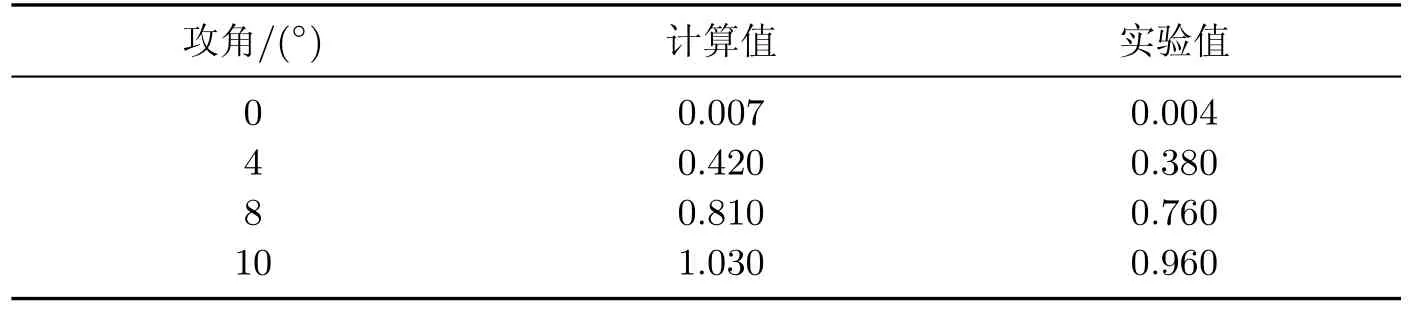
表1 NACA0012翼型不同攻角下的升力系数Table 1 Lift coefficient of NACA0012 airfoil at different angles of attack

图2 NACA0012翼型不同攻角下压力系数分布Fig.2 Pressure coefficient distribution of NACA0012 airfoil at different angles of attack

图3为8.86◦攻角时NACA0012翼型的流线图.由图可知,翼型绕流为附着流，在翼型上表面附近出现明显的附着涡结构,但未出现分离涡结构,但可以预见,随着翼型攻角的增大,附着涡会逐渐地变大,最后形成稳定的脱落涡结构.

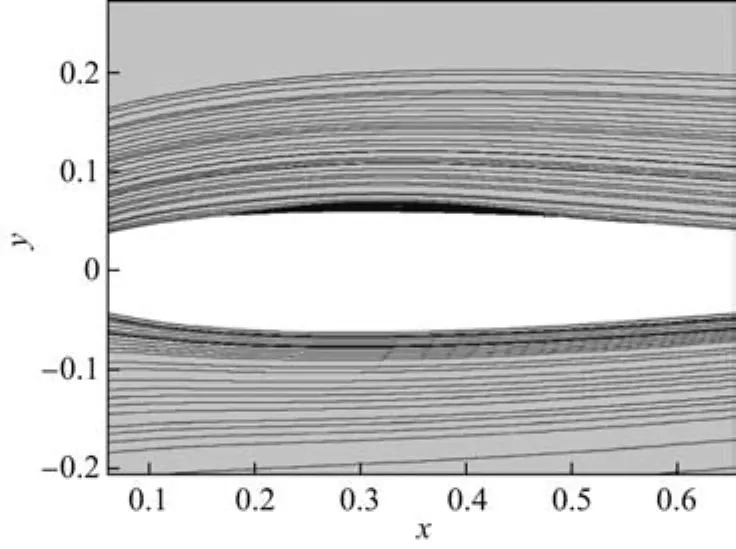
图3 NACA0012翼型8.86◦攻角时的流线图Fig.3 Streamline diagram of NACA0012 airfoil at 8.86◦angle of attack

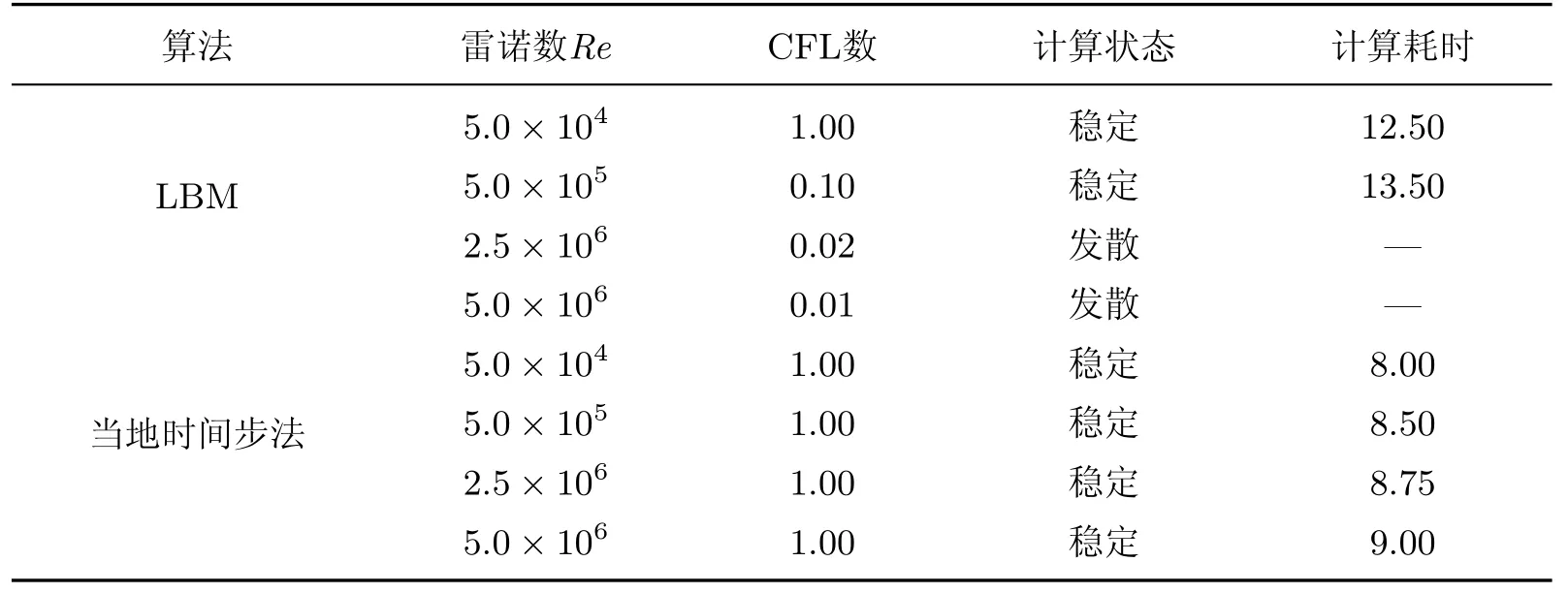
表2 雷诺数和CFL数不同时NACA翼型的计算状态参数Table 2 Calculation of state parameters for different Reynolds numbers and CFL numbers

5.2 计算效率和稳定性分析

为了进一步检验算法在高雷诺数下的适用性、计算效率和可靠性,本工作从算法改进前后计算状态均良好的中雷诺数出发,对不同中高雷诺数下的NACA0012翼型绕流进行了数值模拟,旨在发现雷诺数在增大至高雷诺数过程中计算状态的变化规律.取来流马赫数Ma=0.1,迎角α=7◦,雷诺数Re分别取5.0×104,5.0×105,2.5×106和5.0×106,通过与采用当地时间步法的计算结果进行对比,分析检验算法在高雷诺数下的计算效率和稳定性.另外,将雷诺数为5.0×105时的计算结果与CFL3D[4]值进行对比,检验算法在高雷诺数下的可靠性.

表2给出了NACA0012翼型在不同雷诺数和CFL数时的计算状态和计算耗时情况,以及相同雷诺数下LBM与采用当地时间步法后计算状态的比较.本工作测得在CFL数为1.0时,满足计算稳定所需的最大雷诺数为5.0×104.因此,在此基础上进行比较分析.由式(9)可知,在松弛时间τ取定值时,如果υ值随着雷诺数Re变小,则时间步也应同比例的变小,因此在雷诺数增大时,通过控制CFL数改变时间步的大小,可使松弛时间τ保持不变.观察表2可知,随着雷诺数Re的增大,未采用当地时间步法的LBM计算状态发生了变化.当雷诺数逐渐增大,计算状态变得不稳定;当雷诺数继续增大时,数值计算趋于发散.图4是雷诺数为2.5×106时计算的残差收敛曲线,其中R为残差,T为迭代次数.由图可以看出:未采用当地时间步法的计算在最初阶段会出现震荡,最后经过一段时间后出现发散;而采用当地时间步法后,计算快速的趋于稳定.另外,采用当地时间步法后,高雷诺数下计算状态不稳定的现象得到了改善,CFL数作为局部时间步的调控参数,已不再受雷诺数的约束.在计算耗时方面,随着雷诺数的增大,计算耗时变化规律一致,但与未采用当地时间步法相比,采用当地时间步法可以缩短计算趋于稳定的时间,明显提高了计算效率.

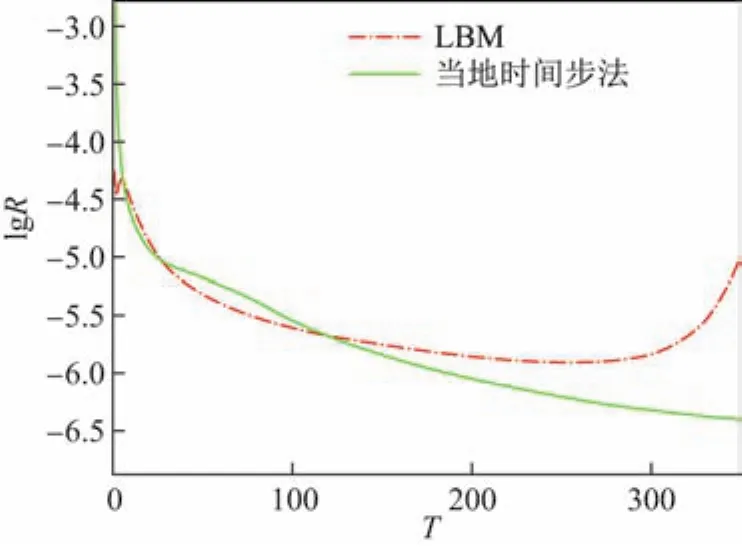
图4 计算残差收敛曲线(Re=2.5×106,α=7◦)Fig.4 Calculated error convergence curve(Re=2.5× 106,α =7◦)

图5 为翼型在雷诺数为5.0×104和5.0×105时表面的压力系数分布曲线.由图5(a)可以看出,两种计算结果有稍许不同,但基本吻合,表明是否采用当地时间步法对当前雷诺数下的结果影响不大.由图5(b)可以看出,二者的计算结果却发生了明显的变化.采用当地时间步法后计算的结果与CFL3D值吻合较好,而未采用该方法计算的结果偏差较大,特别是翼型尾缘处的压力系数分布.这是因为随着雷诺数增大,时间步变得更小,造成了计算的不稳定现象.

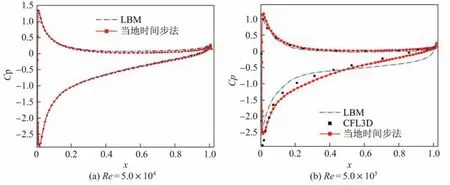
图5 NACA0012翼型表面压力系数分布曲线(α=7◦)Fig.5 Pressure coefficient distribution of NACA0012 airfoil surface(α =7◦)

未采用当地时间步法时,NACA0012翼型的流线如图6所示.由图可知,翼型上表面靠近尾缘处形成了明显的附着涡结构,这使得该位置的压力系数明显偏大.

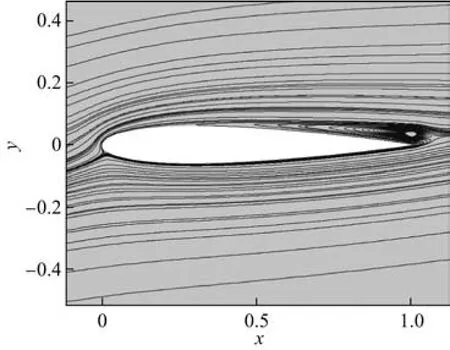
图 6 NACA0012翼型表面的流线图(Re=5.0×105,α=7◦)Fig.6 Airfoil flow chart of NACA0012 airfoil surface(Re=5.0×105,α =7◦)

图7 为雷诺数为2.5×106和5.0×106时翼型表面的压力系数曲线.由图7可知,曲线均没有出现大的变形,计算结果良好.

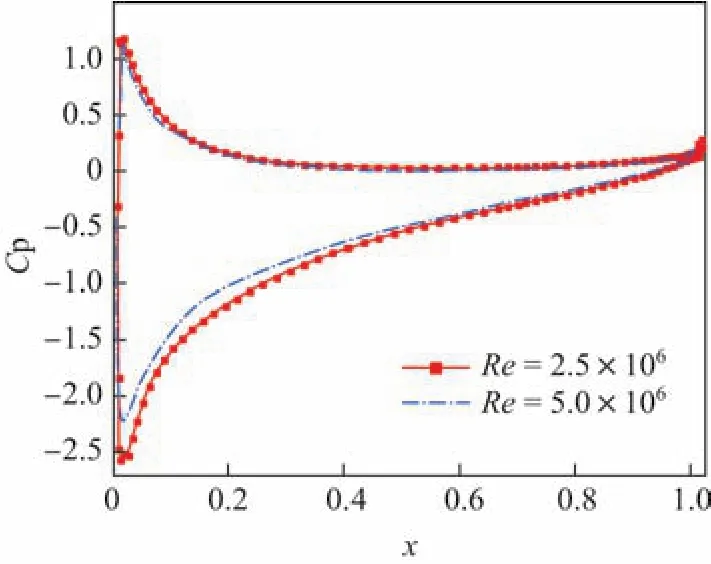
图7 NACA0012翼型表面压力系数分布曲线(α=7◦)Fig.7 Streamline diagram of NACA0012 airfoil(α =7◦)

6 结束语

高雷诺数流动下基于LBM方法的数值模拟,在理论和应用上都是十分重要的,同时它也是一项极具挑战性的研究课题.本工作在未使用湍流模型情况下研究了NACA0012低速绕流问题,并分别对算法可靠性、计算效率和稳定性进行了分析,通过与实验值进行比较,发现结果虽有所差异,但仍可接受.

研究结果表明,本工作结合分子运动论的相关原理,采用了在贴体网格GILBM框架下发展的当地时间步改进技术,对NACA0012翼型不同工况进行了数值模拟,该方法使得计算区域内的各点都可以采用满足CFL条件所允许的最大时间步长.因此,流场处处以稳定极限向前发展,这不仅改善了算法的计算稳定性,又提高了计算效率,从而增强了LBM方法在处理高雷诺数流动问题方面的适应性.本工作的算例计算结果与实验结果十分吻合,证明了该方法的准确性.