基于混合智能算法优化LSSVM的短期风压预测

涂伟平,李春祥

(上海大学土木工程系,上海200444)

对于跨度较大、高度较高、柔性强的建筑结构,风荷载是其建筑设计、施工及运营使用阶段的重要影响因素.建筑表面的风荷载,特别是非高斯性较强的脉动风,可能会使建筑物发生较大的风致振动,从而影响建筑的正常使用[1].因此,对风荷载特别是对非高斯性较强的脉动风荷载进行研究就显得很有必要.为获得建筑结构表面的风场数据,目前国内外主要有计算流体动力学(computational f l uid dynamics,CFD)、风洞试验、现场实测等手段.虽然现场实测方法操作困难、耗时耗资太大,获取风场数据受到很大限制,但确是研究风场特性最为真实和直接的手段,也能给目前的各种试验方法和理论模型提供坚实的指导[2].因此,利用现场实测方法获取风场数据是结构抗风研究的重点,也是研究风荷载的长期方向.

近几年,随着信息科学和技术的迅猛发展,越来越多的学者致力于使用数据驱动技术进行结构风场数据的预测.支持向量机(support vector machine,SVM)因计算速度快、预测精度高、控制参数少等优点而受到广泛应用.最小二乘支持向量机(least square support vector machine,LSSVM)大大简化了传统的支持向量机的计算过程,因此具有很大的实用性.利用已知风场数据对LSSVM训练建模预测未知风场数据方面的研究已经取得一定进展,其中对LSSVM的参数进行优化是近几年的一大热点.孙斌等[3]利用粒子群算法(particle swarm optimization,PSO)优化LSSVM后对原始风电场风速进行预测,大大提高了LSSVM的预测性能.曾杰等[4]使用蚁群算法(ant colony optimization,ACO)优化LSSVM后预测风电场风速,预测效果较为理想.对LSSVM进行参数寻优,大多数学者主要集中在单个的智能优化算法,将两个或者两个以上的智能算法进行结合来优化LSSVM参数的研究比较少见.本工作通过分析ACO和PSO的优缺点,将二者结合提出了基于混合蚁群和粒子群算法优化LSSVM的预测模型(ACO+PSO-LSSVM).ACO+PSO-LSSVM模型不仅结合了ACO强大的全局搜索能力和PSO运算速度快的优点,还解决了ACO迭代时间长和PSO容易陷入局部寻优的问题,进而改善了LSSVM的预测性能.为了验证ACO+PSO-LSSVM预测模型的实用性和优越性,本工作对某一建筑表面的风压进行单点和空间点预测,并与ACO-LSSVM和PSO-LSSVM模型的预测结果进行了对比分析.

1 LSSVM预测模型

1999年Suykens等[5]提出LSSVM的概念.LSSVM发展于SVM,是利用最小二乘线性系统代替SVM中解决凸优化问题用到的二次规划方法[6].LSSVM的基本原理如下:首先将原始空间Rn中的样本通过一个非线性映射φ(x)转换到特征空间ϕ(xi),并在特征空间ϕ(xi)中构造出线性决策函数

式中,φ(·)是非线性映射函数,ω是权向量,b是偏置量.基于结构风险最小化(structure risk minimization,SRM)准则,LSSVM的优化问题定义为

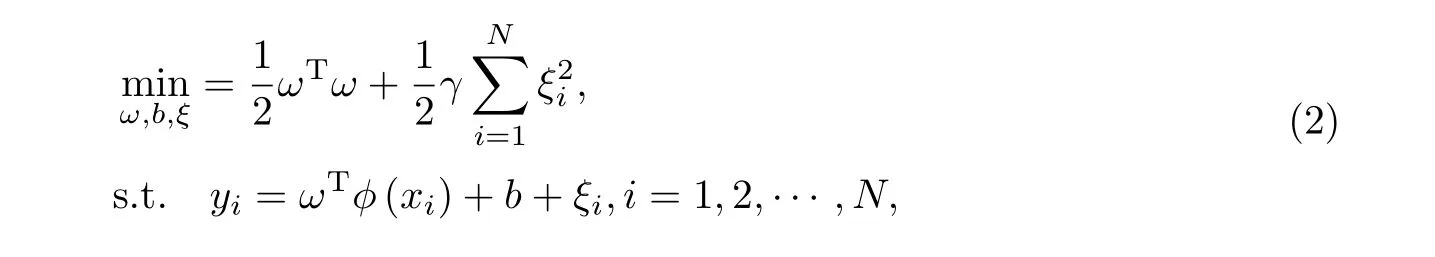
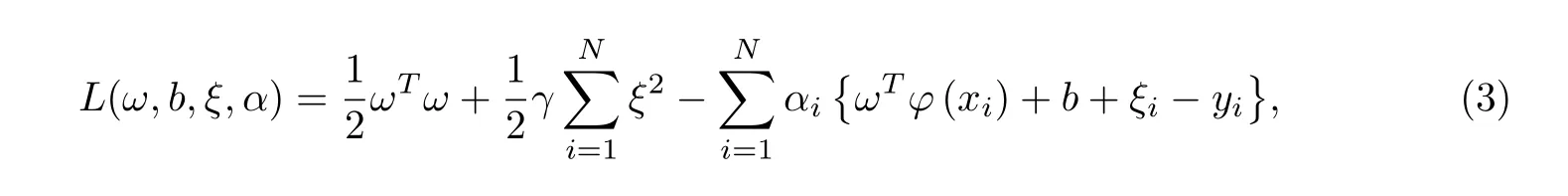
式中,αi为Lagrange乘子.根据KKT(Karush-Kuhn-Tucker)优化条件,依次对ω,b,ξ,α求偏导并令偏导数为0,可得到如下关于α和b的矩阵方程.

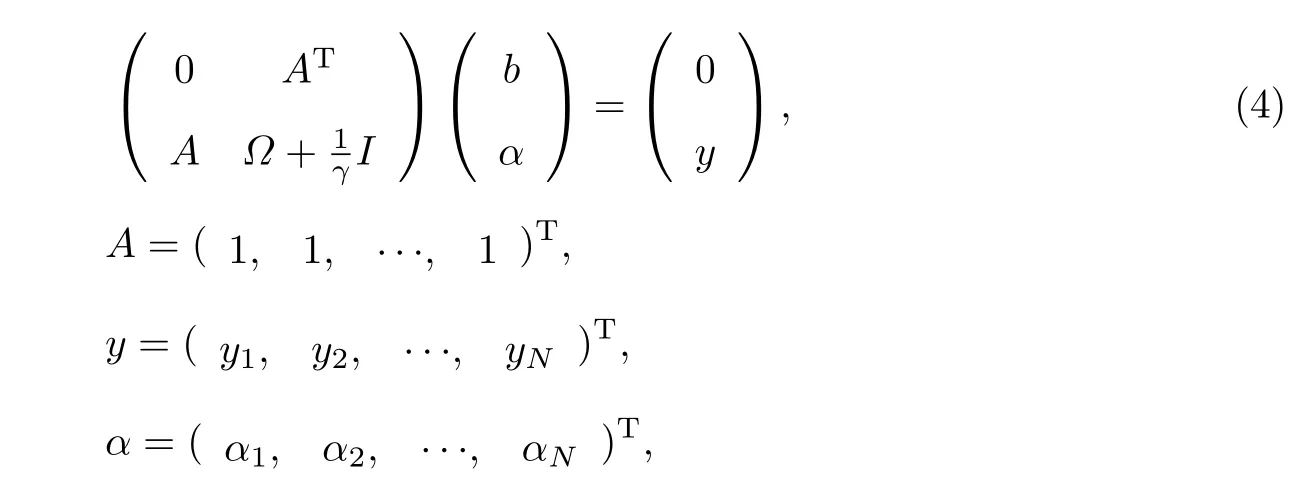
式中: Ω = φ(xi)T(xj)=K(xi,xj),i,j=1,2,···,N,K(·)为核函数;I 为单位矩阵. 经过求解,可得到LSSVM解决非线性问题的回归函数

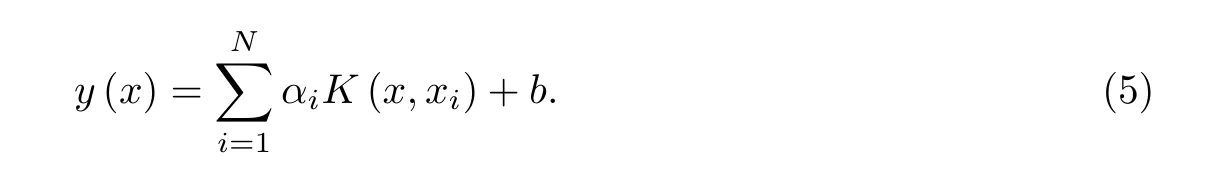
式(5)中核函数K(·)的类型直接影响LSSVM的性能,本工作选择应用最广泛的高斯径向基函数(radial basis function,RBF)作为LSSVM的核函数,即K(xi,xj)=exp(−kxi−xjk2/2σ2).在确定了核函数之后,LSSVM的控制参数只有核函数参数σ和正则化参数γ.

2 混合ACO和PSO

2.1 智能优化算法

蚁群算法[7]自20世纪由意大利学者Dorigo提出后,被不少学者应用于优化LSSVM的参数.该算法来源于对自然界蚂蚁群觅食行为的研究,通过人工仿照蚁群在觅食途径上留下的“信息素”的方法而找到所求问题的最优解。利用蚁群算法,对解空间参数化概率分布模型进行全局搜索产生最优解[8],并且不断更新产生的最优解,使得所求解始终保持在最优区域,增强了所求解的精确性.蚁群算法的缺点是求解过程较复杂、迭代时间长,并且在迭代过程中容易停滞;而优点是鲁棒性较强,精于全局搜索,且能很好地与其他优化算法进行结合.

粒子群算法[9]是一种新型的群体智能式算法.该算法通过人工模拟鸟群的觅食行为,在每一次迭代完之后对整个群体的最优位置进行更新,从而得到全局最优解.PSO的优点是结构简单,迭代时间短;缺点是迭代次数较多,很难跳出局部最优的陷阱,这也限制了PSO的广泛应用.

2.2 混合蚁群和粒子群的优化算法

通过上面的分析可知,ACO的优点可以弥补PSO的缺点,因此可将ACO和PSO进行结合形成基于混合蚁群和粒子群的优化算法(ACO+PSO)[10],该算法不仅结合了ACO强大的全局搜索能力和PSO运算速度快的优点,还解决了ACO迭代时间长和PSO容易陷入局部寻优的问题.混合蚁群和粒子群的优化算法主要分为两个阶段:①利用ACO在整个解空间内搜索寻优,找到最优解所在区域;②将ACO得到的寻优结果初始化PSO的粒子位置,再在局部解空间内进行搜索寻优,从而找到最优解的位置.

2.3ACO+PSO-LSSVM预测模型

利用混合蚁群和粒子群优化算法对LSSVM的核函数参数σ和正则化参数γ进行搜索寻优,算法的流程如图1所示.

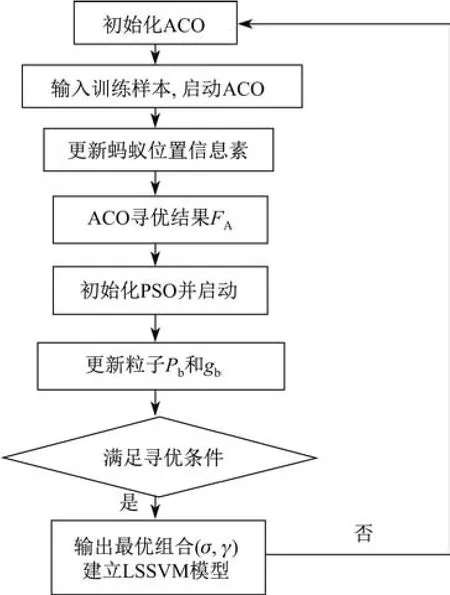
图1 基于混合智能算法优化LSSVM流程图Fig.1 Flowchart of hybridizing intelligent algorithm optimization based LSSVM

步骤1 将实测得到的风压数据样本划分为训练集和测试集,在训练模型之前对所有样本数据进行归一化处理:

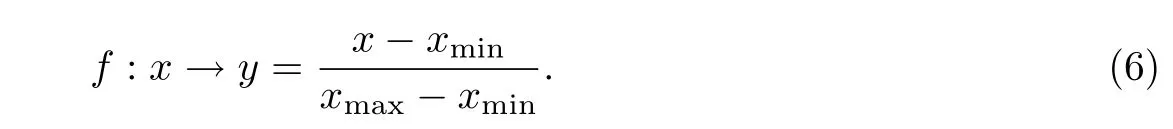
步骤2 初始化ACO的各种参数,在一定范围内随机产生核函数参数σ和正则化参数γ的组合(σ,γ)作为整个解空间集合I,并将蚂蚁随机放置在解空间I中.

步骤3 启动ACO,利用训练集对LSSVM进行训练学习.在训练过程中,第k只蚂蚁在t时刻从集合I中选择第j个参数组合(σ,γ)的概率为

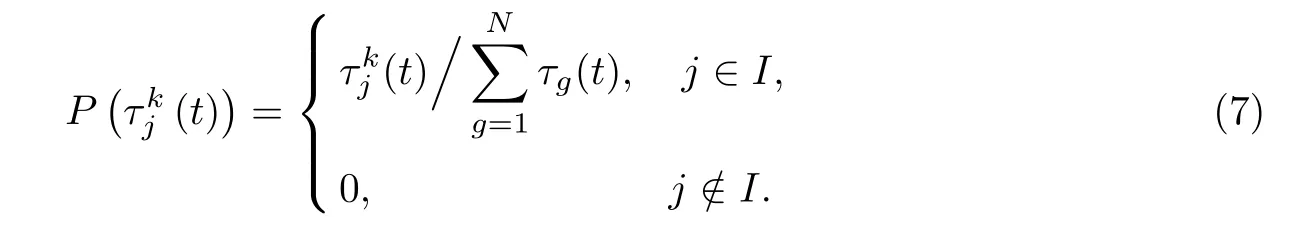
随着迭代次数的增加,需要更新解空间中j处的信息素浓度,即

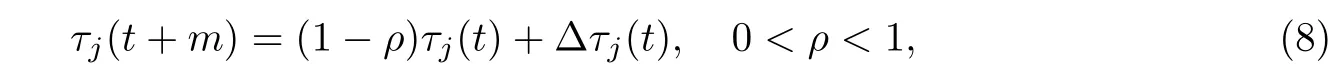
式中:ρ表示信息素的残留度;m为每次迭代所需时间;

yi和分别表示测试集的实际值和预测值,N表示样本数目.重复步骤3,得到的(σ,γ)置于集合FA内.

步骤4 初始化PSO的各种参数,把粒子群中各粒子随机放置在集合FA中,启动PSO,对LSSVM进行训练,通过计算各粒子的均方差,

找到个体最优值pb,经过迭代找到群体最优值gb.迭代过程中粒子的速度为

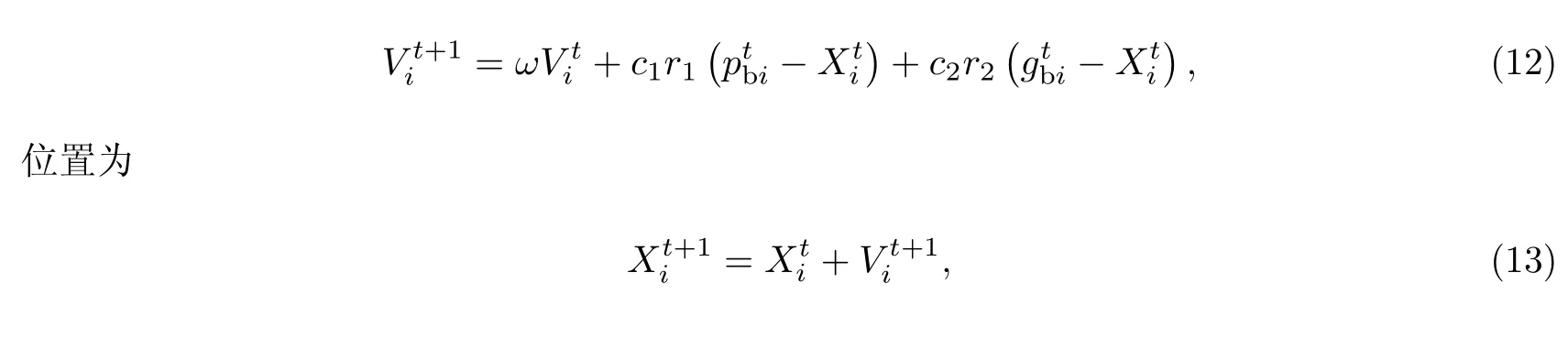
式中:c1,c2为加速度因子,变化区间为[0,2],一般取2;r1,r2在区间[0,1]随机取值.

步骤5 比较各粒子的个体最优值pb与群体最优值gb,如果pb>gb,则将gb更新为pb.重复上述步骤,将满足寻优条件的结果作为最优参数(σ,γ)输出;否则返回步骤3.

3 数值验证

对某工地一矩形建筑进行现场实测[11],实测点布置如图2所示.沿AB墙面竖直方向等间距布置5个测点,将实测得到风压时程样本作为原始数据.

图2 风压实测现场布置Fig.2 Layout offield measurement for wind pressures

3.1 单点风压

3.1.1 预测思路

由于LSSVM是将原始样本数据通过非线性映射函数映射到高维空间,实现数据的空间转换,因此需要对原始的数据样本进行相空间重构处理[4],确定LSSVM的输入和输出变量(Xt,Yt),其中Xt=(xt−1,xt−2,···,xt−m),Yt=xt,m为嵌入维数,xi为样本数据中的风压值.对LSSVM进行学习,训练出确定的输入输出关系,建立预测模型.

3.1.2 模型参数选取

令σ∈[10−1,102],γ∈[10−1,103],ACO和PSO的参数选取如表1所示.

表1 ACO和PSO的参数选取Table 1 Parameter selection of ACO and PSO

3.1.3 数值结果

为观察模型在不同高度的预测效果,取不同高度的2个测点(1#,3#)的300 s风压时程作为原始样本,如图3所示.将原始数据按照5∶1划分为训练集(前250 s,5 000个数据点)和测试集(后50 s,1 000个数据点),对模型进行训练并预测.

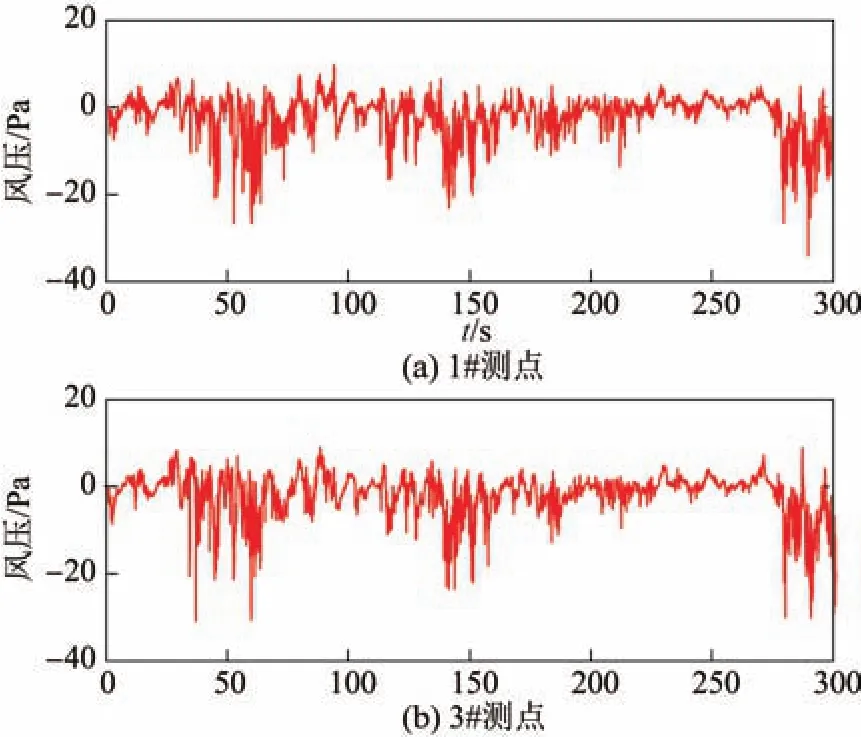
图3 1#和3#测点的原始风压时程图Fig.3 Time history of initial wind pressures on 1#and 3#

图4 是1#和3#两个测点的后50 s的预测风压与实测风压时程的比较.从图中可看出,3种算法对风压的预测值都比较接近实测值.在风压平稳和脉动性较小的阶段,3种模型的预测精度都很高,而在非高斯性强的风压点处,ACO+PSO-LSSVM的预测效果较ACO-LSSVM和PSO-LSSVM的预测效果要好.因此,ACO+PSO-LSSVM预测模型对脉动风压尤其是具有极值点的风压具有更好的预测效果.图5和图6分别是预测风压和实测风压的功率谱密度(power spectrol density,PSD)和自相关函数的对比.从图中可看出,两个函数曲线都吻合得比较好,进一步证明了ACO+PSO-LSSVM模型的预测效果良好.

根据平均绝对误差(mean absolute deviation,MAE)、均方根误差(root mean squared error,RMAE)及相关系数R评价3种预测模型的预测性能.表2给出了3种预测模型的评价指标对比.从表中可看出,对于同一测点,ACO+PSO-LSSVM的MAE和RMSE较ACO-LSSVM和PSO-LSSVM的要小,而R更大.另外,在实际计算过程中,ACO-LSSVM的耗时最长,ACO+PSO-LSSVM其次,PSO-LSSVM用时最短.图7为3种预测模型收敛速度的对比.由图7可以看出,ACO+PSO-LSSVM的收敛速度要优于ACO-LSSVM.因此,同时考虑计算时间和预测精度的情况下,ACO+PSO-LSSVM的预测性能最好.

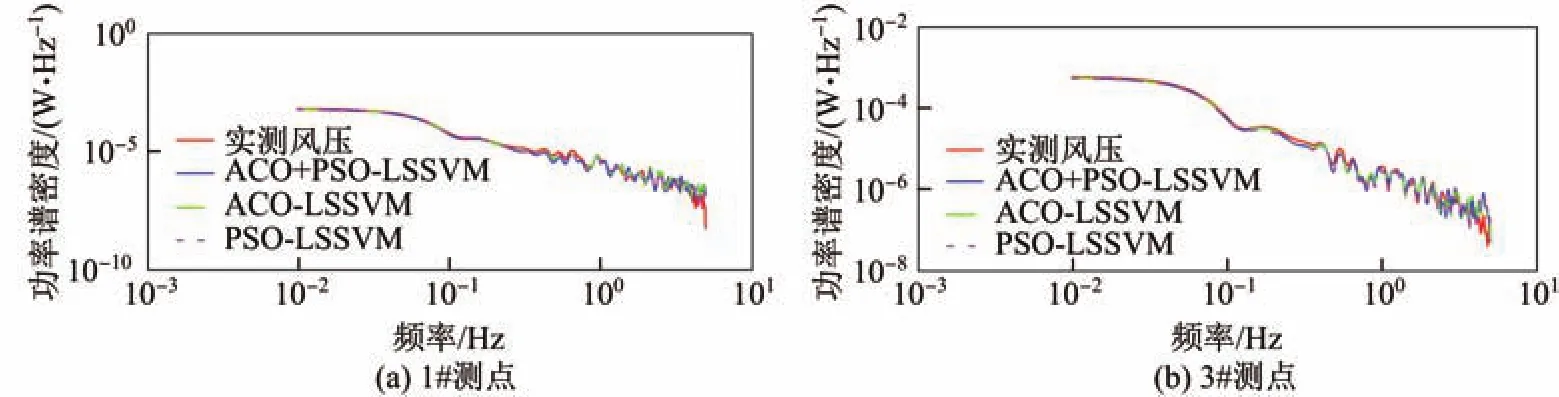
图5 3种模型预测风压实测风压的功率谱密度(1#,3#)Fig.5 Power spectrum tensity of predicted pressures with three algorithms and measured pressures(1#,3#)

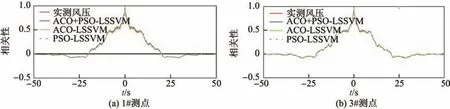
图6 预测风压和实测风压的自相关函数(1#,3#)Fig.6 Autocorrelation functions of predicted pressures and measured pressures(1#,3#)

3.2 空间点风压

取实测风压时程的前80 s作为建立模型的数据样本,其中前60 s(1 200个样本点)作为训练集进行内插学习,后20 s(400个样本点)作为测试集进行数值验证.为了验证预测算法在不同高度的有效性和稳定性,以1#和3#测点,2#和4#测点处的风压时程作为输入,2#和3#测点处的风压时程作为输出,采用3种预测模型进行数值验证分析.

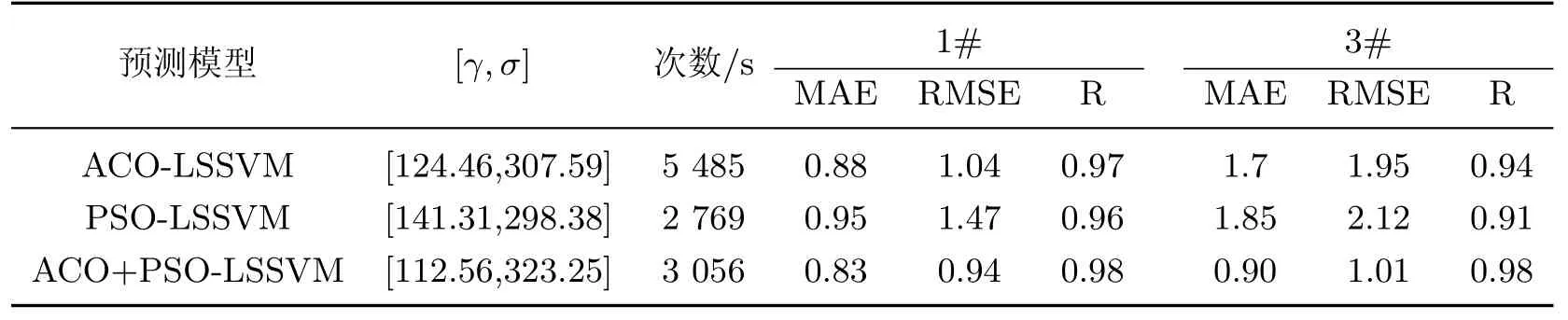
表2 3种预测模型的评价指标、LSSVM最优参数和耗时对比Table 2 Comparison of the parameters,LSSVM optimum parameters and time consuming for three prediction algorithms

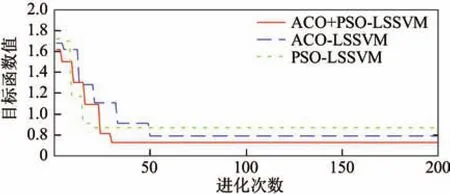
图7 3种预测模型的收敛速度(1#,3#)Fig.7 Rate of convergence for three prediction algorithms(1#,3#)

图8 是2#和3#测点后20 s的预测风压与实测风压时程图.从图中可以看出,3种模型的预测风压时程曲线基本贴近现场实测风压的时程曲线,对于呈现非高斯性的风压点处,ACO+PSO-LSSVM的预测效果较ACO-LSSVM和PSO-LSSVM要好.因此,ACO+PSOLSSVM预测模型对脉动风压,特别是具有极值点的不规则风压,具有更好的预测效果.图9和10分别是预测风压和实测风压的功率谱密度与自相关函数.从图中可看出,两个函数曲线都吻合得比较好,更好地证明了ACO+PSO-LSSVM效果.

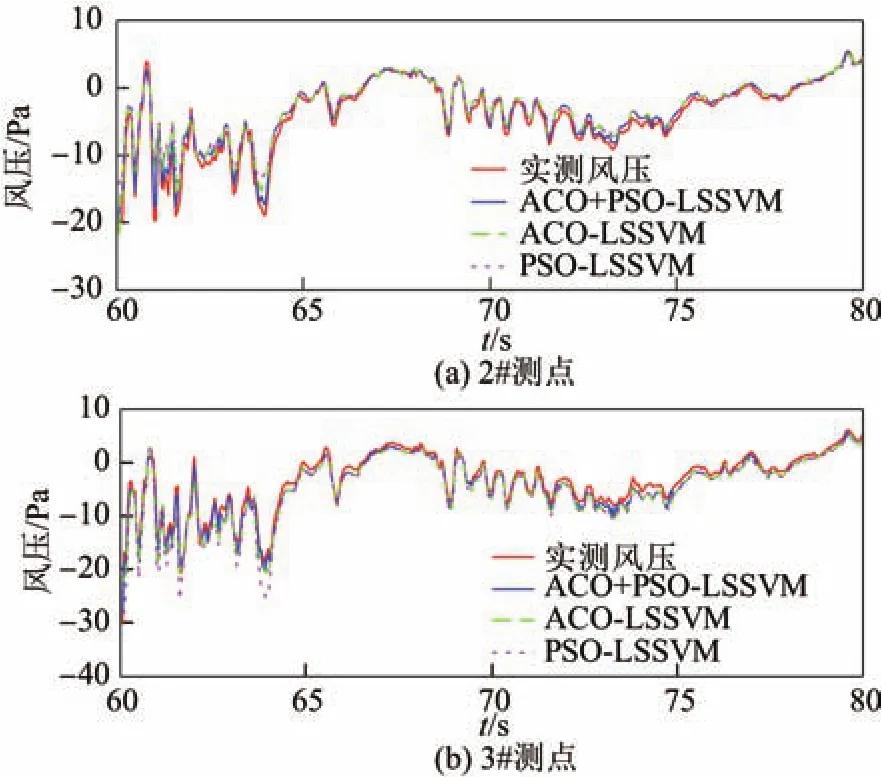
图8 预测风压和实测风压时程图(2#,3#)Fig.8 Time history diagram of predicted pressures and measured pressures(2#,3#)

图9 预测风压和实测风压的功率谱密度(2#,3#)Fig.9 Power spectrum density of predicted pressures and measured pressures(2#,3#)

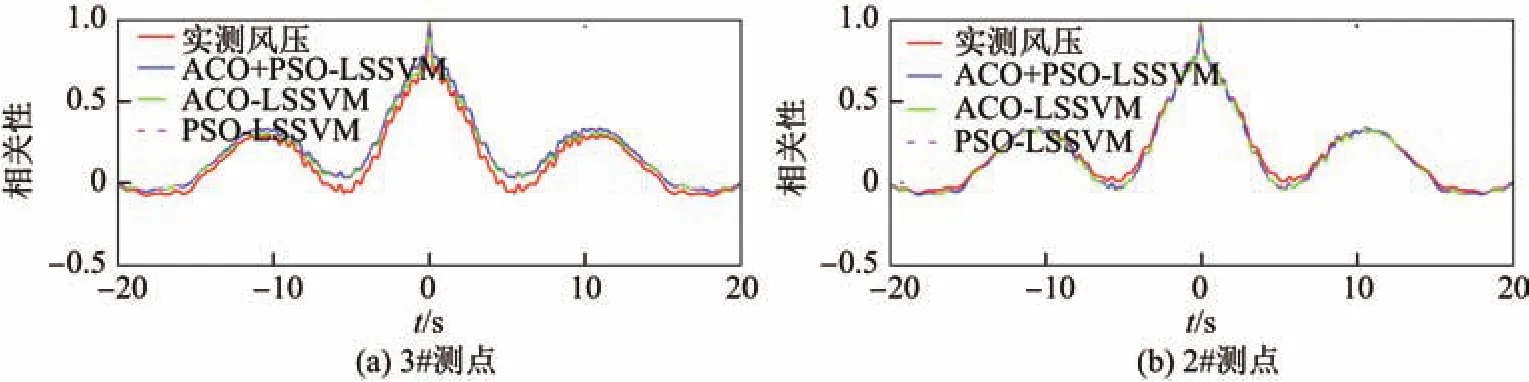
图10 预测风压和实测风压的自相关函数(2#,3#)Fig.10 Autocorrelation functions of predicted pressures and measured pressures(2#,3#)

根据平均绝对误差、均方根误差及相关系数3个指标评价预测模型的预测效果,结果如表3所示.从表中可以看出,对于同一测点,ACO+PSO-LSSVM预测模型的MAE和RMSE较ACO-LSSVM和PSO-LSSVM要小,而R更大.图11为3种预测模型收敛速度的对比.由图可以看出,ACO+PSO-LSSVM的收敛速度要优于ACO-LSSVM.

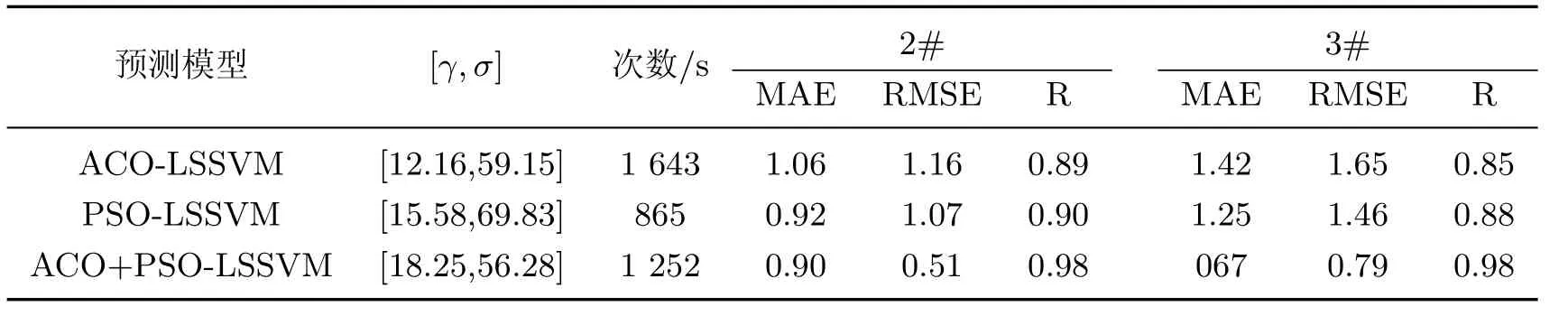
表3 3种算法的评价指标、LSSVM最优参数和耗时对比Table 3 Comparison of the parameters,LSSVM optimum parameters and time consuming by the three prediction algorithms

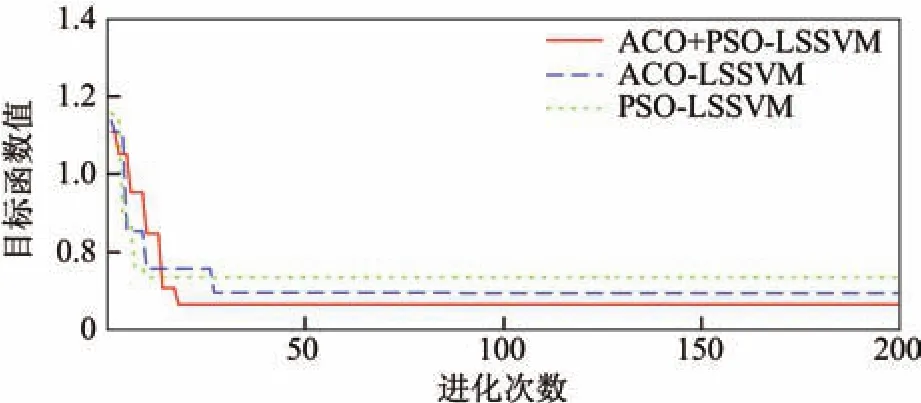
图11 3种预测模型的收敛速度(2#,3#)Fig.11 Rate of convergence for three prediction algorithms(2#,3#)

4 结束语

本工作提出了一种基于混合ACO和PSO优化LSSVM的方法,并对实测风压进行短期预测.ACO+PSO-LSSVM结合了ACO和PSO,避免了二者的缺点并实现优势互补集中,使用蚁群算法得到的初步寻优结果初始化粒子群中各粒子位置,从而减少了迭代时间,得到更优的参数输出.通过实测得到的风压数据对模型进行训练学习,建立了风压预测模型,对风压进行单点和空间点的短期预测均取得了较为理想的效果,验证了ACO+PSO-LSSVM对脉动风压的高预测性能.本工作为建筑表面风压的预测提供了理论指导,提出的模型具有较高的工程应用前景.

致谢 本工作中的数据来源于华东交通大学的李锦华博士,在此表示感谢!