两组分颗粒系统中凝并混合程度问题的多重蒙特卡罗模拟

姜 志,沈 杰,卢志明

(上海大学上海市应用数学和力学研究所,上海200072)

气溶胶系统广泛存在于自然界和工程领域[1-3],通常可以采用颗粒群平衡模拟(population balance modeling,PBM)的方法描述系统中离散相颗粒群的动力学演变过程.颗粒群平衡模拟是通过构建以颗粒尺度分布函数为基本量的颗粒群平衡方程(population balance equation,PBE)来描述颗粒“状态”,当研究对象是均匀流动或静止流体的系统时,称为零维空间系统,显然零维颗粒群平衡方程模拟是多维颗粒群平衡方程模拟的基础.

在气溶胶颗粒系统中,仅仅采用颗粒尺度这一个内部变量难以准确量化颗粒“状态”,颗粒表面积、组分、表面活化能、不规则度等颗粒群内部变量往往也随时间和空间不断演化,而这些颗粒状态参数在某些领域往往更受关注,如:燃烧生成的烟灰颗粒团聚体的不规则度和表面积与其毒性、吸附性等的关系[4-6];制药工业中不同组分药物的凝并混合[7-8]以及结晶过程[9].所以,考虑多组分或多变量动力学演变过程有广泛的工程和科学背景[2-3,10].Lushnikov[11]首先研究了两组分离散颗粒系统的凝并问题,并且给出了初始单分散条件下常数核模型的颗粒群平衡方程的解析解,得到在此初值条件下颗粒的组分分布为二项分布.随后,Gelbard等[12]给出了连续系统的多组分凝并问题PBE的解析解,以4种不同初始条件来阐明凝结和生长对颗粒演化组成分布的影响.Vigil等[13]研究了离散颗粒系统一个复杂加法核模型,得到其颗粒群平衡方程的渐近解,并指出颗粒的尺度分布函数是其中一个组分的颗粒尺度分布函数和高斯函数的乘积.近几年,Fern´andez-D´ıaz等[14-15]先后给出了两组分颗粒系统加法核和乘法核模型PBE的解析解,并对比了常数核、加法核、乘法核颗粒尺度分布函数解析解的表达式,得出它们和相应单组分情况具有相似的形式,以及这3种核对于小颗粒而言,只有乘法核的质量分布函数不随时间演化.Piskunov[16]给出了两个动力学事件(凝并和冷凝)同时作用的系统颗粒群平衡方程的解析解.Yu等[17]将文献[13]的问题推广到连续颗粒系统,并给出了与组分相关核模型(引入一个组分参数)的颗粒群平衡方程的解析解,分析了参数对颗粒尺度分布函数的影响.以上都是一些关于特殊核模型颗粒群平衡方程解析解的研究,由于PBE是典型的积分微分方程,对于多组分颗粒群而言,在高维空间进行积分微分十分困难,所以对方程的数值求解成为研究者关注的热点.Matsoukas等[18]和Lee等[19]运用常数目蒙特卡罗(constant-number Monte Carlo)法模拟了两组分颗粒系统的凝并过程,所考虑的核函数和组分无关,仅与总质量或总体积有关,并且还研究了系统组分之间混合程度参数(分散指数,segregation index,S.I.)的规律,得到分散指数将以一定形式减小.Zhao等[20-21]采用多重蒙特卡罗(multi-Monte Carlo,MMC)方法研究纳米颗粒布朗凝并问题,摒弃了Monte Carlo算法中广泛采用的“子系统”概念,引入了加权“虚拟颗粒”,模拟过程中保持虚拟颗粒数目和计算区域体积不变,从而在计算精度和效率上有很大改进[22-23].对于更复杂的核模型,Matsoukas等[24]提出了一个与组分相关的核模型,通过在核函数上引入组分“凝并效率”函数,使得核模型依赖于组分,但仅仅研究了一些简单核模型如常数核和加法核的情况,对于更实际且有物理意义的布朗核模型没有给出相应结论.气溶胶布朗凝并是气溶胶颗粒系统中由布朗运动导致颗粒间相对运动而发生相互碰撞黏结在一起的过程,该过程会改变气溶胶颗粒尺寸分布.而气溶胶系统的很多物理化学性质,如对光的散射性、毒性、扩散性等,都和颗粒尺寸分布有关.因此,对气溶胶布朗凝并理论的深入研究有重要的理论和现实意义.蒙特卡罗方法的一个重要特色是能够以一种简单而直接扩展的方式来处理高维问题,包括多变量系统.故本工作采用多重蒙特卡罗方法模拟了颗粒布朗凝并问题,主要关注颗粒凝并混合程度等问题,以及不同“凝并效率”参数及初值条件下,两组分颗粒系统中几个低阶矩统计量和描述不同组分混合程度的参数(即某个组分的总偏差和分散指数)的演变规律.

1 理论和方法

本工作的研究对象是一个颗粒总质量为M、颗粒总数目为N的两组分颗粒系统,为方便起见,把两个组分分别记为组分A和组分B.两变量PBE方程可由Smoluchowski方程推广而来[18,25]:

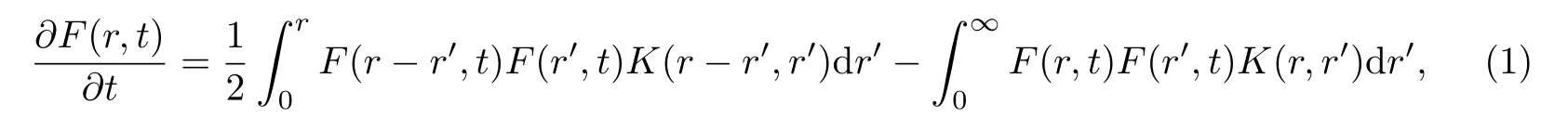
式中:r为颗粒群内部变量集,定义r=(v,m),其中m代表颗粒中组分A的质量(或体积),而v代表颗粒的总质量(或体积);F(r,t)表示颗粒群内部变量r的分布函数,所以F(r,t)dr表示t时刻、变量范围在r∼r+dr内的颗粒在单位体积内的数目浓度;K(r,r0)为核(kernel)函数,表示动力学事件发生服从的某种概率.故组分A在所有颗粒中的总质量分数(φ)可以定义为

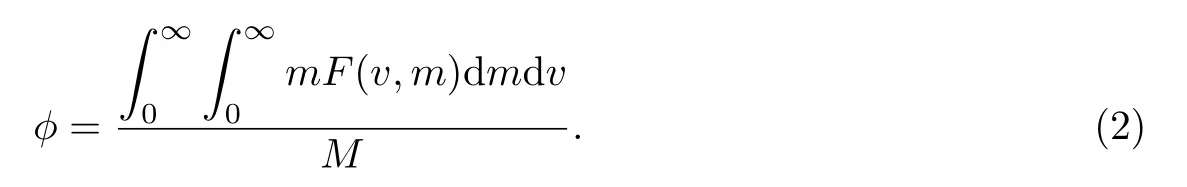
而组分A在某个颗粒中所占的质量分数为c=m/v.当颗粒系统达到一个完全混合均匀的状态时,两种不同质量分数虽然在表达形式上不同,但在数值上是相等的.但是,当系统还没有到达一个混合均匀的状态时,二者会有偏差.组分A的偏差定义为x=v(c−φ)=m−φv,则颗粒系统的组分A总偏差定义为[18]

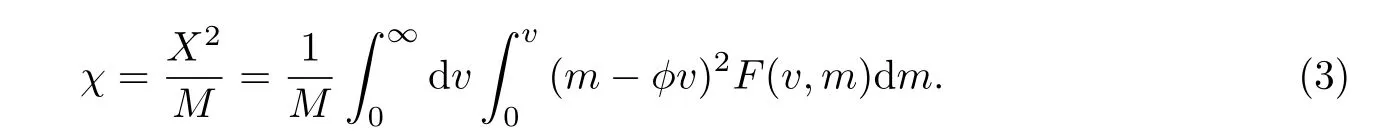
事实上,颗粒系统的组分A的总偏差χ和分散指数S.I.都是描述颗粒系统组分A的混合程度或均匀程度的参考指标.很多领域往往只需要研究颗粒群的几个重要平均量或整体量,即几个低阶矩来描述颗粒群的动力学演变.两组分颗粒的(k,l)阶的矩定义如下[26]:

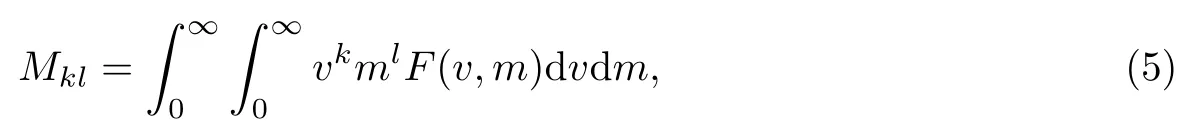
显然M00表示颗粒总数目浓度,M10表示颗粒的总质量浓度,M01表示组分A的总质量浓度,M11,M02,M20与颗粒系统的分散性有关.在引入矩Mkl后,很容易将组分A的总质量分数φ、分散指数S.I.改写为

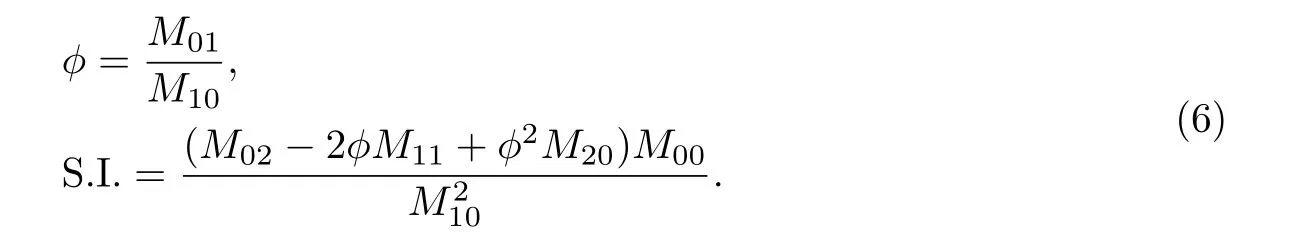
由于系统质量守恒,即M10,M01为常数,因此对两组分问题的凝并演化描述需要计算以下几个混合矩:M00,M11,M02,M20.

为了求解方程(1),本工作采用Zhao等[20-21]的多重蒙特卡罗方法,该方法发展了异数目权值虚拟颗粒策略,采用数目权值不等的虚拟颗粒群来代表实际物理颗粒群,尽可能多地继承了多分散颗粒群的尺度分布信息,具有高精度、高效率等优点[22-23].

2 结果与讨论

2.1 模拟工况

本工作研究的是颗粒凝并问题,考虑的核模型是由Matsoukas等[24]首次提出的,即

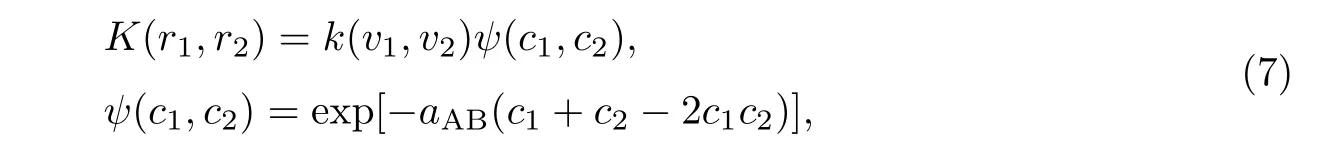
式中,ci表示颗粒i中组分A的质量分数,所以ψ(c1,c2)可以看成在一些常见核函数的基础上添加一个“凝并效率”函数.图1给出了“凝并效率”函数中的参数aAB对颗粒系统凝并的影响.由图1(a)可以发现,当aAB为正值(排斥)时,只含组分A或只含组分B的颗粒发生凝并的效率最高,而既含组分A又含组分B的颗粒发生凝并的效率最低,即颗粒组分不同不利于混合;在图1(b)中,当aAB为负值(吸引)时,结论恰恰相反,成分不同的颗粒凝并效率较低,有利于均匀混合.值得注意的是,当aAB=0时,核函数K(r1,r2)为原核函数k(v1,v2).Matsoukas等[24]研究了两个简单的核函数k(v1,v2)即常数核与加法核,但没有研究布朗核模型的情形.

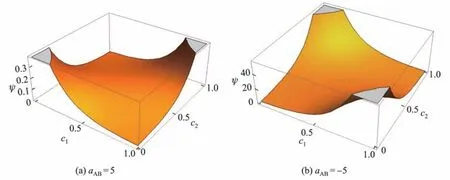
图1 效率函数随aAB的变化Fig.1 Collision efficiency as a function of aAB

布朗凝并核有两种形式,颗粒直接在纳米级的自由分子区布朗凝并核为(无量纲形式)

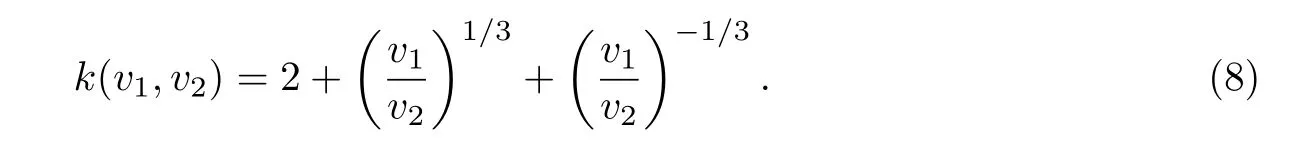
颗粒直径在微米级以上的连续区布朗凝并核为(无量纲形式)

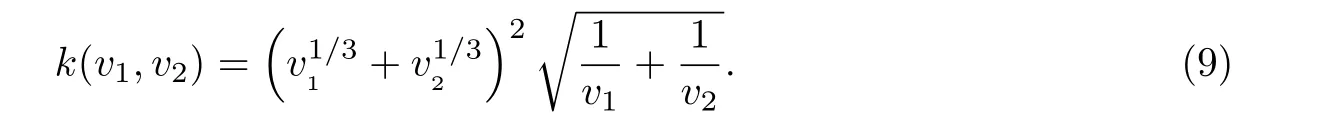
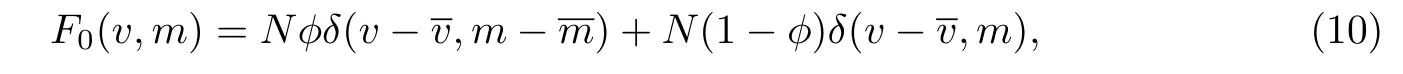
图2 不同两组分比例示意图(φ=0.5,0.4,0.3)Fig.2 Schematic of different proportions of two components(φ=0.5,0.4,0.3)

表1 初始分布(单分散)Table 1 Initial distribution(monodisperse)

2.2 低阶矩统计量的演化规律

在单组分系统中,气溶胶凝并过程存在自保持分布,各阶矩(3个)随时间的推移存在渐近行为[17,27-28],如随着时间以固定的标度律上升或下降. 在两组分颗粒系统中,研究的矩统计量有6个,其中两个矩统计量(M10,M01)保持不变,所以关注的矩统计量有M00,M11,M20,M02.图3给出了自由分子区和连续区初始分布φ=0.5系统中的无量纲颗粒总数浓度M00/M00ini随时间的演化,图中M00ini为初始M00,黑色表示只含组分A的颗粒.由图3(a)可以看出,对于自由分子区气溶胶布朗凝并过程,不论aAB取什么值,当凝并时间足够长时,无量纲颗粒总数目浓度与无量纲时间有如下关系:M00/M00ini∼τ−6/5;而由图3(b)可以看出,对于连续区气溶胶布朗凝并过程,不论aAB取什么值,当凝并时间足够长时,M00/M00ini∼τ.但是由图1可以发现,虽然aAB不会影响标度率的大小,但是会影响达到稳定标度率的时间,对于高排斥的“凝并效率”参数aAB=4或5时,需要更久的时间才能观察到随时间的标度率关系.同时,本工作也研究了其他几个无量纲矩统计量M11,M20,M02随无量纲时间的演化规律,发现其他几个无量纲矩也具有相同的渐近行为,但是在标度率上有所区别.对于自由分子区气溶胶布朗凝并过程来说,M11,M20,M02随时间的标度率为6/5;对于连续区气溶胶布朗凝并过程来说,M11,M20,M02随时间的标度率为1.需要指出的是,对于其他初始条件如φ=0.4和0.3下所得的结论和φ=0.5相同,在这里不一一指出.

2.3 组分A总偏差χ和分散指数S.I.的演化规律

下面研究两组分颗粒系统中,不同组分之间的凝并混合程度问题,其中组分A的总偏差χ和分散指数S.I.都是用来描述系统混合状态的参数,这里以初始φ=0.5为例,其他初始条件下结论类似.图4给出了自由分子区和连续区初始分布(φ=0.5)系统中组分A的总偏差χ随时间尺度的演化过程.可以发现,不论在自由分子区还是连续区布朗凝并过程,当aAB为负值时,χ迅速下降,然后随着时间的推移趋于一个稳定的值.这与预想情况相一致.由图1(a)可知:颗粒成分为组分A的(纯A)更容易与成分为组分B的(纯B)颗粒发生凝并,再加上给定的初始条件为纯A颗粒与纯B颗粒以1∶1混合,所以在初始阶段,混合较快.而当aAB为正值时,χ迅速上升,然后随着时间的推移也趋于一个稳定的值.这是由在初始状态下颗粒间的排斥作用导致的.值得注意的是,在排斥效应很强如aAB=4或5时,需要更久的演化才能发现χ趋于稳定值.图5给出了分散指数S.I.随时间尺度的演化过程,可以发现在不同aAB条件下,经过足够长时间的演化后,在自由分子区和连续区,分散指数S.I.和时间尺度存在如下关系:S.I.∼

图3 aAB不同时自由分子区和连续区气溶胶布朗凝并过程中无量纲颗粒数目M00/M00ini随无量纲时间τ的演变(φ=0.5)Fig.3 Evolution of normalized M00for Brownian kernel in the continuum regime and free molecular regime with different aAB(φ=0.5)

图4 aAB不同时自由分子区和连续区气溶胶布朗凝并过程中组分A总偏差χ随时间尺度的演变Fig.4 Evolution of power density of excess component A for Brownian kernel in the continuum regime and free molecular regime with di ff erent aABas a function of the time scale

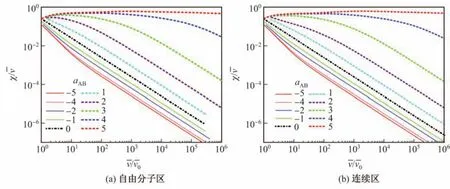
图5 aAB不同时自由分子区和连续区气溶胶布朗凝并过程中分散指数S.I.随时间尺度的演变(φ =0.5)Fig.5 Evolution of S.I.for Brownian kernel in the continuum regime and free molecular regime with di ff erent aABas a function of the time scale(φ=0.5)

由图4和5可以看出,系统最后都趋于一个稳定状态.为了进一步研究颗粒从初始阶段到稳定阶段的过程,以φ=0.5,aAB=4连续区的布朗凝并为例,将颗粒布朗凝并过程分为三个阶段(见图6):第一阶段(初始阶段),由于初始条件的影响S.I.随时间尺度迅速上升或下降;第二阶段(混合阶段)S.I.随时间尺度呈缓慢下降趋势,颗粒尺度变宽,排斥作用不占据主导地位,系统向混合均匀状态推进;第三阶段(稳定阶段)S.I.随时间尺度以下降,系统趋于自保持状态.

图6 连续区气溶胶布朗凝并过程中分散指数S.I.随时间尺度的演变(aAB=4,φ=0.5)Fig.6 Evolution of S.I.for Brownian kernel in the continuum regime as a function of the time scale(aAB=4,φ=0.5)

综合以上规律,可以得到χ经过长时间演化后会保持一个稳定的值,记为χ∞.事实上,将方程(3)两边同时对时间求导,再结合方程(1)可得[24]:

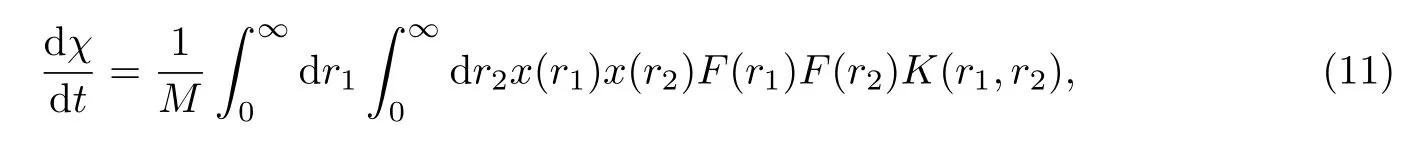
式中,x(ri)=(mi−),由Matsoukas等[18]得到的对于初始单组分的颗粒系统,无论方程的核函数是什么形式,方程(11)的右侧都将趋于零,即χ将趋于一个稳定值,这也验证了本模拟的可靠性.由方程(7)以及图1可知,随着aAB的增大,颗粒间的排斥作用越明显,凝并效率越低,并且结合方程(7)及χ∞的值,猜想χ∞随aAB存在指数函数关系.由于aAB的正负对系统凝并混合起完全相反的作用,故分别对这两种情况下χ∞与aAB进行拟合.图7和8分别给出了组分A总偏差的稳定值χ∞与“凝并效率”参数aAB的函数关系,图中FR为自由分子区,CR为连续区.由图可知,在不同的初值条件下,不论自由分子区还是连续区,χ∞与aAB可以用指数函数来确定,具体函数式如下:

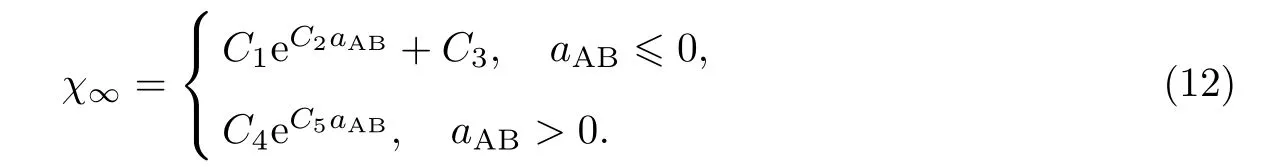
具体参数如表2所示(表中Ci为拟合参数),可以发现随着aAB的增大,χ趋于稳定的值将呈指数型增长.从增长趋势来看,不论在自由分子区还是连续区,当aAB为负值即组分相同时不利于混合,且随着aAB的继续增大,初始组分A的质量分数越大,χ∞值越大,颗粒系统质量分布越不均匀;当aAB为正值即组分相同时有利于混合,且随着aAB的继续增大,初始组分A的质量分数越大,χ∞值越小,颗粒系统质量分布越均匀.此外,由图4可知,当aAB=4或5时,需要消耗大量的计算机成本才能发现χ趋于稳定值,方程(12)可以预测在排斥效应比较强时组分A总偏差的稳定值,相应地可以预测颗粒系统的分布均匀程度.

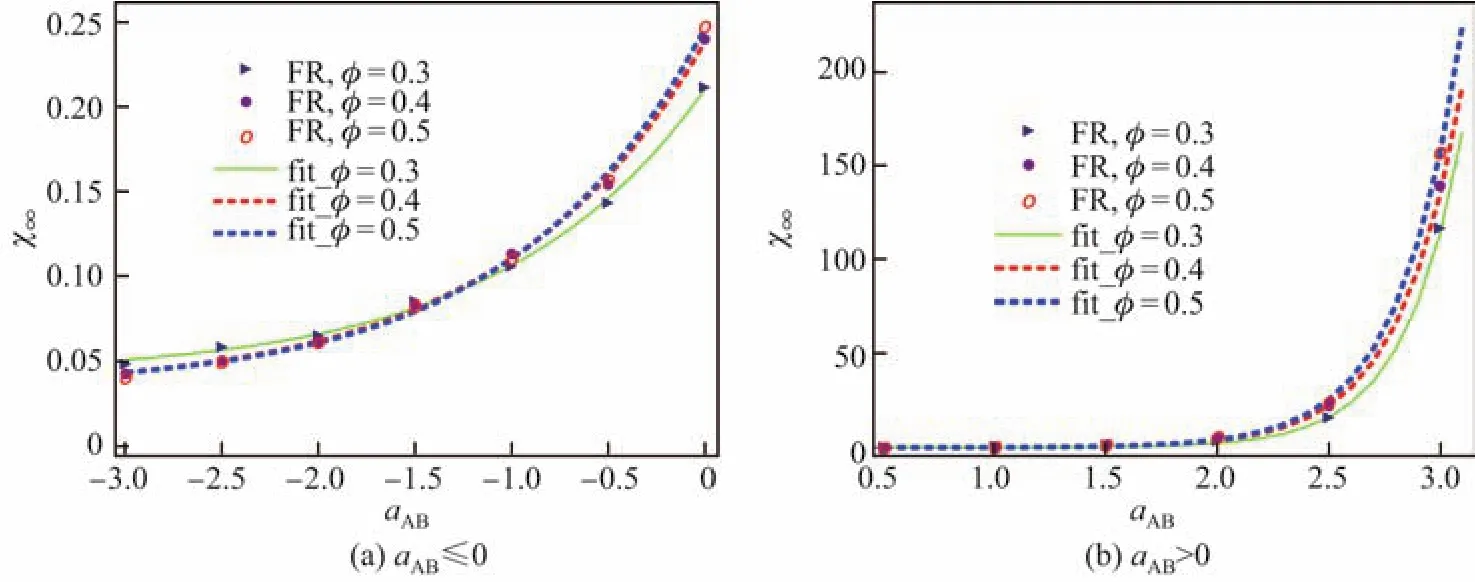
图7 不同初值条件下自由分子区气溶胶布朗凝并过程中组分A总偏差χ∞与aAB的关系Fig.7 Dependence of power density of excess component A,χ∞ on aABfor Brownian kernel in free molecular regime

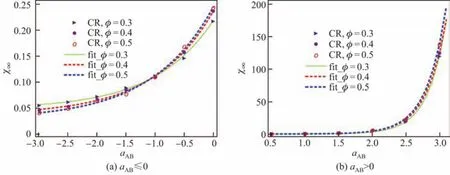
图8 不同初值条件下连续区气溶胶布朗凝并过程中组分A总偏差χ∞与aAB的关系Fig.8 Dependence of power density of excess component A,χ∞ on aABfor Brownian kernel in continuum regime

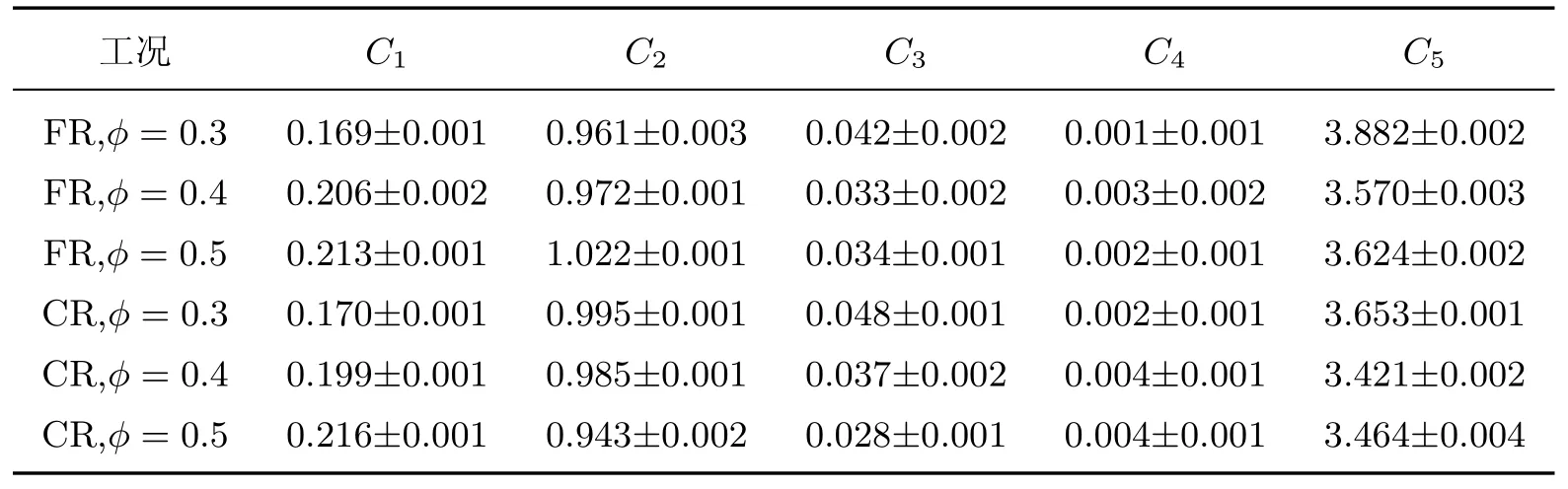
表2 不同初始单分散工况下的拟合参数Table 2 Coefficients of the fitted curves of different initial conditions

3 结束语

本工作利用多重蒙特卡罗方法模拟了两组分颗粒系统中与组分有关的核的布朗凝并问题.核模型中引入了“凝并效率”参数aAB,aAB值的正负会加快或者阻碍颗粒凝并过程.在某种机制或某几种机制作用下,颗粒群尺度谱将达到自保持分布[17,27-28],即颗粒尺度分布函数的所有特征变量在进行无量纲后具有稳定的表达式.本工作发现在自由分子区和连续区布朗核下,经充分长时间的演化后两组分颗粒系统的矩统计量也存在渐近行为,并且在自由分子区,M00∼ τ−6/5,M11,M20,M02∼ τ6/5;在连续区,M00∼ τ−1,M11,M20,M02∼ τ.当系统达到自保持状态时,系统混合度达到一个稳定值并且分散指数以下降,根据分散指数的发展过程可将系统演变分为三个阶段,即初始阶段、混合阶段、稳定阶段.在初始阶段,由于凝并效率参数的影响,S.I.随时间尺度迅速上升或下降;随着时间的推移,S.I.随时间尺度呈缓慢下降趋势,颗粒尺度变宽,排斥作用不占据主导地位,系统向混合均匀状态推进;经长时间演化后,S.I.随时间尺度以下降,系统趋于自保持状态.反之,当S.I.随时间尺度以1/v下降时,认为此时系统达到稳定阶段或者处于自保持状态.为了研究当系统达到自保持状态下组分A的不均匀性,通过拟合得到不同初值条件下组分A的总偏差的稳定值与“凝并效率”参数aAB的函数关系,发现二者之间为指数函数关系,此关系式可以用来预测排斥作用比较强的情况下组分A总偏差的稳定值.