基于改进蚁群算法的血管介入手术路径规划

2019-05-13高明柯陈一民张典华李泽宇

上海大学学报（自然科学版） 2019年2期

高明柯, 陈一民, 张典华, 黄晨, 李泽宇,3

(1.上海大学计算机工程与科学学院,上海200444;2.上海大学数码艺术学院,上海201800;3.上海交通大学医学院附属瑞金医院计算机中心,上海200025;4.中国电子科技集团公司第三十二研究所,上海201808)

血管介入手术是指医生在病人皮肤上做极小切口,用微细导管等器械通过人体血管对病灶局部进行治疗的方法,具有出血少、创伤小、恢复快的优点.目前,由于全国各地医院硬件配置和人员手术水平不一,大部分的血管介入手术仍然依靠有经验的外科医生,通过徒手操作导管并借助X射线等医学成像技术和虚拟现实等计算机辅助技术来完成.这类手术难度大,精度要求高,培训周期长,并且手术过程中病人和医生会受到X射线的辐射.在有限的技术条件下,综合考虑医生的操作水平、手术的危险性、术后并发症等因素,医生通常选用较粗的主动脉作为手术路径,而不考虑其他可能的最优路径.在密集分布的血管拓扑结构中,综合考虑手术器械的粗细,血管的长度、口径和迂曲程度等因素,必然存在一条从手术入口到病患之处的最优手术路径.因此,为了缩短手术时间,减少术后并发症,降低手术风险,提高手术成功率,在血管三维几何空间中寻找一条全局最优或次优的手术路径,对血管介入手术具有重要的理论指导和实际操作意义.

国内外对血管内路径规划的研究主要集中在虚拟内窥镜[1]和血管内导航技术[2],其关键技术是血管中心线的提取和导航路径的规划.提取中心线的方法有拓扑细化法[3]、距离变换法[4]、势能场法[5]、基于水平集法[6]和基于分割的方法[7-8]等.外科医生利用虚拟内窥镜技术,使用虚拟相机沿着血管中心线最大范围地窥视血管内的情况,用以进行术前的路径规划,确定手术路径.Wink等[9]采用Dijikstra算法和A星算法从预定义的代价图像中确定最小代价路径,并从医学图像数据中提取血管中心线.Belharet等[10]采用快速行进法在提取的血管中心线上搜索到两点之间的最短路径.但是,这些方法在搜索过程中并没有考虑血管的其他特性.

蚁群算法是仿生学中的一种群体智能算法,是1996年Dorigo等[11]受到蚂蚁觅食行为的启发后提出的.蚁群算法在医疗方面被应用于视网膜视盘识别[12]、乳癌诊断[13]、手术安排分配[14]等.目前,国内外基于蚁群算法的三维路径规划主要集中在无人机[15-16]、潜水器[17]、三维管道[18-19]和机器人[20-21]等方面,而与血管介入手术相关的研究暂未见文献报道.

针对上述问题,本工作提出在血管中心线提取的基础上,综合考虑导管直径,血管长度、最小直径、最大曲率和最大挠率等因素,引入端结点因子,改进蚁群算法中的启发式函数和信息素更新机制,辅助外科医生规划手术的最优路径.

1算法

1.1 蚁群算法

在蚂蚁的觅食过程中,每一只蚂蚁都会在走过的路径上释放一种可以与其他蚂蚁进行信息交流的化学物质,称之为信息素.随着时间的推移,信息素会挥发,因此蚂蚁爬行的路径越短,留在路径上的信息素浓度相对越高.蚂蚁能够发现这种信息素并感知它的浓度,并以较高的概率选中信息素浓度最高的路径.因此,含有高浓度信息素的路径会将更多的蚂蚁吸引到这条路径上,形成一种正反馈.基于上述原理,蚂蚁便能快速地找到一条离食物源最短的路径.

1.2 启发式信息

启发式函数对算法的收敛性和稳定性具有重要的影响.在蚁群算法中,启发式信息η通常定义为两点之间距离的倒数,即1/LI,J.基于手术的安全性和血管的特性,本工作中的路径规划不仅要考虑血管的长度L、血管路径段上的最小直径Dmin(大于导管直径Dc,确保导管能够穿过血管),还需要考虑血管的最大曲率Cmax和最大挠率Tmax,即血管弯曲程度和扭曲程度,启发式地选择较短且具有较好通过性的血管路径.因此,本工作中启发式信息定义为

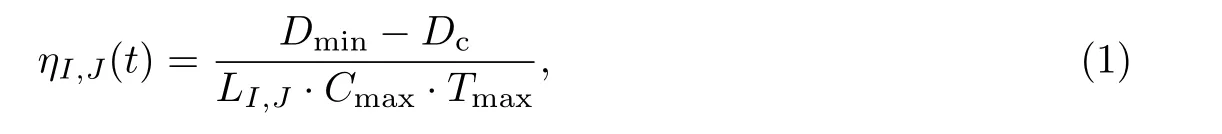
式中:ηI,J(t)表示I(x,y,z)到J(i,j,k)的启发信息;Dmin表示这条路径上血管的最小直径,Dc表示导管直径,需满足Dmin>Dc;LI,J表示当前路径长度;Cmax表示当前路径的最大曲率;Tmax表示当前路径的最大挠率.

1.3 概率机制

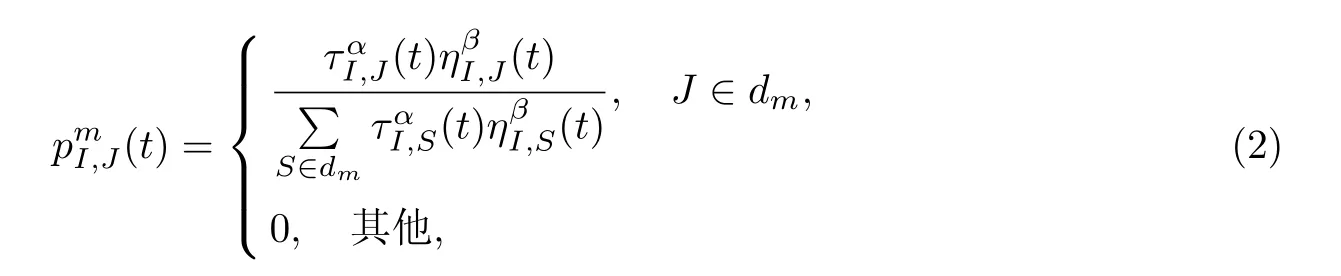
1.4 信息素更新机制

初始时刻各路径上的信息素量是相等的.蚂蚁在完成一次循环后,会在相应路径上留下信息素,但是信息素会随着时间的推移逐渐挥发,因此要对信息素浓度进行更新.由于只针对病人手术范围和具体手术部位进行计算机体层成像(computed tomography,CT)血管造影,因此得到的血管网络拓扑结构不是一个完全图,有的结点之间不存在回路,必然存在一些异常结点,即端结点VG(度数为1).若蚂蚁在搜寻过程中访问到一个端结点VG且该结点并非终点VE时,则结束搜索,定义搜索无效并删除该结点.由于蚂蚁在本次循环中不更新信息素,因此引入端结点因子γm以改进信息素更新机制.

基于上述分析,在蚂蚁进入下一个循环之前,相应路径上的信息素做如下更新:

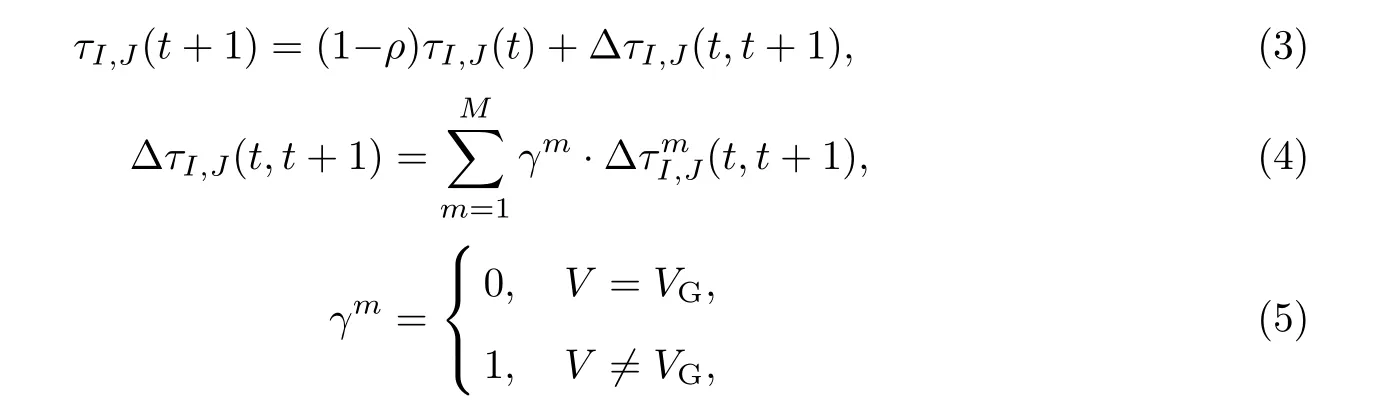
式中:ρ(0<ρ<1)为信息素挥发系数,1−ρ为信息素残留因子;(t,t+1)表示第m只蚂蚁在第t次循环中在路径(I,J)上留下的信息素量,(t,t+1)表示本次循环当中所有经过路径(I,J)的蚂蚁留下的信息素增量;γm为端结点因子,表示本次循环中蚂蚁m在搜索过程中是否遇到端结点.考虑到全局最优的路径情况,从手术安全和路径最短的目的出发,本工作在蚂蚁完成一次循环后再更新信息素.

1.5 信息素更新模型

信息素更新模型是蚁群算法的随机搜索与快速收敛的重要环节.根据信息素更新模型的不同,Dorigo等[11]提出了3种蚁群系统:蚁密系统、蚁量系统和蚁周系统.由于蚁密模型不考虑路径因素,且蚁量模型只在局部更新信息素,因此根据问题的实际情况,为了防止陷入局部最优,采用蚁周模型,即在蚂蚁循环一次后更新信息素.考虑到血管直径和导管直径在手术中的影响,蚁周模型修改为

式中:Q为信息素强度常量,表示蚂蚁在一个循环中在所经过的路径上释放的信息素的总量,在一定程度上影响算法的收敛速度;Lm表示第m只蚂蚁在此次循环中所经过的路径长度.

1.6 算法描述

血管介入手术路径规划算法的流程如图1所示.

2实验

实验平台:CPU为Intel(R)Core(TM)i5-520M,频率2.4 GHz,内存6 GB;操作系统Windows 7旗舰版;软件采用Visual Studio 2010,VTK,ITK,VMTK,Matlab 2012a.

2.1 血管建模及中心线提取

血管的三维建模方法主要有体绘制和面绘制两种,而根据建模过程中是否存在模型假设,又可粗略分为基于模型和无模型两类方法[22].由于基于模型的方法通常假设血管的剖面轮廓为圆形,而这种假设不能真实地表示任意剖面,例如,病变血管的剖面可能不是圆形.无模型的方法更忠实于初始数据,可以适用于疾病诊断等精度要求较高的场合.因此,本工作采用无模型的方法,并根据Antiga等[23]提出的通过基于水平集的方法进行分割建立血管三维模型,再用基于Voronoi图和Eikonal方程的方法提取血管中心线,并求得最大内切球半径.根据合作医院放射科提供的腿部CTA数据进行建模并提取血管中心线,结果如图2所示.

2.2 路径规划实验

为了评估信息素启发因子α,期望值启发因子β,蚂蚁数量M,信息素总量Q和信息素挥发系数ρ(0<ρ<1)对算法的影响,本工作设置7组不同的参数组合,每组做10次实验,最后取平均,结果如表1所示.由表1可以看出:参数组合4所需的计算时间t最短,主要原因是ρ较大,即1−ρ较小,此时路径上残留的信息素较少,导致正反馈作用占主导地位,搜索随机性减弱,因此收敛加快,陷入局部最优;参数组合5所需的计算时间最长,主要原因是蚂蚁的数量增大,虽然加强了搜索随机性,但是收敛减慢.通过比较,本工作最终选定α=5,β=10,M=40,Q=100,ρ=0.5,此时整个算法的平均计算时间为9.53 s.实验设置迭代100次,起点为128,终点为53,导管直径为0.2 mm.腿部血管网络拓扑结构(76条路径,131个端点)和最终得到的路径规划结果如图3所示.

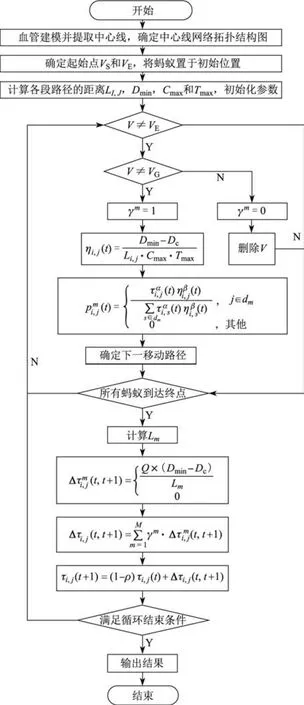
图1 血管介入手术路径规划算法流程图Fig.1 Flow chart of path planning algorithm for vascular access surgery

2.3 算法比较实验

为了横向比较算法的效率和可靠性,选取路径规划仿真实验中的参数取值,导管直径分别取值为0.5和0.2 mm.分别采用Dijkstra算法和本算法进行路径规划,结果如表2所示.

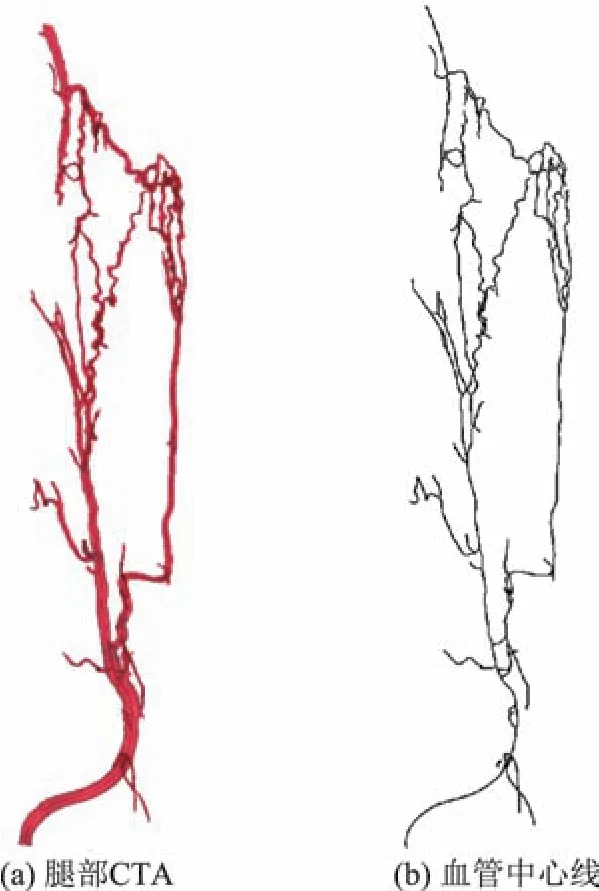
图2 腿部血管中心线的提取效果示意图Fig.2 Schematic diagram of vascular centerline extraction in legs

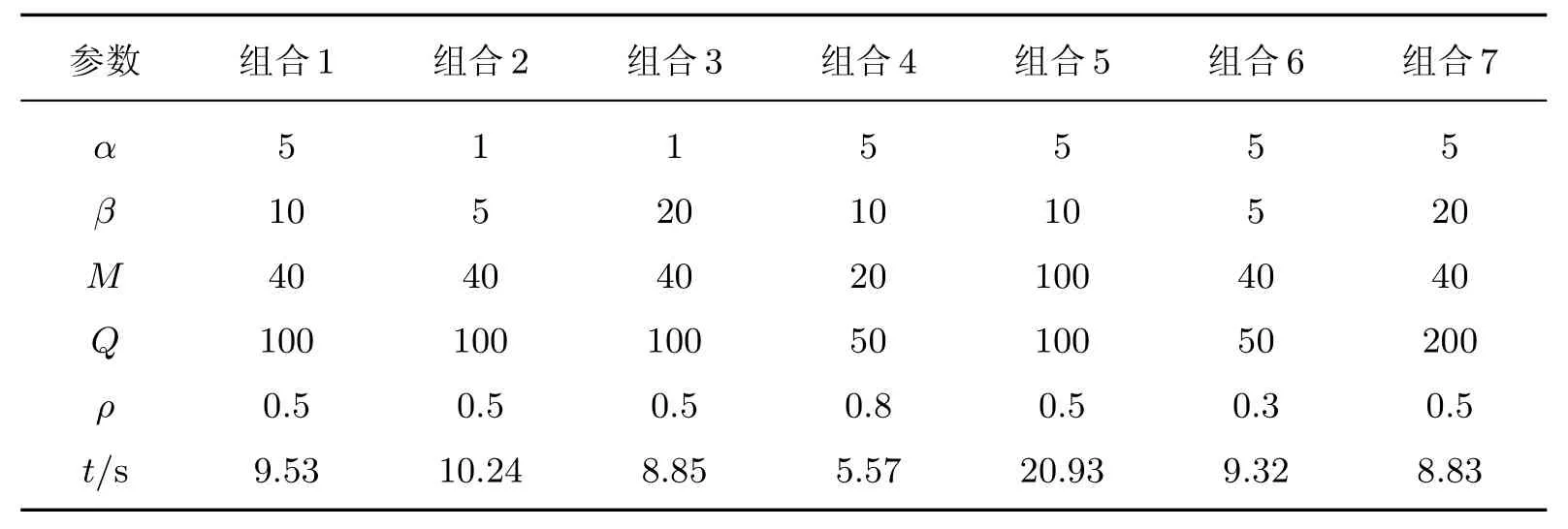
表1 血管介入手术路径规划的参数设置Table 1 Parameter setting of path planning for vascular access surgery

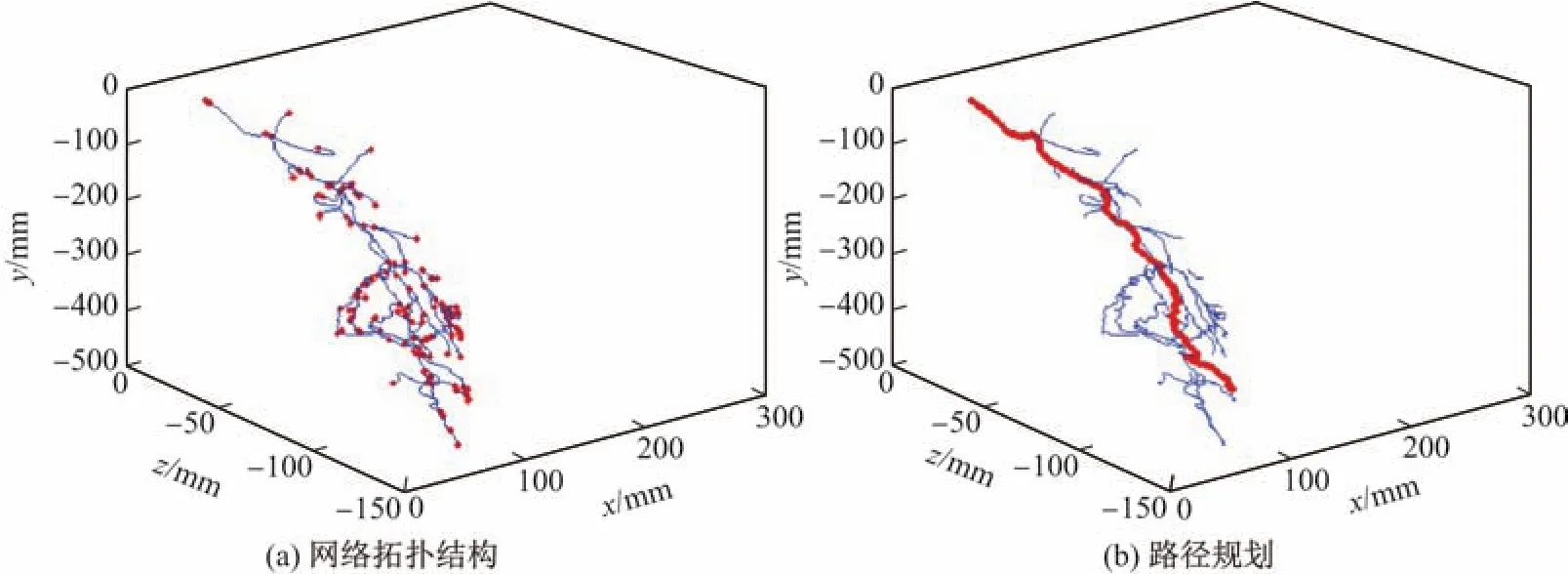
图3 腿部血管的网络拓扑结构和路径规划Fig.3 Network topology and path planning of vascular in legs

表2 两种不同路径规划算法的比较Table 2 Comparison of two different path planning algorithms

由表2可以看出:从起点128到终点53,由于Dijkstra算法不考虑导管直径以及血管的直径、曲率和挠率,因此执行速度快;本算法在导管直径为0.2 mm时,路径规划结果与Dijkstra算法一致,但执行时间较长;导管直径为0.5 mm时,本算法得不到正确的路径规划结果,终止在点50位置.由于导管无法通过点50到点51,因此该路段的最小直径为0.248 4 mm.实验结果表明,Dijkstra算法虽然执行速度较快,但是实际规划的路径结果并不可靠,由于在导管直径为0.5 mm时,点128到53之间不存在最优路径,因此表明本算法比Dijkstra算法安全可靠.