LTE-M用于轨道交通CBTC的时延分析

张 睿,郑国莘,解钧捷

(上海大学特种光纤与光接入网省部共建重点实验室,上海200444)

2015年中国城市轨道交通协会根据工信部原[2015]65号文件的要求,规定1 785∼1 805 MHz频段的时分长期演进系统(time division long term evolution,TD-LTE)用于城市轨道交通基于通信的列车控制(communication based train control,CBTC)系统,并发布地铁长期演进系统(long term evolution-metro,LTE-M)技术规范,规定通信系统单路单向传输时延不超过150 ms的概率不小于98%,不超过2 s的概率不小于99.92%,以满足CBTC对数据通信可靠性的需求.一般列车位置信息以600 ms为周期发送至区域控制器,同时,列车行驶许可信息以600 ms为周期从区域控制器发送至车载设备,且这两种信号时延超过150 ms时即视为失效.当连续1.8 s内轨旁区域控制器没有收到列车的有效位置报告信息或有效行驶许可信息时,列车会发生紧急制动,进而影响轨道交通全线安全运行.因此,研究LTE-M用于CBTC的时延十分必要.步兵等[1]分析了传输时延对列车控制系统性能的影响.Nguyen等[2]研究了信号时延、切换特性、连接丢失与重传机制对数据包传输失败率的影响.Khayat等[3]提出了LTE用于城市轨道交通中的CBTC系统以及CCTV系统的服务质量(quality of service,QoS)分析.Sniady等[4]对LTE用于欧洲列车控制系统(Europe train control system,ETCS)的情况进行了特性分析.潘美莺等[5]对电话网中一个具有转发功能节点上的业务情况进行了排队论建模.张柏生等[6]使用排队论中的M/M/1模型对网络通信进行建模,并求得缓冲区长度等值的计算方法.陈雅等[7]使用排队论模型分析了航天测控网络通信信号的实时性.徐雪飞等[8]基于排队论分析了军事航空通信系统的频率干扰问题,并给出了模型的运算流程和基本方法.但是,关于LTE有限的带宽能否满足CBTC数据通信低时延需求尚未见文献报道.

本工作采用排队论的基本理论,分析了不同场景下多车数据流量随机性接入时的性能.首先,通过对CBTC系统的通信模型和LTE系统的信号模型进行了建模,使用排队论的基本理论对信号的等待时延进行了理论计算;然后,在不同带宽、不同业务流量的情况下对LTE用于CBTC数据通信系统的信号时延进行仿真分析,并与理论值进行对比,得出其对CBTC通信系统的影响.

1 LTE-M系统模型

1.1 通信模型

LTE-M用于CBTC通信系统时,为了可靠传输,车头车尾各有一个无线单元分别接入两个独立的LTE网络.为分析简单,本工作分析单网运行的情况.一般每个车站放置一个基站构成一个小区,而当一个车站基站发生故障时,单小区极限情况下至多应容纳6辆列车.如图1所示,每辆列车各布设一部车载控制器(carborne controller,CC),每台CC与一台终端接入单元(terminal access unit,TAU)连接,通过车载天线与轨旁设备进行通信信号传输.

图1 LTE-M用于CBTC数据通信系统模型Fig.1 Data communication system model of LTE-M in CBTC

轨旁设有区域控制器(zone controller,ZC)、线路中心单元(line connector,LC)、连锁控制器(computer interlocking,CI)、列车自动监控系统(automatic train supervision,ATS)、维护监测子系统(maintenance support system,MSS)、时间服务器等6种设备接入核心网(evolved packet core,EPC),通过基带处理单元(base band unite,BBU)连接射频拉远模块(radio remote unit,RRU)与车载设备实现通信.

由于位于小区边缘的列车通信情况最为恶劣,因此本工作分析该情况下CBTC数据流接入过程中的时延.

1.2 排队模型

LTE-M接入方式为车载终端将多种不相关的车辆信息随机向基站传输,属于泊松流到达方式,且各个信号长度随机,故信号到达系统的时间间隔与服务时间均服从负指数分布[9].由于LTE-M系统的最大吞吐量为固定值,因此多个信号同时传输的过程可等效为单一信号在最大吞吐量的情况下依次进行传输.因为LTE-M为车载信息服务的数量m是有限的,当同时为A个信息服务时,系统中潜在的信号数量即减小A个,所以采用系统容量为m的闭合服务方式.因此,本工作将通信模型简化为M/M/1/m/m的排队论模型.

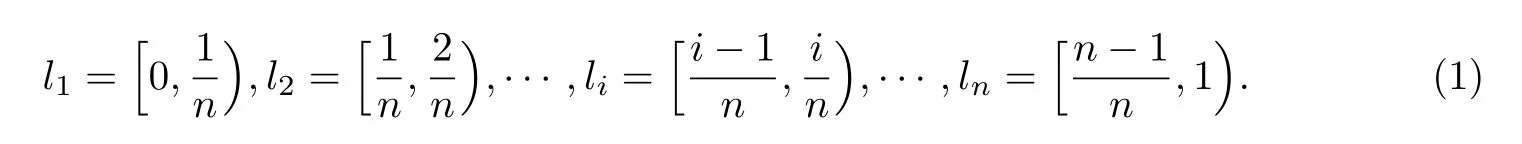
假设在一个单位时间内,取一个很大的自然数n,将单位时间[0,1)分为等长的n段,由式(1)可知,当n趋向于无穷大时,每个时间段li趋向于无穷小.设同一时间段内列车不可能同时发生两次信号传输请求,并设每个时间段li内发生信号传输请求的概率相等,则单位时间内信号传输请求的次数即为li的个数.

设数据通信系统在每个通信周期T内发送信号m次,则每个信号的接入率,每个信号在任意一个时间段li内发生传输请求的概率为.若在任意时刻,系统内正在服务的信号数量为j,则此时系统在任意一个时间段li内发生信号传输请求的概率为.假设所有信号的平均传输时间长度为τm,则该系统内信号的服务率,即在任意一个时间段li内,系统传输完毕一个信号的概率为.系统内正在服务的信号数量的马尔科夫链如图2所示[10-11],其中表示一个时间段li的长度.

图2 LTE-M用于CBTC数据通信信号排队模型Fig.2 Data queuing model of LTE-M in CBTC

由上述马尔科夫链运算可得

式中,P表示当前系统中正在传输和等待的信号总数为n的概率.利用正则性条件=1,n可得

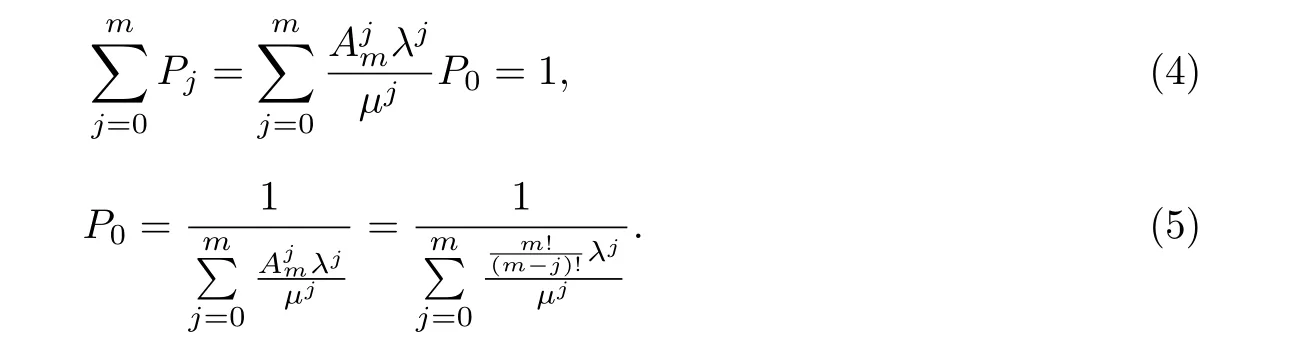
将式(5)代入式(3),可得

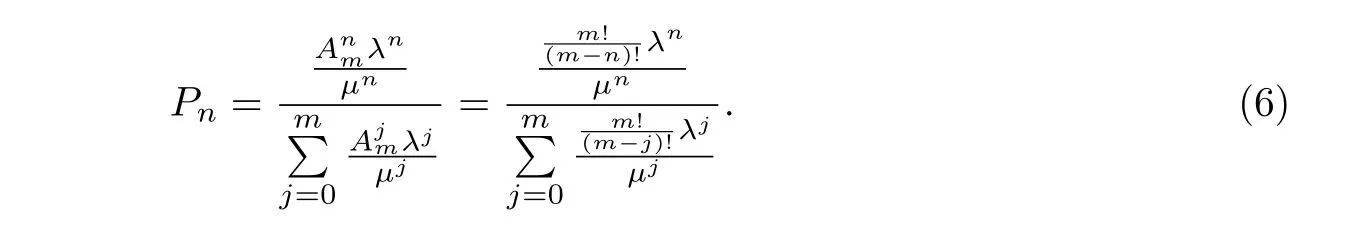
1.3 信号等待时间

基于上述模型,系统只有两种状态:传输信号状态与空闲状态.系统在周期T内共传输信号m次,平均每次传输时长的均值为τm,则在一个周期T内系统正在传输信号的时长为mτm.当信号接入请求发起时,若当前系统处于传输状态,则该信号发生时延.因此,发生时延的概率Pτ为除该信号外其余信号的总传输时间与一个周期的总时间之比,即

当某信号发起接入请求时,若系统状态空闲,则直接接入,这意味着系统空闲时的每一个时间段li内每一个信号的接入概率均为.当信号请求发起时,若系统正在传输其他信号,则该请求会等待至信号传输完成时再接入,这意味着一个周期T内共有m个时间点,因其完成了一段信号的传输,其信号的接入概率Pin将会是过去一段时间内的累加,即为一个周期内发生等待的信号个数除以传输完毕某一信号的时间点总数,即

则在一段时间t内,系统一直保持传输信号状态的概率为

式(11)即为信号接入时等待时间超过t的概率.对1−Ptr进行微分,则等待时间的概率密度函数为

2 仿真验证

2.1 不同带宽下传输数据流的时延

列车位于小区边缘是一种最不利的情况,此时通信信号最弱,LTE自适应地选择正交相移键控(quadrature phase shift keying,QPSK)调制方式,每个子载波携带2 bit信息.在频域上,LTE一个资源块(resource block,RB)占用频宽180 kHz,包含12个子载波频段,每个子载波占用频宽为15 kHz;在时域上,每个时隙为0.5 ms,每个时隙每个子载波频段可传输7个子载波.因此,QPSK调制下LTE系统的理论最大吞吐率为

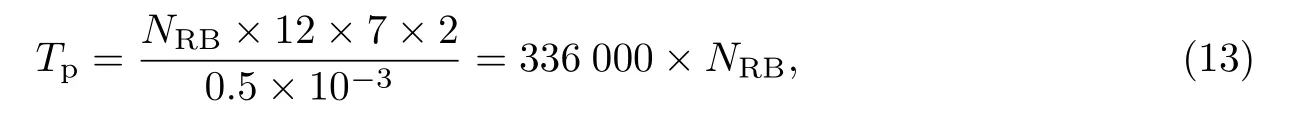
式中,NRB为LTE系统的RB数量.在5 MHz以内的带宽下,对应的RB数量与QPSK调制下的吞吐率Tp如表1所示.

表1 LTE系统对应的RB数量与QPSK调制下的吞吐率Table 1 Number of RBs and rate of throughput in QPSK modulation in LTE system

根据CBTC数据通信实际需求,以及无线设备商与信号公司提供的相关数据,设置系统最大传输单元(maximum transmission unit,MTU)为1 500B(数据包超过该值则分片传输),所有数据包平均大小为1110B,单小区6辆车数据流量共(512+512)×6=6 144 kbit/s.设置相应情况下信号的接入率λ为平均数据包大小与CBTC系统单小区总数据流量比值的倒数,信号的服务率µ为每个数据包传输时间平均值的倒数.设置系统带宽为5 MHz,单车单路数据流发送512 kbit/s,此时有λ=0.691 9,µ=0.945 9.仿真结果与理论计算结果的对比如表2所示.图3为5 MHz带宽下当λ与µ变化时等待时间的概率密度曲线变化情况.

表2 5 MHz带宽单车单路512 kbit/s数据流量时仿真结果与理论值的对比Table 2 Contrast of data delay simulation results and theoretical value in 5 MHz band width with 512 kbit/s data traffic in single vehicle single link

图3 5 MHz带宽不同λ和µ参数下信号等待时间仿真结果与理论值的对比Fig.3 Contrast of data delay simulation results and theoretical value in 5 MHz band width with different parameter λ andµ

设置系统带宽为3 MHz,当单车单路数据流发送512 kbit/s时,系统不能承载此数据量,因此将数据量减少为256 kbit/s,此时有λ=0.345 9,µ=0.567 6.仿真结果与理论计算结果的对比如表3所示.图4为3 MHz带宽下当λ与µ变化时等待时间的概率密度曲线变化情况.

表3 3 MHz带宽单车单路256 kbit/s数据流量时仿真结果与理论值的对比Table 3 Contrast of data delay simulation results and theoretical valuein 3 MHz band width with 256 kbit/s data traffic in single vehicle single link

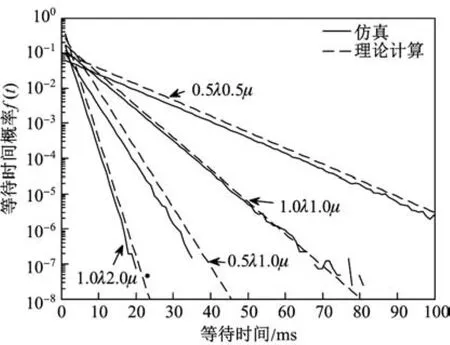
图4 3 MHz带宽不同λ和µ参数下信号等待时间仿真结果与理论值的对比Fig.4 Contrast of data delay simulation results and theoretical value in 3 MHz band width with different parameter λ andµ

设置系统带宽为1.4 MHz,当单车单路数据流发送512,256 kbit/s时,系统均不能承载此数据量,因此,将数据量减少为128 kbit/s,此时有λ=0.173 0,µ=0.227 0.仿真结果与理论计算结果的对比如表4所示.图5为1.4 MHz带宽下当λ与µ变化时等待时间的概率密度曲线变化情况.

表4 1.4 MHz带宽单车单路128 kbit/s数据流量时仿真结果与理论值的对比Table 4 Contrast of data delay simulation results and theoretical value in 1.4 MHz band width with 128 kbit/s data traffic in single vehicle single link

图5 1.4 MHz带宽不同λ和µ参数下信号等待时间仿真结果与理论值的对比Fig.5 Contrast of data delay simulation results and theoretical value in 1.4 MHz band width with different parameter λ andµ

2.2 信号等待对CBTC系统性能的影响

分别设置系统带宽为5.0,3.0,1.4 MHz,系统流量为上下行各512 kbit/s的1,1/2,1/4倍,寻找各个带宽可以承载的最大数据流量,并对信号发生等待的概率与大于150 ms等待时间的概率进行理论计算与仿真统计,结果如表5所示.

由表5可知,当单网为5.0 MHz,数据量为LTE-M规定的单车512 kbit/s时,时延超过150 ms的概率极小,可满足需求;当单网为3.0 MHz时不足以承载数据,但当数据量下降为标准的1/2时,时延满足需求;当单网为1.4 MHz,数据量下降为标准的1/4时,时延超过150 ms的概率小于0.1%,远小于LTE-M规定.

上述分析方法可对工程的部署提供参考.以ZC发送给CC的行驶许可信息为例,设某线路全长30 km,从始发站至终点站运行耗时1 h,平均每1 km布设一个RRU,则列车在每个小区平均耗时2 min.设每个小区内列车在小区边缘行驶20 s为全部时间的1/6.行驶许可信息的周期为0.6 s,假设单网可用带宽为1.4 MHz,单车单路承载CBTC数据流量为128 kbit/s,由表5可知,时延超过150 ms的概率为3.01×10−4,即平均每200 min即会出现一次传输失败.而双网工作时,二者同时发生时延超过150 ms的概率为9×10−8,即平均每11 111 h才会出现一次传输失败.

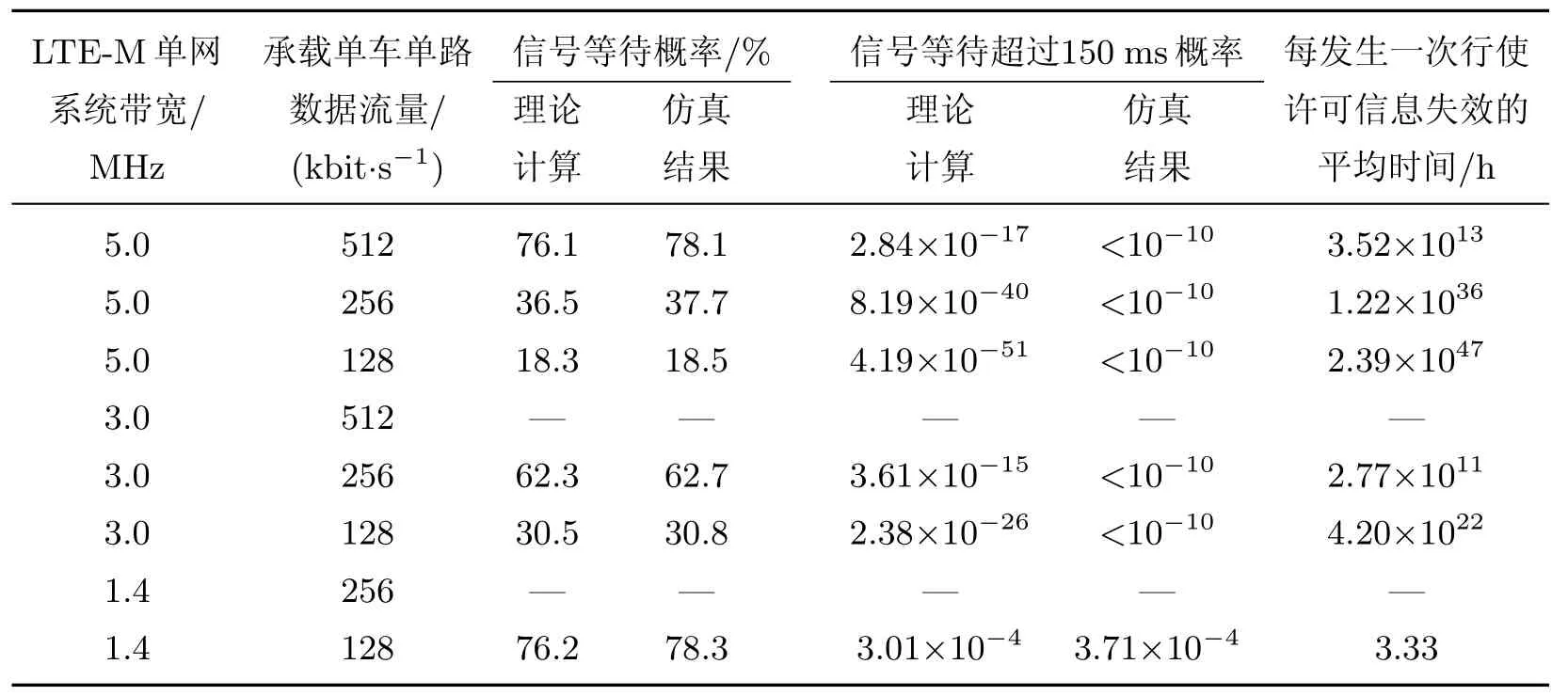
表5 不同带宽承载不同数据流量下信号发生等待的情况Table 5 Results of data delay in different band width and different data traffic

3 结束语

本工作将LTE-M用于CBTC系统数据通信用排队论中的M/M/1/m/m模型对信号时延进行分析,并根据LTE-M规范要求,得出信号等待概率、等待时间的分布与等待时间大于150 ms的概率,以及在不同带宽下LTE-M系统可以容纳的数据流量和相对应超过150 ms时延的概率.结果表明,当单网系统可用频谱资源为5.0 MHz时,可以承载LTE-M用于CBTC数据通信流量标准;当频谱资源为3.0 MHz时,可以承载原标准的1/2;当频谱资源为1.4 MHz时,可以承载原标准的1/4.另外,各个模式下,时延值超过150 ms的概率均可以接受.然而,由于信道的不稳定性以及切换时系统容量减小,仍然有可能发生不可控的通信失败情况.因此,设计应留有余地,确保轨道交通车地通信符合列车运控的要求.