304不锈钢点蚀损伤的非线性超声表征*

李 萍， 陈 雷， 王腾腾， 赵 杰

(大连理工大学材料科学与工程学院 大连,116024)

引 言

不锈钢具有良好的耐蚀性、成型性，在石油化工、航空航天以及核电等领域得到广泛应用。约占不锈钢产量65%～70%的奥氏体不锈钢在含氯离子环境中使用时，合金相、位错露头、空穴等缺陷的存在易引发点蚀(点腐蚀)的萌生[1-3]。虽然因点蚀造成不锈钢的失重很小，但它的破坏性巨大，在实际生产中往往导致腐蚀穿孔直至设备失效[4]。因此，研究奥氏体不锈钢的点蚀问题具有重要意义。

目前，对不锈钢点蚀行为的研究通常采用电化学方法、声发射技术、化学浸泡法以及扫描探针显微技术等。其中：电化学阻抗谱、动电位极化曲线测试和电化学噪声技术可用来进行不锈钢点蚀损伤的早期检测[5-7]，但检测效率低，且对材料存在破坏性；激光共聚焦扫描显微镜和扫描电化学显微镜技术可较好地对点蚀孔的发展状态进行微观测量、观察和分析，但是不便于宏观统计分析[8-9]；声发射技术对材料中的弹性波敏感，可有效反应材料服役过程中的变化，但检测时极易受到机电噪声的干扰[10]；脉冲涡流检测[11]可得到包括缺陷深度、宽度等丰富的缺陷信息，并进行定量检测，但对不锈钢点蚀早期并不敏感[12-14]；传统超声检测技术可对材料性能进行无损表征与评价，但检测灵敏度过低[15-16]。

含有界面、微裂纹和不均匀等缺陷的材料本身都具有非线性效应，它们与超声波相互作用后会产生相应的非线性响应信号，这种非线性效应极其微弱，不足以通过常规超声方法检测出来，但是，这些非线性效应却包含反映材料状态的重要信息，非线性超声检测技术便是通过分析非线性效应响应程度对材料性能进行评价[17]。目前，非线性超声检测技术可作为材料早期疲劳损伤[18]、热损伤[19]、残余应力[20]、应力腐蚀[21]、复合材料黏接强度[22]、损伤定位与识别[23]等有效的表征与评价方法。

相比超声体波，超声表面波具有传播距离更远，适于大工作面的检测；声波能量集中在材料近表面，对近表面的非线性效应更加敏感的优势。因此，笔者提出利用非线性超声表面波检测技术对304不锈钢点蚀损伤进行研究。将固溶态304奥氏体不锈钢试样，在质量分数为6.0%,10.0%,14.0%的FeCl3溶液中分别浸泡6,12,18 h，观察试样表面微观形貌、统计稳态点蚀孔尺寸、测量试样的超声表面波非线性系数；基于非线性超声理论分析304不锈钢试样点蚀损伤与超声表面波非线性系数的相关性，探讨以非线性超声表面波研究304不锈钢点蚀损伤的可行性。

1 超声表面波非线性检测理论基础

超声表面波在固体介质自由表面传播过程如图1所示，x轴为自由表面水平方向，z轴方向为半空间固体材料的深度方向[24]。

表面波在介质表面传播时，表面层质点振动具有纵波和横波叠加的综合特性，相应的纵波和横波的位移势函数可表达为

(1)

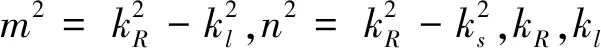
根据固体介质半空间自由表面边界条件可得

(2)

由于超声表面波是由纵波和横波叠加组成的，那么，就可以将该超声表面波的位移进行横、纵向的分解，其表达式为

(3)

对于具有微弱二次非线性的固体介质，超声表面波在其近表面传播足够远的距离后，将会产生相应的二次谐波。此时，超声表面波的位移在横、纵方向可分解[25]为

(4)

对于各向同性材料，由于三阶弹性常数的对称性，材料的超声表面波声学非线性仅仅与纵波有关。因此，对于在该种固体介质材料近表面传播的表面波来说，其基频波幅值和倍频波幅值的比值关系可用纵波中的基频波幅值和倍频波幅值[26]来表示，即

(5)

其中:β为纵波的声学非线性系数;x为纵波的传播距离。

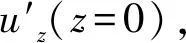
(6)

根据式(6)可将固体介质近表面质点的位移分量与纵波声学非线性系数之间的关系表达为

(7)

对于上式中的波数k，其与波长λ、声速c、频率ω的关系表达式为

k=2π/λ=2πω/c

(8)

式(8)代入式(7)，化简可得

(9)

其中：u2ω,uω分别为基频波和倍频波幅值。

(10)

其中:x为超声表面波传播距离;cL，cS和cR分别为纵波，横波和表面波的声速。

另外，将式(9)改写为

(11)

其中:A2，A1分别为基频波和倍频波的幅值；β为超声表面波相对非线性系数。

为了研究方便，传播距离x确定时，定义非线性系数[27]

(12)

通过式(11),(12)可看出，相对非线性系数β′与绝对非线性系数β成正比。因此，在表面波传播距离一定的情况下，可用β′表征β。

2 实验材料和方法

2.1 样品制备

实验材料为304奥氏体不锈钢冷轧钢板，化学成分见表1。通过线切割加工10 mm×10 mm×3 mm(A)及100 mm×20 mm×8 mm(B)两种规格的试样若干。将两种规格的所有样品同时进行固溶处理，然后打磨，抛光；石蜡封装试样，密封胶涂覆缝隙，最后预留出100 mm2的工作面，充分固化后进行化学浸泡实验。其中A规格样品用以点蚀形貌、点蚀孔尺寸的观察；B规格样品用于304不锈钢点蚀损伤的超声表面波非线性实验。浸泡实验所用FeCl3溶液质量分数为6.0%,10.0%,14.0%；浸泡时间为6,12,18 h。

表1 304不锈钢的化学成分(wt%)

Tab.1 Chemical composition of 304 stainless steel (mass fraction/%)

成分FeCr Ni MnPSSiC含量Bal17.588.011.180.0350.0290.510.035

2.2 非线性超声表面波检测系统

实验所用非线性超声表面波检测系统如图2所示。

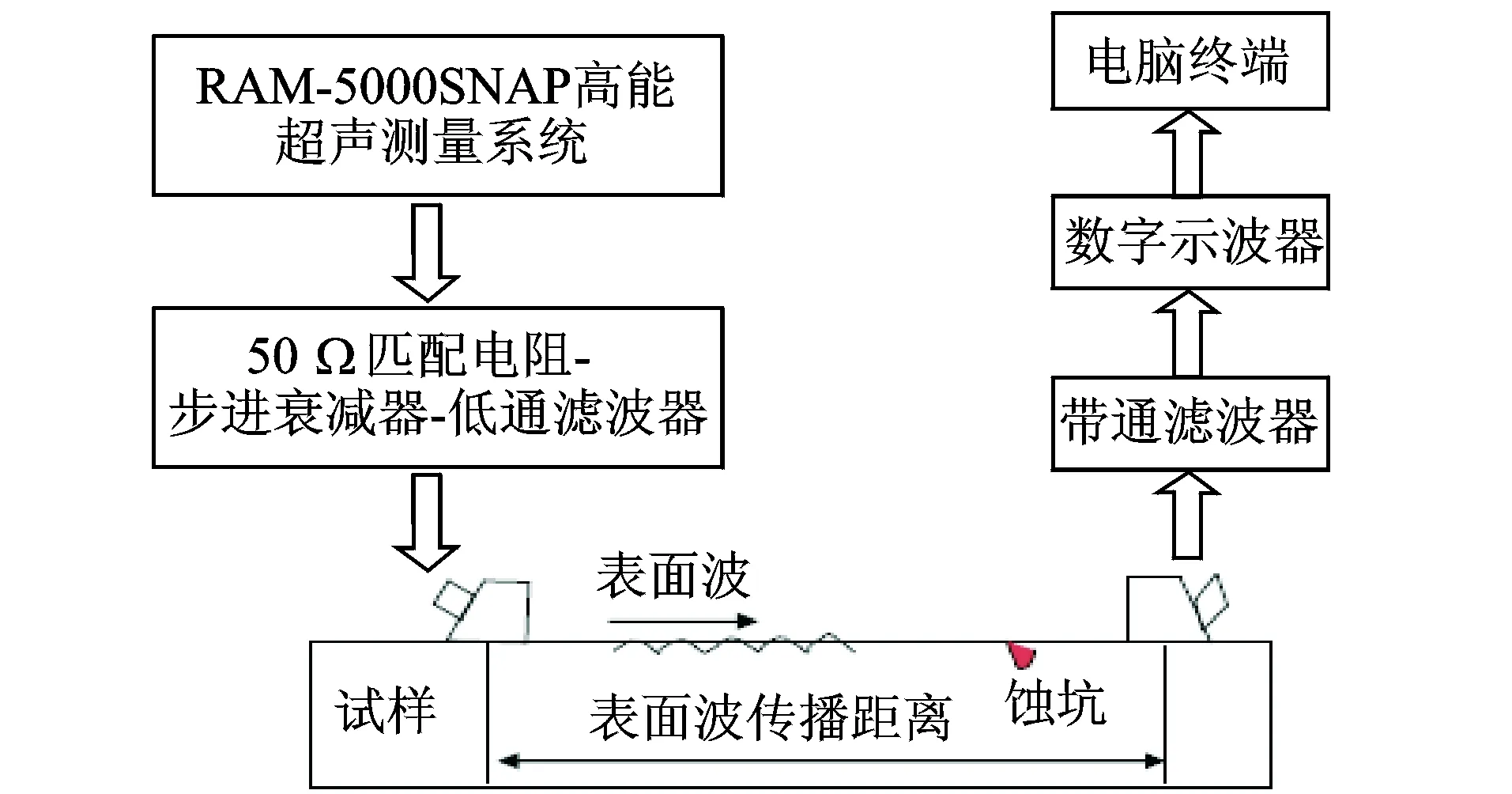
图2 非线性超声表面波检测系统示意图Fig.2 Schematic diagram of nonlinear ultrasonic surface wave detection system

固定超声表面波传播距离时，使得表面波通过点蚀区域，每个试样进行5次重复测量，取5次测量的平均值作为最终检测结果。最后，对得到的浸泡试样的相对非线性系数β′与固溶态试样的相对非线性系数β0′进行归一化处理。

2.3 点蚀微观形貌观察及稳态蚀孔尺寸统计

利用日本奥林巴斯(OLYMPUS)公司生产的OLS4000激光共聚焦显微镜对304不锈钢浸泡试样进行表面形貌的观察、稳态点蚀孔三维形貌以及稳态点蚀孔尺寸的测量，分析并讨论实验条件下304不锈钢点蚀损伤特征的演变。考虑到点蚀的随机性，对每个点蚀状态进行不少于3个视场的观察，对每个蚀坑进行不少于5次的直径和深度测量与统计处理，取平均值作为最终检测结果。

3 实验结果与分析

3.1 浸泡试样表面形貌观察

浸泡试样的表面点蚀形貌如图3所示。观察发现：在质量分数为6%的FeCl3溶液中，浸泡初期(6 h)试样表面存在明显的局部腐蚀，稳态点蚀孔直径较小，且周围散布少量弱点蚀孔；随着浸泡时间的延长(12,18 h)，稳态点蚀孔直径变大，点蚀孔数目增多；当质量分数增加到10%以后，试样表面的稳态点蚀孔形状变得不规则且随着浸泡时间的延长，稳态点蚀孔尺寸增大更加显著；继续增大溶液的质量分数到14%时，随着浸泡时间的延长，点蚀孔总量明显增多，但稳态点蚀孔的尺寸变化较小。综上所述，随着浸泡时间的延长和溶液质量分数的增大，304不锈钢试样在FeCl3溶液中的点蚀损伤趋于严重，这与点蚀的自催化理论相一致。

图3 蚀孔表面形貌 (左：6 h；中：12 h右；18 h)Fig.3 Pitting pore surface morphology (left:6 h；middle:12 h；right:18 h)

3.2 浸泡试样稳态蚀孔尺寸统计

用激光共聚焦显微镜对在质量分数为14%的FeCl3溶液中浸泡14 h的试样进行稳态点蚀孔深度和直径测量，其扫描形貌如图4所示。

图4 点蚀深度测量示意图Fig.4 Schematic diagram of pitting depth

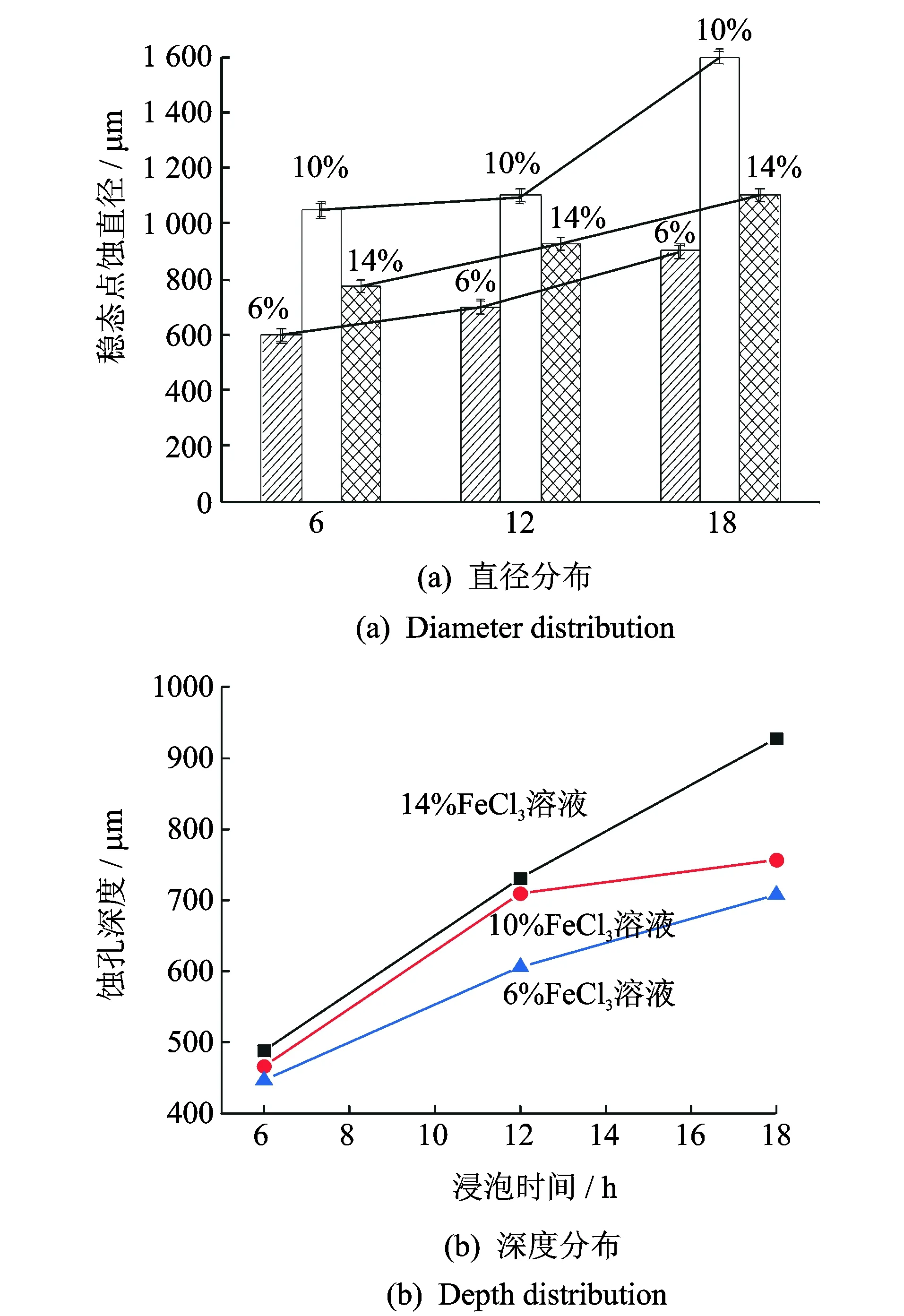
图5 稳态蚀孔统计结果Fig.5 Statistical results of steady pitting

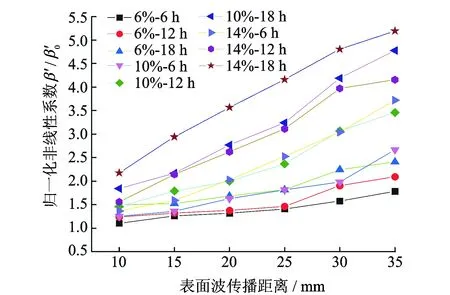
图6 归一化非线性系数随表面波传播距离变化Fig.6 Variation of normalized nonlinear coefficient with surface wave propagation distance

通过上述方法对所有浸泡试样进行测量，稳态点蚀孔直径和深度统计结果如图5所示。由图5(a) 可得，相同浸泡时间下，在质量分数为10%的FeCl3溶液中，单个稳态蚀孔的直径最大，且浸泡时间越长、溶液质量分数越大，大小差别越显著；图5(b)的稳态点蚀孔深度分布统计可知，在质量分数相同的溶液中，样本点蚀孔的深度随着浸泡时间的延长而增大；同一浸泡时间下，溶液质量分数越大，稳态点蚀孔的深度越大。通过浸泡试样点蚀形貌观察及稳态蚀孔尺寸的统计，在一定程度上能够说明随浸泡时间的延长和FeCl3溶液质量分数的增大，溶液中304不锈钢试样的点蚀损伤有加重的趋势。

3.3 不锈钢点蚀损伤的超声非线性表征

图7 归一化非线性系数变化Fig.7 Variation of normalized nonlinear coefficient

图6为不同表面波传播距离下，点蚀损伤的归一化非线性系数(β′/β0′)随浸泡溶液质量分数(6%，10%，14%)和浸泡时间(6,12,18 h)的变化曲线。随着超声表面波传播距离的增加，归一化非线性系数在整体上呈现单调递增的趋势，且随着点蚀程度的加剧愈加显著；传播距离一定时，浸泡时间越长、溶液质量分数越高，归一化非线性系数上升幅度越明显；当超声表面波传播距离范围为15～25 mm时，归一化非线性与传播距离的线性拟合相关度约为97.327 5%～99.999 3%，因此，可以采用该距离范围内的归一化非线性系数对浸泡试样的点蚀损伤进行非线性超声表征。超声表面波传播距离分别为15,20,25 mm时，浸泡试样不同处理状态下的归一化非线性系数变化如图7所示。由图可看出：浸泡时间一定时，归一化非线性系数全部随着溶液质量分数的增加而逐渐增大；溶液的质量分数一定时，浸泡试样的归一化非线性系数全部随着浸泡时间的延长而变大，且时间越长，非线性系数增长率越大。综上可知，归一化非线性系数与304不锈钢试样的点蚀损伤状态具有一定的相关性。

3.4 分析与讨论

研究表明，有限幅度超声波在材料中传播时产生的超声非线性响应信号源自于经典声非线性和接触声非线性，其中：经典声非线性主要与材料晶格的非简谐性和晶体缺陷(畸变)有关，它具有分布性的特点；而接触声非线性则与裂纹、界面和接触面的应力-应变非线性有关，反映了材料的局部缺陷特征，缺陷的存在将导致超声波与其相互作用时发生强非线性失真[28]。如前所述，304不锈钢试样发生点蚀损伤后，试样表面生成稳态点蚀孔，这使得材料的界面连续性遭到破坏。因此，当有限幅度的超声波作用于这种不连续界面时，声波的质点振动会迫使不连续界面产生变形，界面两侧会在超声波的作用下表现出很强的运动非线性，即界面的应力-应变关系产生非对称性，该应力-应变的非线性会导致部分超声入射能量转移到谐波信号中，表现为高频谐波信号的形成。其中，二次谐波的幅值[29]可表示为

(13)

其中：A1为基频波幅值；A2为二次谐波幅值；k=ω/c为波数；x为传播距离，E1和E2分别为二阶、三阶弹性常数。

E1，E2与应力、应变密切相关

σ=Ε1ε+1/2Ε2ε2

(14)

其中：ε为应变，σ为应力。

联系式(13)，(14)可以得出，二次谐波的幅值与材料的应力-应变非线性成正相关，即应力-应变非线性越显著，材料的二次谐波幅值越大。通过不锈钢点蚀试样的表面微观形貌(图3)和点蚀孔的尺寸变化(图5)可知，随着溶液质量分数的增大和浸泡时间的延长，不锈钢试样点蚀损伤程度加大，表现在试样表面点蚀孔增多、点蚀孔尺寸显著增大，导致材料的不连续界面面积增大。因此，可利用相对非线性系数描述蚀孔处界面不连续性引起的超声表面波非线性效应

(15)

其中：β′为超声表面波相对非线性系数；β为超声表面波绝对非线性系数；f(ω)为频率的函数。

试样表面存在的点蚀会使表面波传播距离x变大、材料的不连续界面面积增多，造成声波与界面的相互作用变大，界面间的应力-应变非线性效应增强，而二次谐波的幅值又与界面间的应力-应变非线性相关，304不锈钢试样点蚀损伤的加重会产生更强的二次谐波，文中表现为归一化非线性系数的增大。因此，在表面波传播距离一定的情况下，利用超声表面波非线性表征304不锈钢的点蚀损伤是可行的，即点蚀损伤越严重，超声表面波非线性效应越显著，归一化非线性系数越大。

4 结束语

利用非线性超声表面波检测系统对304不锈钢进行点蚀损伤的探究，结果显示：非线性效应随表面波传播距离的增大而具有累积效应；随浸泡时间的延长、溶液质量分数的升高，归一化非线性系数β′/β0′变大。利用激光共聚焦显微镜技术对304不锈钢试样点蚀形貌的观察以及稳态蚀孔尺寸和失重率的测量统计，发现延长浸泡时间和增加溶液质量分数后，试样的点蚀发展更加迅速，点蚀损伤愈加严重。304不锈钢点腐蚀损伤过程中非线性系数的变化归因于超声波与点蚀引起的304不锈钢不连续界面相互作用，造成界面间的应力-应变非线性效应，且非线性效应随点蚀损伤的加剧趋于显著。