康复机器人准零刚度隔振特性分析与实验*

杨雪锋， 孟庆国， 李 威， 路 恩， 盛连超， 董 事

(中国矿业大学机电工程学院 徐州， 221116)

引 言

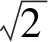
对于被动隔振技术的研究具有非常重大的意义，它在精密工程、超精密工程[29]、车用发动机[30]、船舶[31-32]领域有广泛的应用。基于正负刚度并联的隔振原理，笔者采用拉伸弹簧作为负刚度机构与线性正刚度弹簧并联，设计出一种新型的准零刚度隔振系统，它对轻型机器人，特别对足式机器人低频振动具有较好隔振性能。运用静力学特性，分析了系统在静力平衡位置附近的准零刚度特性；通过动力学特性研究，建立了系统分别在简谐力和简谐位移激励下的非线性动力学方程，应用谐波平衡得到系统的力传递率和位移传递率;通过数值仿真观察有、无负刚度情况下隔振系统的输入、输出曲线。

1 隔振器三维建模

1.1 三维建模和受力分析

图1(a)为笔者提出具有准零刚度特性的隔振系统。主要包括：①底座、②支撑柱、③滑板、④连杆、⑤载物台、⑥垂直弹簧、⑦滑块及⑧拉伸弹簧。在滑块上安装两个圆柱销，滑块、连杆和水平弹簧通过圆柱销连接。垂直弹簧的两端分别安装在底座和载物台的弹簧安装孔中。在初始位置竖直压力等于零，载物台存在一个初始高度，当施加载荷后，载物台同时受到垂直弹簧与拉伸弹簧的作用力。对于此准零刚度隔振机构，垂直弹簧主要用来承载静态质量，而图中对称的两个水平拉伸弹簧即为负刚度机构，可以和垂直正刚度弹簧的刚度相抵消。图(b)则为三维图简化的受力分析，其中：F为受力；x为垂直方向位移；θ为连杆与水平线的夹角；L0为拉簧1/2的长度；h0为初始高度；Ks拉簧刚度；L为旋转杆长度。

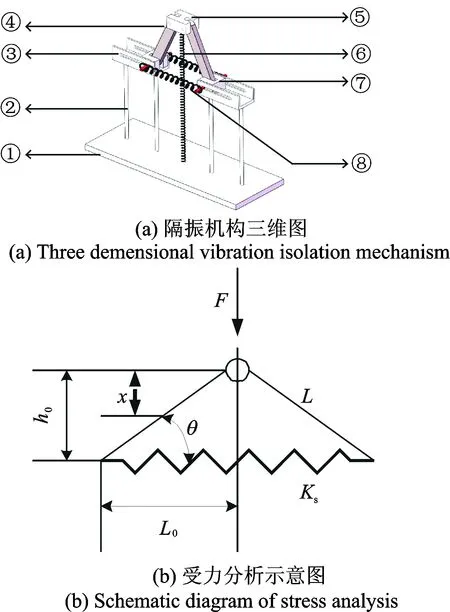
图1 隔振三维模型和受力分析Fig.1 Isolation model and stress analysis

1.2 负刚度机构

如果不考虑垂直弹簧，负刚度机构一侧的受力分析如图1(b)所示。载物台承载一定质量的物体后，根据几何关系，取其中一个拉伸弹簧的1/2部分作受力分析，求出在垂直方向上力F的表达式为

F=4Fstanθ

(1)

其中：Fs=Ksλ为拉伸弹簧1/2部分的水平力；λ为拉伸弹簧1/2部分被拉伸的距离。

在任意位置，夹角θ的表达式为

(2)

其中

将式(2)～(4)带入式(1)，此负刚度的回复力为

(5)

对式(5)进行无量纲化处理，即方程两侧同时除以KsL0得到

(6)

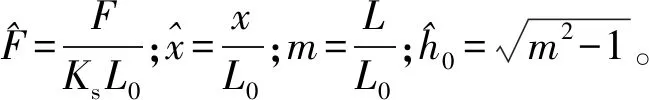
式(6)即为本隔振系统负刚度机构的无量纲力-位移的表达式，由此可以得到它的曲线图，如图2(a)所示。参数m的不同取值对此机构是否存在负刚度特性有一定影响，当m=1时，无量纲力总是随

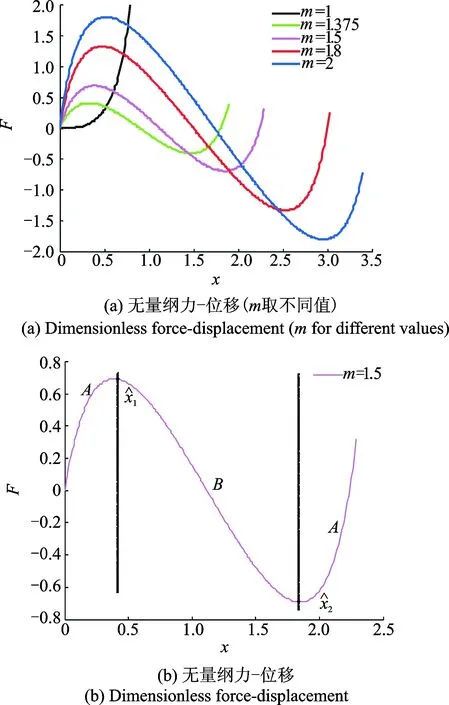
图2 无量纲力-位移图Fig.2 Dimensionless force displacement diagram

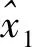
综上，若忽略竖直弹簧的影响，整体机构的回复力近似一条三阶曲线，如图2所示，回复力有可能小于零，而当回复力小于零时，如图2(b)所示，机构刚度大于零或小于零，若刚度小于零，就失去了隔振的意义，也达不到准零刚度隔振的效果。因此，添加竖直弹簧是必要的。

2 静力学特性

针对足式机器人行走时，来自地面的低频振动对其工作性能的影响，提出负刚度机构与刚度为Kv的线性正刚度弹簧并联，构造出一种新型的准零刚度隔振系统，实现机器人足部对低频振动的衰减，设计如图3所示。

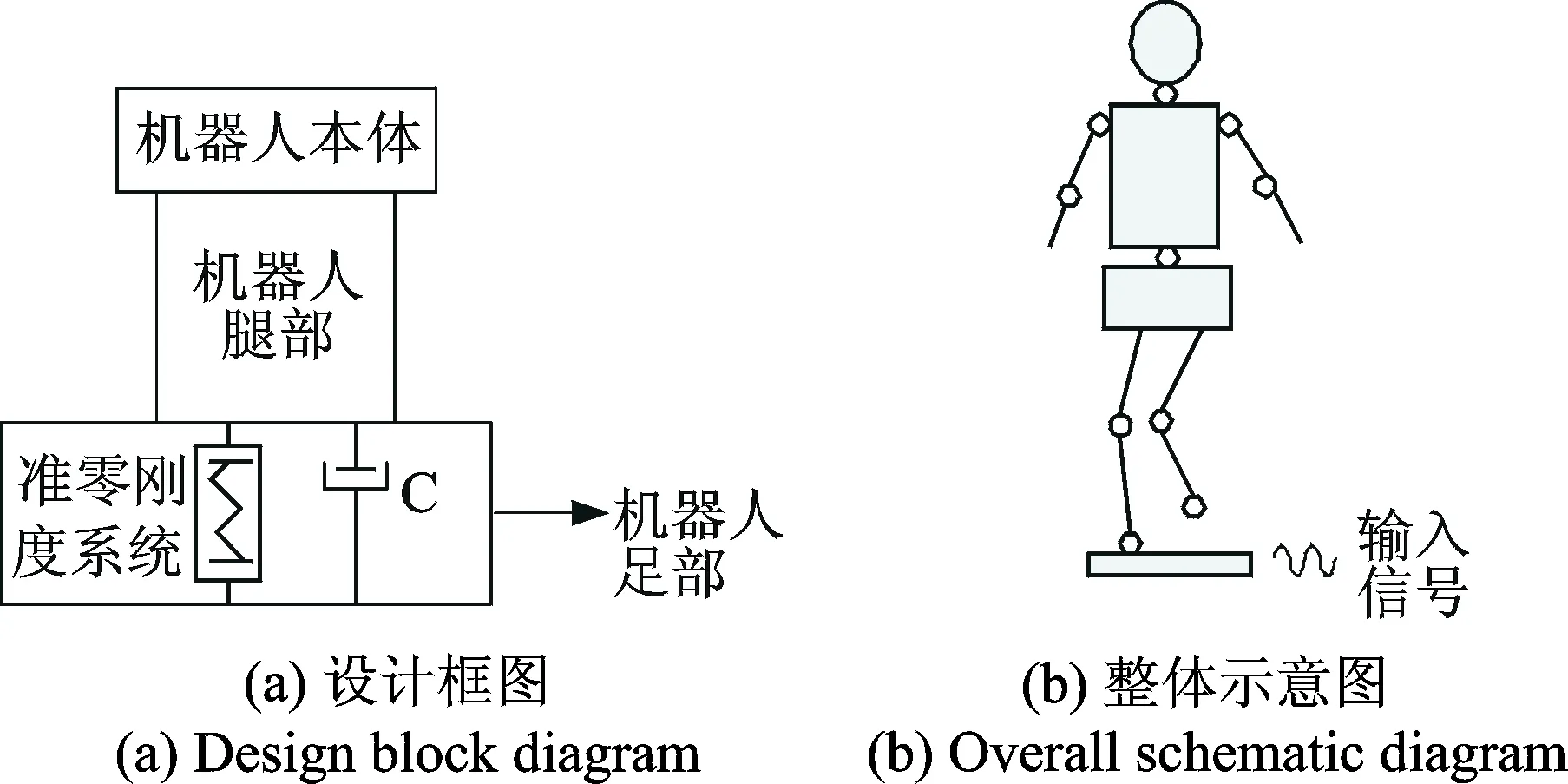
图3 机器人准零刚度隔振设计框图与整体示意图Fig.3 Block diagram of robot quasi-zero-stiffness vibration isolation and whole sketch map

若将机器人足部抽离出来，主要分析准零刚度隔振器。假设在竖直力F的作用下，

由图1可知此

准零刚度隔振系统的无量纲力-位移关系式表示为

(7)

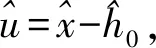
(8)

其中:α=Ks/Kv为刚度比。

对式(8)进行求导，得到系统无量纲刚度-位移的关系

(9)

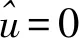
(10)

(11)

结合式(9)～(11)可以得出系统在平衡位置处不同参数值的准零刚度特性，如图6所示。根据图6可知，在m不断增大的情况下，则需要更小的刚度比α使其在平衡位置保持零刚度特性。

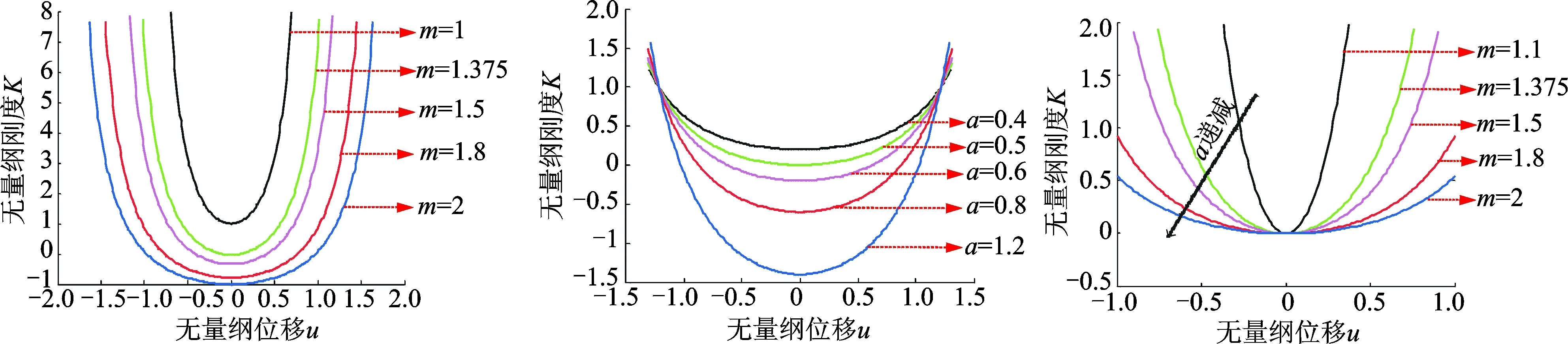
图4 不同m值下的刚度曲线 图5 不同刚度比下的刚度曲线 图6 参数不同时无量纲位移-刚度 Fig.4 Stiffness curves under Fig5 Stiffness curves under different Fig．6 Non dimensional displacement- different m values stiffness ratios stiffness for parameter

3 动力学特性

3.1 回复力近似替换

为方便研究系统动力学特性，需对其数学模型进行简化，即系统回复力可以用一个三阶表达式近似替换。通过泰勒展开式并忽略高次项，来近似替换回复力。

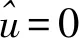
(12)

所以，无量纲力-位移近似关系式为

(13)

(14)

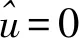
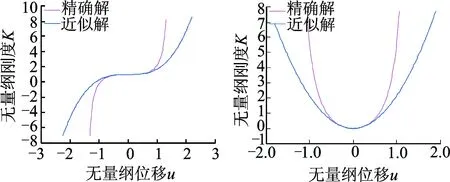
图7 精确力和近似力比较 图8 精确刚度和近似刚度比较Fig．7 Precision force and approximate force comparison Fig.8 Comparison of exact stiffness and approximate stiffness

3.2 系统动力学建模

当承载被隔振物体后，刚好u=0，达到静力平衡位置，此时系统的刚度等于零。由式(8)知

(15)

对该系统施加两种谐波激励，分别是对隔振物体进行谐波力激励Fcos(ωt)，对基座施加谐波位移激励Zcos(ωt)并建立系统的非线性运动微分方程

其中：y=u-z为谐波位移激励下被隔振物体与基座之间的相对位移；F1和F2为谐波力激励与谐波位移激励下的系统回复力。

则

(18)

(19)

(20)

(21)

为方便表达，将式(20)，(21)统一化成

(22)

(23)

由式(23)可以解出在谐波力和谐波位移激励下的关于Ω的两个解，其表达式为

(24)

(25)

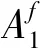
(26)

(27)

设fe，fd为弹性力和阻尼力，通过准零刚度隔振系统传递到基础上的力为

(28)

它的力传递率为

/F

(29)

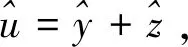
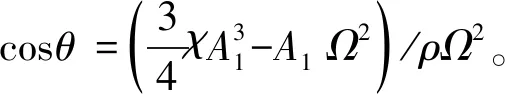
根据以上分析，可以得到不同的激励幅值和参数对隔振系统的影响，如图9、图10所示。

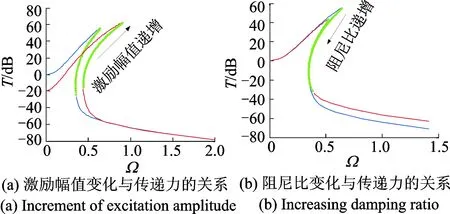
图9 力传递率Fig．9 Force transfer rate

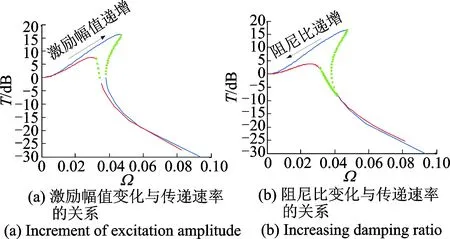
图10 位移传递率Fig．10 Displacement transfer rate

图9为力传递率曲线图，绿色曲线表示非稳定解，(a)(b)图分别为激励幅值与阻尼比变化时对力传递率的影响。由图9(a)知，随着激励幅值的递增，力传递率也是递增的，当激励频率大于一定值后，力传递率会迅速下降，而且，适当提高激励幅值会使系统的隔振起始率降低。由图9(b)知，改变阻尼比并不能降低隔振系统的隔振起始率，随着阻尼比的不断增大，力传递率也随之变大，这与理论符合。

由图10(a)和(b)可以看出，其中，绿色曲线也为非稳定解，无论是激励幅值还是阻尼比对位移传递率的影响基本相同，该系统的激励幅值和阻尼比越小，隔振的频率范围越大，对被隔振物体的损害变小，系统的隔振性能也越好。

4 实 验

4.1 实验装置

实验的激励控制装置主要包括振动控制器(SCS-2 Shaker Control System)、功率放大器(Power Amplifier BAA 120)以及上位机(电脑)。在图11中，连接线除了连接振动控制器和功率放大器外，还将电脑与振动控制器相连，通过电脑安装的VibExpert软件，将在软件VibExpert里输入的激励频率和激振幅值通过功率放大器的放大后，作为准零刚度系统里激振器(S 51110)的输入信号，最终产生输出振幅。

图11 准零刚度隔振实验的激励控制装置Fig.11 Excitation control device of quasi zero stiffness vibration isolation experiment

准零刚度隔振装置主要包括准零刚度机构、被隔振的物体、导向装置以及导杆，准零刚度机构安装在一个底座上，底座安装在激振器上，底座和准零刚度隔振机构可看做一个整体。压簧套在导杆的外围，在避免摩擦的情况下，两者直径相当，导杆可以在振动的时候保证压簧不会弯曲变形。为了减小竖直和水平运动方向的摩擦，装置中都安装了滚轮，因为滚动摩擦力相对较小。

输出位移采集装置主要包括LK-G35激光位移传感器(激光传感头、RS-232C连接器)与LK-Navigator测量软件。LK-G35激光位移传感器的测量范围为-5～+5 mm，它的精确度可以达到微米，通过USB与电脑相连，利用LK-Navigator软件对测量的输出位移量进行记录和处理。

4.2 实验分析

根据以上的理论研究，现对提出的准零刚度隔振系统进行实验台的搭建和实验验证。实验台如图12所示，其中，刚度比为0.97，被隔振质量为1.2 kg。激振器提供振动源，包括振幅和频率。激光位移传感器测量输出的位移。

图12 准零刚度实验台Fig.12 Eperimental platform of quasi zero stiffness

因为康复机器人穿戴于人体上，而人体的敏感频率范围在4～8 Hz之间，实验的激振频率取值为3.0～15 Hz,可以得到在有无负刚度机构下的数据表以及与理论曲线的对比图，如表1和图13所示。然后，在同样的实验环境下，改变激励幅值，得准零刚度传递率的变化曲线，如图14所示。

表1 准零刚度隔振实验数据表

Tab．1 Experimental data of quasi zero stiffness vibration isolation

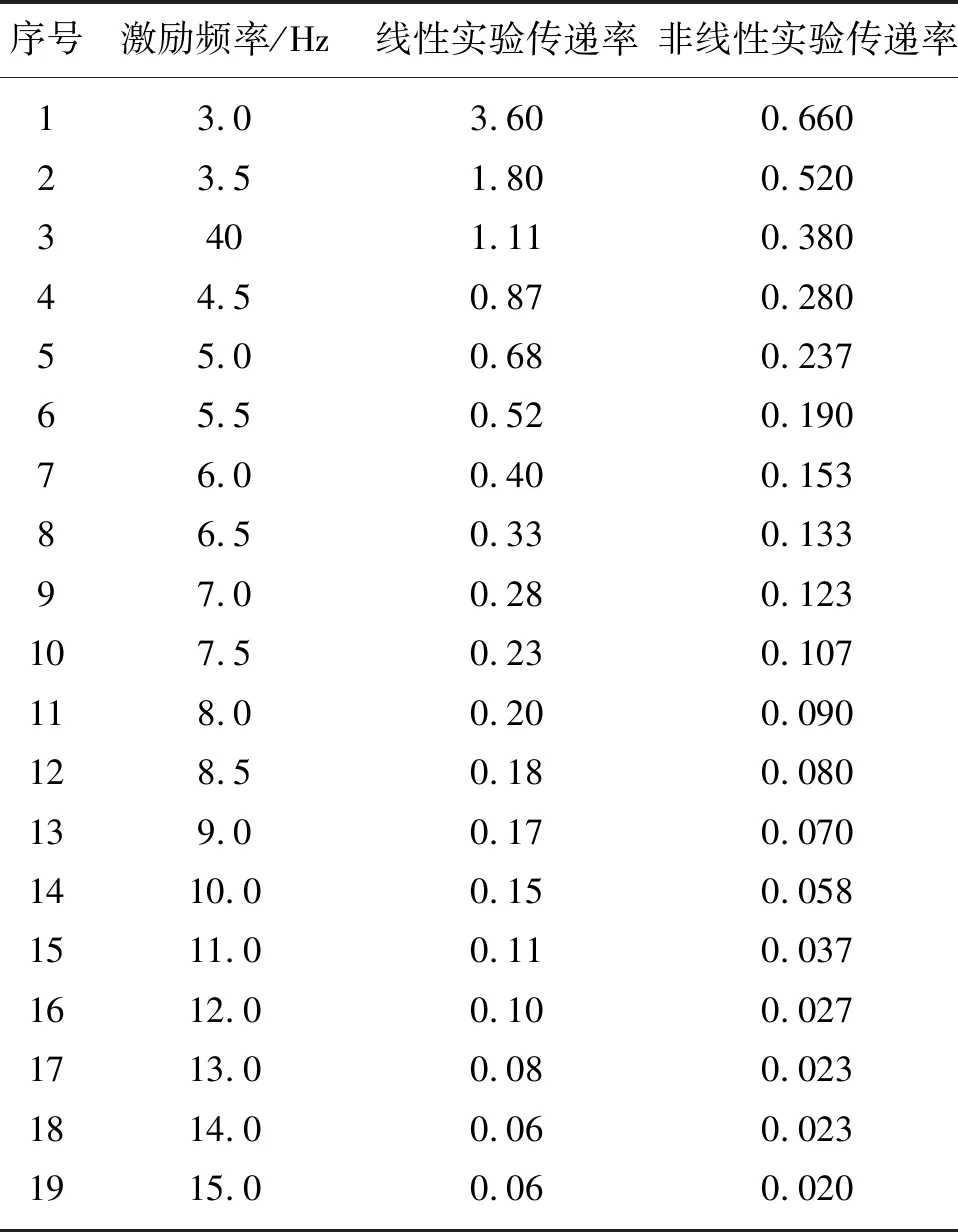
序号激励频率/Hz线性实验传递率非线性实验传递率123456789101112131415161718193.03.5404.55.05.56.06.57.07.58.08.59.010.011.012.013.014.015.03.601.801.110.870.680.520.400.330.280.230.200.180.170.150.110.100.080.060.060.6600.5200.3800.2800.2370.1900.1530.1330.1230.1070.0900.0800.0700.0580.0370.0270.0230.0230.020

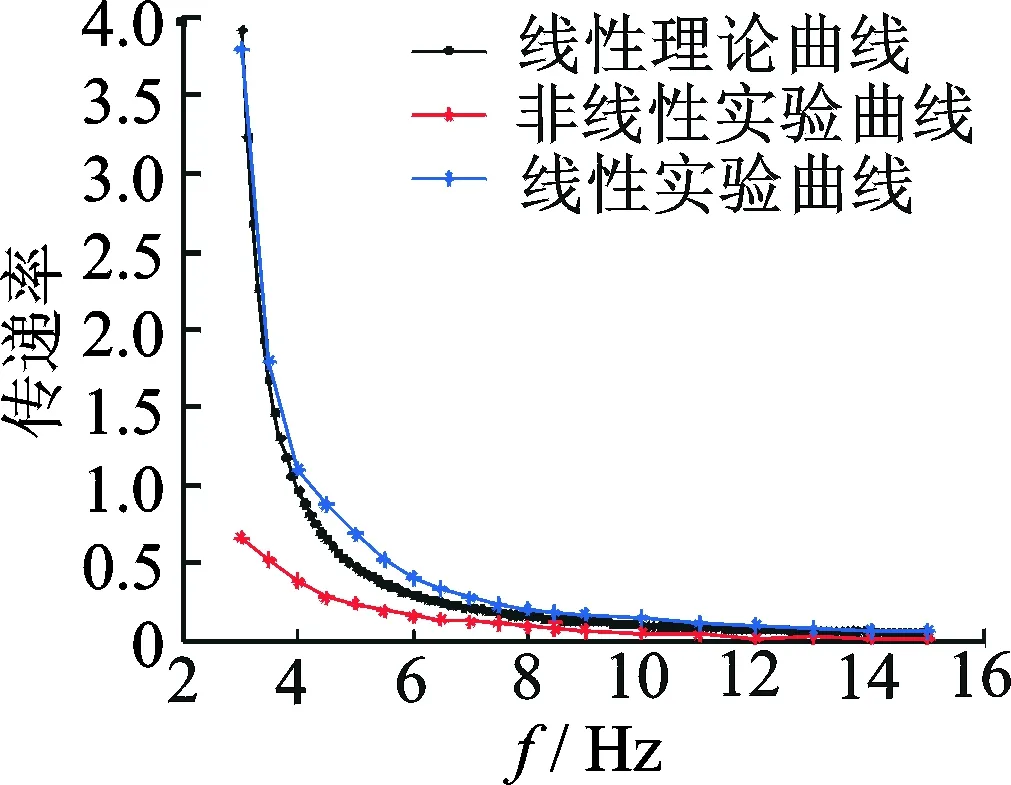
图13 准零刚度实验曲线图Fig.13 Experimental curves of quasi zero stiffness

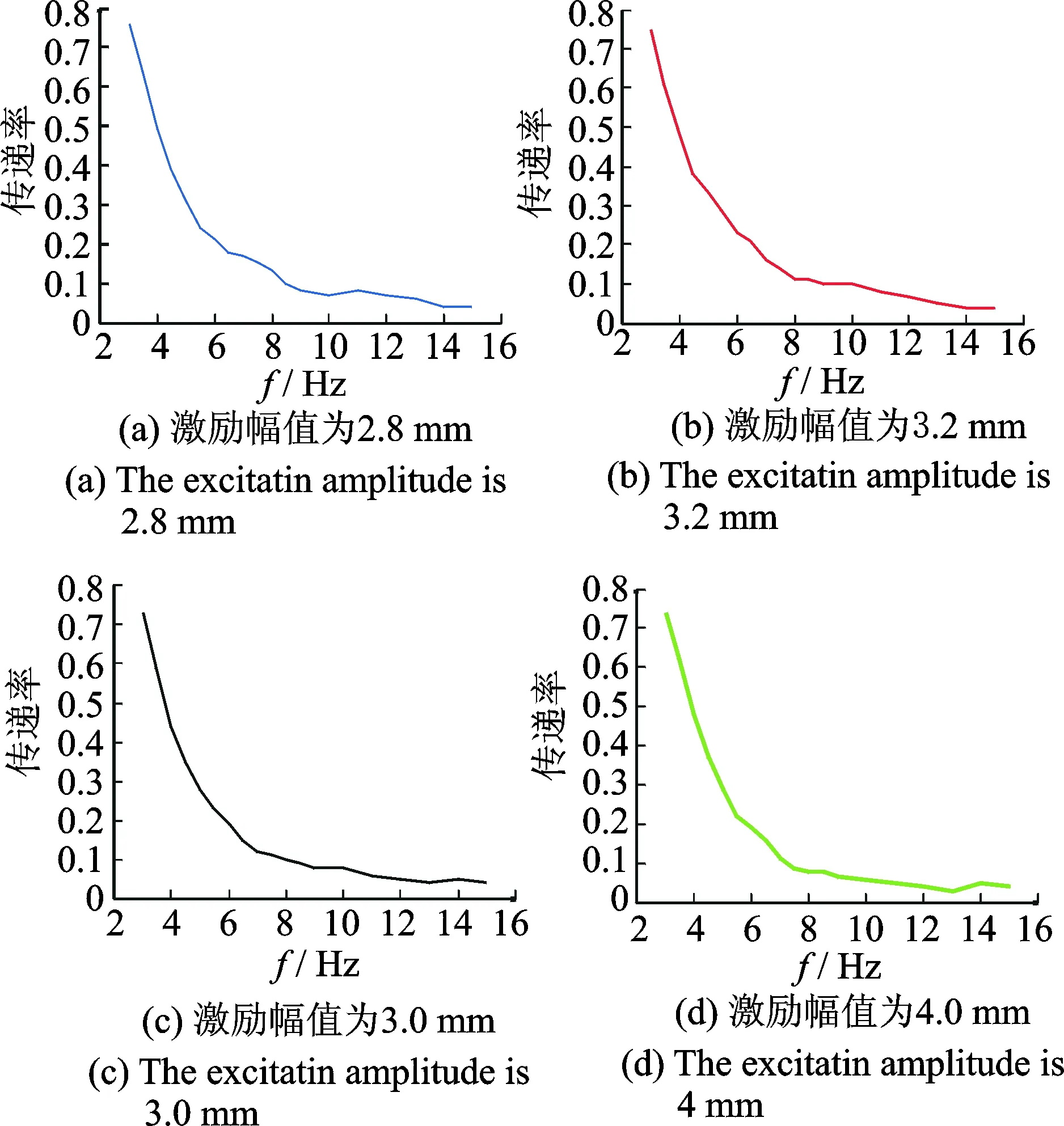
图14 不同激励幅值的准零刚度传递率曲线Fig.14 Quasi-zero-stiffness transfer curve with different excitation amplitude

由图13可知，在频率3～8 Hz之间，隔振系统的传递率存在很大变化，这也说明，此准零刚度隔振系统应用在康复机器人上，能够有效减少低频振动对人体的影响，具有实际意义。其次，对激励幅值改变对隔振系统的影响进行了验证，如图14中，图(a)～(d)代表激励幅值逐渐递增，又因为实验验证并没有达到共振，而是集中在曲线峰值右侧，传递率分别对应0.761,0.755,0.740和0.732，传递率在峰值右侧递减，进一步验证了理论的正确性。

5 结束语

笔者提出了一种以拉簧作为负刚度机构，并与线性正刚度弹簧并联且适用于康复机器人的准零刚度非线性被动隔振系统。研究分析了此系统的静力学、动力学特性并对其隔振性能进行数值仿真。通过静力学研究，系统在静态平衡位置可以获得准零刚度特性，而且通过对参数m和α的控制，在较小振动范围内扩大零刚度程度；通过动力学研究，研究了激励幅值、阻尼比不同参数改变对系统的力传递率、位移传递率的影响。适当增大激励幅值可以降低系统的起始隔振率，增大阻尼比可以降低系统的传递率。最后，通过实验验证在有、无负刚度机构的情况下系统的隔振效果。此系统在3～8 Hz的低频隔振方面有良好的性能，而且，根据文献显示，准零刚度隔振应用到康复机器人领域非常少，因此，本研究对机器人低频隔振方面具有创新性和理论指导意义。