多维路径与整体沟通——梯形面积公式推导

□何朝勇

【课前思考】

单元教学序列调整，使学生在探索三角形、平行四边形面积公式推导过程中积累了转化经验，充分感知并掌握了图形面积公式推导的两种策略——剪拼和倍拼。学生能根据图形转化前后的内在联系学会公式的推理表达。当学生具备这些知识基础与数学活动经验后，能否自主将其转化为推导梯形的面积计算公式呢？在推导过程中，学生可能会使用哪些转化策略，能否实现梯形面积公式的意义性建构？如何帮助学生沟通梯形、三角形、平行四边形之间的联系，进一步形成面积公式推导的整体方法意识？

一、激活经验，明确基本思路

学生在三角形、平行四边形面积公式推导过程中积累的经验和策略，为其自主推导“梯形面积公式”创造了条件。在教学中可通过对三角形、平行四边形面积公式推导过程的回顾（如图1），凸显图形之间的联系，点击图形转化的两种策略，激活学生已有的活动经验，明确推导“梯形面积公式”的基本思路为：转化图形—寻找联系—推导公式。

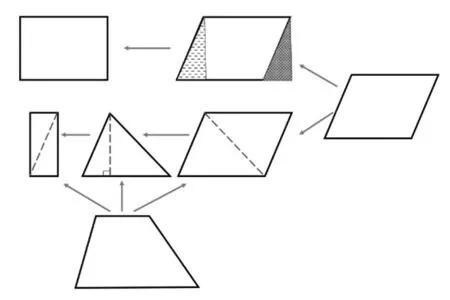
图1

二、操作交流，实现意义建构

梯形面积公式的意义性建构是本课教学的重点，也是教学的难点。教学中，教师可把梯形视为一个组合图形（如图2）来探索解决，为学生提供充分的探究材料（一个或多个梯形，告知四边及高的长度），鼓励学生用个性化思维探索梯形面积计算方法。呈现多种转化方法并非目的，更重要的是通过操作、交流、比较、概括等数学活动，归纳梯形面积计算的方法，实现梯形面积公式的意义建构。

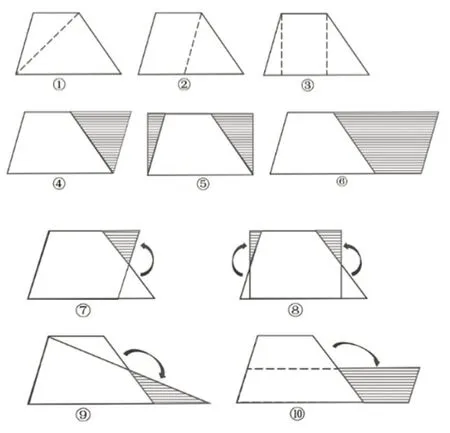
图2

三、沟通比较，形成方法意识

作为单元面积公式推导序列教学的最后一个公式，本课除了实现梯形面积公式的意义建构外，还有必要对梯形、平行四边形、三角形的面积计算公式进行整体沟通，通过三者间的变化关系（如图3），实现面积公式的整体架构。

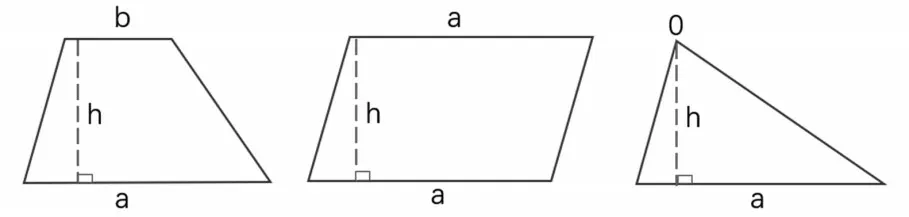
图3

通过沟通，力求让学生进一步形成面积公式推导的整体方法意识：推导图形面积计算公式时，都可以将新图形转化成旧图形，将未知转化成已知，进而解决新问题。

【教学实践】

一、回顾旧知，激活化归思想

师：我们已经研究了三角形、平行四边形的面积，还记得我们是怎么推导它们的面积公式的吗？

（学生回答略）

师：研究的思路都是把新图形转化成已经学过的有公式的旧图形，根据图形之间的联系推导出面积公式。今天我们来研究“梯形面积公式”，你打算怎么研究？

生：用剪拼、倍拼、分割等方法，转化成学过的图形。

二、自主探索，体验化归思想

师：请你尝试用某一种方法，把梯形转化成学过的图形，并计算它的面积。

（为每一位学生提供1 个梯形，已知上底3cm，下底7cm，高4cm）

学生独立探索或组内合作，教师巡视、搜集学生作品。

三、反馈交流，展示不同方法

学生使用的主要有三类方法：

（1）分割，求面积和。如图2中的①，列式：7×4÷2+3×4÷2=20cm2

（2）补拼（含倍拼），求面积差。如图2中的⑥，列式：7×4-4×4÷2=20cm2

（3）剪拼，等积变形。如图2中的⑨，列式：（7+3）×4÷2=20cm2

小结：方法不同，相应的算式也不同，但计算的结果是一致的。

四、方法比较，尝试表征公式

师：请仔细观察这些算式中，你有什么发现？

生：都用到了上底、下底、高这几个数据，和腰无关。

师：如果用字母a表示上底，b表示下底，h表示高，请你根据自己的转化方法，表示梯形面积计算公式。

学生独立表示梯形面积计算公式。

五、反馈交流，概括提炼公式

生：我觉得“S梯形=a×h÷2+b×h÷2”。

生：根据我的方法，应该这样求梯形面积，“S梯形=a×h+(b-a)×h÷2”。

生：我认为“S梯形=(a+b)×h÷2”。

师：方法不同，公式也不同，你们觉得哪个最简洁？

生：S梯形=(a+b)×h÷2。

师：其实，其他公式运用运算定律后也可以转化成“S梯形=(a+b)×h÷2”。比如“S梯形=a×h÷2+b×h÷2”，运用乘法分配律就可以转化成“S梯形=(a+b)×h÷2”，其他的方法也都可以，大家可以在课后尝试一下。

多媒体课件呈现三个梯形，讨论：这几个梯形是否也可以采用刚才的方法计算面积？

生：它们也可以用刚才的方法进行转化，都可以用“S梯形=(a+b)×h÷2”进行计算。

六、比较沟通，把握内在联系

（多媒体课件逐个呈现图4 中的图形，并让学生计算各自的面积。单位：cm）

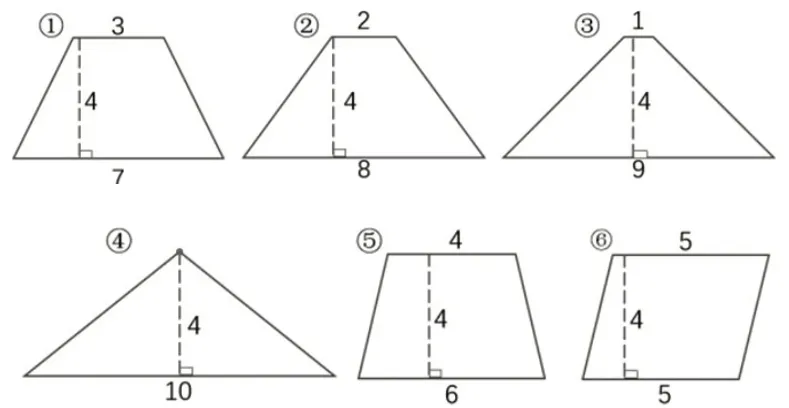
图4

出示①②两个梯形后，提问：想一想，下一个图形可能是怎样的？

生：上底1，下底9，高4。

师：继续变，下一个又会是怎样的图形？

生：上底是0，变成三角形了。

师：你会计算三角形的面积吗？

生：10×4÷2=20。

生：我们可以把三角形看作是上底为0的特殊

梯形，（0+10）×4÷2=20。

（出示⑤号图形）

师：你会求它的面积吗？

生：（4+6）×4÷2=20。

师：想一想，继续变化，会变成什么图形？怎样求它的面积？

生：会变成平行四边形，5×4=20（出示⑥号图形）。

生：也可以把平行四边形看作特殊的梯形，（5+5）×4÷2=20。

师：梯形的面积公式很厉害，用它还能求三角形、平行四边形的面积。

七、梳理总结，形成方法意识

师：这个单元我们研究了三角形、平行四边形、梯形的面积计算公式，在研究方法上有什么共同点？

生：都是把新图形转化成旧图形，根据它们之间的联系推导公式的。

师：把新知转化成旧知是一种非常重要的思想方法。如果今后遇到一种新图形或更加复杂的图形，你打算怎样求它的面积？

生：把新图形转化成学过的图形，根据联系推导公式，再运用公式求面积。

生：也可以用分割、剪拼、补拼等方法，求面积和或面积差。

【教学反思】

在面积公式推导新序列的课程中，学习的关键在于把梯形视为组合图形进行自主探究、沟通联系，实现面积公式的意义性建构。学生在此过程中进一步感受转化、极限、等积变形等数学思想方法，感知研究图形面积问题的一般路径。

一、顺延思路，悟思想方法

在之前的探究过程中，学生较好地积累了研究图形面积问题的基本方法和策略。本课通过对三角形、平行四边形面积公式推导过程的回顾，有效激活学生已有的知识基础和活动经验，顺延研究图形问题的思路，引导学生自主推导梯形面积公式。在我区两所学校的教学实践中，我们发现按照这一序列，95%以上的学生能把梯形视为一个组合图形，采用一种甚至多种策略进行“转化“，并能根据图形间的内在联系，实现梯形面积公式的个性化建构，统计如表1。

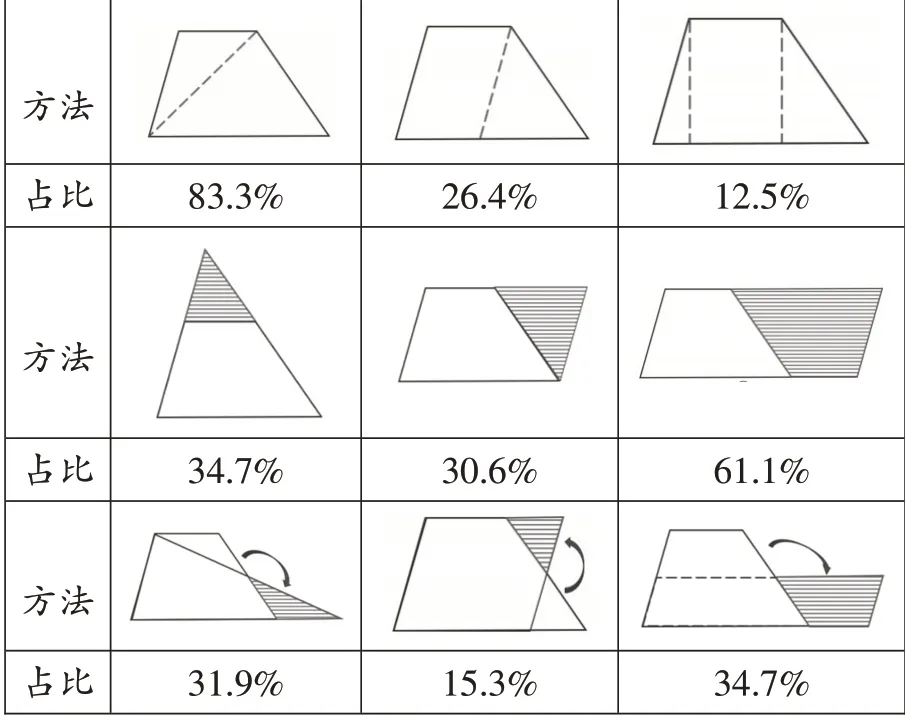
表1

从表1 可以看出，学生已初步形成“把新图形转化成旧图形”这一意识，并较好地掌握了剪拼、倍拼等转化方法。其中采用“把梯形分割成2个三角形”“2个梯形倍拼成平行四边形”这两种方法的人数较多，说明学生首选的转化目标就是三角形、平行四边形。采用剪拼法进行转化的比例看似不高，但实际上却是很多学生的首选方法，只不过有一部分学生因为不会找中位线而改变方法。更可喜的是，部分学生具备了策略调整意识，当他们发现在梯形上方拼补三角形，虽然实现了图形的转化，但却难以计算梯形面积时，他们会调整在右侧拼补三角形，把梯形转化成平行四边形。可见，学生能顺延研究三角形、平行四边形面积的思路探究梯形面积公式，更利于转化思想的落地。

二、多维路径，促意义建构

把梯形视为组合图形，让学生自主探究其面积公式的过程亦是开拓学生思维的过程。用不同的方法进行探究，不仅有助于提升学生的创新意识，还能发展学生的分析问题能力。我们选择1 个梯形作为材料，让学生尝试计算它的面积，学生的转化思路不同，相应的计算方法也不同。学生介绍个性化的方法，不仅是对自己探究成果的梳理，更开阔了他人的思维。

多维路径，看似给公式的提炼增加了难度，实则非常有必要。其一，学生能完成对梯形面积公式的个性化意义建构，远比“用一个冰冷的公式求面积”更具价值；其二，不同方法相同结果，虽然殊途同归，但解决问题过程的繁杂程度差异很大，这恰恰凸显了公式提炼的必要性。

三、整体沟通，强方法意识

将梯形和三角形、平行四边形的面积公式及研究方法进行整体沟通，有助于学生对公式的内化理解，进一步形成图形面积公式推导的方法意识。我们在教学中安排了两次沟通：首先，通过以题组练习的形式，对梯形、平行四边形、三角形的面积计算公式进行沟通，帮助学生感知三角形、平行四边形都可以看成特殊梯形的理念，打通三者之间的联系。其次，通过“在研究方法上有什么共同点？”“遇到一种新图形或更加复杂的图形，你打算怎样求它的面积？”这两个问题，帮助学生进一步形成整体方法意识，即探究不同图形的面积公式时，都可以将新图形转化成旧图形，将未知转化成已知。

教学中，将三者的面积公式进行沟通，有助于学生感知极限思想，可以使单元课之间有所呼应。同时，通过推导面积公式过程的沟通，有助于学生进一步感知研究图形面积问题的一般路径，为后续探索组合图形面积及圆面积公式做准备。