“面积公式推导”教学序列思考与实践

□宋煜阳

一、现象检视与思辨

基本平面图形面积，课程标准在第一、二学段分别给出了“探索并掌握长（正）方形的面积公式”“探索并掌握三角形、平行四边形和梯形的面积公式”“探索并掌握圆的面积公式”的教学目标要求。相应地，国内教材就平面图形面积公式的教学内容编排分为三个阶段：第一阶段为长方形面积公式，第二阶段为平行四边形、三角形和梯形面积公式，第三阶段为圆的面积公式。其中，第二阶段多数教材以“多边形面积”为单元，涵盖三种基本图形面积公式的推导和应用。这一单元的学习，是学生感悟“转化”等数学思想、积累数学基本活动经验、落实逻辑推理等学科核心素养的重要载体与关键阶段。

“多边形面积”单元编排，国内教材都采用了“平行四边形的面积—三角形的面积—梯形的面积”公式探索的序列，转化的基本活动经验路径为：先从平行四边形面积公式推导中形成转化思路，学会剪拼法（割补为长方形）；再从三角形面积公式推导中重点学会倍拼法（用两个全等的三角形拼成平行四边形）；最后重点运用倍拼法推导出梯形面积公式。实际教学表明，这种转化经验的学习路径存在以下缺陷：

推导方法单一，开放度不高。三种图形的面积公式推导，都只对剪拼法或倍拼法的其中一种方法展开主要探索，方法单一。即使部分教材在三角形面积公式推导中对剪拼法进行了补充介绍，也只是加以了解，侧重的依然是倍拼法。

暗示性强，学生自主探索空间不大。在进行平行四边形、三角形面积公式探索时，教师往往会提供或要求学生自备剪刀、两个一样的三角形等学具材料，带有很强的暗示性，削减了学生自主探索的空间。

转化方法之间切换跨度大，容易产生认知混乱。跨度之一是平行四边形转化为长方形，学生很难自发想到剪拼法，缺乏转化的心理准备和方法准备。跨度之二是三角形转化为平行四边形，学生很难自发从原有经验的剪拼法向倍拼法转身。

针对上述缺陷，也不乏相关课例就学习材料、学习路径改进的研究成果。笔者认为，本单元的面积公式推导，不能局限于单个课例的改进思考，需要基于转化经验的激活、形成、应用的序列视角对整个单元教学进行系统分析。

国内教材，一直是把“平行四边形的面积”作为单元的起始课和转化推导的种子课，甚至让我们形成了“必须先教学‘平行四边形的面积’才可以教学‘三角形的面积’”的思维定势。平行四边形虽然转化思路起点较低，但转化方法单一。而三角形面积公式推导要比平行四边形复杂得多，主要体现在富有较大的挑战空间和转化方法的多样性上。为此，要实现单元面积公式探索空间的进一步开放，理应把“三角形的面积”作为单元起始课和种子课，在第一时间同时激活、提炼剪拼法和倍拼法，为后续其他图形面积的转化做好方法准备。

那么，学生对三角形面积公式探索又有多少可行性呢？笔者选取了奉化区某城区小学五年级4个班150名学生，分两组进行了不同内容和要求的前测。

第一组前测对象为已经学完“平行四边形的面积”一课的72名学生，要求“限时10分钟，通过多种方法分别求出方格图中直角三角形、锐角三角形、钝角三角形的面积”。统计结果显示，直角三角形采用剪拼法占比88.9%、倍拼法占比48.6%，锐角三角形采用剪拼法（剪拼为长方形或平行四边形）占比36.1%、倍拼法占比6.9%，钝角三角形采用剪拼法和倍拼法均为0。数据一方面表明，在方格图支持下，近半数学生对直角三角形能够采用剪拼法、倍拼法两种方法进行探索；另一方面表明，学生对已有的经验方法不善于反思提炼和迁移运用，如倍拼法没能从直角三角形迁移到钝角三角形和锐角三角形。

第二组前测对象为没有学习“平行四边形的面积”一课的78 名学生，要求“限时3 分钟，通过多种方法求出方格图中直角三角形的面积”。统计结果为，采用剪拼法（剪拼为长方形）占比46.2%，采用倍拼法（倍拼为长方形）占比44.9%。这组数据表明，学生对直角三角形转化经验储备较为丰厚，在没有经历平行四边形面积公式推导的背景下，能对直角三角形面积自发产生较强的转化意识，自发呈现剪拼、倍拼两种转化方法。

从前测分析可以得出，单元面积公式推导先从三角形开始探索是可行的。考虑到学生转化经验差异和认知跨度，三角形的面积教学建议划分为“直角三角形的面积”和“一般三角形（锐角三角形和钝角三角形）的面积”两课时，前一课时重在激活经验、提炼方法，为一般三角形的面积探索提供思路与方法；后一课时重在经验积累、形成方法，为平行四边形、梯形面积探索提供方法应用与推广的支持。

需要补充说明的是，韩国教材和台湾地区教材，面积公式推导序列并非是从平行四边形开始的，而是先教学“三角形的面积”，再教学“平行四边形的面积”。这一事实依据也表明面积公式推导序列是动态的，完全可以基于学情进行单元整合，为公式推导提供更大的探索空间。

二、序列重组与定位

序列重组，是指基于整个单元，重新编排课时教学内容，构建单元面积公式推导教学新序列，优化学习路径，进一步提升面积公式探索的自主性与进阶性。重组后的单元教学序列，一方面强调转化经验的激活、积累与推广，另一方面强调转化方法的提炼、内化与应用。

笔者所在的研究团队，选取人教版教材进行了单元序列重组。“多边形面积”整个单元共编排了五个例题，其中前三个例题分别为平行四边形、三角形和梯形的面积，后两个例题是组合图形和不规则图形的面积。序列重组主要针对前三个例题（例1、例2、例3）与配套的三个练习（练习十九、练习二十、练习二十一）展开讨论，后两个例题及相关练习均保持不变。

教材序列（以下简称原序列），前三个例题与配套练习等教学内容一般安排六课时，其中新授、练习各为三课时。序列重组（以下简称新序列），保留“平行四边形的面积”“梯形的面积”课时内容，将原序列“三角形的面积”一课划分为“直角三角形的面积”和“一般三角形的面积”两课时，共计新授四课时、练习两课时，总课时数依然不变。原序列和新序列的具体课时内容对照如表1。

表1

新序列有两个基本要点：一是剪拼法和倍拼法并重、整体推进，将两种方法在本单元一以贯之；二是选用学生经验最为厚实的图形切入公式探索，降低转化方法的认知跨度，力求经验激发的自主性和方法形成的进阶性。

在这一思路下，剪拼法、倍拼法两种转化方法在学习路径上表现为“起于特殊，成于一般，应用于同类”，也即在直角三角形中激活经验、提炼方法，在一般三角形中积累经验、形成方法，在平行四边形和梯形中推广应用、整体沟通。

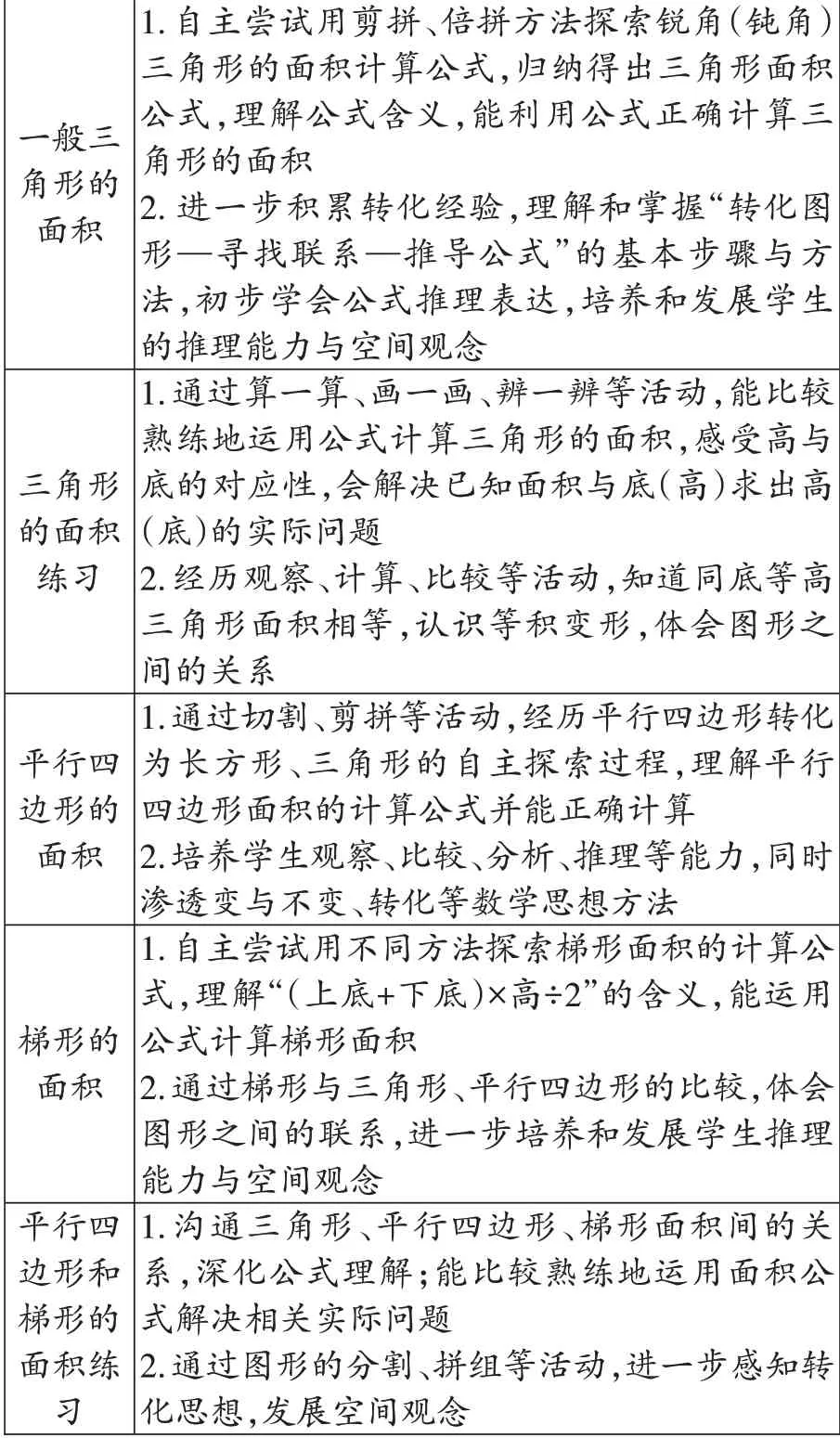
具体到新序列各个课例的目标定位，简述如下（表2）。需要指出的是，依然保留的“平行四边形的面积”“梯形的面积”与原序列相比，课时目标发生了一定变化。“平行四边形的面积”，除了剪拼法转化，还扩充了将平行四边形分割成两个三角形，以三角形面积公式为基础，通过“底×高÷2×2”推理得出平行四边形面积公式。“梯形的面积”，视作多边形面积问题解决，鼓励学生充分运用已有面积公式进行多种路径探索，并通过梯形、平行四边形、三角形图形之间的变化关系，沟通三者之间的联系，进一步形成面积公式推导的整体方法意识。

表2

续表

三、实验研究与启示

（一）实验基本情况

1.实验样本对象

宁波市奉化区两所城区小学，每所小学各选取五年级两个平行班，其中一个班为对照班，一个班为实验班。两所小学共有对照班两个，学生78 名（原来学业水平合格70名）；实验班两个，学生79名（原来学业水平合格73名）。本次实验只对原来学业水平合格学生的数据进行统计分析。

2.实验研究方法

以整个单元为研究周期，选派骨干教师分序列教学，对照班采用原序列，实验班采用新序列。整个单元教学结束后，对照班和实验班统一进行后测分析。针对不同学业水平等级的学生群体差异，研究中把对照班、实验班的学生划分为合格、良好、优秀三个等级，其中合格人数占比15%，良好人数占比40%，优秀人数占比45%。

3.测查内容说明

面积公式推导认知水平测查，分为公式应用、公式推导再现、新图形面积探究三个维度。公式应用，侧重考查面积公式程序运作、公式变式记忆和底高对应记忆水平；公式推导再现，侧重考查基本图形公式含义理解、公式推导说理水平；新图形面积探究，侧重考查新图形转化方法的类比迁移水平。

（二）实验结论与启示

1.实验班在公式推导再现维度占据优势，反映新序列学习转化的基本活动经验更为厚实，推理能力得到明显提升

测查数据显示，对照班和实验班在公式应用维度没有明显差异，但在公式推导再现维度实验班存在较大优势。

测查题中提供了底6 高4 的三角形，要求学生画出“6×4”表示的图形，并给出这个三角形剪拼法转化的示意图（图1），要求学生写出推导过程。学生推导能力水平划分为四个层级：水平0，错误或没作答；水平1，只提到将三角形转化为长方形；水平2，说明三角形的底和长方形的长相等，三角形的高的一半和长方形的宽相等；水平3，完整表达推导说理过程（图2为学生作品）。

图1

图2

实验班优势一，三角形转化的路径更为多元。画出“6×4”表示的图形，反映的是对三角形倍拼后图形种类的认知。对照班转化为平行四边形占比95.4%，长方形占比4.6%；实验班转化为平行四边形占比62.5%，长方形占比37.5%。实验班对转化的两种图形选择更为均衡。实验班优势二，三角形剪拼转化的公式推导说理能力水平更高。推导能力水平3，对照班占比30.0%，实验班占比57.5%，实验班优势明显，近60%的学生表现了较强的逻辑推理能力。

这两处优势，都证实了新序列在公式推导的含义理解、转化路径和说理水平方面有更为充分而深刻的体验，学习路径得到优化。

2.实验班在新图形面积探究维度存在优势，反映新序列学习发挥了经验迁移的作用，特别是对低起点的学生产生较为明显的影响

新图形面积探究维度，安排了圆的面积公式推导，要求学生画一画、写一写转化和推导的想法。探究能力水平划分为四个层级：水平0，错误或没作答；水平1，只提到转化为已学图形，没有转化说明或图示；水平2，给出圆和正方形或三角形进行转化的图示，没有转化说明或说明不清晰；水平3，给出把圆分割成多个三角形转化的图示，并有初步推导思路。对照班和实验班的整体数据如表3，不同学业水平等级的群体数据如表4。

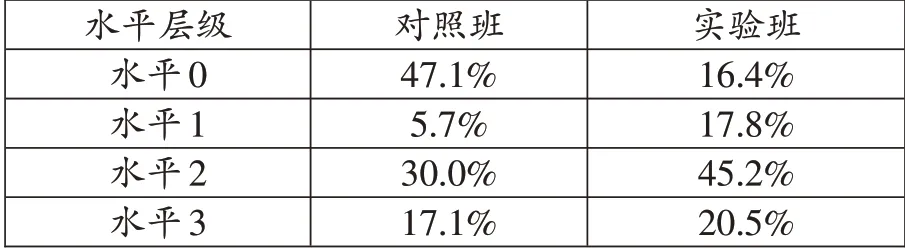
表3

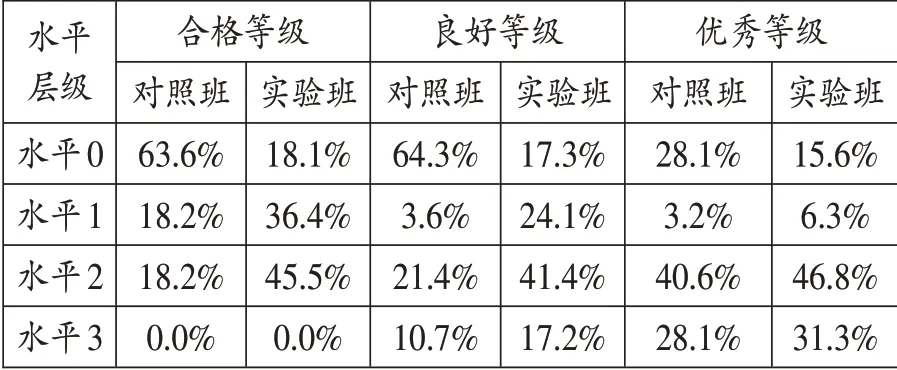
表4

表3 显示，实验班在整体上要略优于对照班，在水平0的占比上优势较为明显。从表4可以看出，三个等级学生在水平3上占比基本持平；学业水平合格、良好等级的实验班学生，在水平0～水平2 之间有较大幅度提升。分析可知，对于学业水平起点较低的学生，新序列的学习更有利于增强转化意识，更有利于面积公式推导方法的形成与类比迁移。