水平运动模拟器复演随机海浪谱实验*

薛米安， 邢建建， 苑晓丽， 陈奕超， 罗铆钧

(1.河海大学海岸灾害及防护教育部重点实验室 南京,210098) (2.河海大学港口海岸与近海工程学院 南京,210098) (3.河海大学理学院 南京,210098)

引 言

海洋工程结构物如浮式生产储卸油系统(floating production storage and offloading，简称FPSO)、半潜式平台、大型液货船等主力海洋工程装备，长期遭受着风浪流等复杂动载荷的作用，尤其是在波浪作用下常常会引起上述结构物的剧烈运动。海洋波浪引发海洋结构物产生的运动属于随机运动。受造波港池模拟随机波浪能力的限制，实验中难以准确描述浮式结构物在复杂波浪场中的动态响应，给研究带来了诸多不便。由于海洋波浪的准确复演是海洋工程模型实验保证试验结果可靠性的重要因素，因此除建造精准的大型波浪水池外，随机运动模拟器成为复演极端波浪、地震等各种海洋环境的重要途径。

皮阳军等[1]认为随机运动模拟器在装备研发和可靠性验证中具有举足轻重的作用，因此科研人员对各种类型的模拟器性能开展了卓有成效的研究。武伟等[2]设计了一套能够提供典型海浪运动模拟的电液式振动台。于大泳等[3]运用蒙特卡洛研究了对接机构运动模拟器并对其位姿精度进行了概率分析。张元等[4]设计并测试了一种新型的六自由度运动模拟器。梁凯等[5]基于动态性能仿真测试分析了六自由度运动模拟器的各项性能指标。吴博等[6]研究了液控运动模拟控制系统并分析了六自由度运动模拟器的静态及动态性能。凌明祥等[7]研究了液压振动台的非线性摩擦力与参数辨识技术，为振动台加速度波形失真补偿提供了参考。Airouche等[8]研究了六自由度振动台谐波信号再生的高保真问题。然而上述研究鲜有提及运动模拟器对随机海浪谱的复演精度问题，同时海浪谱类型及主要参数对精度的影响也较少报道。但是这些因素对运动模拟器在海洋工程模型试验中的应用极其重要，直接关系着实验结论的精度，尤其是对于随机波浪激励下的液体晃荡问题[9-10]，因此亟需开展各种海浪谱生成随机运动位移的试验。

实际海域中的海浪变化十分复杂，对于充分成长的海浪，可以被认为是一个平稳的随机过程。随机海浪也被称为不规则波。对不规则波的产生方法，Ketabdari等[11]认为可以通过有限数量正弦单色波的叠加、风生波时间序列的原型观测等方法获得。尽管不规则波是由具有不同频率和相位余弦或正弦函数叠加而成，但是不同海域的波浪特性不同，因此每种谱生成的不规则波仍具有自己的特性。在该研究中以JONSWAP谱(简称J谱)和Bretschneider谱(简称B谱)分别作为输入设计谱驱动平台按照指定的随机波谱作不规则运动，通过改变谱峰周期和有效波高分析不同参数下该模拟平台实际运动位移的能谱曲线与理论谱的差异性，并讨论两种设计谱所产生随机运动位移的主要统计特征。

1 海浪谱及其生成的随机运动位移

1.1 两种海浪谱表达式

J谱的表达式[12]为

其中：Hs和Ts分别为有效波高和周期；Tp和fp分别为谱峰周期和频率；γ=3.3为谱峰增强因子。

B谱的表达式为

(5)

其中：Hs为有效波高；ωp为谱峰频率。

该谱由Bretschneider在1959年通过无因次波高和无因次波长的联合分布函数导出的二参数谱，它适用于成长阶段或充分成长的风浪。该谱是以外部观测的各种频率的波浪所贡献的能量代替各组成波提供的能量，所给出的谱实质上是波能在各种外观波长之间的分布。公式中的频率有的使用圆频率ω(rad/s)表示，有的使用频率f(Hz)表示，为了使得谱密度函数S(ω)与S(f)之间能够相互转换，给出了如下的转换关系

S(f)=2πS(2πf)=2πS(ω)

(6)

1.2 随机运动位移生成原理

不规则波由有限数个不同波幅、频率和相位的正弦波线性叠加而成，其波面表达式为

(7)

其中：ωi为第i个线性波的频率；N为线性波的个数；ai和φi为每个线性波的波幅和相位。

相位φi为0～2π范围内的随机变量，波幅的表达式为

(8)

其中：Δω为频率间隔。

根据线性造波理论，运动模拟器的水平运动速度可以表示为

(9)

其中：Ki为转换函数。

其表达式为

(10)

和不规则谱波面的表达式类似，由海浪谱生成的随机运动方程可写为

(11)

其中：x(t)代表可产生一个随机的水平运动；ai和ωi分别为每一个简谐波的振幅和频率；φi为0～2π范围内的随机变量。

在试验中，当需要产生一个随机位移时，首先根据海浪理论谱，利用傅里叶变换将其展开成一个电压时间序列值控制信号，此信号经运动控制卡转换成运动方向和速度两路数字控制信号送给伺服控制驱动器，驱动伺服电机做往复运动，从而带动水平模拟器做相应的随机运动。

1.3 测量仪器及试验工况

平台运动的实际位移由位移传感器实时测量。如图1所示，位移传感器一端固定在试验平台上，另一端与固定在地基上的结构物相连。试验中采用的位移传感器量程为0～50 cm，精度为±0.5%F·S，采样频率为100 Hz，通讯接口为USB型，可以直接连接在计算机上并通过基于Visual Studio软件平台开发的SDA1000型数据采集软件实时显示并保存位移数据。

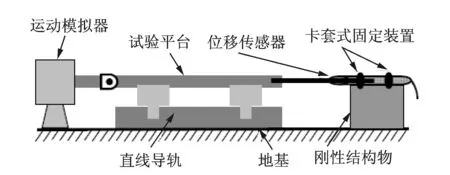
图1 运动模拟装置中的位移传感器布置示意图Fig.1 Layout of displacement sensor in movement simulator

表1列出了两种设计谱的9组有效波高和谱峰周期， 用于研究不同参数条件下海浪谱生成的随机位移的统计特征。由谱密度函数可知，波浪谱的有效波高和周期给定后即可确定谱形。通过改变有效波高和周期，可改变谱形进而通过运动模拟器生成不同的随机运动位移。

表1 B谱和J谱的9组有效波高H及周期T

2 随机运动位移及相应的频谱密度

图2为不同谱峰周期和有效波高条件下两种海

浪谱B谱和J谱分别生成的实际水平随机运动位移。由图2可知，在相同的有效波高和谱峰周期条件下两种海浪谱所产生的随机运动位移没有显著的差别，并发现由两种能谱产生的不规则运动位移的极值也没有显著的变化。当有效波高固定不变时，由图2(a)～(c)及图2(A)～(C)可知两种实测海浪谱所生成的不规则运动位移的极值并不随着谱峰周期的增大而显著的增大或减小。当谱峰周期保持不变时，由图2(c)～(e)和图2(C)～(E)可知两种实测海浪谱所生成的不规则运动位移的极值均随着有效波高的增加而显著增大。

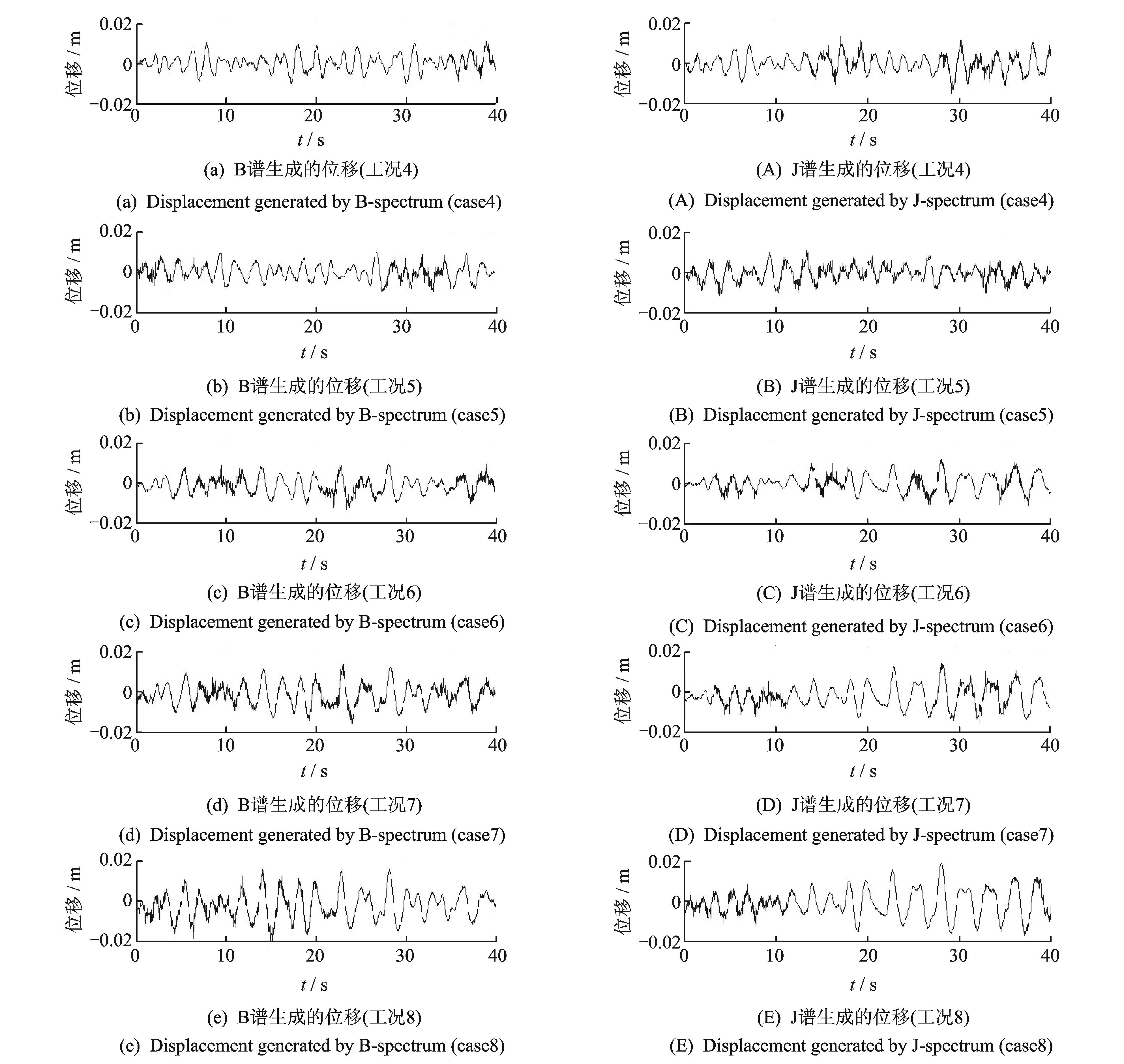
图2 不同谱峰周期和有效波高条件下海浪谱生成的实际平台运动位移Fig.2 The movement displacement generated by B-spectrum and J-spectrum with different period and significant wave height

为了进一步分析随机位移的频谱变化，图3给出了与图2相应的不同谱峰周期和有效波高条件下海浪谱生成的实际平台运动位移的实测频谱密度与理论频谱密度的比较关系。从图3中可以看出，当两种海浪谱具有相同的有效波高和谱峰周期时，其谱形存在较大的差异，B谱较平缓属于宽带频谱，J谱较尖锐属于窄带频谱。因此J谱的波浪能量在频域上的分布也较B谱集中。当有效波高固定不变时，由图3(a) ～ (c)及图3(A)～(C)可知随着谱峰周期的增大两种海浪谱的谱峰频率均由高频向低频推移，实测频谱密度的最大值也随着谱峰周期的增大而缓慢增加。当谱峰周期保持不变时，由图3(c)～(e)和图3(C)～(E)也可知两种实测海浪谱的频谱密度最大值随着有效波高的增加而显著增大。此外，从图3中还可以看出随着谱峰周期的增加实测频谱密度越来越偏离理论值，也就是低频运动越来越难被精确模拟，尤其是对于能量在频域上相对集中的J谱。

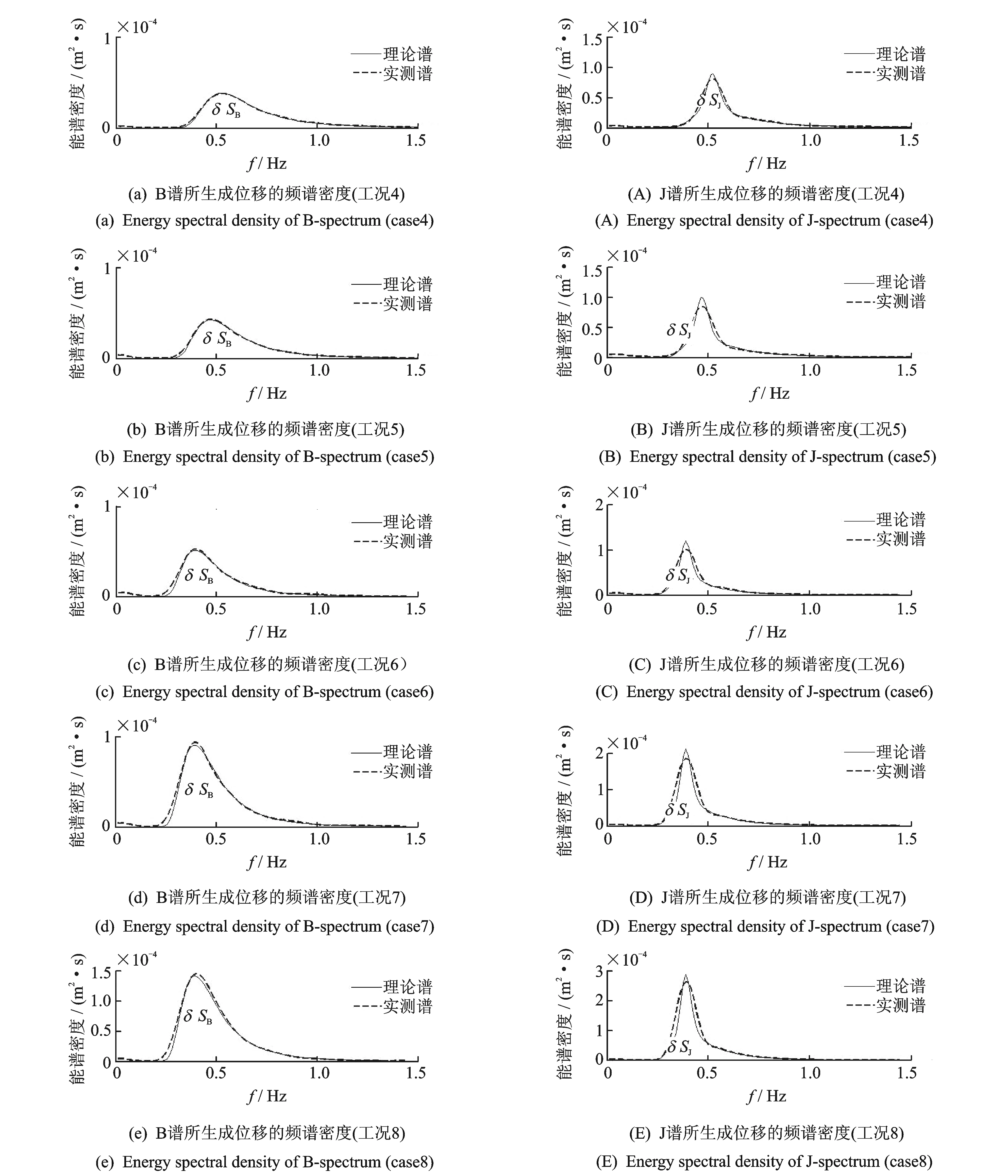
图3 不同谱峰周期和有效波高条件下海浪谱生成的实际平台运动位移的实测频谱密度与理论频谱密度的比较Fig.3 Comparison of theoretical spectrum and measured spectrum of displacement generated by B-spectrum and J-spectrum with different period and significant wave height

3 随机运动位移及其快速傅里叶变换结果的统计特征分析

通过对水平随机运动位移极值的统计分析可以确定谱峰周期T及有效波高H对水平运动模拟器冲程d的影响规律。图4给出了两种海浪谱所生成随机运动位移的最大值dmax、最小值dmin随谱峰周期T及有效波高H的变化关系。从图4(a)中可以看出当有效波高H为0.015 m保持不变时，除由B谱生成水平随机运动位移的最大值随着谱峰周期的增加而减小外，B谱所生成水平随机运动位移的最小值和J谱生成的水平随机运动位移的最大值及最小值均不随谱峰周期的增加而单调增加或减小。同时从图4(a)中可以观测到，除图2(B)(工况2)中出现的由J谱所生成的一个较大的随机运动位移外，由两种海浪谱所生成水平随机运动位移的最大值与最小值之间并没有显著的差异。当谱峰周期为2.4 s保持不变时，从图2(f)～(i)和(F)～(I)以及图4(b)中可以看出两种海浪谱生成的随机运动位移的最大值随着有效波高的增加而增加；同一有效波高时两种海浪谱所生成随机运动位移的最大值与最小值没有显著差异。

图4 两种海浪谱所生成随机运动位移的最大值、最小值随谱峰周期T及有效波高H的变化Fig.4 The maximum/minimum value of displacement generated by B-spectrum and J-spectrum with different period T and significant wave height H

标准差也被称为标准偏差，反映了一组数据的离散程度。从图5(a)中可以看出随着谱峰周期T的增加，J谱所生成水平随机运动位移的标准差σJ均大于由B谱生成水平随机运动位移的标准差σB，表明J谱生成的随机位移数据集具有较大的离散度，主要原因是J谱比B谱的能量在频域上的分布较集中。此外，从图5(a)中也可以发现两种海浪谱所生成随机运动位移数据的标准差并不随谱峰周期的增加而单调的增加或减小。当周期等于1.5 s时两种海浪谱生成的随机运动位移都具有最大的标准差，即位移数据具有较高的离散度。从图5(b)中可以看出，两种海浪谱所生成随机运动位移的标准差也随着有效波高的增大而增大；同时由J谱生成的随机运动位移的标准差均大于由B谱所生成随机运动位移的标准差，表明两种海浪谱生成的随机运动位移数据的离散程度也随着有效波高的增大而增大，且J谱所生成随机运动位移数据的离散程度大于B谱所生成随机运动位移数据的离散程度。

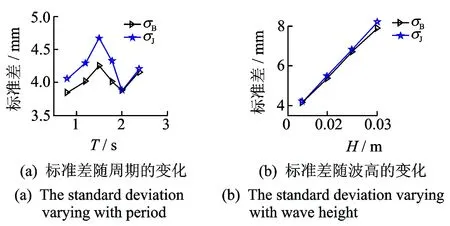
图5 两种海浪谱所生成随机运动位移的标准差随谱峰周期T及有效波高H的变化关系Fig.5 The standard deviation of displacement generated by B-spectrum and J-spectrum with different period T and significant wave height H

实测频谱密度与理论谱之间的拟合优度R2反映了模拟器复演随机运动的精度。图6(a) 显示除工况2外B 谱实测谱与理论谱之间的拟合优度均大于J谱实测谱与理论谱间的拟合优度并且随着谱峰周期的增加J谱实测谱与理论谱间的拟合优度逐渐减小，这是由于随着谱峰周期的增加J谱的谱型越来越尖锐， 能量也越来越集中在峰值频率上。上述分析表明，该水平运动模拟器能够较精确地复演宽频带的B谱，拟合优度R2可以达到0.99以上，而对具有较大谱峰周期的窄频带J谱所生成的随机运动位移并不能较精确地复演且R2随着谱峰周期的增大而减小，表明谱峰周期是影响窄频带J谱复演精度的主要因素。当谱峰周期不变时，随着有效波高的增大，图6(b)显示B谱的拟合优度均大于J谱的拟合优度，主要原因如图3所示。和J谱相比，B谱是一种宽频带谱，能量在频率上的分布相对分散，所生成随机运动位移的离散程度较小，数据较稳定，因此水平模拟器能够较准确地复演由B谱生成的随机运动。此外，由图6(b)也可发现随着有效波高的增加，两种海浪谱实测谱与理论谱的拟合优度基本上保持不变，J谱型的拟合优度在0.975左右，B谱型的拟合优度约为0.995。

图6 两种海浪谱的实测频谱与理论谱的拟合优度R2随谱峰周期T及有效波高H的变化关系Fig.6 The determinate coefficient R2 between theoretical spectrum and measured spectrum of displacement generated by B-spectrum and J-spectrum with different period T and significant wave height H

频谱密度对频率的积分可以给出信号的方差，同时也反映了信号能量的大小。对图3中9组实测频谱密度曲线在频域上进行积分可获得频谱密度的方差，即实测频谱密度曲线与频率轴之间的面积δS，该值不仅反映了实测谱数据的离散程度也一定程度上反映了能量的大小。从图7 (a) 中可以看出J谱实测频谱密度对频率的积分δSJ在有效波高为0.015 m、谱峰周期0.8～2.4 s范围内均大于B谱实测频谱密度对频率的积分δSB，表明J谱频谱密度的离散程度及在频域上的总能量均大于B谱频谱密度的离散程度和在频域上的总能量。从图7(b)中可以观测到，频谱密度函数对频率的积分面积即实测谱型的方差也随着有效波高的增加而增加且J谱实测谱的方差大于B谱实测谱的方差，和图5(b)得出的结论一致，表明J谱相对B谱而言是一种高离散度的谱型，同时离散程度随着有效波高的增加而增加。

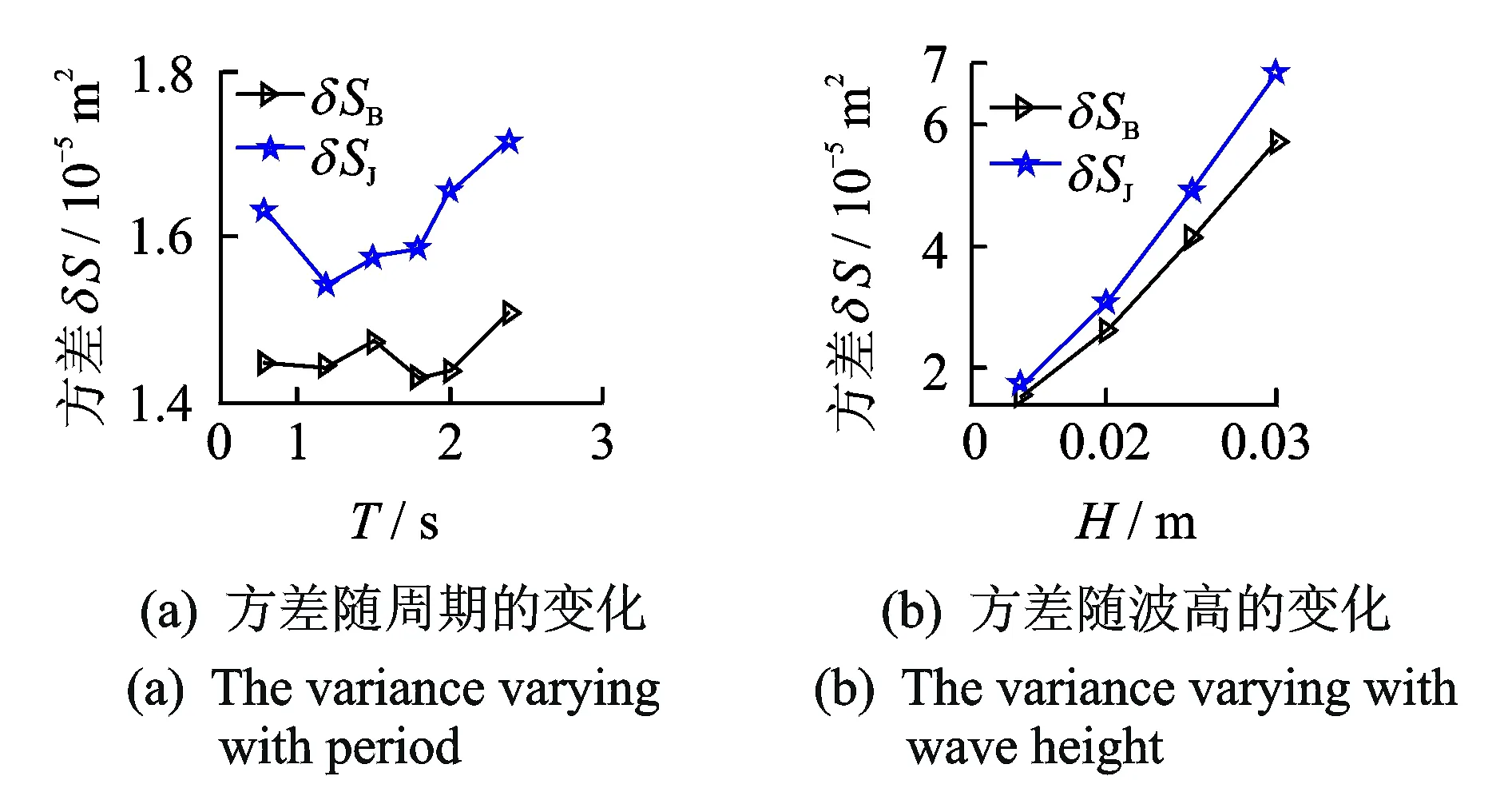
图7 两种海浪谱的实测频谱密度对频率的积分面积即方差δS随谱峰周期T及有效波高H的变化Fig.7 The variance of measured spectrum of displacement generated by Bretschneider spectrum and JONSWAP spectrum with different period T and significant wave height H

4 结束语

选择典型的宽频带B谱和窄频带J谱，通过实验研究了水平运动模拟器模拟这两种海浪谱型所生成随机运动位移的主要统计特征、复演精度以及谱峰周期和有效波高对生成的随机运动位移的主要统计参数的影响规律。得出如下结论：a.B谱相比J谱是一种具有较高离散程度的谱型；b.水平运动模拟器对B谱的复演精度大于对J谱的复演精度，且谱峰周期是影响J谱复演精度的主要因素；c.有效波高保持不变时，两种海浪谱生成的随机运动位移的统计值并不随着谱峰周期的增加而单调的增加或减少；d.谱峰周期保持不变时，两种海浪谱生成的随机运动位移的最大值、标准差及实测频谱密度函数的方差均随着有效波高的增大而单调的增大。

本研究一方面直接给出了该类型运动模拟器精确模拟不同类型谱的能力；另一方面也为在实验室内界定该类型随机运动模拟器精确模拟窄频带J谱的周期范围提供了方法借鉴，最终为合理利用该实验装置准确模拟不同的运动环境提供了科学参考依据。该实验装置可被广泛应用于简谐或随机波浪激励下液舱或储液罐内的液体晃荡问题研究，获取液舱或储液罐内的压力分布规律，为优化设计液货舱结构提供科学实验数据[13-14]。