基于包络加窗同步平均的行星齿轮箱特征提取*
2019-05-09赵磊,郭瑜,伍星
赵 磊, 郭 瑜, 伍 星
(昆明理工大学机电工程学院 昆明,650500)
引 言
行星齿轮箱广泛应用于风力发电、直升机、工程机械等现代大型复杂机械装备中[1],恶劣的工作环境导致其运行工况复杂,转速和负荷等工况参数的变化将导致其振动信号具有明显的非平稳性[2],不直接满足傅里叶变换的平稳性要求[3]。另一方面,在行星齿轮箱故障诊断中,以传感器安装在固定齿圈上方的行星传动为例,一个或多个行星轮同时与齿圈和太阳轮啮合,并随行星架围绕太阳轮旋转,同时绕其自身轴线自转,其振动为多振源耦合振动,且振动传递路径具有时变性,导致其振动频谱结构非常复杂[4]。如何有效提取行星齿轮箱局部故障特征是目前故障诊断学科研究的重点领域之一。
包络分析是常用的振动信号幅值解调分析方法,适用于轴承、齿轮等故障弱特征提取[5-6]。因此,应用包络分析提取行星齿轮箱故障值得深入研究。在现有包络提取方法中,Antoni[7]提出的基于谱峭度(spectral kurtosis,简称SK)的包络提取,能自适应获取优化的共振解调频带,有效提取齿轮、轴承的早期故障特征。但对行星齿轮箱振动而言,由于多振源耦合、振动的时变传递路径等问题,仅仅分析包络信号,依然很难提取出故障特征频率成分信息。
同步平均是从混有噪声的复杂周期信号中提取感兴趣周期分量的常用方法[8-9],可针对时域或角域信号,对于存在转速波动的非平稳信号,角域同步平均可取得较好的效果。同步平均实现上是将信号分段,再根据时标信号对齐相位进行叠加后平均,但对于行星齿轮箱振动信号,由于时变传递路径的影响,很难对齐相位,因此无法直接应用同步平均。
为解决行星齿轮箱振动的时变传递路径问题,McFadden[9-10]提出一种加窗同步平均法。Samuel等[11]对其进行了改进,降低了振动时变传递路径对振动分析的影响。笔者结合包络提取、计算阶比跟踪(computed order tracking,简称COT)和加窗同步平均的优点,提出一种能有效提取早期故障特征、避免转速波动及振动时变传递路径影响的基于包络信号角域加窗同步平均的行星齿轮箱故障特征提取法,并通过试验验证了该方法的有效性。
1 理论基础
谱峭度可以用来描述特定频带内振动冲击成分的强弱[13]。采用基于解析滤波器的Fast Kurtogram[7]算法,其具体实现是通过构建一系列不同频带的滤波器组计算各频带的谱峭度值,选取谱峭度最大的滤波器中心频率及其滤波带宽作为包络提取中共振解调的中心频率和滤波带宽[6]。通过高频共振解调包络提取可以避免频带外的低频强干扰,适合于轴承、齿轮早期故障特征提取[6-7,12]。
COT[3]是针对旋转机械非平稳工况下的一种避免频谱分析产生频率模糊现象的技术,通过对振动信号进行等角度重采样将其转换为角域准平稳信号,满足傅里叶变换对信号的平稳性要求,因此采用阶比分析对于非平稳工况更有优势。首先通过对振动信号和转速脉冲信号进行同步采样,再通过转速脉冲信号作为键相时标,对振动信号进行等角度间隔重采样转换为准平稳信号,对所得的准平稳信号进行频谱分析得到阶比谱[3,6,13-14]。
同步平均(synchronous averaging,简称SA)主要包括时域同步平均(time synchronous averaging,简称TSA)和角域同步平均(也称旋转域平均)(rotation domain averageing,简称RDA)[13],通过SA可以消除与给定频率无关的信号分量(包括噪声和无关的周期信号),提取与给定频率有关的周期信号,提高信号的信噪比[8],其实现可解释为通过对振动信号和转速脉冲同步采样,以转速脉冲为参考相位对振动信号分段截取,再对截取信号进行叠加平均。对存在转速波动的变工况非平稳信号,可用COT技术将时域振动信号转换为角域,再进行角域同步平均[6]。但对于行星齿轮箱振动信号由于时变传递路径的影响,传统同步平均并不能直接应用。
2 行星齿轮箱包络信号角域加窗振动分离
2.1 传递路径对振动测试信号的影响
以传感器安装在固定齿圈上方的行星齿轮箱为例,由于行星轮的自转和公转,行星齿轮箱振动存在时变传递路径问题。
行星齿轮箱齿轮啮合振动有多条路径传递到传感器,考虑最短传递路径振动衰减较小,对行星轮齿(包括故障齿与非故障齿)与距离安装在箱体顶端传感器最近位置齿圈齿啮合振动进行分离,太阳轮齿与行星轮啮合产生振动则是通过行星轮传递到齿圈上传感器[4],如图1所示。
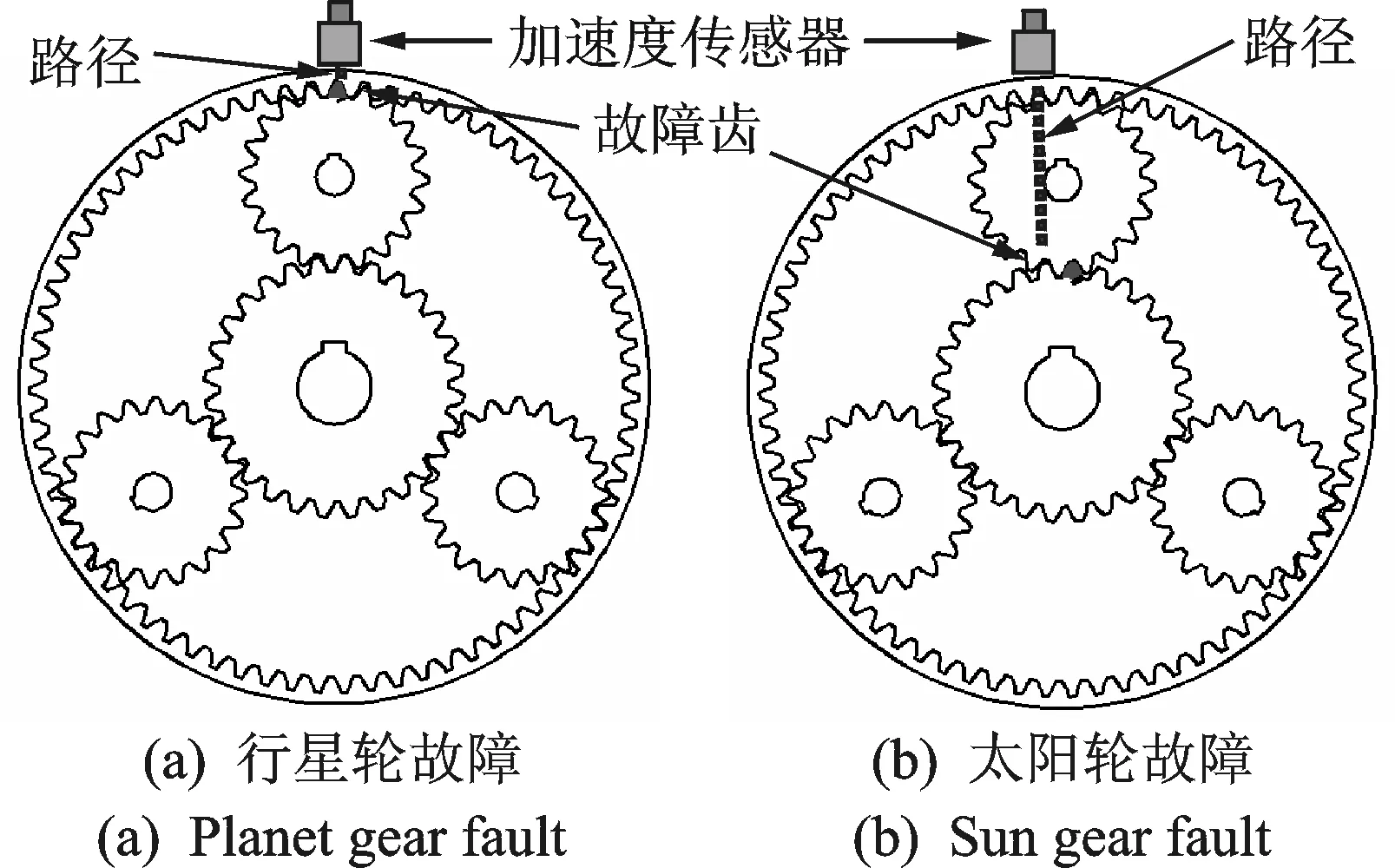
图1 故障传递路径Fig.1 Sun gear fault paths
2.2 基于角域加窗振动分离信号构建
根据行星轮系的的传递特性,当行星架旋转过一定圈数后,行星轮上次与齿圈上固定齿啮合的齿会再次重复啮合,太阳轮则是通过行星轮传递到齿圈[4],依据行星齿轮箱的这种传递特性,可对行星轮或太阳轮信号进行振动分离。对重复啮合的最小圈数定义[11]为
nR,g=LCM(Ng,Nr)/Nr
(1)
其中:LCM表示求最小公倍数;Nr,Ng分别为齿圈齿数和故障齿轮齿数;g表示行星轮或太阳轮。
对行星齿轮箱各个齿轮进行编号,固定齿圈上齿啮合齿号pn,g可以根据式(2)[11]求得
Pn,g=mod(nNr,Ng)+1
(2)
其中:mod为求余;n为行星架旋转圈数。
依据行星齿轮箱的这种传递特性,对行星架每旋转一圈对包络信号重采样的角域信号进行加窗截取,根据文献[11]对窗函数及窗宽的研究论述,本研究选用Tukey窗,包络角域信号加窗则可以根据等角度窗宽加窗。研究表明,窗宽选取5齿宽可取得较好结果,因此笔者选取5齿宽。加窗振动分离信号合成过程如图2所示,360°为行星架旋转一周。
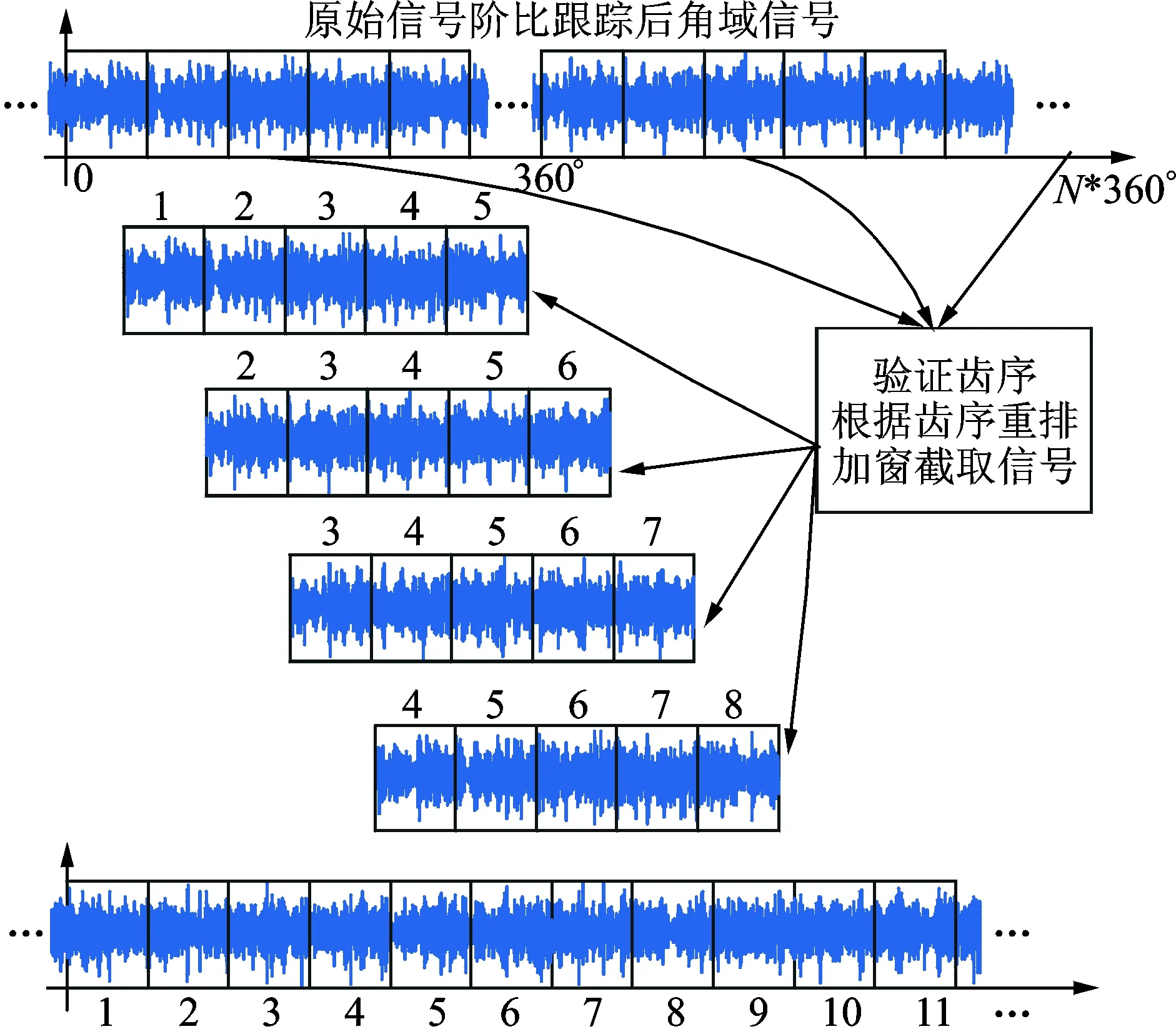
图2 基于角域加窗振动分离信号合成过程Fig.2 The synthesis process based on separation vibration signal with windows function in angle domain
角域加窗信号依然为角域信号,根据式(2)求取的啮合齿序特征,按照齿号顺序对目标齿轮信号进行重构,保证同一个齿的振动信号在同一个位置进行叠加重构,最终得到原始顺序齿号的目标齿轮振动信号。
2.3 故障特征分析
包络分析是提取早期故障特征的有效方法,但对于行星齿轮箱,由于振动时变传递路径影响,需先对包络信号进行角域加窗振动分离,才能得到故障的特征阶次,并进一步对故障进行诊断。
阶次分析中选用行星架转速脉冲信号作为参考信号,根据行星齿轮的传动特点,啮合频率[11]为
fm=Nrfc=Np(fp+fc)=Ns(fs-fc)
(3)
则相对于行星架的啮合阶次为
(4)
行星轮故障频率为行星轮相对于行星架的转频[11]为
(5)
则行星轮的故障阶次为
(6)
太阳轮故障频率为太阳轮相对于行星架的转频[11]为
(7)
则太阳轮的故障阶次为
(8)
其中:Nr,Np,Ns分别为齿圈、行星轮、太阳轮的齿数;fm为齿轮箱啮合频率;fc为行星架旋转频率;fp为行星轮的绝对旋转频率;fs太阳轮的绝对旋转频率。
3 基于包络角域加窗的振动分离信号同步平均
结合包络弱特征提取、角域信号避免转速波动、振动分离消除时变传递路径影响和同步平均提高信噪比的优势,提出基于包络角域加窗同步平均的行星齿轮箱振动分离信号特征提取方法,如图3所示。基本步骤包括:a.对行星齿轮箱振动信号进行基于谱峭度的包络提取;b.利用阶比跟踪技术对包络信号虚实部进行角域重采样,得到准平稳信号;c.对包络虚实部角域信号分别进行振动分离,对角域信号等角度加窗截取,根据齿轮齿序啮合特征重构分离信号;d.分别对虚实部振动分离信号进行同步平均,对虚实部平均后的信号构造振动分离信号;e.频谱分析得到阶比谱,实现行星齿轮箱故障特征提取。
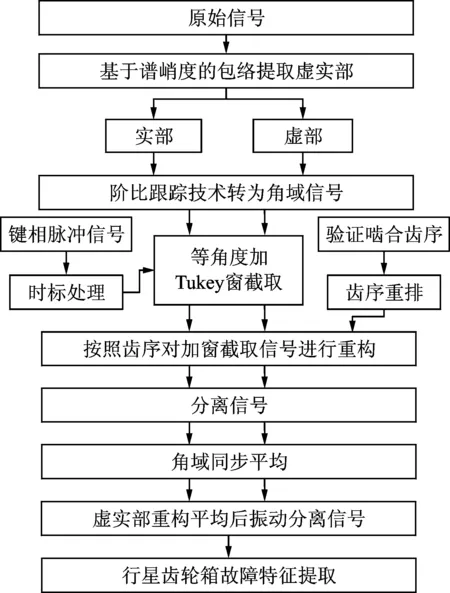
图3 基于包络角域加窗的振动分离信号同步平均过程Fig.3 Process of vibration separation signal synchronous average based on angle domain windowed of envelope signal
与传统的时域加窗同步平均法[9]相比,文中所提方法具有以下优势:a.通过将时域信号转为角域信号,每圈重采样点数可设置为齿数的整数倍,再通过固定齿宽进行加窗,相对于传统的时域加窗提高了加窗截取的精度;b.针对行星齿轮箱中故障特征相对较弱的特点,结合包络解调对解调频带外强干扰抑制,而对进入解调(共振)区故障对应的弱冲击特征进行放大的优势,对包络信号进行加窗提取,实现对弱故障特征的提取。
4 实验信号分析
4.1 实验说明
实验研究对象为NGW型行星齿轮传动故障诊断综合实验台,其由电机、行星齿轮减速器及负载组成。选择单级行星齿轮箱(2K-H行星传动)进行数据采集,如图4所示。

1-电机;2-电涡流传感器;3,4,5-加速度传感器图4 行星齿轮传动实验台Fig.4 Test rig of planetary gearbox transmission
齿轮箱参数如表1所示。分别采集正常状态振动信号,模拟行星轮故障信号和模拟太阳轮故障信号,为模拟行星齿轮箱局部故障,对一行星轮轮齿加工一条约4 mm的齿根裂纹故障,对太阳轮轮齿加工一约3.7 mm的齿根裂纹故障,如图5,6所示。试验中在行星齿轮箱上安装了3个加速度传感器采集振动信号,具体布置如图4中3,4,5处,采样频率为51.2 kHz,最终分析信号选取安装在齿圈上方箱体上的加速度传感器采集的信号,加速度传感器型号为DH112,灵敏度为5.20 pC/g;电荷放大器放大倍数为30 mV/pC;在连接太阳轮的输入轴处安装了DH904电涡流传感器,灵敏度为2.5 V/mm,用于获取输入轴转速脉冲;实际转速根据转速脉冲计算,约为1 000 r/min。行星轮与齿圈、行星轮与太阳轮设计齿轮副中心距及极限偏差为56.5±0.035 mm。

表1 行星齿轮箱参数
首先对包络信号重采样得到的角域信号加窗截取,再通过齿数和式(2)可以计算啮合齿序特征[12],

图5 齿根裂纹行星轮 图6 齿根裂纹太阳轮Fig.5 Planet gear with tooth root crack Fig.6 Sun gear with tooth root crack
根据重排齿序拼接重构振动分离信号。
根据行星轮系传动理论,实验时输入转速为1 000 r/min(转速脉冲测量)。计算出各理论特征阶次,对于振动分离信号,得到的是行星轮或太阳轮相对行星架旋转的整圈信号,研究中采用的参考信号为行星架转速脉冲信号,因此根据式(4),(6),(8)计算出各阶次:a.行星齿轮箱啮合阶次lm为71阶;b.行星轮故障阶次lpr为3.55阶;c.太阳轮故障阶次lsr为2.535 7阶。
4.2 信号分析
4.2.1 正常状态数据
在无故障行星齿轮箱上采集得到的正常状态振动信号用于行星轮和太阳轮故障对比分析,其时域波形如图7(a)所示,图7(b)为对应的转速脉冲信号局部放大,图7(c)为对应的转速曲线。由转速脉冲计算的转速曲线可以看出其存在转速波动。
4.2.2 行星轮故障特征提取
在装有故障行星轮的齿轮箱上采集的振动信号如图8(a)所示,图8(b,c)分别为对应的转速脉冲和转速曲线。
若对行星轮故障在时域进行包络加窗同步平均,得到时域振动分离信号如图9所示,无法看出故障应对应的周期性冲击特征。
若对行星轮故障信号不进行加窗同步平均,得到的原始信号包络谱如图10所示,可以看出原始信号包络谱其谱线复杂,且突出谱线为行星架转频4.715 8 Hz,但故障特征频率无法辨识。

图7 正常振动信号Fig.7 Normal vibration signal

图8 行星轮故障信号Fig.8 Planet gear fault signal
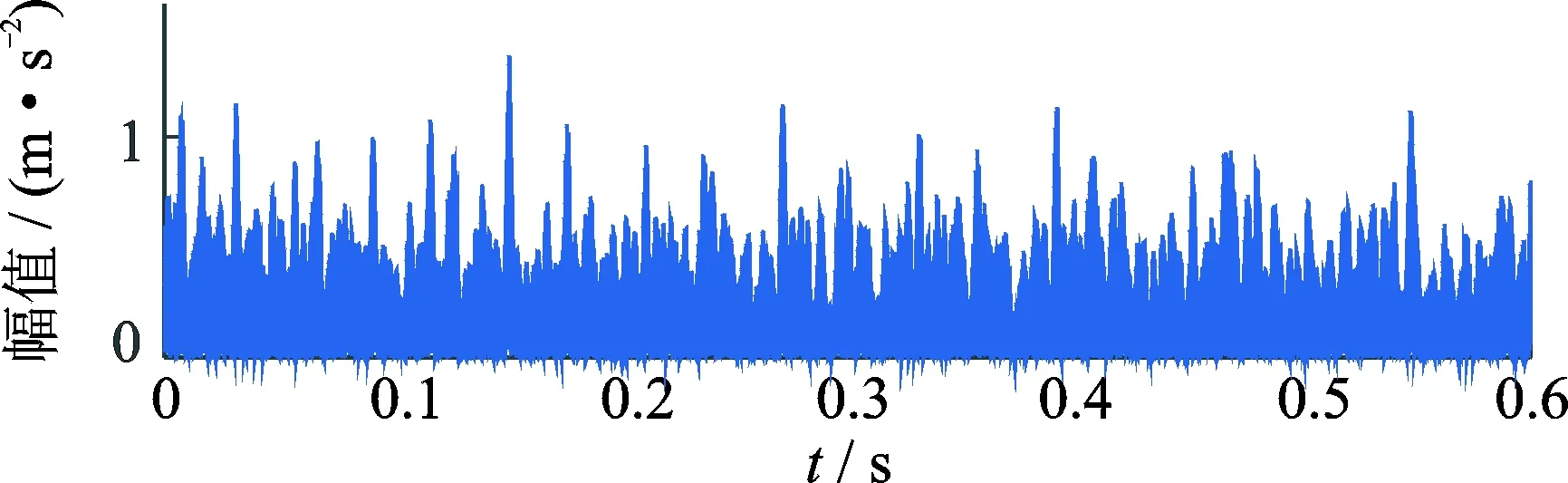
图9 行星轮时域振动分离信号Fig.9 Time domain vibration separation signal of planet gear
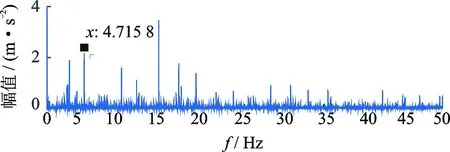
图10 行星轮故障原始信号包络谱Fig.10 Envelope spectrum of original signal of planet gear fault
应用笔者所提方法得到的行星轮故障包络信号平均振动分离信号如图11(a)所示,其中根据谱峭度得到中心频率为6 800 Hz,带宽为800 Hz。对正常状态下使用同一滤波参数进行,对应正常状态下的包络信号平均后振动分离信号如图11(b)所示。通过阶比分析得到的阶次谱如图12所示。
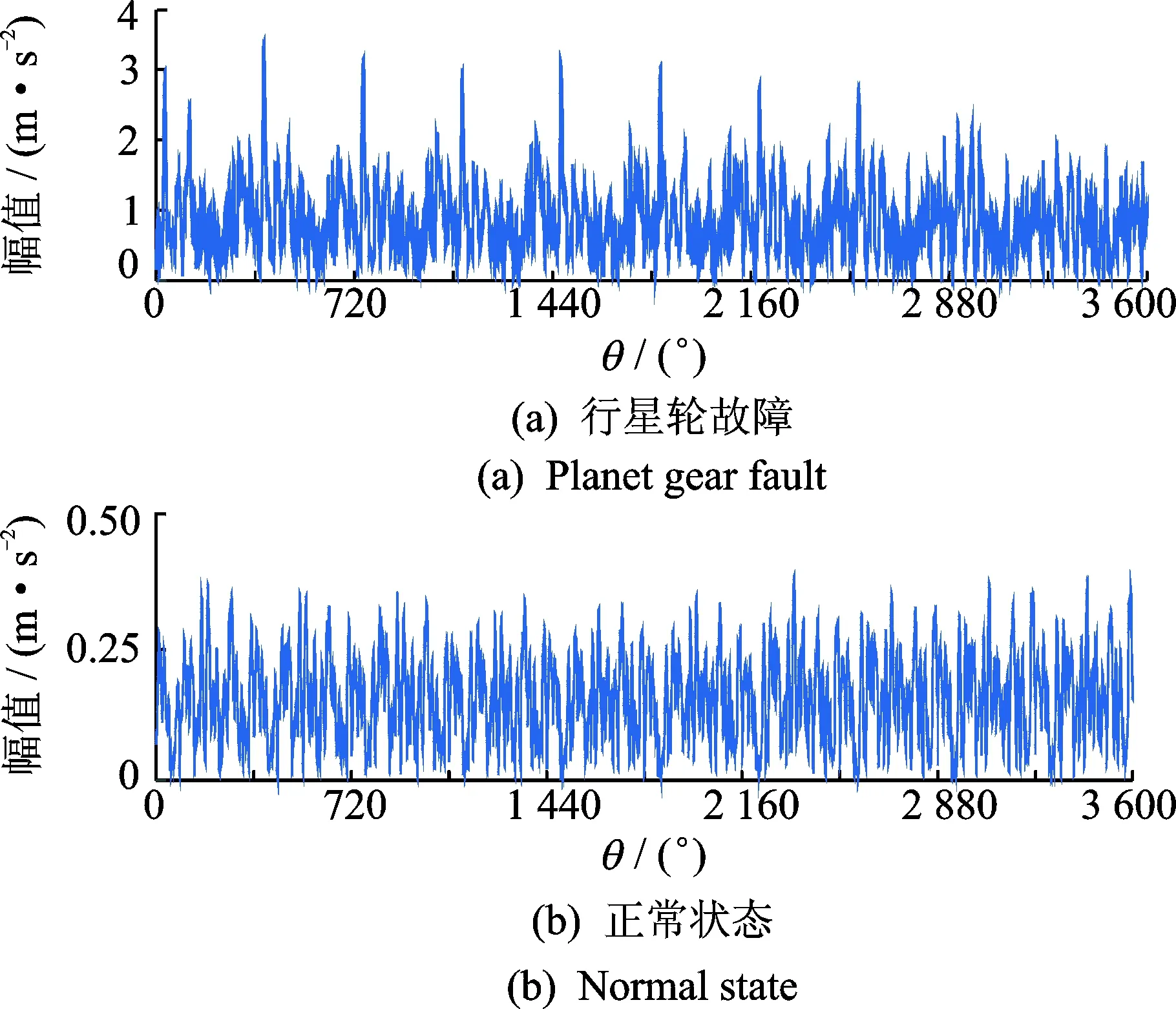
图11 振动分离信号Fig.11 Vibration separation signal

图12 行星轮故障与正常状态下故障特征阶次对比Fig.12 Comparison of fault characteristic order of planet gear fault and normal state
分析图11(a)的振动分离信号可以看出行星轮故障状态下其振动分离信号每周期中存在一个突出峰值,而对于图11(b)正常状态下其信号峰值不明显。由对应的阶次谱(见图12)看出,阶次谱中出现行星轮故障阶次3.55阶,且其谱线单一,清楚的对应于行星轮故障阶次,对比行星轮故障状态下与正常状态下其幅值差异较大。
不难看出,笔者所提方法可降低噪声及其他阶次成分的干扰,使故障特征更加明显。综合分析可说明基于包络信号的角域加窗同步平均方法对于行星齿轮箱故障特征提取的有效性(对太阳轮故障提取有同样优势)。
4.2.3 太阳轮故障特征提取
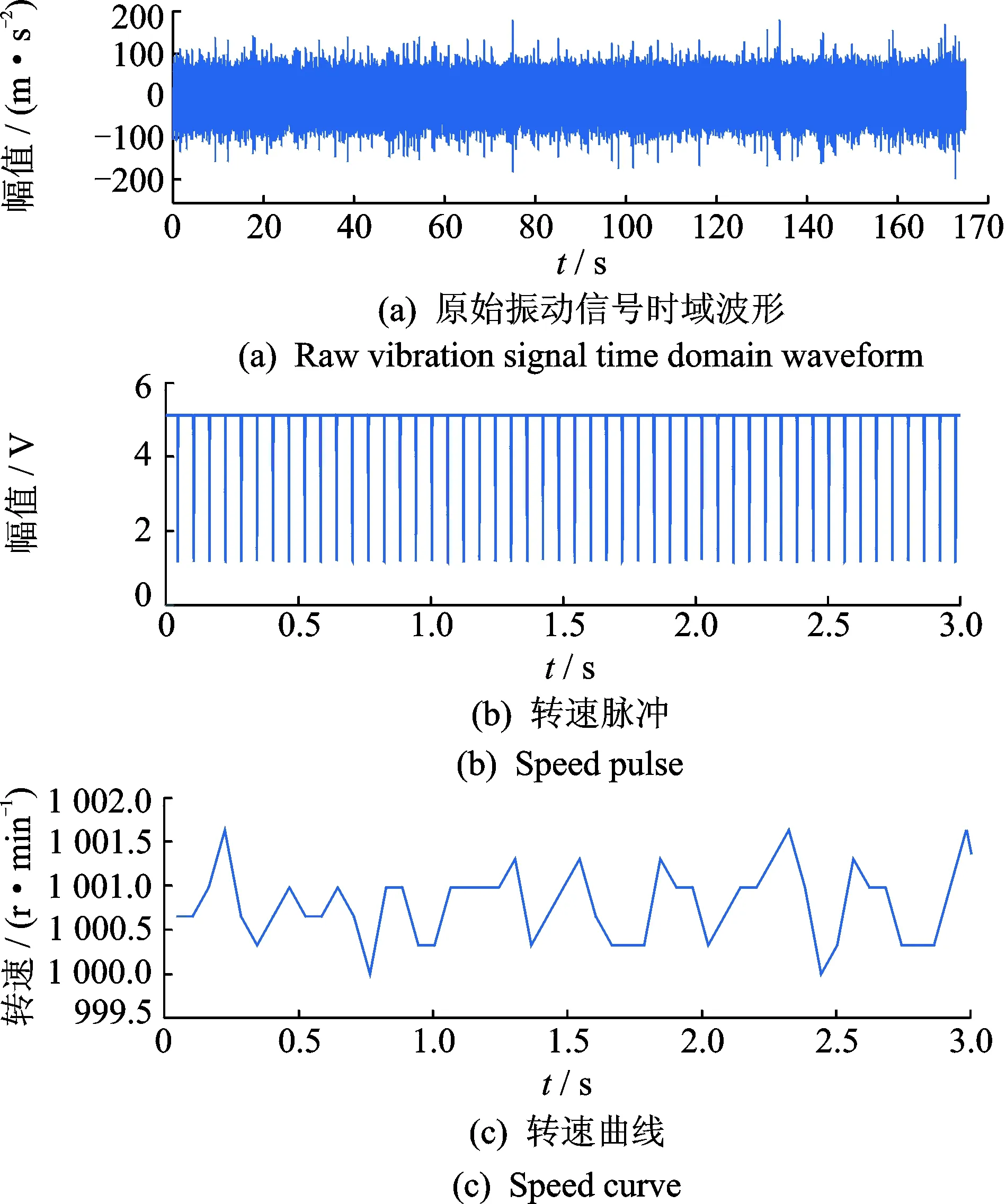
图13 太阳轮故障信号Fig.13 Sun gear fault signal
在装有故障太阳轮的齿轮箱上采集的振动信号如图13(a)所示,图13(b,c)为对应的转速脉冲及转速曲线。由转速脉冲计算的转速曲线可以看出其存在转速波动。同样,应用所提方法得到的太阳轮故障包络信号的平均后振动分离信号如图14(a)所示, 其中根据谱峭度得到的中心频率为8 400 Hz,带宽为800 Hz。对正常状态下使用同一滤波参数进行,对应正常状态下的包络信号平均后振动分离信号如图14(b)所示,阶次谱如图15所示。
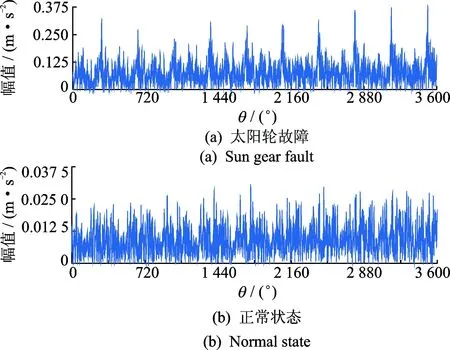
图14 振动分离信号Fig.14 Vibration separation signal
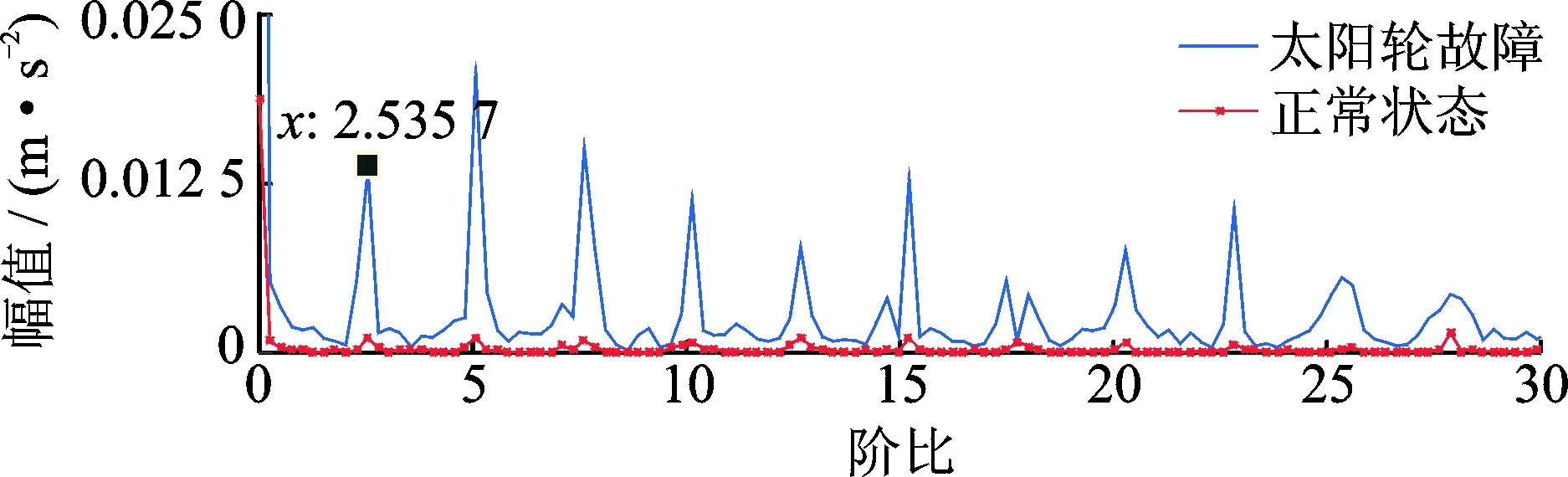
图15 太阳轮故障与正常状态下故障特征阶次对比Fig.15 Comparison of fault characteristic order of sun gear fault and normal state
同样,对于太阳轮故障状态下,基于包络信号的平均后振动分离信号每周期存在一个突出峰值,且其阶比谱中太阳轮故障阶次2.535 7阶突出,谱线清晰,对比太阳轮故障状态下与正常状态下,其故障状态下故障阶次幅值更加突出,综合说明基于包络信号的加窗振动分离与同步平均对提取行星齿轮箱故障特征的有效性。
5 结 论
1) 基于谱峭度的包络分析能自适应提取共振带参数,对于齿轮的早期弱故障,包络分析能有效提取其故障特征;
2) 阶次跟踪通过对原始信号进行等角度重采样转为准平稳信号,不仅能有效避免时变载荷导致的转速波动对频谱分析的影响,并且选择合适的重采样点数能提高对信号加窗的精度。
3) 对于行星齿轮箱振动信号传递路径的时变性,通过对单个行星轮或太阳轮得加窗振动分离可以有效避免行星齿轮箱振动时变传递路径的影响;
4) 对振动分离信号进行同步平均,能有效降低噪声和无关分量的干扰。
综合分析能清晰提取出行星齿轮箱故障特征,并通过实验验证基于包络角域加窗同步平均的行星齿轮箱早期故障特征提取的有效性。
