模块约束力对雷达阵面热变形的影响规律研究
2019-05-08陈维康郑克非
陈维康,郑克非
(合肥工业大学 仪器科学与光电工程学院,安徽 合肥 230009)
有源相控阵雷达(active phased array radar,APAR)天线阵面在工况下会受到环境温度、T/R组件热源等的影响而发生热变形,导致天线的电性能下降[1]。因此,实现雷达阵面热变形的准确预测和补偿已成为相控阵雷达设计和运行中的重要步骤[2]-[3]。
热变形的影响因素众多,除了温度、尺寸、应力等因素外,研究还发现夹紧方式以及夹紧力对零件热变形也有较大的影响[4]-[5]。APAR结构复杂,通常由多个模块拼接组合而成,各模块之间存在一定的机械拼接约束力,但由于结构复杂及材料的不同,并不能保证理想的约束力。国内外对于模块约束力对雷达阵面热变形的影响研究较少。
文章通过对雷达阵面模块施加不同的约束力进行热特性研究,建立了关于模块约束力的阵面热变形模型,对文献[6]中未考虑约束力不同时的雷达阵面热变形预测模型进行了补充,验证了约束力模型的适用性,为雷达阵面热变形误差分析以及工程结构设计提供了参考。
1 雷达阵面热变形实验
文章以雷达阵面平板结构为研究对象,自行设计了一套雷达工作模型,通过Leadway-V450型数控加工中心在线检测系统,对不同模块约束力下的雷达阵面热变形进行测量,以研究模块约束力对热变形的影响规律。
1.1 实验装置
雷达实验模型包括天线平板、加热器、测点立柱和支架,其装配图见图1,天线平板尺寸为400mm*360mm,其矩形槽下方安装有模拟T/R组件功耗的加热器,对加热器施加不同的电压来控制温度场变化。天线平板上安装有长方体立柱作为测量标准件,共55根,用以测量天线平板的热变形。20个温度传感器的测点位置按照图1中圆柱体位置进行分布。

图1 雷达模型装配图及温度传感器分布
1.2 实验方案
文章在雷达四个角处分别利用约束力调整装置进行紧固,利用扭矩扳手(精度±2%,测量范围100-500N·m)控制支架上紧固螺钉的旋紧扭矩,产生不同的垂直作用力在支撑柱上进行压紧,实现对雷达阵面施加不同约束,然后通过数控机床的在线检测技术实现热变形量的测量,以探究不同模块约束力对雷达阵面热变形的影响。
因阵面X向和Y向热变形具有相似的性质,本文只研究不同模块约束力对X向热变形的影响。共进行6批次实验,记为H1,H2,...,H6,H1~H6组实验雷达模型左侧角1和角4处的旋紧扭矩相同,皆为500N·m,右侧角2和角3的旋紧扭矩相同,6批次实验右侧旋紧扭矩分别为0,100,200,300,400,500N·m。
1.3 实验结果
限于篇幅,只比较在20V加热电压下雷达阵面XY下热变形,H1~H6批次实验阵面中间行11列测点的X向热变形如图2所示,随着右侧模块约束力增大至左侧的模块约束力的过程中,X向热变形曲线逐渐下移,最后关于直线X=0中心对称。宏观上表现为左右模块约束力相差越大,阵面整体热变形偏移越大。

图2 H1~H6批次实验中间行各测点的X向热变形
假设在某一加热电压下,M行N列测点的X热变形量记为:
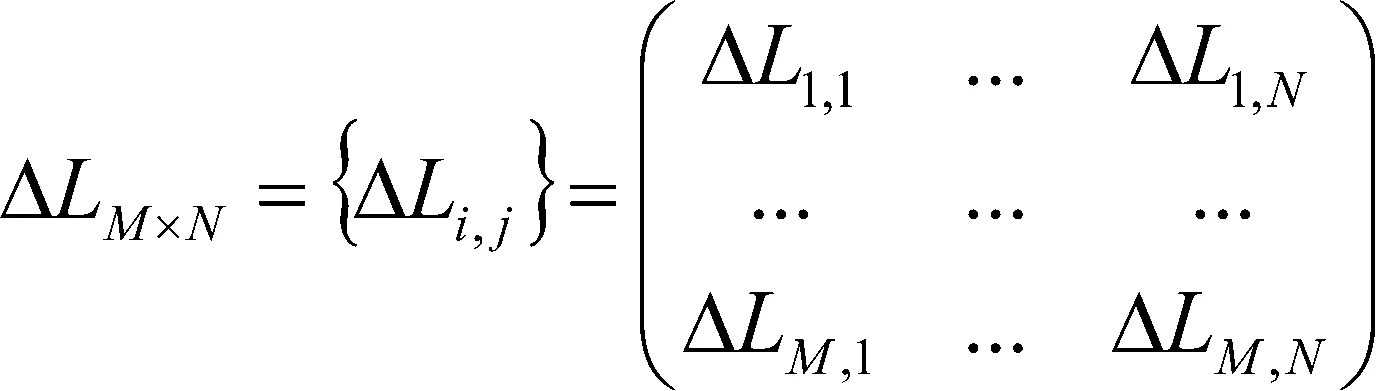
(1)
依据传统热变形理论公式ΔL=α·L·ΔT,阵面的X向平均热膨胀系数为:

(2)

根据式(2)计算H1~H6批次实验雷达阵面X向平均热膨胀系数,得到的X向平均热膨胀系数最大值为13.57×10-6℃-1,最小值为12.4×10-6℃-1,相差不超过10%,可认为模块约束力对阵面X向平均热膨胀系数无影响,即模块约束力对X向热膨胀量无影响。
2 模块约束力影响规律分析
2.1 热变形中心列偏移理论
当零件一侧模块约束力不变另一侧模块约束力发生改变时,零件总的膨胀量几乎不变,但膨胀趋势随模块约束力发生改变,本文将这种热膨胀趋势称为热偏移,阵面热变形由热膨胀和热偏移构成,如式(3)所示。其中,δ为实际变形,δL为膨胀量,δd为偏移量。
δ=δL+δd
(3)
模块约束力对膨胀量影响较小,因此只需研究偏移量与模块约束力之间的关系。我们将初始状态下阵面的中心列称为几何中心列O0,热变形量为零处的位置称为热变形中心列OX。当不发生热偏移时,热变形中心列与几何中心列重合,当由于模块约束力而发生热偏移时,几何中心列不再与热变形中心列重合,将阵列偏移量与测点列数N-1之比称为热变形中心列偏移比ωx,即:
ωx=(Ox-O0)/(N-1)
(4)
2.2 热变形中心列偏移模型
由Ox定义可知,Ox即为图2中X向热变形曲线与横轴焦点的横坐标。由于X向热变形曲线近似直线,阵列上测点的位移均匀变化,因此可通过最小二乘拟合得到测点X向热变形关于阵列序数的线性方程如下所示:
δx=k·Nx+b
(5)
其中δx表示X向热变形,Nx表示列数序号。
然后计算得到Ox,即:
Ox=-b/k
(6)
为了得到雷达阵面关于模块约束力的X向热变形中心列偏移模型,本文定义约束比dF来量化模块约束力的变化,即:
(7)
其中,FL表示左侧的旋紧扭矩,即角1和角4的旋紧扭矩,FR表示右侧旋紧扭矩,即角2和角3的旋紧扭矩。
对各批次实验X向热变形进行最小二乘法拟合,然后根据式(5)和式(6)得到Ox,再根据式(4)得到各批次实验不同加热电压下的X向热变形中心列偏移比ωx,对热变形中心列偏移比曲线进行拟合,结果如图3所示。
得到X向热变形中心列偏移模型为:

(8)
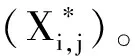

(9)
其中,i=1,2...M,j=1,2,...N。

图3 不同约束比下热变形中心列偏移比
2.3 模型验证
为了检验上述热变形中心列偏移模型的适用性,重新安排3种模块约束力情况进行热变形实验,3批次实验分别记为G1~G3,均在角1和角4施加500 N·m旋紧扭矩,角2和角3分别都施加0,150,300 N·m旋紧扭矩。
选择20V加热电压,利用热变形中心列偏移模型式(8)和修正公式(9)对文献[6]中雷达阵面热变形预测结果进行修正,得到修正前后的模型预测结果如表1所示。表中δm表示最大预测误差,ΔLm表示最大变形量,P表示百分比精度,其计算公式为:

(10)
根据表1的精度比对结果可以明显看出,不考虑模块约束力时,模型预测精度较低,平均精度仅为54.2%,考虑模块约束力并进行修正后,模型对于热变形的预测精度平均可达73.2%,提升了30%左右。验证了中心列偏移模型的适用性,拓展了热变形理论。

表1 热变形模型预测精度结果
本文研究仅仅是初步的,只对X向热变形规律进行了分析,存在一定的局限性,更进一步的研究及论证正在进行中。
