由覆杯实验引申的压强问题研究

2019-05-07张立娜胡君辉全文文

物理实验 2019年4期

庄党，张帆，张立娜，胡君辉，杜婧，全文文，阳丽

(广西师范大学物理科学与技术学院，广西桂林 541004)

在初中物理实验中，覆杯实验因为取材方便、操作简单、现象直观一直被用作验证大气压存在的演示实验. 将玻璃杯装满水，在杯口盖1张纸，然后倒置，可以发现水被纸片托住. 实验时，一般认为玻璃杯一定要装满水，不然实验就会失败[1]. 在实际教学中发现，有些学生在不装满水的情况下，同样的方法倒置依然可以托住水. 为此，本文针对该问题展开了分析.

1 实验模型

图1(a)是实际做实验过程中，观察到的实验现象：液面上方会有凹层，而在液面和纸张接触处会有1层水层. 根据图1(a)，可以做如图1(b)所示的实验模型图来讨论.

(a)实物实验 (b)模型图1 覆杯实验

1.1 液面附加压强

由图1(b)模型可知，纸张和水杯之间形成附着层. 液面下降的原因不是因为附着层，若不考虑附着层，不妨设下降高度为Δh，此时液面上部形成凹层. 由于Δh非常小，且下降的水全部分散于附着层内，因此可以认为水的高度h不发生变化. 液面上方形成的凹面. 因为弧度非常小，可以认为此凹面是半径为X的球体的一部分，如图2所示. 液块受到3部分的力作用：1)通过液块边线作用在液面的张力；2)由底部作用于液面引起的附加压强所导致的压力；3)液块受到的重力，与前两部分力相比，小得很多，可忽略不计[2].

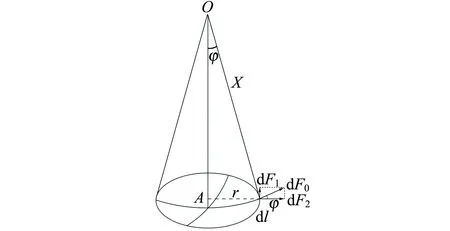
图2 液体凹面受力示意图

通过边线每一微段dl作用在液体表面的张力dF0=αdl，可以分解成垂直于底面的分力和平行于底面的分力：

dF1=dF0sinφ=αdlsinφ,

(1)

dF2=dF0cosφ=αdlcosφ.

(2)

这两部分力中，平行于底面方向的各个分力dF2由于方向都垂直于轴线OA，由对称性可知，其合力为零；而垂直于底面方向的分力dF1，方向相同，合力大小为

(3)

根据平衡条件，液面下表面受到的力源于液面上下的压强差[3]，即F1=Δpπr2，于是可以得到凹面的附加压强[2]为

(4)

1.2 纸张和附着层的平衡条件

在此模型中，纸张能够被吸附，是因为纸张和液块分别满足了平衡条件. 在纸张和杯子之间会形成液体的附着层，如图3所示. 由于液块自身的重力非常小，可忽略不计. 因此，液块受到的力可以分成2部分：一部分是由于纸张的重力所引起的拉力F,另一部分是液体内部给小液块的力. 液体内部的力又可以分为3个区域:附着层内部Ⅰ、液体内部Ⅱ和表面层内部Ⅲ. 区域Ⅰ作用的力是沿着纸张表面的压力N，区域Ⅲ作用的力是水的张力T, 区域Ⅱ作用的力的大小与T和N相比太小可以忽略不计. 因此附着层的小液块受到的力分别为N,F和T.

图3 附着层与纸张受力示意图

由平衡条件可以得到，

Tcosθ=N,

(5)

Tsinθ=F.

(6)

由(5)～(6)式可知，决定平衡的条件为：液体的张力、接触角θ以及纸张的重力[3]. 液体的张力T由液体本身的性质决定，接触角θ由液体和纸张的相对性质决定，对于给定的液体和纸张，接触角θ是确定值. 因此，要使实验现象得以实现的前提，取决于覆盖物的质量m以及液体与覆盖物的本身属性.

2 杯内水柱平衡条件

由图3可知，在杯子没有被倒置之前. 杯内的空气体积为V，当杯子被倒置时，液面会形成凹面. 此时杯内的空气体积将会变大，而增加的体积是以X为半径高为Δh的球冠，其大小为

(7)

倒置之后，杯内空气体积为V1=V+V0. 根据气体的物态方程[4]

pV=nRT=K,

(8)

式中，p为气体压强，V为气体体积，n为气体分子数，R为普适气体常量.

2.1 支撑水柱的压强分析

根据实验过程可知，在倒置前后，温度的变化可忽略，分子数并未发生改变[5]，因此K为常量. 此时，杯内空气的气压值为

(9)

外界大气压值为

(10)

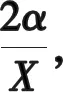
(11)

A点与B点的高度差为h. 此时，B点的压强为

(12)

根据流体静力学的基本原理，流体静止时等高的两点的压强相等. 忽略纸张厚度，即pC=pB=p0，于是有

(13)

由(9)式～(10)式和(12)式～(13)式可以知道水柱高度与压强的关系

(14)

由(14)式可知，支撑起水杯中水柱的原因为：弯曲液面内外的压强差及由于杯内空气与外界大气的压强差[6].

2.2 水柱平衡的实际数据分析

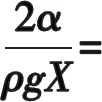
(14)式中后面部分，由(8)式可得

(15)

对于(15)式中，由于球冠的体积边缘较小，可以近似认为它的体积是以半径为r、高为Δh的圆柱的体积[6]，即

(16)

由此(15)式可以化解为

(17)

实际实验中，l的高度约5 cm，假设Δh的高度为1 mm，综合(14)式和(17)式可以得到，杯内空气与外界大气的压强差能够支撑起的水柱高度为20.2 cm. 可见，这是撑起水柱的主要原因. 1标准大气压可以支撑起10 m左右的水柱，而该实验的水杯高度不会超过0.1 m. 由(17)式只要增加的凹面的体积不超过原有体积1%，形成的压强差就可以支撑起水柱[7].

3 实验验证

3.1 实验材料与实验方法

实验材料：普通玻璃杯1个(高13.5 cm)，不透水卡片1张，自来水. 为了清楚地看到玻璃杯内的空气柱长度，在玻璃杯壁上标刻度.

为了演示玻璃杯中空气柱的高度不会影响“覆杯实验”的成功，分别进行了9组实验，分别控制水柱的高度为玻璃杯的1/16，1/8，2/8，…,直到整杯水[8].

3.2 实验现象

分别拍摄1/16,1/8,2/8,3/8,4/8,5/8,6/8,7/8以及满杯水9种情况下覆杯实验的演示现象,如图4所示. 以上该实验均获得成功，由式(14)和(17)也可知杯内空气与外界大气的压强差能够支撑起的水柱高度为20.2 cm，在此实验中即使满杯水也未超过20.2 cm. 同时，1标准大气压可以支撑起10 m左右的水柱，在实验中远远没有达到10 m高度，且每次增加1/8的水量带来的凹面体积的增加并未超过原有体积的1%. 因此，在实验中液面高度的变化并不影响覆被实验的成功.