金属材料疲劳短裂纹扩展研究综述
2019-05-07秦建兵
秦建兵
(中国航空工业集团有限公司 西安飞机工业(集团)有限责任公司,西安 710089)
0 引 言
近几十年来,随着科学技术的发展,疲劳断裂力学的理论也得到了进一步发展和完善。普遍认为,材料与结构的疲劳失效过程包括裂纹萌生、扩展直至断裂三个阶段,而裂纹萌生及其早期扩展消耗了至少90%的寿命[1],因此对早期疲劳损伤的研究十分必要。
传统的疲劳及断裂观点认为:当裂尖的应力强度因子ΔK<ΔKth时,裂纹就不会扩展,但近来的研究发现:在0.5 mm裂纹长度的区域内,无论是传统的疲劳概念还是使用线弹性断裂力学的理论,都不能很好地描述这一区域裂纹的形成和扩展规律。由于在这一区域内的裂纹较短(一般为晶粒尺寸量级),所以称其为短裂纹。短裂纹通常具有下列独特的扩展行为[2-7]:
(1) 短裂纹的应力强度因子门槛值不同于长裂纹,通常比其低。当应力强度因子值相同时,短裂纹扩展更快且以较高的速率起始。
(2) 在等幅载荷作用下,短裂纹起始扩展速率较高,随着裂纹进一步扩展,扩展速率下降。然后根据所加载荷的大小,或形成非扩展裂纹,或随着裂纹长度的增加,其扩展速率上升直到长裂纹范围的独特“V”型扩展规律。
(3) 由于短裂纹发生在晶粒尺寸级,所以材料的微观结构,晶界的取向,缺口及裂尖塑性区的影响,使得材料的各向同性及均匀连续介质力学的假设等存在较大的偏差。
短裂纹的研究,不仅对裂纹起始定义的改进、光滑试件的疲劳极限Δσe和疲劳裂纹扩展应力强度因子门槛值ΔKth之间的关系、解释疲劳减缩系数Kf和应力集中系数Kt之间的差别等起着关键的作用,而且对全面进行结构件的全寿命估算、改进材料的冶炼加工、提高材料的疲劳性能参数及进行可靠的安全寿命设计等都有重要意义。
本文对近几十年来国内外关于疲劳短裂纹扩展的理论模型和影响因素进行综述,重点讨论短裂纹扩展弹性模型的不足,引入弹塑性力学参数J-积分来描述短裂纹尖端的应力场,并对新的研究方法进行论述,把宏观力学的方法和微观力学的概念结合起来分析短裂纹的扩展规律;针对短裂纹阶段所特有的非扩展裂纹,探讨其形成原因,解释缺口试件疲劳强度减缩系数Kf与理论应力集中系数Kt的区别;介绍试验件的形式、缺口塑性区、微观结构和试验环境等因素对短裂纹扩展规律的影响;通过对实验中的主裂纹和次裂纹扩展规律的研究,进一步证实短裂纹独特的“V”型扩展规律,并通过观察裂纹扩展的整个过程,尝试利用裂尖应力场的变化,来解释短裂纹的非扩展裂纹行为。
1 短裂纹的扩展模型及理论分析
1.1 短裂纹扩展模型的弹性和塑性分析
短裂纹问题提出以后,由于对它的起始扩展机制不很清楚,人们首先从长裂纹扩展的理论出发,使用线弹性断裂力学的方法对短裂纹问题进行工程修正。由于短裂纹长度很短,材料的均匀连续介质力学假设失效,直接用线弹性力学参数-应力强度因子ΔK-来描述短裂纹的扩展产生的误差将会很大。为使短裂纹的扩展规律更接近长裂纹,以便使其适合于工程应用,M.H.EI.Haddad等[8]把疲劳极限和断裂的临界状态结合起来提出了本质裂纹ao的假设模型。即:在实际的裂纹长度基础上增加考虑一个材料长度ao来作弹性应力强度因子计算,并模拟短裂纹的门槛性质。
(1)
其中:ao可由ΔKth和Δσe计算,当a→0时,ΔS→Δσe,ΔK→ΔKth,且F=1[8-9],则:
(2)
R.A.Smith等[10]给出了相同的结论,认为裂纹扩展规律简单地服从等幅应力和等幅ΔKth曲线,两条直线的交点为ao。即:当a 材料常数ao的引入是通过将疲劳和断裂的临界状态结合起来,对短裂纹能在应力强度因子ΔK<ΔKth条件下扩展及短裂纹在相同的应力强度因子下以较高的速率扩展进行了修正,使其接近长裂纹的扩展规律。从式(1)可见,ΔK仍随着裂纹长度的增加而增加,因此只能得到da/dN随ΔK单调上升的结果,它仍不能解释短裂纹的“V”型扩展特性。由于短裂纹所处的区域使得线弹性断裂力学不再适用,人们开始使用弹塑性断裂力学的方法来分析短裂纹问题。人们在本质裂纹模型的假设基础上,使用弹塑性力学参数J-积分来描述短裂纹尖端的应力场。裂尖的应力场分为弹、塑性两部分: (3) (4) 则: ΔJ= ΔJe+ΔJp=2πF2(a+a0)· (5) J-积分的使用使得长短裂纹扩展规律的差别得到了进一步的修正,但它仍不能从本质上解决短裂纹的扩展特性。目前的研究认为:ao并非为一材料常数,它与所加的应力水平,构件的形状等参数有关[11]。即: a0=f(Δσ,Kt,Δa,B,A) (6) 式中:B为试件的厚度;A为常数。 K.Tanaka等[12]认为:由于短裂纹本身与材料的微观结构有着密切的联系,在研究应力门槛值附近的裂纹扩展特征中发现:本质裂纹ao与材料的晶粒尺寸及滑移带的长度也有一定的关系。裂尖的滑移带是被晶界切断的,裂纹扩展的应力强度因子门槛值条件是由被晶界阻止的裂纹能否进入相邻晶界的晶粒内部来确定的。K.Tanaka等用微观和宏观结合的办法,对短裂纹的门槛应力强度因子及其扩展特性作了进一步的修正,得: (7) (8) 由式(1)和式(7)得: (9) ΔKcb=(4Gγ/α)1/2 (10) 式中:γ为物体的真实表面能;G为剪切模量;α=1-v。 在短裂纹范围内,当ΔK=ΔKcb时,裂纹扩展,并将形成的塑性条带留在裂纹面的两侧。同时,塑性位移增量的影响将改变裂尖应力场的分布。在裂纹扩展的距离小于等于裂尖的塑性区尺寸时,裂尖的真实应力强度因子为: ΔKee=ξ·ΔKI (11) 式中:ξ将随着裂纹的扩展而单调下降,若裂纹的增量为δa,则: (12) 式中:f*为ξ近似地取(1-2β/πa)1/2前所必须穿过的塑性区尺寸。只有0≤δa≤f*·rp时,式(12)才成立。 在短裂纹扩展初期,裂纹几乎不张开,此时的闭合应力很小[17-18],且被缺口塑性区包围着,而随着短裂纹的进一步扩展,裂尖塑性区也变大,产生的残余应力,使得裂纹张开,闭合应力不再是常数,而是随着裂纹长度的增加而增加,当其增加到某一临界值时,闭合应力达到最大值,然后基本上保持这一常数进入长裂纹区域[18]。除了塑性区,裂纹面粗糙度引起的裂纹闭合对裂纹扩展门槛值影响很大,包括裂纹内生成的氧化物碎屑[19]。W.L.Morris[17]使用2219-T851铝材料对晶粒尺寸量级的短裂纹扩展作了定量分析,结合裂尖张开位移CTOD与闭合应力的关系描述了闭合应力对短裂纹扩展的作用。在短裂纹区域内,裂尖处的闭合应力是各向异性的,当裂尖距晶界较远时,裂纹的张开位移较小,闭合应力几乎为零,而当裂尖接近晶界时,裂尖的张开位移较大,闭合应力值也较大。且: (13) 由dugdale模型在小范围屈服条件下,有: (14) (15) (16) 使用有效应力强度因子参数ΔKeff=Kmax-Kop来描述短裂纹的扩展特性发现:裂纹扩展速率的理论值比实验值略大。崔振旗等[20]用实验的方法研究了残余压应力对ΔKeff的影响,并对上面的公式进行了修正,ΔKeff=(Kmax+λKr)-Kop,理论值与实测值吻合较好。残余压应力使得裂纹闭合力提高,最大应力强度因子降低,ΔKeff势必会减少,导致裂纹扩展速率降低。短裂纹在穿过残余压应力影响区后,裂纹扩展率会立刻变大,残余压应力对短裂纹扩展的影响随着应力比的增加而减弱[21]。长短裂纹扩展速率之间的差别也得到了进一步的修正。 短裂纹的起始与裂尖滑移带有着密切的联系,材料缺口处滑移带的挤入挤出为微裂纹的形成提供了显微缺口,微裂纹通常在这些平行的,沿最大剪应力方向平面上形成,并沿着滑移带的主方向扩展[22]。当微裂纹成核并扩展时,随着外力的增加,在邻近的几条滑移带将产生交变减聚力,使得裂纹形成一种拉链式的扩展形式[23-24]。对于缺口试件,在应力水平刚刚高于应力门槛值时,缺口附近的某一晶粒内将产生滑动位移,当裂纹沿着滑移带成核后,核裂纹的位错应变能将达到一临界值ΔU0。K.Tanaka等[12]将此时的裂纹长度定义为初始裂纹长度,应力循环数为初始寿命,且: (17) 式中:l为滑移带长度。 若滑移带从缺口处形成,且被最近的晶界切断,则: (18) 式中:t为缺口深度;ρ为缺口半径。 令单位面积内的断裂能为ωs,初始寿命为Ns,则 2Ns·ΔU0=4·l·ωs (19) 在2t>ρ,2t>l时: (20) 由于材料的微观结构是各向异性的,单纯的由位错和滑移来分析短裂纹的扩展是比较困难的,因此有必要将宏观力学的方法和微观力学的概念结合起来分析短裂纹的扩展规律。当滑移带在一个晶粒内形成并移动时,就可以形成一个裂尖的塑性位移是沿一个或几个应力轴倾斜的微裂纹。K.S.Chan等[25]提出:在晶粒内的裂尖不产生屈服(与J.Weertman的结论相同),裂尖的塑性区尺寸一般为裂纹长度的一半,并且这一区域的应力场由裂尖的应力控制。当裂尖前缘的塑性应变足够大时,裂纹向前扩展且塑性应变与ΔK之间服从幂指数关系: Δεp=C·(ΔK)n (21) 式中:C,n为常数。K.S.Chan认为:在裂纹初始时,其张开位移为一常数,C,n的确定与此有关。 晶界对裂尖塑性应变的影响取决于相邻晶界的取向。裂尖的滑移带被晶界切断后引起的累积塑性应变为: (22) 式中:X为裂尖距最近晶界的距离;K(φ)为取决于相邻晶界取向的函数。 (23) 函数K(φ)可以由含有裂纹的晶粒及其相邻晶粒内的剪应力计算,设它们分别为τA和τB,若τB>τA,则: (24) 将式(24)代入式(23)得: (25) 裂尖的塑性累积应变Δεp为: (26) ΔN=ε*/Δεp (27) (28) 在大多数缺口试件中,短裂纹区别于长裂纹的另一个重要因素就是非扩展裂纹。在缺口处形成的短裂纹,扩展一段后,当应力水平足够小时,就停止扩展,形成短裂纹阶段所特有的非扩展裂纹[27]。非扩展裂纹也存在于光滑试件中。长、短裂纹的非扩展裂纹明显不同,在相同的应力强度因子幅下,只要ΔK<ΔKth,长裂纹就不扩展,而短裂纹会扩展一段距离后再停止扩展。非扩展裂纹延长了短裂纹的寿命,解决短裂纹的非扩展裂纹问题对裂纹扩展寿命计算,解释疲劳强度减缩系数Kf与Kt的差别有着重要的意义。 短裂纹的非扩展裂纹不仅与应力门槛值有关,而且与缺口的形状和几何尺寸也有较大的关系[28-29]。S.J.Jr.Hudak[27]指出:缺口试件疲劳强度减缩系数Kf与理论应力集中系数Kt是有一定区别的。Kf与Kt的区别有可能就是由于缺口试件的非扩展裂纹而引起的。在试件完全破坏区域内,存在着一个最低的应力极限,它与Kt无关。但在非完全破坏区域内,存在一Kf的临界值Kf(th),当Kf M.H.EI.Haddad等[8]使用本质裂纹模型对非扩展裂纹的门槛值分析得: (29) (30) 他们的结果表明:当Kt>Kt(th)时,则ΔSth-a曲线的峰值向右移动,当Kt (31) (32) 非扩展裂纹的绝对上限为: (33) 且: 在缺口处产生非扩展裂纹还有一些其它的影响因素,由于短裂纹能在低于长裂纹定义的门槛值应力强度因子时扩展,所以它首先扩展一段距离,而后在与裂纹尺寸和缺口应力有关的ΔKth值以下停止扩展;塑性区的残余应力抵消了部分外载的作用,裂纹的反复张开不足以使短裂纹扩展,但裂尖的应力状态由平面应力状态转变成平面应变状态,屈服应力提高,裂尖的塑性应变减小,材料的循环硬化,晶界及晶粒的尺寸,晶粒的排列所引起的裂纹扩展方向的改变等都是产生非扩展裂纹的可能原因[31]。 从目前的研究知道,影响短裂纹扩展的因素很多。载荷、缺口塑性区,金属的微观结构和试验环境等都对短裂纹的扩展有较大的影响。 应力比R对短裂纹的初期扩展及门槛值也有一定的影响,应力比R的增加将造成初期扩展速率和门槛值的下降[32]。但也有的研究认为,应力比R对门槛值的影响是由于裂尖塑性区的残余压应力所造成的。 材料的微观结构对短裂纹扩展也有较大的影响。K.Tanaka等[12,33]研究了低碳钢材料中短裂纹近临界扩展时晶粒尺寸的影响时指出:裂纹扩展速率随晶粒尺寸的增加而下降,而临界应力强度因子幅值却与晶粒半径的平方根成线性增加。在临界区附近,大晶粒尺寸材料中裂纹扩展速率较慢。当短裂纹在晶粒内部扩展时,材料处于各向异性状态,晶粒边界的取向及晶界阻力对裂纹扩展有较大的影响。随着裂尖距晶界越近,晶界对裂纹扩展的阻力越大[27]。在晶界与裂纹扩展方向垂直时,其阻力最大,而当晶界与裂纹扩展方向平行时,晶界的阻力最小。 众所周知,对于长裂纹,由于裂纹长度比塑性区尺寸大得多,缺口塑性区对裂纹扩展影响较小,而对短裂纹,缺口的塑性区把整个短裂纹及其尖端塑性区全部包围在内。这样使得短裂纹完全处于塑性状态,裂纹在外力的作用下根本不张开或张开很小。缺口塑性区同样对短裂纹产生较大的残余应力,也对裂纹扩展起到了一定的阻碍作用,也是造成短裂纹“V”型扩展的原因之一[34]。 缺口的几何参数的不同对短裂纹的扩展速率影响是不同的。在同样的材料中,缺口半径较小时,裂纹多数呈“V”型扩展,而缺口半径较大时,裂纹扩展速率一般随着裂纹的增加而增加[28]。同样缺口半径ρ也决定缺口塑性区尺寸的大小和应力—应变梯度[35-36]。 试验的环境不同,短裂纹的扩展速率也有一定的差别。应力强度因子相同时,温度会促使裂纹扩展加快。活性气体较惰性气体会加速裂纹扩展,并且比空气中有更低的门槛应力强度因子幅值[37]。 前面介绍了一些研究短裂纹扩展特性的理论方法、模型及影响短裂纹扩展的因素。但大家都知道,要想更好的探讨短裂纹的扩展机制及验证这些理论模型,精确的测量裂纹长度是非常重要的。如果得不到精确的裂纹长度,也就无法研究短裂纹的扩展机制及其扩展规律。 目前在短裂纹试验中所采用的检测方法有:直流、交流电位法、显微镜直接读数法、声发射法、复型法和涡流跟踪法等。近来的研究表明复型法和声发射法测量的精度较高(一般可检测到0.01 mm的裂纹长度),这两种方法目前也常被采用。声发射技术具有很高的灵敏度,它可以获得单个原子的重新排列和成百万个原子键的破裂所产生的声发射信息。在试验过程中,由位错、裂纹扩展、马氏体相变等产生的声发射信号由传感器接收,经过放大、滤波,最后由记录装置记录下来。但由于声发射时信号中不仅有裂纹扩展而产生的声发射信号,而且也含有背景噪音,机械噪音等噪音信号。尽管可以用滤波和设置门槛电平的方法消除大部分噪音信号,但仍有一部分信号被传感器接收与真正的信号混在一起。并且目前最困难的是声发射信号的标定。 复型技术一般分为一次复型和二次复型,通常都采用一次复型的方法。复型可以比较清晰地得到试件表面的真实状况,测量精度也较高。这种技术比较容易掌握,一般在取得复型片后,使用高倍光学显微镜放大,拍照,然后从后向前读数,这样可以较容易地抓住主裂纹,但这种方法工作量大,若复型搞得不好会歪曲地反映裂纹长度,有时会使裂纹与气泡混在一起而无法读数。采用复型技术,对试件的表面光洁度要求较高,否则对以后判断裂纹长度会有较大的影响。在复型过程中,必须停机采样,这样频率的变化及试验件的卸载对裂纹的扩展都有一定的影响。 显微镜直读法也是一种较常采样的方法,通常可在试件的两侧各放一台50~100倍的读数显微镜。这种方法比较简单实用,而且能比较直观地得到短裂纹的一些扩展现象。但这种方法的误差较大,若用高倍数显微镜,尽管读数精度较高,但由于其聚焦范围太小,不易抓住短裂纹。若用的显微镜倍数较小,其本身的分辨率就较低,加上肉眼读数的误差就会使整个读数误差增大。直流、交流电位法,涡流跟踪法,由于缺口的边缘效应较大,因此在缺口试件中不大采用。 本文前面综述性地介绍了研究短裂纹的部分理论模型与分析方法,并对影响短裂纹扩展的一些因素做了简介。但这些理论都没有对短裂纹扩展机理和它的裂尖应力场给予很好的解决。通过所做的一些实验,对短裂纹的独特扩展规律提出下列两点看法。 在许多实验中都观察到这样一种现象,在缺口处起始的裂纹不止一条而是有多条裂纹。在实验开始时,我们可以较容易的发现:在缺口的表面可出现几条微裂纹,但经过一定的循环后,其中一条裂纹成为主裂纹向前扩展,而其余的裂纹不扩展或扩展非常慢。在主裂纹扩展以后,其扩展速率逐渐下降,同时另一条与主裂纹相近的裂纹(我们称它为次裂纹)也开始扩展,当它的长度与主裂纹近乎相等时,主裂纹开始加速扩展,而次裂纹成为非扩展裂纹。从能量的角度分析看,由于外力所施加的能量是一定的,它除一部分使材料产生塑性变形外,其余的就成为使裂纹扩展的断裂能,由于多裂纹的出现,特别是次主裂纹,它们与主裂纹同样分享使裂纹扩展的断裂能。这样主裂纹所得到的断裂能必然相应减少,使其扩展速率下降。这是否可以认为是促使短裂纹扩展速率下降的原因有待于进一步研究,在许多试验中,同样观察到短裂纹出现非连续的跳跃扩展现象[38]。一般短裂纹是从接近缺口表面的第一个晶粒开始扩展的,经过一定的循环后,短裂纹可以在相邻的几个晶粒内部同时出现。当它们穿透晶界后,几条微裂纹就可能连接到一起,突然跳跃式的形成一条相对较长的短裂纹。使得短裂纹的扩展速率突然加快。 实验显示,短裂纹在表面形成并扩展,顺着表面晶粒的方向和晶界的位置,然后才成为穿透裂纹的。在平面应力状态下,裂尖的塑性应变相对较高,而且闭合效应几乎没有,使得短裂纹具有在相同应力强度因子下有较高的初始扩展速率。随着裂尖应力状态的转变,裂纹的塑性区增加,闭合应力也同样发生变化。短裂纹初始时,裂纹张开位移ΔCOD≈弹性位移,此时闭合应力相应较低,在裂纹明显出现以后,ΔCOD下降并逐渐上升,也就使得闭合应力逐渐增加[20]。一般认为这可能是由于缺口塑性区的移动而产生的残余应力引起的结果。 通过宏观和微观,力学和材料学的结合,对短裂纹的扩展机制及其“V”型扩展规律做了研究。这对进一步完善疲劳和断裂力学的方法,使疲劳的概念和断裂力学的理论的有机结合有一定的促进作用。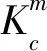
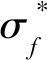
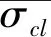
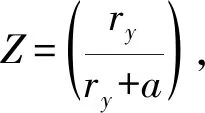
1.2 短裂纹扩展模型的宏观和微观分析


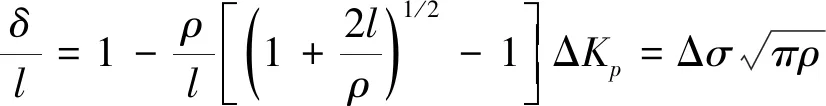
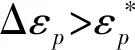


2 短裂纹的非扩展裂纹
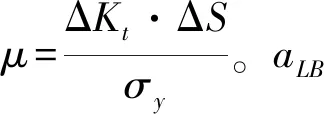

3 影响短裂纹扩展的因素
4 短裂纹扩展的实验方法
5 讨 论
5.1 短裂纹扩展的实验分析
5.2 裂尖应力场
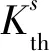
6 结束语
