基于时频切片分解的时变系统参数识别

陈淇，史治宇，张杰

(南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016)

0 引 言

系统的时变问题指的是，因外部环境影响或自身结构特性，系统的动力学参数随时间变化的问题。随着人类社会的进步和科学技术的发展，工程结构的时变问题在包括土木工程、机械设计、航空航天等多个领域日渐突出。例如，高超声速飞行器在高速飞行过程中，因自身的气动布局和气动加热等问题导致的颤振现象[1]；汽车经过桥梁时，因为附加质量导致的车桥系统集中质量随汽车位置而改变；人工智能机械手臂在旋转过程中，因结构本身的改变，而导致的空间质量分布和刚度分布的改变等。因此，时变系统参数识别方法的研究有着重要的学术价值和工程价值。

为了寻找到一种可靠的时变系统参数识别方法，国内外学者做过诸多努力。20世纪80年代，A.Grosssman等[2]为了研究地震波的时频特性首次提出了小波的概念；而后，W.J.Staszewski等[3]基于小波的各种改进方法被用于动力学参数识别领域。许鑫等[4]在连续小波积分的基础上，把振动微分方程转化为以加速度项表达的小波变换式，并提出了基于加速度响应的连续小波变换的时变系统参数识别方法。N.E.Huang等[5-6]提出了经验模态分解法(即EMD法)，该方法与M.Feldman[7-8]的Hilbert变换相结合，便是著名的Hilbert-Huang变换(HHT变换)，可用以识别时变系统参数。1997年，K.Liu[9]在状态子空间模型的基础上，引入了自由响应时变系统参数识别，并于两年后将该方法推广至受迫响应下的时变系统参数识别。状态空间的方法后续还经历了诸多发展[10]，例如庞世伟等[11-12]引入的投影估计法、M.Raffy等[13]对渐进性统计误差的估计等。这些改进的方法都对状态空间方法的研究与发展做出了重要贡献。

上述识别方法在不同层面上均有一定的局限性。因为涉及小波基函数的选取，所以小波的方法需要有一定的信号先验信息，是非自适应的。而HHT变换尽管对所有信号都具有自适应性，但其本身是一种经验式的信号分解方法，存在模态混叠、缺乏正交性证明等缺陷[14]。状态空间的方法涉及矩阵计算，存在计算量大等问题。

在吸取了短时傅里叶变换和连续小波变换的优点下，Yan Zhonghong等[15]提出了频率切片小波变换的方法；钟先友等[16-17]将其用于处理爆破分析和故障诊断等信号分析方面的问题。本文则吸取切片小波基可在任意时频区间对信号进行切片的优点，提出基于时频切片分解的时变系统参数识别方法，用以识别时变系统随时间而变化的模态参数。

1 理论介绍

1.1 时变振动系统基本理论

假设系统为n自由度的时变系统，在第k个自由度上受到脉冲激励作用，则系统的振动微分方程为[18]

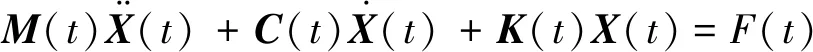
(1)

式中：F(t)为系统所受到的第k个自由度上的脉冲激励；M(t)、C(t)和K(t)分别为系统质量矩阵、阻尼矩阵、刚度矩阵，它们的数值都随着时间而改变。

设阻尼为比例阻尼，则可引入X(t)=Φ(t)q(t)对系统进行模态解耦，Φ(t)=[φ1(t),φ2(t),…,φn(t)]，为固有阵型矩阵；q(t)=[q1(t),q2(t),…,qn(t)]T，为模态坐标矩阵。解耦结果为

(2)

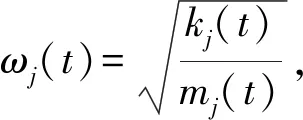
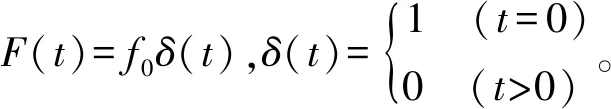
(3)

根据模态叠加法，第p自由度上的系统位移响应xp(t)为各阶模态位移响应xpj(t)的叠加，即

(4)

xpj(t) =φpj(t)qj(t)

=Bpj,k(t)e-ζj(t)ωj(t)t×

(5)

1.2 切片小波基及其相关理论

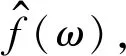
(6)

那么，可以利用切片小波基函数对f(t)进行时频变换[8]，变换结果为

(7)

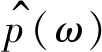
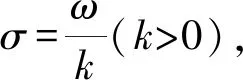
(8)

式中：k为与ω、u独立的变量，定义为时频分辨系数，用以表征时频切片窗的时频伸缩尺度。

根据海森堡测不准原理，时频切片窗口的频率边长和时间边长的乘积为一常数，相对精准的时间分辨率将以牺牲频率分辨率为代价，相对精准的频率分辨率将以牺牲时间分辨率为代价，而时频分辨系数k的数值将决定时频分解对频率或时间的敏感度。

对于时频分解的结果，可利用逆变换进行信号还原，得到原信号在任意时间区间和任意频率区间内的重构信号，对于时间切片区间(t1,t2)和频率切片区间(ω1,ω2)，重构信号的表达式为

(9)

综上，利用切片小波基可在任意时频区间对信号进行切片和其逆变换重构还原快速便捷的特点，本文引入针对时变系统的时频切片分解参数识别方法。

1.3 基于时频切片的时变系统参数识别

由时变系统基本理论可知，n自由度的时变系统脉冲激励下第k自由度上的响应激励可表示为n个单模态信号的线性叠加，而这n个单模态信号中分别包含了系统的n阶模态信息。因此，时变响应信号的识别是解决时变问题的关键。传统的EMD方法利用经验模态分解算法处理响应信号，经验式地将响应信号分解为多个本征模态函数进行识别，尽管有较好的自适应性，却存在本征模态函数正交性难以证明等问题。本文则引入时频切片分解的方法来解决响应信号的识别问题，具体时频切片分解和后续识别过程如下：

对振动系统采集到的第p自由度上的时变位移响应xp(t)，选择合适的切片小波进行整个时间域的时频分解，可得到其时频分布能量图，再根据信号的时频分布特性，划分出n个时间频率区间，接着依据这n个时间频率区间分别对位移响应xp(t)进行时频分解，得到n个独立的时频分解后的信号，分解出的这n个信号即为组成系统脉冲激励响应的n个单模态信号。

(10)

式中：r(t)为时频切片分解的残差项。

(11)

式中：Apj(t)为解析信号的幅值函数；φpj(t)为解析信号的相位函数。

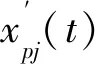
(12)

进一步可得：

(13)

则解析信号幅值图InApj(t)-t的斜率为单阶模态频率和阻尼比乘积的相反数-ζjωj，解析信号相位图φpj(t)-t的斜率为单阶模态阻尼频率ωdj。

基于时频切片分解的时变系统参数识别方法流程图如图1所示。

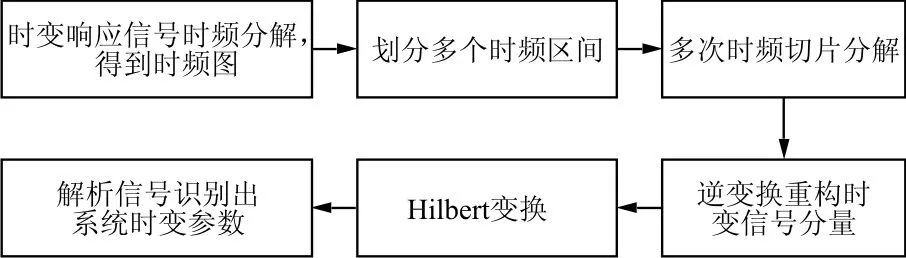
图1 基于时频切片分解的时变系统参数识别方法流程图

2 仿真分析

为了更直观地展现基于时频切片的时变系统参数识别方法，设计一个三自由度的弹簧—阻尼—质量块结构仿真实验，如图2所示。

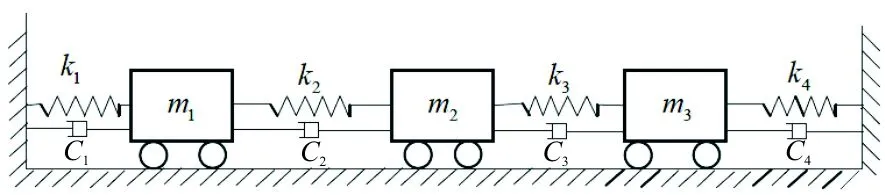
图2 仿真结构示意图

初始位移、速度、加速皆为0，结构初始参数为

结构参数随时间而变化，变化规律为

(14)

激励为脉冲激励，作用在质量块3(m3)上，使用Newmarkβ算法计算10 s内结构各个自由度上的位移响应。选取第二个自由度上的位移响应进行时频切片分解，得到时频分布图如图3所示。

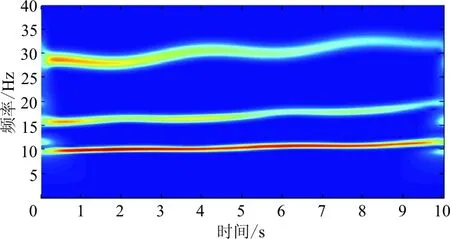
图3 位移响应信号的时频分布能量图

从图3可以看出：信号中主要包含了三阶能量分量，按照自然频率段5～13、13～20、25～35 Hz划分出三个频率切片段，时间切片长度皆为10 s；这三个切片片段再次对响应信号分别进行三次时频切片分解，得到三段独立的时频信号，如果以时频图来展示这三段信号，将得到与图3类似的三幅各自频率段上的时频，故本文不再重复展示。

对于时频切片分解的结果，即三段独立的时频信号，分别通过逆变换算法进行信号重构，得到三段时域上的重构信号，也就是三阶单模态时域信号，如图4所示。

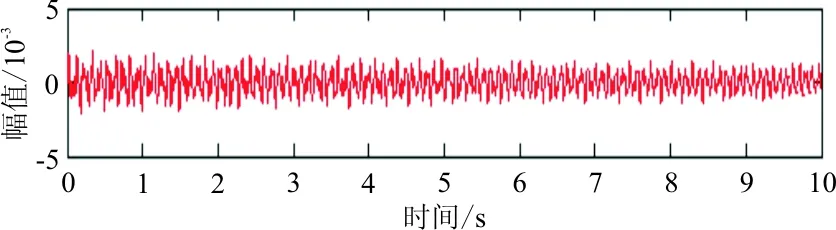
(a) 原信号

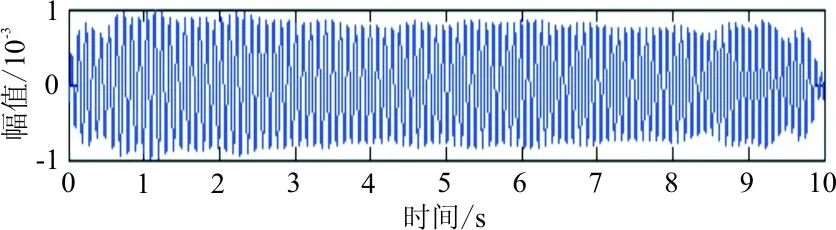
(b) 切片1信号重构

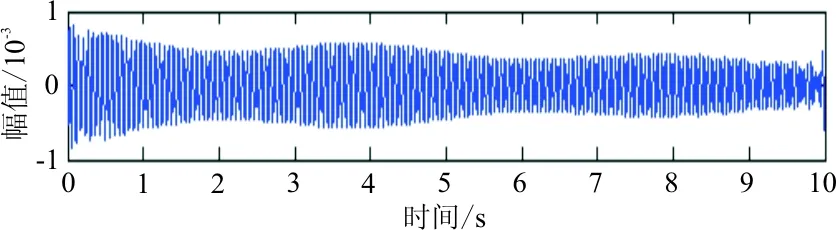
(c) 切片2信号重构

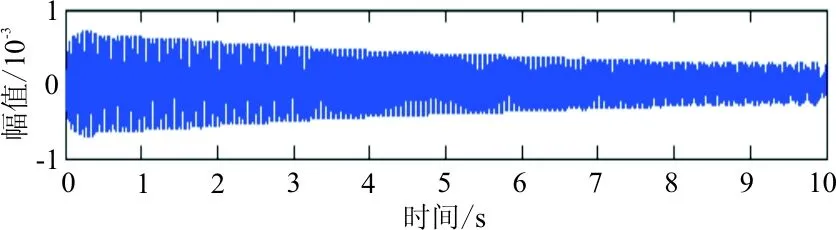
(d) 切片3信号重构

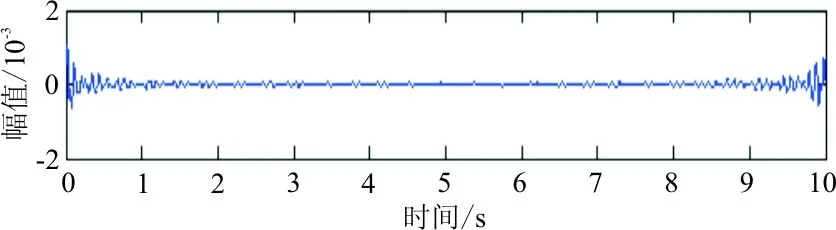
(e) 残差信号

从图4可以看出：响应能量在时间区域上分布较均匀，第一阶能量较强，第二、第三阶能量相对弱些，但和第一阶能量大致在数量级上不存在差异，表明本次仿真包括参数设置、激励点/响应点位置选取、激励方式的选择都较为合理，比较完整地激发出了结构的三阶能量信息。残差信号为原信号减去重构分量信号所得。

对于重构的分量信号，依次进行Hilbert变换识别系统各个时间上的阻尼频率，以圆频率形式表示，并和理论计算的阻尼频率相比较，如图5～图7所示。

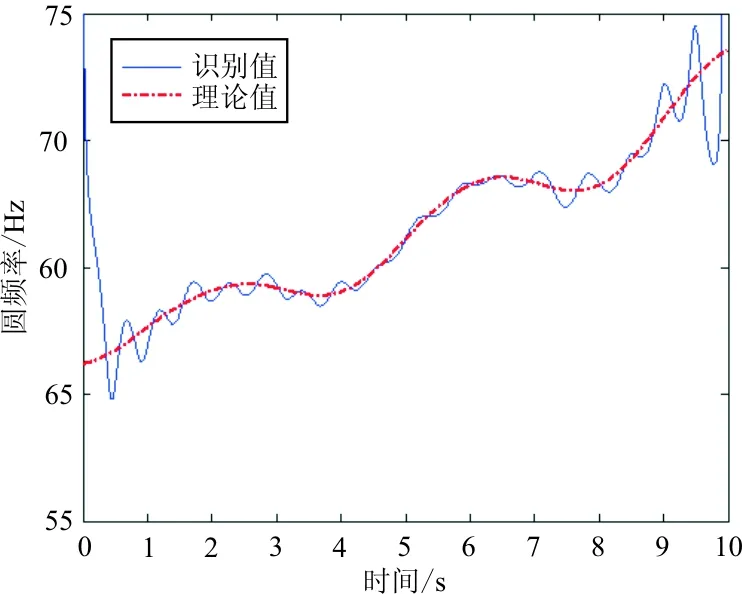
图5 第一阶阻尼频率识别值和理论值对比图

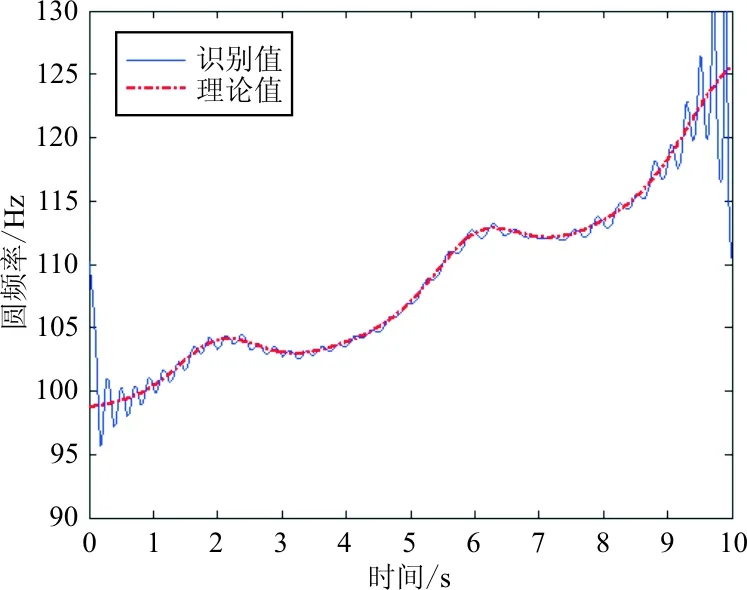
图6 第二阶阻尼频率识别值和理论值对比图

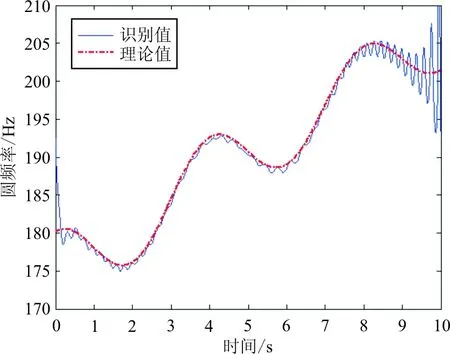
图7 第三阶阻尼频率识别值和理论值对比图

从图5～图7可以看出：除了无法避免的边界效应外，识别出的三阶阻尼频率和理论三阶阻尼频率随时间变换趋势一致，数值基本重合。

为了进一步展示识别误差，使用平均相对百分比误差MAPE，计算公式为

(14)

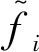
本文识别出的一阶、二阶和三阶模态阻尼比的MAPE分别为1.080%、0.740%和0.043%。考虑到不可避免的边界效应造成的误差在MAPE计算中的占比并不小，因此该识别方法在大部分时间域中的误差水平要比MAPE展示的误差水平还要低得多。可以认为基于时频切片分解的时变系统参数识别方法拥有非常好的识别精度和实用价值。

3 结 论

(1) 基于时频切片分解的时变系统参数识别方法可以将多自由度时变系统的响应信号进行切片分解，将原本的位移响应信号分解为多个单模态信号。再经过逆变换完成时域上的重构，对于重构后的各阶信号，通过Hilbert变换提取信号瞬时频率，从而识别出时变结构的各阶频率。

(2) 该方法时频切片分解的逆变换算法不依赖于切片小波基的选取，使得信号逆变换非常方便快捷，相较于传统的小波方法，具有计算效率高的优点。

(3) 尽管信号经过多次切片小波分解，但是每次切片分解和重构过程都是独立进行的，各阶误差不会相互影响，故抗噪能力强。

(4) 端点处的误差是小波类方法通有的端点效应造成的，可以通过延长采样时间，让端点效应产生在一个不关心的时间区域中来解决。

(5) 仿真算例展示了时频切片分解的时变系统参数识别方法的具体步骤和效果，验证了其可行性，表明其识别精度高。