13.56 MHz线圈天线信号与能量传输匹配系统研究*

朱道恒，秦 学

（贵州大学 大数据与信息工程学院，贵州 贵阳 550025）

0 引 言

随着无线电技术的迅猛发展，便携式设备的多样化令ISM频段的可用区间愈发匮乏。为保证移动设备的基本通信功能，13.56 MHz频段的信号与能量传输技术为这一研究提供了新的方向[1]。这一近场交互式交换方式已经有了比较成熟的应用，如二代身份证件和校园卡。但是，不同设备所需要的线圈天线的尺寸各不相同，若要适配新的设备，传统的方法是在现有的成熟模板基础上，利用软件对天线结构尺寸进行优化[2]。或者为实物模型设计新的电容电阻匹配电路，并在矢量网络分析仪中进行优化。这样不仅会产生大量的科研成本，而且会因细小的匹配误差造成整个匹配系统功亏一篑[3]。所以，为了降低科研人员的研发成本，本文提出了一种基于有限元分析软件HFSS设计的两款线圈天线，并用在端口处模拟匹配电路。

如图1所示，利用匹配电路使其工作于50 Ω匹配环境中，使其分别能够在13.56 MHz电磁频率中有效传播信号与能量。

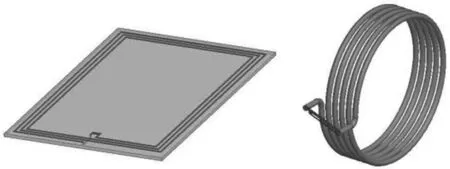
图1 线圈天线

其中，平面线圈天线的尺寸在以长80 mm、宽50 mm、贴片宽0.5 mm、间隔1 mm为核心参数的标准上下波动。同理，弹簧式线圈天线半径为20 mm，内径为1.5 mm。值得一提的是，此处线圈天线尺寸并无固定要求，满足设备所需即可。根据这里设计的两款线圈天线，本文将对其添加适配电阻与滤波电容等方法，因为每一个线圈天线都可以视为电容、电感和电阻的混联产物。所以，本文将从并联与串联等效电路两个角度出发，为线圈天线调整频率至13.56 MHz。

1 天线理论基础

1.1 天线理论

在电磁波近场交互中，衡量一个线圈天线性能好坏的标准是其等效电感值[4]。通过实验验证可以得出，等效电感值越大的线圈，天线在相同功率时所能产生的磁通量也越大[5]。因此，信号能够传输得更加稳定，能量的传输效率也越高。一般线圈天线的最佳工作电感范围为500～2 000 nH。线圈天线电感值与线圈匝数之间的关系式为：

式中，L为线圈天线的电感估值，单位nH；l1为线圈天线所在环的周长，单位cm；D1为线圈天线的内径宽度，单位cm；K为线圈系数，一般取值为K=1.47；N为线圈天线的匝数。

根据电感范围和线圈天线的尺寸，可计算得出线圈匝数N的最佳取值范围为3～5匝。因此，本文将以3匝平面线圈天线和5匝弹簧线圈为例进行讨论。

13.56 MHz线圈天线虽然属于一种近场交互天线，但其仍然满足天线所具备的性质，即同样满足传输线理论[6]。所以，如果确定线圈天线的基本构造，其等效电感L、欧姆损耗电阻值Ra以及自谐振并联阻抗值都会随即确定。

电感L可由天线smith圆图[7]中的参数计算得出，计算公式为：

式中，z为Smith圆图中天线在f频段处的阻抗参数；Im为取阻抗虚部，即线圈天线抗性。

可以根据公式：

结合自谐振并联阻值，推导出天线线圈处于工作频率13.56 MHz时的谐振电阻值。

每个线圈天线都可以等效为一个并联电路或者串联电路，如图2所示。

图2 线圈天线等效电路

等效电路中，电容、电阻和电感具备如下关系：

结合图2，式中Cpa、Lpa以及Rpa分别为线圈天线并联阻抗参数，Ra、La和Ca为串联阻抗的参数。

1.2 匹配电路理论

因为不同的线圈天线等效电路的等效阻值不同，所以其具备的优势也不相同。并联电路具有高阻值，所以更适合信号的加载与传输；串联电路中阻值较小，会大大减小电阻带来的热损耗，也就更适合近场的能量交换[8]。

所以，本文将从并联与串联电路匹配两个角度出发，运用HFSS分别搭建RLC外接等效电路进行研究。

若线圈天线选用并联等效电路，其所需适配并联电阻可由式（5）推导得出：

式中，Rp13.56为线圈天线在13.56 MHz时的并联谐振电阻值，并结合并联电路电阻公式：

同时，按国际ISO14443标准的Q值[9]，可以将二端口网络入射总电阻求出。根据并联电路规则式（6）推导出并联型匹配电路所需要的外接电阻阻值，且根据Smith圆图的优化匹配功能，按照串、并联电路需求，推导出外接电容的串并联形式和容值。

与并联形式的匹配电路不同，串联匹配电路虽然依然需要借助Q值，但因为等效方式有着明显的不同，所以求得的阻值也不相同。这就是串联形式的匹配电路更加适合能量传输的根本原因。

根据串联等效电路总电阻的推导式，线圈天线等效为串联电路的形式，可以先通过HFSS等仿真软件计算得出线圈天线在所求频率下的串联等效电阻Ra。串联电路电阻关系式为：

式中，Rs_t为从二端口网络接入的等效总电阻，Rs_m为线圈天线串联等效电路所需匹配的外接串联电阻，Ra为所求频段线圈天线等效电阻。

2 并联匹配

参考图2（a）中平面线圈天线，先用HFSS软件构建天线参数化模型，再设置正确的空间边界条件，选择扫描扫频范围1～80 MHz。运行仿真后，调用Smith圆图工具，结果如图3所示。

图3 线圈天线Smith圆图

通过分析Smith圆图，可从图中标注得出，m2位于X轴，线圈天线表现出纯电阻特性，即抗性可忽略。又因为在设置HFSS激励端口时输入阻抗为50 Ω，由Z62.41=133 7-115.24 i，可求出并联自谐振频率为62.4 MHz，电阻值为Rpa=66.8 kΩ。

将所得数据代入式（3），得到平面线圈天线在频率13.56 MHz时的并联谐振电阻阻值为Rp13.56=32.7 kΩ。根据国际ISO14443标准，将Q=10代入：

式中，ω为线圈工作点处的谐振频率，L为线圈电感，由式（2）结合Smith圆图结果可算出Rp_t=1.27 kΩ，最后将式（6）做恒等变换，得：

将得出的数据整理分类，并代入Smith设计图中构造并联匹配电路，如图4所示。

图4中粗线条为匹配过程，可得出在并联匹配中，并联电容Cp_1=48.5 pF，串联电容Cp_2=47 pF。

将匹配电阻值与所求出的匹配电容值代入HFSS软件中，其匹配电阻与匹配电容以RLC边界条件设置于平面线圈激励端口两端。

通过扫频分析，并查看其S11，如图5所示。

图4 并联匹配电路

可以明显看出，线圈天线在13.56 MHz处有明显的频率响应。因此，该并联匹配系统对平面线圈天线有着很好的匹配特性。

3 串联匹配

因为并联电阻Rp_a更适合携带信息，而串联电阻Ra较小，相同功率下的热能损耗也会较小。所以，运用串联等效电路的弹簧线圈更适合无线能量的传输[10]。同样，在HFSS软件中构建如图1（b）所示的弹簧线圈天线的参数化模型，结合图3中m1点处的阻抗参数，又因为Smith圆图输入的匹配电阻为50 Ω，所以Z13.56=0.004 7+2.499 i，再结合式（2）可得到等效损耗热电阻Ra=0.235 Ω，等效电感L=1.46 μH。

图5 S11响应

结合ISO14443标准，Rs_t=ωL/Q=12.7 Ω。在串联电路中，电阻如式（10）所示，将Rs_t结果代入：

得到Rs_m=12.5 Ω。由于实际工作电路中并不存在此阻值的电阻，故取其阻值最接近的电阻进行计算，即Rs_m=12 Ω。

将所得串联匹配电阻Rs_m代入Smith圆图中，并设置好相关参数，可得到串联匹配电容如图6所示。

图6中标记部分为系统匹配路径，由此求得匹配电路所需并联电容的容值大小，其中并联电容Cs_1=47 pF，串联电容Cs_2=46 pF。将所得匹配电路结构模型按数值大小代入弹簧线圈的HFSS模型中，并设置正确的RLC边界条件，最终可从Smith圆图中得出弹簧天线的匹配状态，如图7所示。

图6 串联匹配电路

图7 Smith圆图匹配状态

从图7可以清晰看出，弹簧天线在13.56 MHz频率下几乎呈纯电阻状态，即虚部几乎为0。因此，该串联匹配系统可以对弹簧天线进行适配。

下面继续构建弹簧天线传输的参数化模型，如图8所示，以便更好地观察其传输特性。

图8 天线传输模型

利用HFSS软件的参数优化功能，得到弹簧天线传输效率与传输距离的关系即观测S21参数，如图9所示。

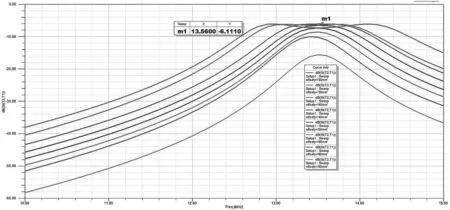
图9 S21与线圈距离关系

可以看出，在13.56 MHz频率下，弹簧线圈天线的能量能够得到有效传输，证明该串联匹配电路确实对弹簧线圈天线起到了优化效果。

4 结 语

通过分别对两种结构不同的线圈天线进行并联匹配和串联匹配电路设计，可以看出两种天线都取得了良好的匹配效果。与传统的天线优化过程不同，设计者为了得到所需频率响应的天线，往往考虑从天线结构设计方面来改进，不仅无法满足当今通信设备多结构化的特性，而且优化过程也需要花费大量的人力和物力成本。通过外接匹配电路的方法，不仅可以在模拟仿真中完成，而且可节省大量的实验设备花销，同时只需增加一个简单的设置就可以模拟出仿真环境。因此，将等效电路等效为HFSS中的RLC边界条件，具有快捷、低成本和高精确度的效果。