基于ARIMA的网络流量建模及预测研究*

盛 虎，张玉雪

（大连交通大学电气信息工程学院，辽宁 大连 116028）

0 引 言

网络流量的实时分析对于网络流量监控、网络资源优化、网络拥塞避免和网络安全策略具有重要的意义[1-2]。基于网络流量时间序列的建模分析是进行网络流量数据研究的一种主要方法，已经广泛应用于网络流量预测和网络性能评价。研究人员可以通过建立准确的流量模型描述网络流量特性，从而优化网络拓扑结构、完善网络协议，提供可靠的服务质量保障。

传统的网络流量模型是在平稳随机过程假设的前提下，线性差分方程基础上建立的滑动平均自回归（Auto-Regressive and Moving Average Model，ARMA）模型[3-4]。网络流量ARMA模型可以有效分析短时间内流量稳定的网络数据，但对于存在网络异常的长时间网络流量数据却并不适合，其主要原因在于ARMA模型建立的前提是被分析数据是平稳随机过程。现实的网络流量数据大部分是非平稳的，但经过有限次差分后可以转化为平稳数据，因此在研究过程中学者提出了回归积分滑动平均（ARIMA）模型[5]，广义自回归条件异方差（Generalized AutoRegressive Conditional Heteroskedasticity，GARCH）模型等。其中ARIMA模型因为其实现简单，可以描述网络流量数据的非平稳特性而被广泛采用。

前期研究的网络流量ARIMA模型的被分析数据大多采用小范围的局域网，且预测结果的数据点较少，其分析结果不具有代表性。因此本文被分析数据采用贝尔实验室提供的BC-Oct89Ext实测流量数据，流量数据是在贝尔Morristown研究中检测的以太网数据，包含一百万个数据包，数据具有充分的代表性。本文采用ARIMA（0，2，2）模型对BC-Oct89Ext实测流量数据进行建模并对流量数据进行了48个数据点的预测。根据分析结果，ARIMA模型可以有效描述部分非平稳网络流量数据，且预测结果与真实流量数据十分接近，建模结果和预测方法可以广泛应用于网络流量监控、网络资源优化和网络拥塞避免研究。

1 ARIMA模型介绍

ARIMA模型[5]全称为自回归积分滑动平均模型(Autoregressive Integrated Moving Average Model），是由Box和Jenkins于70年代初提出的著名时间序列预测方法，所以又称为box-jenkins模型。ARIMA（p，d，q）模型中p为自回归阶数，q为移动平均阶数，d为是序列平稳时所做的差分次数。模型的表达式为：

其中，B为滞后算子：

ARIMA模型是基于有限次差分后为稳定的时间序列，AR、MA、ARMA模型可以看成是ARIMA的某种特殊形式。

2 网络流量建模及预测分析

2.1 网络流量数据介绍

本研究选取贝尔实验室提供的BC-Oct89Ext实测流量数据。流量数据是在贝尔Morristown研究中检测的以太网数据，包含一百万个数据包。本文选取了BC-Oct89Ext流量数据的部分数据段进行建模分析。图1给出了BC-Oct89Ext实测流量数据中的10 000个数据包，流量数据额持续时间为1 752.26 s。

2.2 ARIMA建模及预测流程

ARIMA建模首先需要判断被分析数据的平稳性，对于非平稳序列采取差分运算去掉其趋势或周期性，然后确定数据的自回归参数p和滑动平均参数q，得到数据的ARIMA模型，具体的建模及预测流程为：

（1）采用Dickey-Fuller Test方法检测被分析数据的平稳性；

（2）如果被分析数据是非平稳序列，则要先进行d阶差分运算，将其转化为平稳序列；

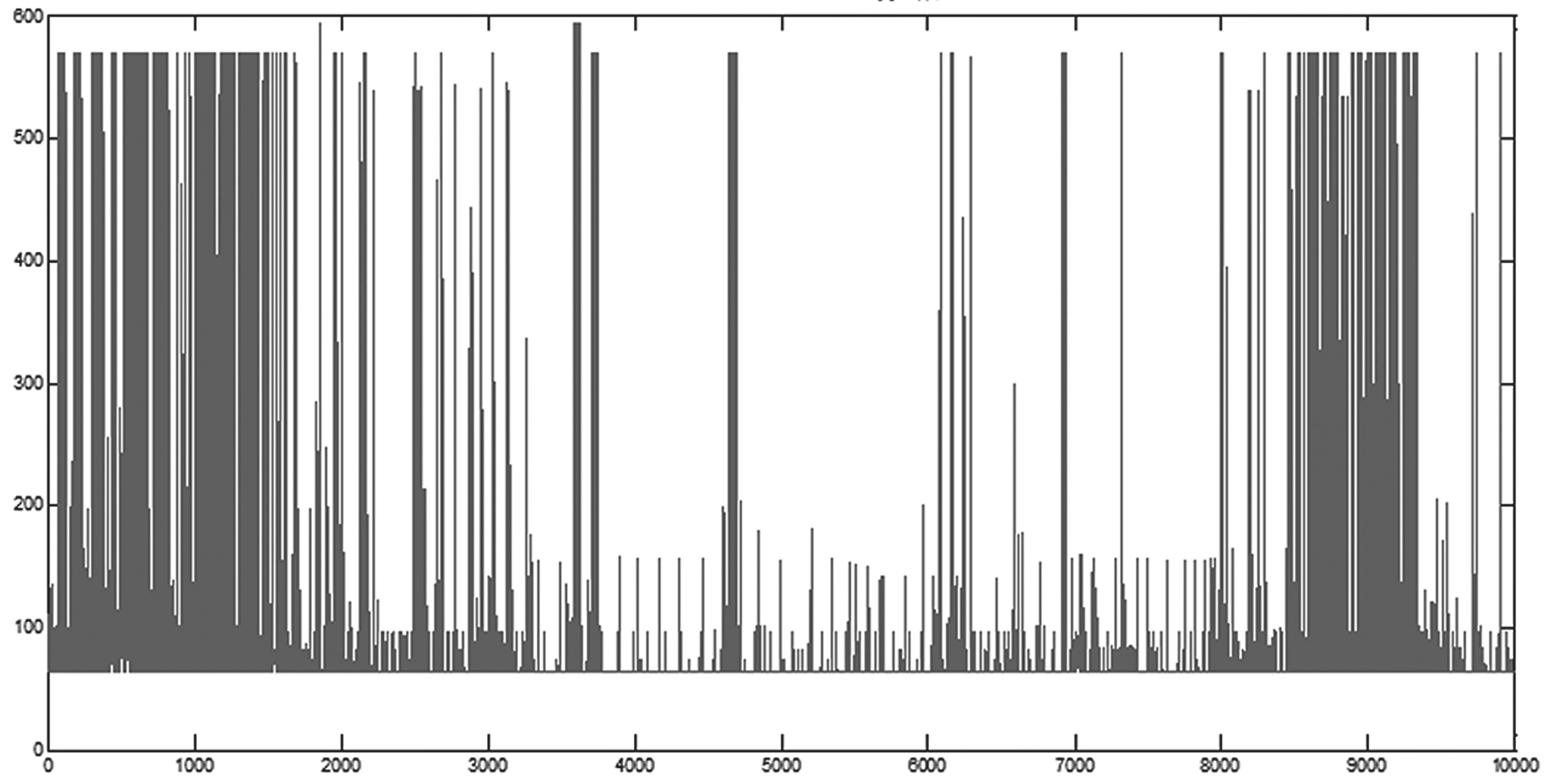
图1 BC-Oct89Ext流量数据

（3）对d阶差分后的平稳时间序列分别求得其自相关系数ACF（Auto Correlation Function）和偏自相关系数PACF（Partial Autocorrelation Coefficient Pacf），通过对自相关图和偏自相关图的分析，得到最佳的阶数p和阶数q；

（4）根据分析得到的参数d，p和q建立ARIMA模型，并对模型进行模型检验；

（5）利用已通过检验的模型进行预测分析。

ARIMA的建模及预测流程如图2所示。

图2 ARIMA建模流程

2.3 ARIMA模型参数估计

本研究对图1所示部分BC-Oct89Ext流量数据建立ARIMA模型。根据2.2节给出的建模流程，首先应用Augment Dickey-Fuller test（ADF）方法检测数据的平稳性，如果数据为非平稳则对数据进行差分，根据差分次数确定模型参数d的数值，根据分析d=2。

为了估计参数p和q的数值，首先对得到的平稳时间序列分别求得其自相关系数ACF和偏自相关系数PACF。图3给出网络流量数据差分后的ACF的前40个数据点，ACF明显具有截尾性。图4给出差分后数据的PACF的前12个数据点，从图中可以看出报头捕获数据块（Preamble Acquisition Chunk，PAC）具有拖尾性。根据BC-Oct89Ext流量差分数据的ACF和PACF可以推断出数据可以用滑动平均模型（Moving Average Model，MA模型）描述，且可以初步判断出差分后数据模型参数p=0，q=2。

图3 差分序列自相关函数

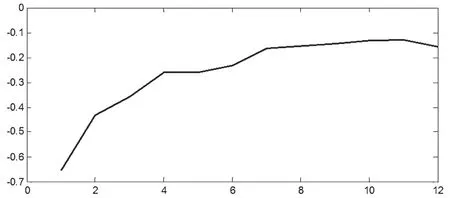
图4 差分序列偏相关函数

2.4 ARIMA模型检验

按照以上参数估计结果可以初步建立模型为ARIMA(0，2，2)。为了验证模型参数的有效性，本研究采用最小二乘法估计法计算10阶以内的AIC（Akaike Information Criterion）信息准则的数值，结果如表1所示。应用AIC准则为模型定阶，取AIC值为最小值的阶次，由上表可知阶次为2时，AIC值为11 091.480 7，符合最小条件，因此判断模型阶次为2。

表1 ARIMA（0，2，2）模型AIC值

根据已经建好的ARIMA（0，2，2）模型，得到样本逼近曲线如图5所示，其中“*”为模型逼近曲线数据点。从图5中可以看出样本逼近曲线与BC-Oct89Ext网络流量数据基本吻合，证明了模型的正确性。

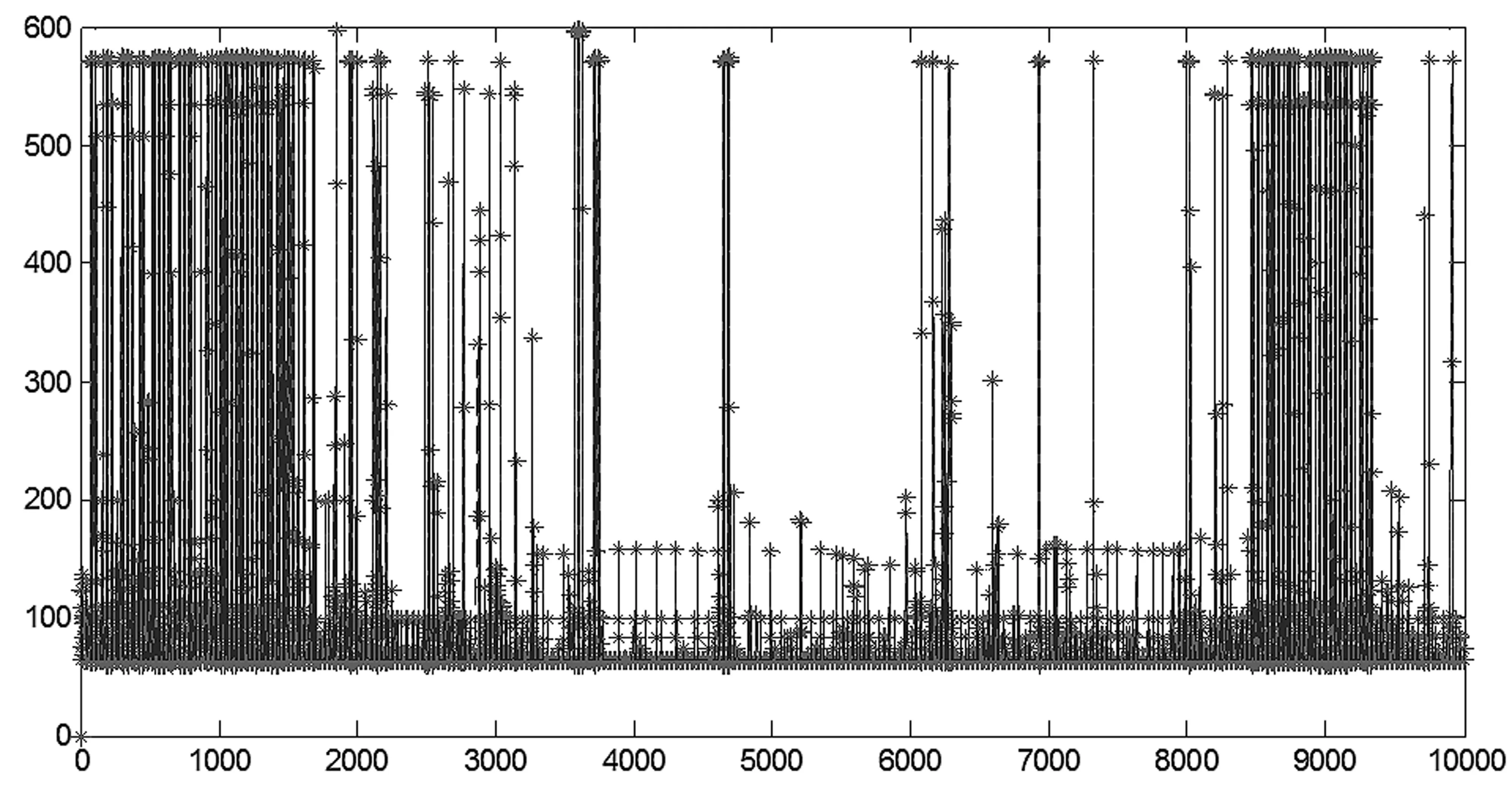
图5 模型样本逼近预测曲线

最后，对残差序列进行分析检验，残差序列符合白噪声序列的特性，其自相关系数为-0.110 6。经过AIC信息准则测试，样本逼近曲线和残差序列分析，本研究建立的ARIMA（0，2，2）模型可以准备描述BC-Oct89Ext网络流量数据。

2.5 网络流量ARIMA模型预测

本研究选取图1给出的BC-Oct89Ext实测流量数据中最后48个数据点进行预测。应用2.4节验证的ARIMA（0，2，2）模型对BC-Oct89Ext流量数据进行预测分析。图6给出了BC-Oct89Ext流量数据最后48个数据点的预测结果，其中“+”号为实际的流量数据，“*”号为ARIMA（0，2，2）模型的预测结果。从图6可以看出，预测结果与真实的流量数据十分接近，证明模型的可靠性。为了量化分析预测效果，对预测平均绝对误差进行了计算，48个数据点的预测平均绝对误差为5.171 4，预测误差较小可以对网络流量的趋势进行有效预测。

图6 ARIMA模型48步预测结果

3 结 语

本文对贝尔实验室提供的BC-Oct89Ext实测流量数据进行分析并建立ARIMA（0，2，2）模型，应用ARIMA模型实现网络流量数据预测。实验结果表明ARIMA模型可以较好描述实际网络流量数据并可用于实际网络流量预测。ARIMA模型对于有限次差分后平稳的非平稳网络数据建模效果好，且预测误差较小。本文研究结果可以应用于网络资源优化和网络拥塞避免，对网络业务规划、故障检测、资源调配等操作也具有一定借鉴意义。在后续研究中将对具有自相似特性的网络流量数据进行建模研究，建立更加稳定可靠的数学模型。