考虑非傅立叶效应的固液相变分子动力学模拟
2019-04-29牛泽伟
关 阳, 李 凌, 牛泽伟
(上海理工大学,能源与动力工程学院,上海 200093)
1 引 言
飞秒激光自开始用于材料加工以来,凭借其独特的优势成为微细加工的理想工具,并被广泛应用于不同的领域[1-4].飞秒激光与材料相互作用的中间过程对结果影响很大,尤其是加工的材料越来越小,加工时间也越来越短,所以研究加工过程中的传热机理有着重要意义. 目前对飞秒激光和金属材料的相互作用机理已有大量的研究,很多都是采用连续介质模型,使用最广泛的是基于傅立叶定律的抛物线两步加热模型[5-7].连续介质模型的缺点是无法获得激光与材料相互作用过程的微观特性.分子动力学方法是一种原子尺度的数值模拟方法,可以从微观角度对材料的相变过程进行直观描述.但经典的分子动力学方法不能描述激光与材料作用时电子晶格间的非平衡传热过程.并且在处理飞秒激光加工材料的过程中,由于激光脉宽接近或小于电子和晶格的弛豫时间,需要考虑非傅里叶效应,尤其是发生快速的相变过程时.
因此,为了兼顾连续介质模型与分子动力学方法的优点,本文分别将基于傅立叶定律的抛物线模型(parabolic model)和考虑非傅立叶效应的双曲线模型(hyperbolic model)与分子动力学方法相结合来研究飞秒激光照射金箔过程中发生的固液相变现象,并对得到的结果进行对比分析,从而获取了固液界面的变化规律,随后采用考虑非傅立叶效应的模型探讨了激光能量密度和脉冲宽度对相变过程的影响.
2 物理模型和数学方法
2.1 物理模型
激光照射金箔的物理模型如图1所示.脉宽tp=200 fs、能量密度J=50 J/m2的激光从上边均匀照射金箔,激光的作用时间为800 fs.金箔厚度L=12.24 nm,初始温度为300 K,电子和晶格的弛豫时间分别是40 fs和800 fs[8].根据文献[9],当模拟的原子数超过500时,即具有统计学意义,本文计算的模型共包含1089个原子.金的势函数采用嵌入原子(EAM)势函数[10].长(x)、宽(y)方向均采用周期性边界条件,金箔下表面设为弹性表面[11],上表面设为自由表面.
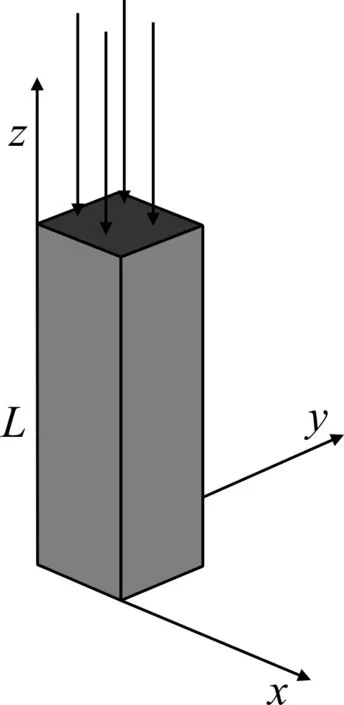
图1 物理模型Fig. 1 Physical model
2.2 耦合双温度模型的分子动力学模拟
基于傅立叶定律的抛物线模型下电子等效热传导方程为[12]:
(1)
非傅立叶效应下考虑电子和晶格弛豫效应的影响,双曲线模型中电子等效热传导方程为[8]:
(2)
式中Ce为电子热容[13],t为时间,T为温度,τ为弛豫时间,下脚标e和l分别代表电子和晶格,ke为等效电子导热系数[14],G为电子-晶格的耦合因子[15],S为源项[12].
由于金箔中电子的热熔比晶格的热熔小,当激光作用金箔时,电子温度在短时间内急剧升高,而此时晶格温度的变化很小,所以忽略激光与晶格的直接作用.与此同时,电子声子的耦合作用使金箔内原子产生了附加运动,随着电子温度的不断升高原子运动逐渐加剧,随即通过统计原子的运动状态从微观角度描述晶格系统.
加入激光后原子的受力方程为[16]:
(3)
式中Fi为第i个原子在激光作用前所受的力,mi为第i个原子的质量,ri(x,y,z,t)为某时刻原子所在位置,t为时间,viT为原子的运动速度vi与该原子所在层的运动速度vc的差值.ξ为修正系数,其计算公式为[17]:
(4)
n=ΔtMD/ΔtTTM,ΔtMD为分子动力学模型中的时间步长,ΔtTTM为双温度模型中的时间步长;Tl为每一个晶格的平均温度,计算公式为:
(5)
式中KB为玻尔兹曼常数,Ncell为每一个晶格中的原子个数.
2.3 固液状态的判定
根据文献[17]中的序参数法来判定原子的固液状态,每一个原子的序参数为:
(6)
式中两原子i和j之间的距离rij=|rij|,且rij小于截断半径rcut;h为原子i截断半径内的原子总数;q为一组倒易矢量[16].
在截断半径内,与每个原子邻近的h个原子的序参数的平均值为:
(7)
根据文献[10],当序参数在[0,0.04]时,原子为液态;当序参数在[0.04,1]时,原子为固态.序参数的平均值越大,原子越有序,对于理想晶格,原子的序参数为1;而对于液态物质,原子的序参数接近0.
3 结果与讨论
3.1 算法的验证
为了对算法进行验证,采用耦合了两种双温度模型的分子动力学方法对脉宽tp=200 fs、能量密度J=5 J/m2的激光照射12.24 nm厚金箔的传热过程进行模拟研究,模型初始温度T1=250 K.
两种模型中电子和晶格温度均在12 ps左右达到平衡,在不考虑非傅立叶效应时,达到温度平衡后金箔的温度T2=313 K;考虑非傅立叶效应时,达到温度平衡后金箔温度T3=320 K.
金箔在整个过程中吸收的能量:
Q=(1-R)·J·S=(1-0.6)×
5×(3×4.08×10-10)2=2.996×10-18J
(8)
式中R为金箔表面的反射率[16],S为激光照射到金箔的面积.
能量守恒方程为[18]:
Q=cp·m·ΔT
(9)
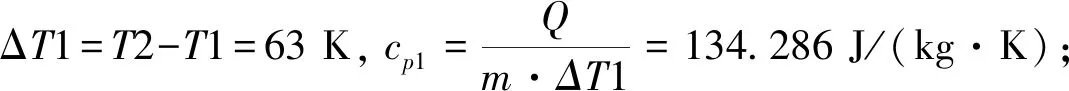

3.2 抛物线模型和双曲线模型的结果对比
论文进而分别采用耦合了抛物线模型和双曲线模型的分子动力学方法对脉宽为200 fs、能量密度为50 J/m2的激光照射12.24 nm厚金箔的固液相变过程进行了模拟研究.
图2为两种模型中金箔原子在60 ps时的平均序参数分布图.当平均序参数在[0,0.04]时,金箔为液态;平均序参数在[0.04,1]之间时,金箔为固态.图2(a)是抛物线模型的平均序参数分布图,从图中可以看出当0≤z≤105×10-10m时,金箔为固态;当105×10-10m≤z≤131×10-10m时,金箔为液态.图2(b)是双曲线模型的平均序参数分布图,从图中可以看出当0≤z≤71×10-10m时,金箔为固态;当71×10-10m≤z≤131×10-10m时,金箔为液态.在60 ps时,双曲线模型的熔化深度大于抛物线模型.
图3(a)给出了两种模型下金箔固液界面位置随时间的变化情况,可以看出熔化初始阶段固液界面下降明显,然后熔化速度减慢,而后熔化速度又再次加快,直到金箔完全熔化.金箔熔化速度的改变是由于金箔中心生成了激光引发的压力[19],该压力向上下两个表面传播,中心压力高并逐渐向两侧减小,从而引起了熔化速度的变化.图3(b)所示为固液界面温度随时间的变化情况,初始阶段,界面温度随时间增加而升高,而后又逐渐降低.这是由于模拟中激光脉冲的时间只有800 fs,激光先将能量迅速传递给金箔表面的电子,而后金箔表面的电子以缓慢的速度将能量传递给金箔表面的晶格,直至晶格温度升高并达到熔点从而开始熔化.在这个过程中,晶格中的能量不断向金箔深处传递,于是固液界面温度呈现出先升高达到峰值后再下降的趋势.

图2 两种模型中金箔原子的平均序参数随金箔厚度的分布情况Fig. 2 Distribution of average order parameter versus gold thickness in two models
从图3中还可以看出在同一时刻,双曲线模型的熔化深度和界面温度明显大于抛物线模型.双曲线模型下金箔在10 ps时开始熔化,在18 ps时固液界面温度达到最高值1200 K;抛物线模型下金箔在19 ps时开始熔化,在21 ps时固液界面温度达到最高值1153 K.在110 ps时,双曲线模型下的金箔完全熔化;在250 ps时,抛物线模型下的金箔仍未完全熔化.造成这一结果的原因是(2)式中的最后一项,把S-G(Te-Tl)看成S’,
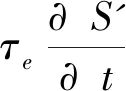
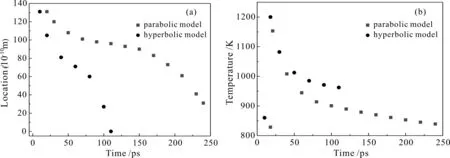
图3 两种模型下金箔固液界面位置(a)和温度(b)随时间的变化情况Fig. 3 Solid-liquid interface (a)location and (b)temperature versus time in two models
3.3 非傅立叶效应下的相变传热研究
在非傅立叶效应下对脉宽为200 fs、能量密度为50 J/m2的激光照射12.24 nm厚金箔的固液相变过程进行了模拟研究,图4为120 ps内金箔中电子和晶格的平均温度随时间的变化情况.从图中可以看出当激光作用于金箔后,金箔内的电子温度急剧升高并达到最大值,然后随时间逐渐降低;晶格温度首先随时间缓慢增加,当金箔在27 ps左右达到温度平衡后晶格温度产生随时间产生周期性波动.
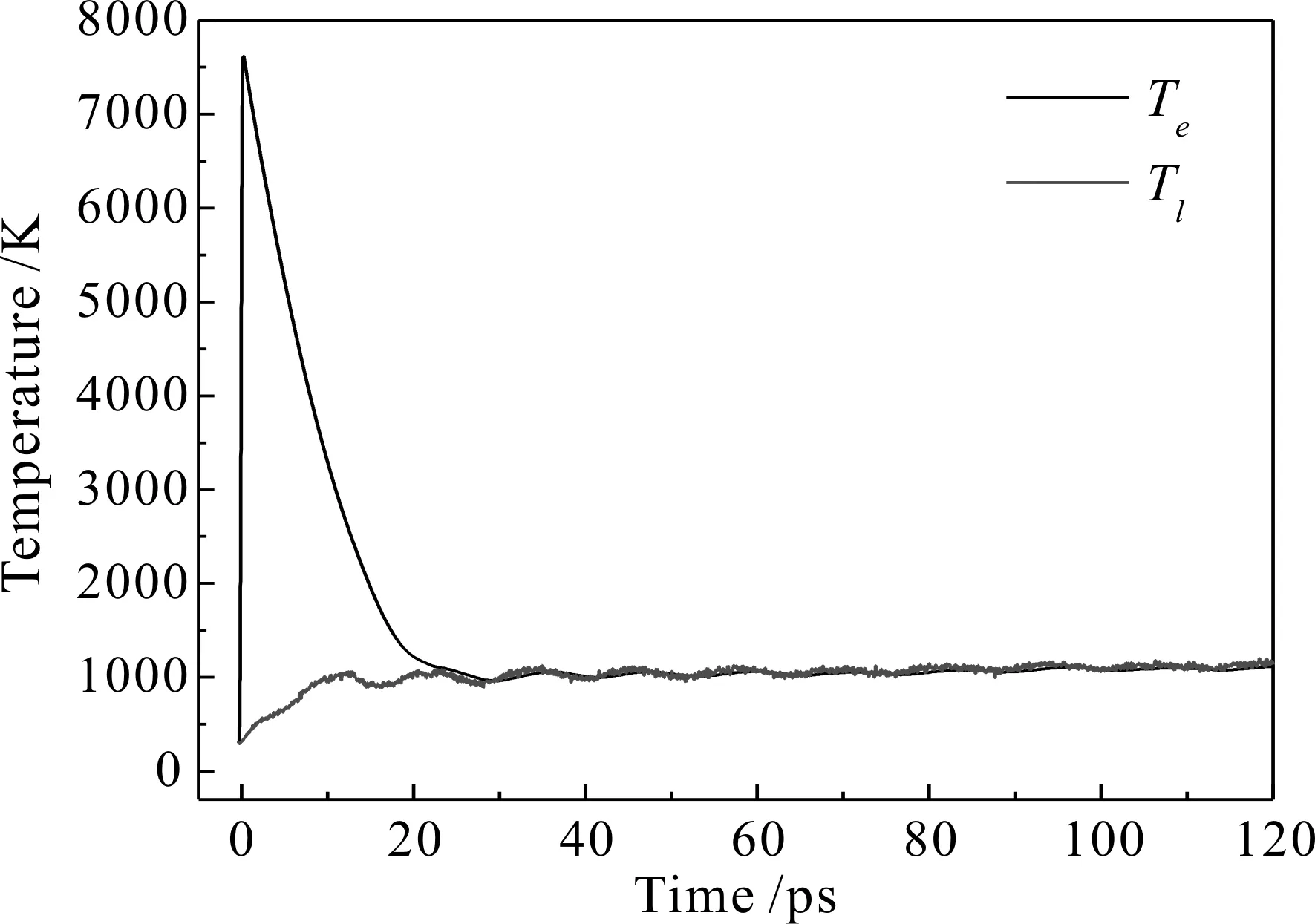
图4 金箔中电子和晶格的平均温度随时间的变化情况Fig. 4 Average temperature of electrons and lattices in gold foil versus time
不同时刻金箔原子的微观排列如图5所示.从图中可以看出,原子在初始平衡状态下排列比较规则,在各自的原胞内小范围振动.随着激光能量的加入,金箔的温度逐渐升高,同时上层原子的晶格结构最先遭到破坏,原子排列逐渐变得不规则,金箔开始熔化.随着时间推移,这种不规则排列开始向金箔底部扩散,固液界面也随之向金箔底部移动,最终在110 ps时,金箔全部熔化.
论文进而研究了非傅立叶效应下激光参数对金箔熔化过程的影响.图6(a)所示为在非傅立叶效应下,不同的激光能量密度下金箔固液界面位置随时间的变化情况.由图可知,当激光能量密度较小(30 J/m2)时,金箔只有表面很浅一层发生熔化,其他部分未发生熔化,随着激光能量密度的不断增大,晶格系统吸收的热量也不断增加,从而金箔的熔化深度不断加大,熔化速度也逐渐加快,当激光能量密度J=50 J/m2时,金箔在110 ps全部熔化.在同一时刻,能量密度越大,熔化深度越大.图6(b)所示为不同能量密度下金箔固液界面温度随时间的变化情况.在同一时刻,激光能量密度越大,金箔中晶格系统吸收的热量就越多,界面温度达到的峰值也越高,并且达到峰值所需的时间也越短.
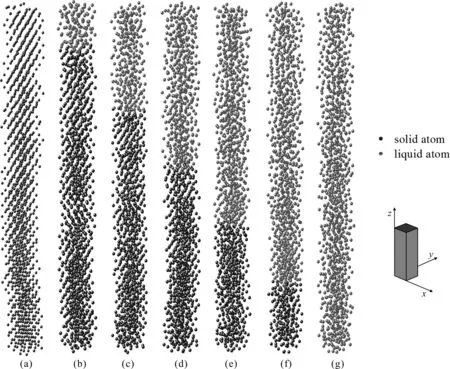
图5 不同时刻金箔原子的微观排列图 (a)t=0 ps(b)t=20 ps(c)t=40 ps(d)t=60 ps(e)t=80 ps(f)t=100 ps(g)t=110 psFig. 5 Microscopic projections of gold foil at different moments (a)t=0 ps(b)t=20 ps(c)t=40 ps(d)t=60 ps(e)t=80 ps(f)t=100 ps(g)t=110 ps

图6 不同能量密度下金箔固液界面位置(a)和温度(b)随时间的变化情况Fig. 6 (a)Location and (b)temperature of solid-liquid interface versus time at different laser flux densities
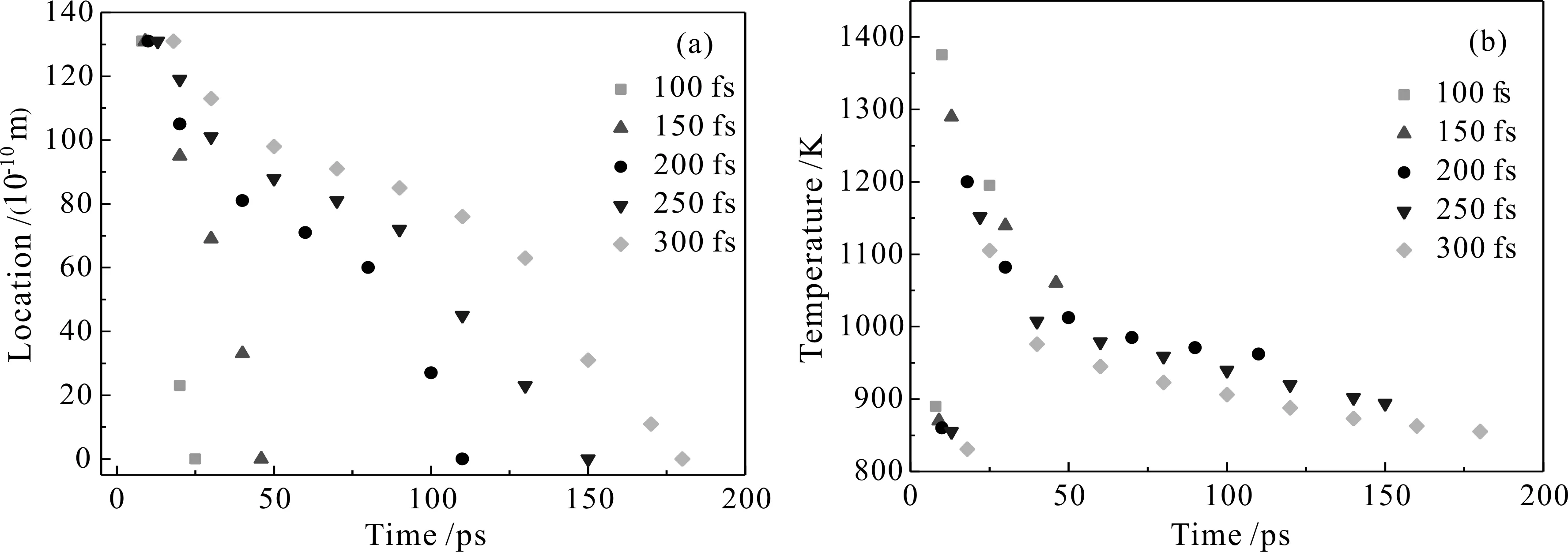
图7 不同脉冲宽度下金箔固液界面位置(a)和温度(b)随时间的变化情况Fig. 7 (a)Location and (b)temperature of solid-liquid interface versus time at different laser pulse widths
激光的脉冲宽度也是影响激光烧结过程的一个重要因素.图7所示为不同脉宽下金箔固液界面位置和温度随时间的变化情况.在同一时刻,随着脉宽的增大,金箔熔化深度越小,总的熔化时间越长,而界面温度也越小.
4 结 论
本文利用耦合双温度模型的分子动力学方法从微观角度对飞秒激光照射金箔的固液相变过程进行了模拟研究,在本文研究的参数范围内获得以下结论:
(1)当飞秒激光照射金箔时,金箔的晶格结构随着温度的升高逐步遭到破坏,金箔开始熔化,固液界面随时间逐渐向金箔底部移动,界面温度随能量在金箔中的传递先升高后降低.
(2)在相同条件下,考虑非傅立叶效应时,金箔熔化的时间较早,并且固液界面温度和熔化深度比不考虑非傅里叶模型的计算结果大.
(3)较大的激光能量密度和较小的激光脉冲宽度会导致较高的固液界面温度和较大的熔化深度,且熔化时间较短.
